Grupo - Tráfego

Integrantes: Rodrigo Zamin Ferreira (262692) e Maurício Gomes de Queiroz (264889)

Introdução

O estudo de caso do comportamento do tráfego urbano se mostra de grande utilidade nos dias atuais, onde metrópoles apresentam grandes volumes de veículos se deslocando pela cidade. Em horários de pico, por exemplo, às 18h, Porto Alegre apresenta média de lentidão de 83km, enquanto São Paulo chega a incríveis 485km.

A modelagem de tal comportamento permite um estudo das regras básicas que motoristas tendem a seguir em situações reais, levando assim a um melhor entendimento da formação e desenvolvimento de congestionamentos.

Aqui é proposto um modelo simples do funcionamento normal de uma avenida utilizando autômatos celulares, inicialmente com apenas uma faixa, sendo após estendido para n faixas e então, simulado um cruzamento.

Autômatos Celulares

Weimar define um autômato celular em "Simulation with Cellular Automata", informalmente, como um vetor de células sendo caracterizado pelas seguintes propriedades básicas:

• A evolução se dá em passos discretos de tempo;

• Cada célula é caracterizada por um estado pertencente a um conjunto finito de estados;

• Cada célula evolui de acordo com as mesmas regras que dependem somente do estado em que a célula se encontra e de um número finito de vizinhos;

• A relação com a vizinhança é local e uniforme.

Apesar de simples, autômatos celulares (AC) são capazes de simular sistemas dinâmicos complexos e são extensivamente utilizados aqui, onde cada célula representa uma posição na avenida, que pode conter um veículo ou não. Caso contenha um veículo, a célula possui um estado associado a si que representa sua velocidade, que pode assumir valores discretos de 0 a um valor máximo, que aqui é definido como 5; caso contrário, a célula possui um estado que indica que está vazia, sendo utilizado o estado -1 para esse objetivo.

A atualização dos estados é feita de forma não-síncrona (os estados das células são atualizados um após o outro) e homogênea (as regras de atualização não dependem da posição espacial da própria célula, somente da posição relativa dos vizinhos).

A mudança dos estados é feita com base em regras que se baseiam nos estados da vizinhança, tendo também algumas mudanças estocásticas, caracterizando um método de Monte Carlo.

Regras de Aceleração

Estabelecemos as regras de mudança da velocidade com base no artigo de Nagel e Schreckenberg (1992). São três os casos em que um autômato do modelo descrito aqui muda de velocidade:

Regra 1: A velocidade é reduzida caso a distância entre um carro e o veículo que vai à sua frente seja suficientemente pequena para que haja colisão durante a atualização de posições da simulação.

Regra 2: De modo análogo, aumenta-se a velocidade caso a velocidade atual for menor que a máxima e seja suficientemente grande para que não haja colisão durante a atualização de posições da simulação usando a velocidade nova.

Regra 3: É também introduzido no modelo um fator que aleatoriamente reduz a velocidade do veículo, para que seja levado em conta flutuações da velocidade devido ao comportamento humano. Esse passo é essencial, já que sem ele o modelo seria determinístico.

Ou seja, sendo $dist$ a distância entre um carro e o que está à sua frente, e $v$ a velocidade do carro,

Regra 1: Caso $dist\leq v$, então $v\rightarrow dist-1$

Regra 2: Caso $dist>v+1$, então $v\rightarrow v+1$

Regra 3: Com uma probabilidade $p$, $v\rightarrow v-1$

Faixa Única

Gráfico 1: 1 Carro em faixa única

O problema de faixa única, mesmo que simples, gera discussões muito boas quando simulado. O cenário consiste em uma avenida de uma faixa, com $L$ células, com carros que se movem da esquerda para a direita, submetidos às regras citadas anteriormente. Além disso, foram utilizadas condições de contorno periódicas, e os carros foram inicializados em posições equidistantes. Os valores dos parâmetros utilizados foram $L=15$ e $v_{max}=3$.

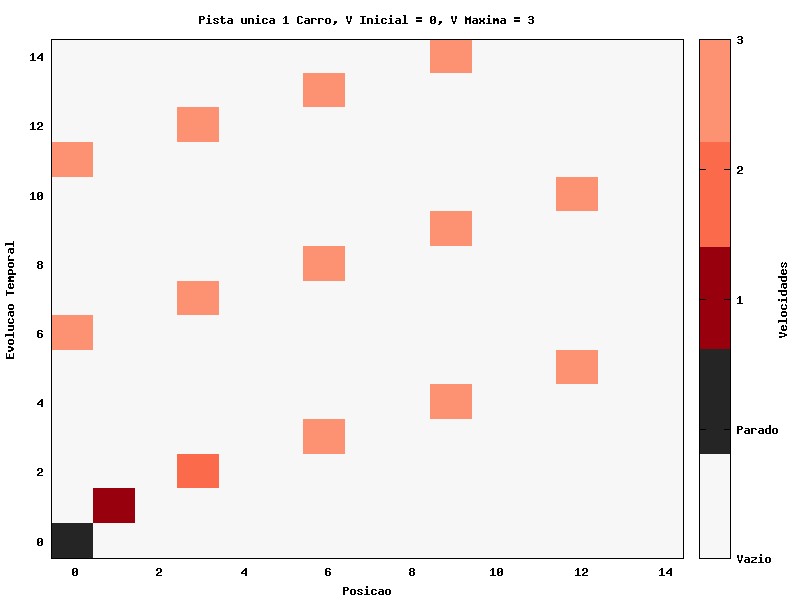
Uma primeira abordagem, com finalidade situar a simulação, é com um único carro, sem implementação da redução de velocidade randômica.

No gráfico ao lado, o carro se desloca, partindo do repouso e com aceleração, até atingir a velocidade máxima, com valor 3, que é mantida no decorrer do tempo. Tal gráfico mostra o funcionamento base dos autômatos e da visualização da evolução temporal dos mesmos.

Gráfico 2: 7 Carros em faixa única

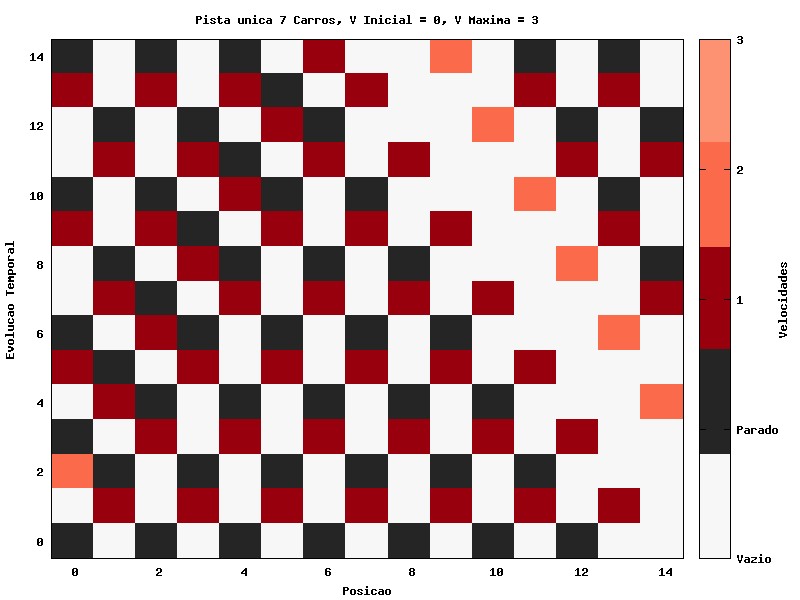
O próximo passo é estendermos o modelo para o caso com 7 carros, isto é, uma densidade de quase 0.5 carros/célula. Há uma tendência natural do surgimento de trechos de lentidão, e trechos onde a pista está livre. Esses trechos se propagam, de acordo com a simulação, contra o sentido de movimentação dos carros.

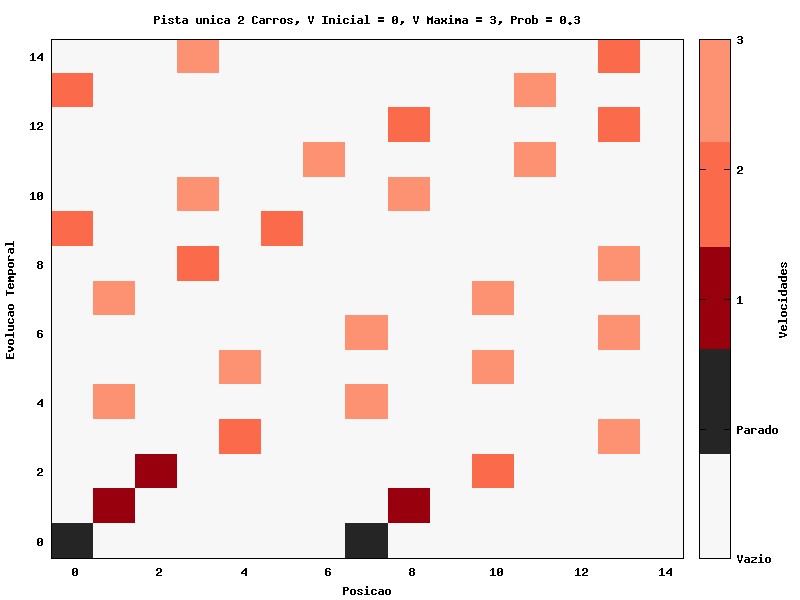
Agora, podemos introduzir a probabilidade de redução de velocidade, em uma situação com dois carros. Percebe-se, por exemplo, no gráfico 3, que o carro iniciado na posição 0 permanece dois passos de tempo com velocidade 1, enquanto o segundo carro já havia mudado de velocidade. Nestes gráficos ainda não há redução de velocidade devido à densidade baixa, mas ao decorrer do tempo, os carros oscilam sua velocidade entre 3 e 2.

Gráfico 3: 2 Carros em faixa única, com probabilidade de redução

Ao aplicarmos a simulação para 5 carros, observamos que já há pontos de lentidão, causados pela probabilidade de redução da velocidade.

Gráfico 4: 5 Carros em faixa única, com probabilidade de redução

Bibliografia

https://www.ppgee.ufmg.br/defesas/113M.PDF