Equação de Dirac
Grupo: André Luis Della Valentina, Lucas dos Santos Assmann, Vinícius Bayne Müller
Introdução
A equação de Dirac descreve uma partícula relativística de spin , como o elétron, com estrutura análoga a da equação de Schrödinger. Ela surgiu inicialmente como tentativa de explicar discrepâncias entre experimentos e teoria para o espectro do átomo de hidrogênio, possibilitando correções para o cálculo da energia do elétron em diferentes níveis (as chamadas correções de estrutura fina). Além disso, por meio dela foi possível prever a existência de antimatéria: descrevendo o elétron, ela também descreve o pósitron.
A fim de compatibilizar a Mecânica Quântica com a Relatividade Especial, a equação diferencial parcial é de primeira ordem tanto no tempo quanto no espaço (diferentemente da equação de Schrödinger, que é de segunda ordem no espaço). A equação de Dirac pode ser escrita de diversas formas; aqui, apresentamo-la explicitamente como um sistema de EDPs acopladas, mais conveniente para os propósitos do trabalho.
Assim como a equação de Schrödinger, a construção da equação de Dirac vem a partir do operador Hamiltoniano, que descreve a evolução temporal do estado quântico em questão:
onde, como anteriormente, os autovalores de correspondem aos valores possíveis de energia que o sistema pode assumir.
A mudança com relação à Mecânica Quântica não relativística acontece quando consideramos a energia relativística da partícula:
Assim, o Hamiltoniano é modificado para representar a medida da energia relativística total.
Diferentemente da equação de Schrödinger, aqui não representa apenas uma função de onda, mas sim um conjunto de quatro delas. Usando a notação
,
as componentes de representam as funções de onda associadas ao elétron e ao pósitron: (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_2} ) representa a função de onda do elétron com spin up (down), e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_3} (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_4} ) representa a função de onda do pósitron com spin up (down). O objeto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(\boldsymbol{x},t)} é chamado de spinor.
Dedução da equação de Dirac em uma e duas dimensões
Consideraremos neste trabalho a equação de Dirac em uma e duas dimensões, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} . A escolha dessas coordenadas se dá pela conveniência do acoplamento das EDPs: nesse caso, as quatro equações acopladas passam a ser acopladas duas a duas, facilitando o estudo do sistema.
Construção do Hamiltoniano completo
Consideremos uma partícula sob ação de um potencial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(\boldsymbol{x};t)} (onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{x} = (x, y, z)^{T}} ), que afeta a energia potencial da partícula, e de um potencial "escalar" Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{sc}(\boldsymbol{x};t)} , que afeta a massa de repouso da mesma. Seguindo uma das propostas possíveis para o Hamiltoniano, temos
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = c \boldsymbol{\alpha} \cdot \boldsymbol{p} + \beta(mc^2 + V_{sc}) + VI_4 }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\alpha} = \alpha_x \hat{i} + \alpha_y \hat{j} + \alpha_z \hat{k}} ; Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_i} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} são matrizes 4x4 adimensionais e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{p}} é o vetor momento linear da partícula.
Pode-se mostrar que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\alpha}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} devem satisfazer certos vínculos, limitando as escolhas possíveis para essas matrizes. A escolha mais simples e usualmente adotada consiste em tomar
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = \begin{pmatrix} I_2 & 0 \\ 0 & -I_2 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_x = \begin{pmatrix} 0 & \sigma_x \\ \sigma_x & 0 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{pmatrix} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_y = \begin{pmatrix} 0 & \sigma_y \\ \sigma_y & 0 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 & -i \\ 0 & 0 & i & 0 \\ 0 & -i & 0 & 0 \\ i & 0 & 0 & 0 \end{pmatrix} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_z = \begin{pmatrix} 0 & \sigma_z \\ \sigma_z & 0 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \\ 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \end{pmatrix} }
Sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{p} = -i\hbar\nabla} , podemos escrever o produto escalar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\alpha} \cdot \boldsymbol{p}} como
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\alpha} \cdot \boldsymbol{p} = -i\hbar\left(\alpha_x \frac{\partial}{\partial x} + \alpha_y \frac{\partial}{\partial y} + \alpha_z \frac{\partial}{\partial z}\right)}
Portanto, em notação matricial o Hamiltoniano Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} pode ser escrito como
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = -i \hbar c \begin{pmatrix} 0 & 0 & \frac{\partial}{\partial z} & \frac{\partial}{\partial x} - i\frac{\partial}{\partial y} \\ 0 & 0 & \frac{\partial}{\partial x} + i\frac{\partial}{\partial y} & -\frac{\partial}{\partial z} \\ \frac{\partial}{\partial z} & \frac{\partial}{\partial x} - i\frac{\partial}{\partial y} & 0 & 0 \\ \frac{\partial}{\partial x} + i\frac{\partial}{\partial y} & -\frac{\partial}{\partial z} & 0 & 0 \\ \end{pmatrix} + \begin{pmatrix} V + mc^2 + V_{sc} & 0 & 0 & 0 \\ 0 & V + mc^2 + V_{sc} & 0 & 0 \\ 0 & 0 & V - mc^2 - V_{sc} & 0 \\ 0 & 0 & 0 & V - mc^2 - V_{sc} \\ \end{pmatrix} } Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = \begin{pmatrix} V + mc^2 + V_{sc} & 0 & -i\hbar c\frac{\partial}{\partial z} & -i\hbar c\frac{\partial}{\partial x} - \hbar c\frac{\partial}{\partial y} \\ 0 & V + mc^2 + V_{sc} & -i\hbar c\frac{\partial}{\partial x} + \hbar c\frac{\partial}{\partial y} & i\hbar c\frac{\partial}{\partial z} \\ -i\hbar c\frac{\partial}{\partial z} & -i\hbar c\frac{\partial}{\partial x} - \hbar c\frac{\partial}{\partial y} & V - mc^2 - V_{sc} & 0 \\ -i\hbar c\frac{\partial}{\partial x} + \hbar c\frac{\partial}{\partial y} & i\hbar c\frac{\partial}{\partial z} & 0 & V - mc^2 - V_{sc} \\ \end{pmatrix} }
Unidades naturais e redução para duas dimensões
A fim de simplificar o formalismo, adotamos as chamadas "unidades naturais", onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar = c = m = 1 } . Note que isso equivale a reescalar as quantidades físicas do problema por um fator adequado. Ao fazer Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle c=1} , também assumimos que a partícula está no limite relativístico.
Além disso, queremos estudar o problema em duas dimensões. Observamos que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi(x,y,z) = \Psi(x,y)} ; logo, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial \Psi}{\partial z} = 0} . Portanto, temos o Hamiltoniano simplificado
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = \begin{pmatrix} V + 1+ V_{sc} & 0 & 0 & -i\frac{\partial}{\partial x} - \frac{\partial}{\partial y} \\ 0 & V + 1 + V_{sc} & -i\frac{\partial}{\partial x} + \frac{\partial}{\partial y} & 0 \\ 0 & -i\frac{\partial}{\partial x} - \frac{\partial}{\partial y} & V - 1 - V_{sc} & 0 \\ -i\frac{\partial}{\partial x} + \frac{\partial}{\partial y} & 0 & 0 & V - 1 - V_{sc} \\ \end{pmatrix} }
Forma explícita final
Retornando ao problema original, queremos resolver
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar \frac{\partial}{\partial t} \Psi = H\Psi \to \left[iI_4\frac{\partial}{\partial t} - H\right]\Psi = 0 }
Novamente utilizando a notação matricial, obtemos
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} i \frac{\partial}{\partial t} - V - V_{sc} - 1 & 0 & 0 & i \frac{\partial}{\partial x} + \frac{\partial}{\partial y} \\ 0 & i \frac{\partial}{\partial t} - V - V_{sc} - 1 & i \frac{\partial}{\partial x} - \frac{\partial}{\partial y} & 0 \\ 0 & i \frac{\partial}{\partial x} + \frac{\partial}{\partial y} & i \frac{\partial}{\partial t} - V + V_{sc} + 1 & 0 \\ i \frac{\partial}{\partial x} - \frac{\partial}{\partial y} & 0 & 0 & i \frac{\partial}{\partial t} - V + V_{sc} + 1 \end{pmatrix} \begin{pmatrix} \Phi_1 \\ \Phi_2 \\ \Phi_3 \\ \Phi_4 \end{pmatrix} = 0 }
Realizando a multiplicação matricial, pode-se ver que se obtém dois sistemas acoplados: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_1} com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_4} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_2} com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_3} . Escolhendo o sistema de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_1} com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_4} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \left(i \dfrac{\partial}{\partial t} - V - V_{sc} - 1\right) \Phi_1 + \left(i \dfrac{\partial}{\partial x} + \dfrac{\partial}{\partial y}\right) \Phi_4 = 0 \\ \left(i \dfrac{\partial}{\partial x} - \dfrac{\partial}{\partial y}\right) \Phi_1 + \left(i \dfrac{\partial}{\partial t} - V + V_{sc} + 1\right) \Phi_4 = 0 \end{cases} }
Simplificando e isolando a derivada temporal, obtemos por fim
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \dfrac{\partial \Phi_1}{\partial t} = -i(V + V_{sc} + 1) \Phi_1 -\dfrac{\partial \Phi_4}{\partial x} + i\dfrac{\partial \Phi_4}{\partial y} \\ \dfrac{\partial \Phi_4}{\partial t} = -i(V - V_{sc} - 1) \Phi_4 -\dfrac{\partial \Phi_1}{\partial x} - i\dfrac{\partial \Phi_1}{\partial y} \end{cases} }
Por fim, a equação em uma dimensão (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} ) é facilmente obtida: basta fazer Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{\partial \Phi_1}{\partial y} = \dfrac{\partial \Phi_4}{\partial y} = 0}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \dfrac{\partial \Phi_1}{\partial t} = -i(V + V_{sc} + 1) \Phi_1 -\dfrac{\partial \Phi_4}{\partial x} \\ \dfrac{\partial \Phi_4}{\partial t} = -i(V - V_{sc} - 1) \Phi_4 -\dfrac{\partial \Phi_1}{\partial x} \end{cases} }
Discretização
A equação de Dirac 1D pode ser escrita, na forma matricial, como
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \partial_t \mathbf{\Phi} = [-i\sigma_1\partial_x + \sigma_3] \mathbf{\Phi} + [V(t,x)I_2] \mathbf{\Phi} }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Phi} = (\phi_1, \phi_4)^T} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_2} é matriz identidade de dimensão 2. As matrizes de Pauli Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\sigma}} são escritas, aqui, como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_1 = \sigma_x} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_3 = \sigma_z} .
Para discretizar uma equação diferencial parcial como essa, é necessário discretizar o espaço e o tempo. Convenciona-se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta t} como um passo finito de tempo e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} como um passo finito no espaço, de tal forma que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_j = x_0 + jh, t_n = t_0 + n\Delta t} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j,n} são números inteiros. Define-se a notação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Phi}(t_n, x_j) = \mathbf{\Phi}_j ^n} e também Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(t_n,x_n) = V^n _j} . Discretiza-se as derivadas parciais explicitamente com uma expansão em série de taylor da própria função:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Phi^{n+1} _j} = \mathbf{\Phi^n _j} + \partial_t \mathbf{\Phi^n _j} \Delta t + \mathcal{O}(\Delta t ^2) }
Considerando uma derivada discretizada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_t \approx \partial_t} e truncando na primeira ordem:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_t\mathbf{\Phi^n _j} = \frac{\mathbf{\Phi^{n+1} _j} - \mathbf{\Phi^n _j}}{\Delta t} }
O processo é completamente análogo para a derivada espacial, porém para facilitar a aplicação do método mantém-se o espaço centrado em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_j} , em outras palavras faz-se uma expansão em torno de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{j-1}} , obtendo:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_x\mathbf{\Phi^n _j} = \frac{\mathbf{\Phi^n _{j+1}} - \mathbf{\Phi^n _{j-1}}}{2h} }
Com isso, obtém-se uma equação para um método explícito no tempo da equação de Dirac 1D.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \delta_t \mathbf{\Phi^n _j} = [-i\sigma_1\delta_x + \sigma_3] \mathbf{\Phi^n _j} + [V^n _jI_2] \mathbf{\Phi^n _j} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \frac{\mathbf{\Phi^{n+1} _j} - \mathbf{\Phi^n _j}}{\Delta t} = [-i\sigma_1\delta_x + \sigma_3] \mathbf{\Phi^n _j} + [V^n _jI_2] \mathbf{\Phi^n _j} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \mathbf{\Phi^{n+1} _j} = \mathbf{\Phi^n _j} + \Delta t[-i\sigma_1\delta_x + \sigma_3] \mathbf{\Phi^n _j} + \Delta t[V^n _jI_2] \mathbf{\Phi^n _j} }
Pode-se também desenvolver um método implícito no tempo fazendo a expansão de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Phi^{n-1} _j}} em torno de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_n} , obtendo:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_t\mathbf{\Phi^n _j} = \frac{\mathbf{\Phi^{n} _j} - \mathbf{\Phi^{n-1} _j}}{\Delta t} }
Ao aplicar esta aproximação na equação discretizada basta dar um passo a frente em todos os elementos, obtendo um método implícito no tempo, já que há dependência com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{n+1}} .
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \mathbf{\Phi^{n+1} _j} = \mathbf{\Phi^n _j} + \Delta t[-i\sigma_1\delta_x + \sigma_3] \mathbf{\Phi^{n+1} _j} + \Delta t[V^{n+1} _jI_2] \mathbf{\Phi^{n+1} _j} }
Método de Crank-Nicolson
O método de Crank-Nicolson (CN) consiste em uma média entre um método explícito e outro implícito no espaço. Utilizar-se-á a notação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Phi^{n+1/2} _j}} para representar justamente a média entre ambos os métodos, ou seja:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Phi^{n+1/2} _j} = \frac{\mathbf{\Phi^{n+1} _j} + \mathbf{\Phi^n _j}}{2} }
Define-se a notação:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V^{n+1/2} _j\mathbf{\Phi^{n+1/2} _j} = \frac{ V^{n+1} _j\mathbf{\Phi^{n+1} _j} + V^{n} _j\mathbf{\Phi^n _j}}{2} }
Dessa maneira, enuncia-se o método CN para a equação de Dirac 1D como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \delta_t \mathbf{\Phi^n _j} = [-i\sigma_1\delta_x + \sigma_3] \mathbf{\Phi^{n+1/2} _j} + [V^{n+1/2} _jI_2] \mathbf{\Phi^{n+1/2} _j} } ,
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_t, \delta_x } são as discretizações explícitas das derivadas.
Para que seja possível aplicar e estudar o método, é necessário passar da notação matricial para escalar:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \delta_t \mathbf{\Phi^n _j} = -i\sigma_1\delta_x\left(\frac{\mathbf{\Phi^{n+1} _j} + \mathbf{\Phi^n _j}}{2}\right) + \sigma_3\left(\frac{\mathbf{\Phi^{n+1} _j} + \mathbf{\Phi^n _j}}{2}\right) + I_2 \left(\frac{V^{n+1} _j \mathbf{\Phi^{n+1} _j} + V^n _j\mathbf{\Phi^n _j}}{2}\right) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \frac{\mathbf{\Phi^{n+1} _j} - \mathbf{\Phi^n _j}}{\Delta t} = -\frac{i}{2}\sigma_1\left[\frac{\mathbf{\Phi^{n+1} _{j+1}} - \mathbf{\Phi^{n+1} _{j-1}}}{2h} + \frac{\mathbf{\Phi^n _{j+1}} - \mathbf{\Phi^n _{j-1}}}{2h} \right] + \sigma_3\left(\frac{\mathbf{\Phi^{n+1} _j} + \mathbf{\Phi^n _j}}{2}\right) + I_2 \left(\frac{V^{n+1} _j \mathbf{\Phi^{n+1} _j} + V^n _j\mathbf{\Phi^n _j}}{2}\right) }
Isolando cada tempo em um lado da igualdade:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2\right]\mathbf{\Phi^{n+1} _j} + \frac{\Delta t}{4h}\sigma_1\left[\mathbf{\Phi^{n+1} _{j+1}} - \mathbf{\Phi^{n+1} _{j-1}}\right] = } Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[I_2 - \frac{i}{2}\Delta t\sigma_3 - \frac{i}{2}\Delta t V^{n} _j I_2\right]\mathbf{\Phi^{n} _j} - \frac{\Delta t}{4h}\sigma_1\left[\mathbf{\Phi^{n} _{j+1}} - \mathbf{\Phi^{n} _{j-1}}\right] }
Abrindo as matrizes Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_1, \sigma_3}
e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_2}
e operando-as sobre o vetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Phi}}
na equação, tem-se:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} +\frac{i\Delta t}{2} \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix} + \frac{i}{2}\Delta t V^{n+1} _j \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}\right) \begin{bmatrix} \psi^{n+1} _{1,j} \\ \psi^{n+1} _{4,j} \\ \end{bmatrix} +\frac{\Delta t}{4h} \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} \psi^{n+1} _{1,j+1} - \psi^{n+1} _{1,j-1} \\ \psi^{n+1} _{4,j+1} - \psi^{n+1} _{4,j-1} \\ \end{bmatrix} = \left(\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} -\frac{i\Delta t}{2} \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix} -\frac{i}{2}\Delta t V^{n} _j \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}\right) \begin{bmatrix} \psi^{n} _{1,j} \\ \psi^{n} _{4,j} \\ \end{bmatrix} -\frac{\Delta t}{4h} \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} \psi^{n} _{1,j+1} - \psi^{n} _{1,j-1} \\ \psi^{n} _{4,j+1} - \psi^{n} _{4,j-1} \\ \end{bmatrix} }
Pode-se realizar as operações matriciais e escrever duas equações escalares. Para facilitar a notação, utiliza-se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^n _j = \psi^n _{1,j}}
e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g^n _j = \psi^n _{4,j}}
:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \left[1 + \frac{i \Delta t}{2}(V^{n+1} _j + 1)\right]f^{n+1} _j + \frac{\Delta t}{4h}(g^{n+1}_{j+1} - g^{n+1}_{j-1}) = \left[1 - \frac{i \Delta t}{2}(V^{n} _j + 1)\right]f^{n} _j - \frac{\Delta t}{4h}(g^{n}_{j+1} - g^{n}_{j-1}) \\ \left[1 + \frac{i \Delta t}{2}(V^{n+1} _j - 1)\right]g^{n+1} _j + \frac{\Delta t}{4h}(f^{n+1}_{j+1} - f^{n+1}_{j-1} ) = \left[1 - \frac{i \Delta t}{2}(V^{n} _j - 1)\right]g^{n} _j - \frac{\Delta t}{4h}(f^{n}_{j+1} - f^{n}_{j-1}) \end{cases} }
Tem-se então um número Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}
de equações onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n}
é o número de elementos do espaço discretizado. Portanto o primeiro termo das duas equações gera uma matriz diagonal, pois multiplica os termos espaciais dependentes de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_j}
; já o segundo termo gera uma matriz tridiagonal com diagonal principal nula. Nota-se que os primeiros termos dos dois lados da igualdade são o conjugado um do outro: define-se, portanto, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha^n = 1 + \frac{i \Delta t}{2}(V^{n+1} _j + 1)}
e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = 1 + \frac{i \Delta t}{2}(V^{n+1} _j - 1)}
.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \alpha^{n+1}f^{n+1} _j + \dfrac{\Delta t}{4h}(g^{n+1}_{j+1} - g^{n+1}_{j-1}) = \alpha^{n^*}f^{n} _j - \dfrac{\Delta t}{4h}(g^{n}_{j+1} - g^{n}_{j-1} ) \\ \beta^{n+1}g^{n+1} _j + \dfrac{\Delta t}{4h}(f^{n+1}_{j+1} - f^{n+1}_{j-1} ) = \beta^{n^*}g^{n} _j - \dfrac{\Delta t}{4h}(f^{n}_{j+1} - f^{n}_{j-1}) \end{cases} }
Considerando que o potencial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V}
é só função da posição, escreve-se o método como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} Af^{n+1} + Bg^{n+1} = A^*f^n - Bg^n \\ Cg^{n+1} + Bf^{n+1} = C^*g^n - Bf^n \\ \end{cases} } ,
onde
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = \begin{bmatrix} \alpha & 0 & 0 & \cdots & 0\\ 0 & \alpha & 0 & \cdots & 0 \\ 0 & 0 & \alpha & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & \cdots & \cdots & \alpha \\ \end{bmatrix}; \quad B = \begin{bmatrix} 0 & \frac{\Delta t}{4h} & 0 & \cdots & 0\\ -\frac{\Delta t}{4h} & 0 & \frac{\Delta t}{4h} & \cdots & 0 \\ 0 & -\frac{\Delta t}{4h} & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 0 & \cdots & \cdots & -\frac{\Delta t}{4h} & 0 \\ \end{bmatrix}; \quad C = \begin{bmatrix} \beta & 0 & 0 & \cdots & 0\\ 0 & \beta & 0 & \cdots & 0 \\ 0 & 0 & \beta & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & \cdots & \cdots & \beta \\ \end{bmatrix} } .
Por fim, pode-se escrever o método resolvendo o sistema
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} f^{n+1} = F^{-1}D f^n -F^{-1}E g^n \\ g^{n+1} = J^{-1}G f^n - J^{-1}H g^n \\ \end{cases} } ,
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D = (B^{-1}A^* + C^{-1}B)} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E = (I + C^{-1}C^*)} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = (B^{-1}A - C^{-1}B)} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle G = (A^{-1}A^* + I)} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = (A^{-1}B + B^{-1}C^*)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J= (A^{-1}B - B^{-1}C)} .
Com isso, e com condições iniciais e de contorno bem estabelecidas, já é possível aplicar o método, dado que todas essas matrizes dependem somente dos parâmetros do sistema.
Estabilidade Crank-Nicolson
Utilizar-se-á o método de von Neumann para analisar a estabilidade do método de Crank-Nicolson para a equação de Dirac unidimensional. Para tanto, supõe-se que a função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Phi^{n} _j}} pode ser dada pela série de Fourier
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Phi^{n} _j} = \sum_{k=0}^{\inf} \mathbf{A}^{n}e^{ikqjh} }
Devido à independência linear de cada termo do somatório, ao substituir na equação do método haverá uma equação para cada ente do somatório. Se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\frac{\mathbf{A}^{n+1}}{\mathbf{A}^{n}}\right| \le 1} , então pode-se dizer que o método estável, já que dessa forma garante-se uma não divergência.
Aplica-se um termo geral da série de índice Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} no método CN para a equação de Dirac 1D:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2\right]\mathbf{A}^{n+1}e^{ikqjh} + \frac{\Delta t}{4h}\sigma_1\mathbf{A}^{n+1}\left[e^{ikq(j+1)h} - e^{ikq(j-1)h}\right] = \left[I_2 - \frac{i}{2}\Delta t\sigma_3 - \frac{i}{2}\Delta t V^{n} _jI_2\right]\mathbf{A}^{n}e^{ikqjh} - \frac{\Delta t}{4h}\sigma_1\mathbf{A}^{n}\left[e^{ikq(j+1)h} - e^{ikq(j-1)h}\right] }
Divide-se tudo por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ikqjh}} e isola-se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A}} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2 + \frac{\Delta t}{4h}\sigma_1\left(e^{ikqh} - e^{-ikqh}\right)\right]\mathbf{A}^{n+1}= \left[I_2 - \frac{i}{2}\Delta t\sigma_3 - \frac{i}{2}\Delta t V^{n} _jI_2 - \frac{\Delta t}{4h}\sigma_1\left(e^{ikqh} - e^{-ikqh}\right)\right]\mathbf{A}^{n} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2 + \frac{\Delta t}{4h}\sigma_1\left(\frac{\sin (kqh)}{2i}\right)\right]\mathbf{A}^{n+1}= \left[I_2 - \frac{i}{2}\Delta t\sigma_3 - \frac{i}{2}\Delta t V^{n} _jI_2 - \frac{\Delta t}{4h}\sigma_1\left(\frac{\sin (kqh)}{2i}\right)\right]\mathbf{A}^{n} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2 - \frac{i\Delta t}{4h}\sigma_1\left(\frac{\sin (kqh)}{2}\right)\right]\mathbf{A}^{n+1}= \left[I_2 - \frac{i}{2}\Delta t\sigma_3 - \frac{i}{2}\Delta t V^{n} _jI_2 + \frac{i\Delta t}{4h}\sigma_1\left(\frac{\sin (kqh)}{2}\right)\right]\mathbf{A}^{n} }
Nota-se que os termos que multiplicam o fator Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{A}} são o conjugado um do outro. Define-se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_l} como a componente l escalarda multiplicação da matriz Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_2 + \frac{i}{2}\Delta t\sigma_3 + \frac{i}{2}\Delta t V^{n+1} _j I_2 - \frac{i\Delta t}{4h}\sigma_1\left(\frac{\sin (kqh)}{2}\right)} pelo vetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} :
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{{A_l}^{n+1}}{{A_l}^{n}} = \frac{z^*}{z} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\frac{{A_l}^{n+1}}{{A_l}^{n}}\right| = \left|\frac{z^*}{z}\right| = \frac{|z^*|}{|z|} = 1 } ,
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} é sempre diferente de zero, visto que a parte real é dada por uma matriz identidade constante.
Mostra-se, portanto, que a razão entre os coeficientes da série de Fourier nunca diverge, ou seja, o método é incondicionalmente estável.
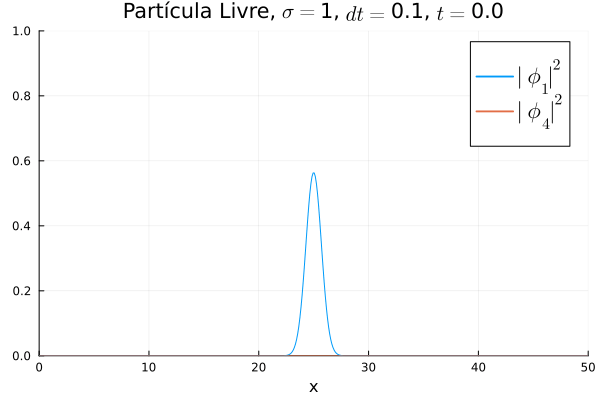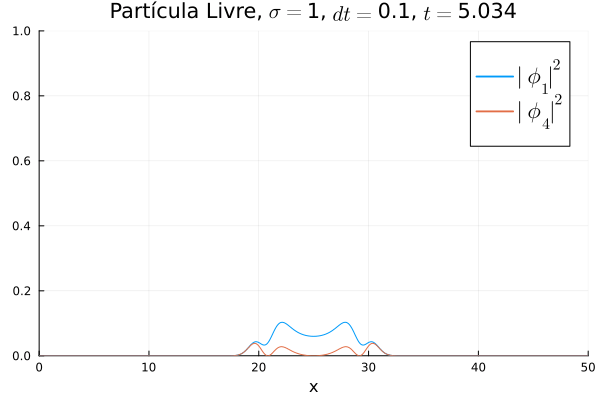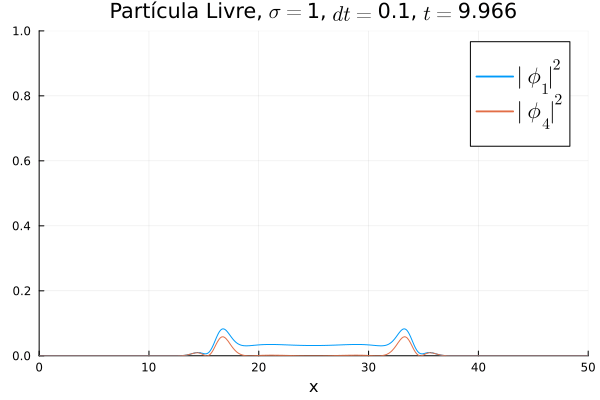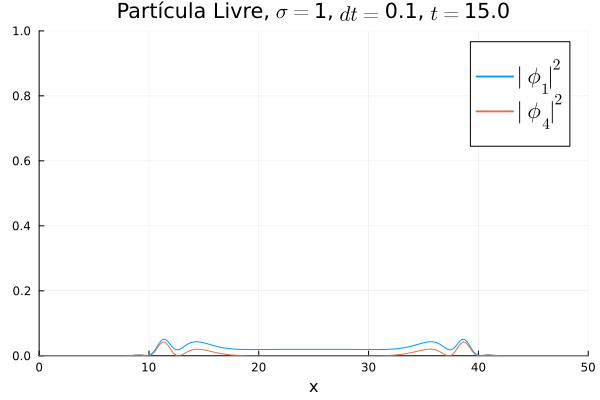
Simulações em Julia
Fez-se simulações do método de Crank-Nicholson para a equação de Dirac unidimensional em três configurações de potenciais diferentes: Nulo (Partícula Livre), Poço Infinito, Oscilador Harmônico Simples. Para todos os casos utilizou-se uma condição inicial de um pacote gaussiano de desvio padrão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} sob uma das componentes de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Phi}} e outra nula, o quadrado deste deve ter área unitária dentro da malha utilizada, por isso a constante de normalização deve ser Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\sqrt{\sigma\sqrt{\pi}}}} .
Segue trecho do código comum a todos as simulações realizadas:
Segue abaixo o código utilizado
Referências
- The quantum theory of the electron. Proceedings of the Royal Society of London A, v. 117, n. 778, p. 610–624, fev. 1928.
- SAKURAI, J. J. Mecânica quântica moderna. 2. ed. Porto Alegre: Bookman, 2012.
- BAO, W. et al. Numerical Methods and Comparison for the Dirac Equation in the Nonrelativistic Limit Regime. Journal of Scientific Computing, v. 71, n. 3, p. 1094–1134, jun. 2017.
- SOFF, G. et al. Solution of the Dirac Equation for Scalar Potentials and its Implications in Atomic Physics. Zeitschrift für Naturforschung A, v. 28, n. 9, p. 1389–1396, 1 set. 1973.
- THALLER, B. The Dirac equation. Berlin: Springer, 2010.