Nome: André Bracht Burmeister

Fluidos estão em todos os lugares e, portanto, estudá-los é muito importante. Como são objetos de estudo extremamente complicados, se fazem necessários modelos e simplificações. Uma simplificação muito usada é a análise do sistema em duas dimensões apenas, excluindo a terceira dimensão espacial.

O Modelo

Um fluido bidimensional pode ser modelado como $N$ partículas em um plano com densidade $\rho$ (partículas por $\sigma ^{2}$ ). O plano é um quadrado de lado $L={\sqrt {\frac {N}{\rho }}}$ . Para escolher a posição inicial de uma partícula, são escolhidas coordenadas $x$ e $y$ aleatórias entre $0$ e $L$ .

O Método de Monte Carlo

Para evoluir o sistema, usaremos caminhadas aletórias, escolhendo as partículas com o método de Monte Carlo[[1]]. O método de Monte Carlo consiste em escolher uma partícula aleatoriamente entre as $N$ . Então escolhemos aleatoriamente um deslocamento proposto para a partícula ${\vec {dL}}=d{\vec {x}}+d{\vec {y}}$ , onde $dx$ e $dy$ estão entre $0$ e $dL_{max}$ . A partícula só é realmente deslocada em ${\vec {dL}}$ de acordo com o Algoritmo de Metropolis-Hasting.

Algoritmo de Metropolis-Hasting

O Algoritmo de Metropolis-Hasting consiste em escolher se o movimento será ou não aceito usando a diferença de energia potencial entre o estado após o movimento e anterior ao movimento $dU=U(r_{2})-U(r_{1})$ . A probabilidade $P(dU)$ de aceitar o movimento é dada por:

 $P(dU)=min{(1,e^{-\beta dU})}$

Onde $\beta ={\frac {1}{T\cdot k_{B}}}$ , $T$ é a temperatura e $k_{B}$ é a constante de Boltzmann.

O Potencial de Lennard Jones

Para que o algoritmo funcione, precisamos então encontrar uma maneira de calcular a energia potencial de cada partícula. O potencial $U'$ que uma partícula causa na outra, pode ser aproximado a uma distribuição em termos da distância $r'$ entre elas:

 $U'(r')=4\epsilon \left[\left({\frac {\sigma }{r'}}\right)^{12}-\left({\frac {\sigma }{r'}}\right)^{6}\right]$

Esse potencial é conhecido como o potencial de Lennard-Jones, primeiro apresentado por ele em seu artigo ^[1].

Unidades Reduzidas

Como usar unidades do sistema internacional seria muito custoso computacionalmente, precisaremos usar unidades reduzidas em termos de $\epsilon$ , $\sigma$ e a constante de Boltzmann $k_{B}$ . As unidades utilizadas foram:

Grandeza	Comprimento	Temperatura	Energia	Densidade
Unidade	$\sigma$	$\epsilon /k_{B}$	$\epsilon$	$1/\sigma ^{3}$

Configuração de menor energia entre três partículas. Os círculos têm raio

2^{-5/6}\sigma

, metade da distância de menor potencial.

Usando as novas unidades o potencial de Lennard-Jones fica:

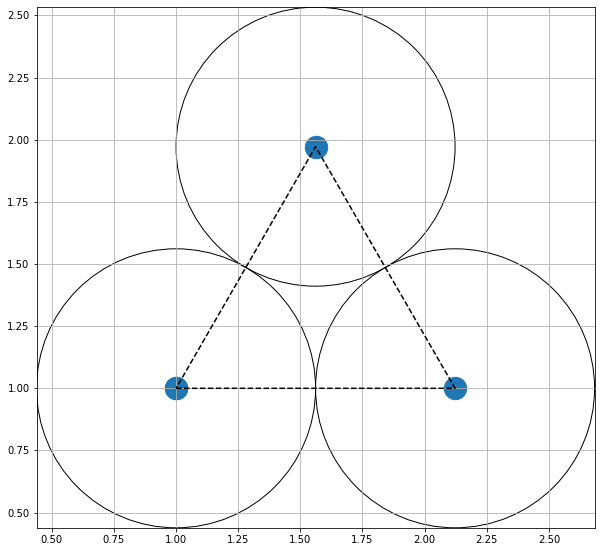
 $U(r)=4\left[\left({\frac {1}{r}}\right)^{12}-\left({\frac {1}{r}}\right)^{6}\right]$

O formato do potencial faz com que para raios grandes, a interação entre partículas seja muito pequena e, para raios muito pequenos, haja uma força de repulsão que tende ao infinito. Além disso, a região de potencial mínimo se encontra a $2^{1/6}\sigma \approx 1.12\sigma$ do centro da partícula. Ou seja, as partículas tendem a se organizar em uma configuração similar a da figura à direita, onde o raio dos círculos é ${\frac {2^{1/6}\sigma }{2}}=2^{-5/6}\sigma \approx 0.56$

Escolha de $dL_{max}$

Foi escolhido um deslocamento máximo $dL_{max}={\frac {2^{1/6}}{2}}=2^{-5/6}$ , pois isso faz com que o deslocamento não seja maior que metade da distância ao mínimo do potencial.

Resultados

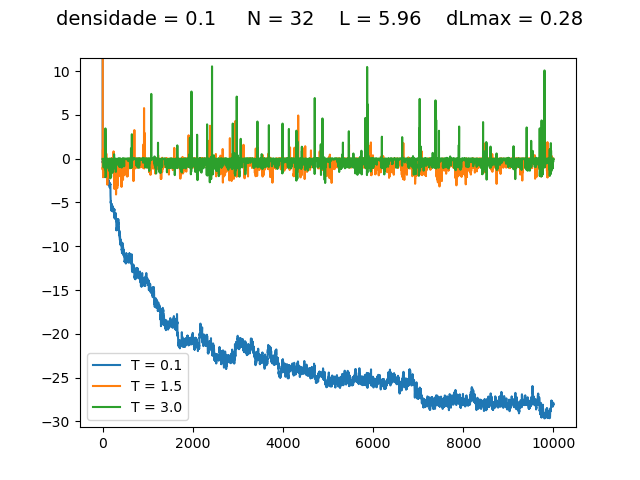
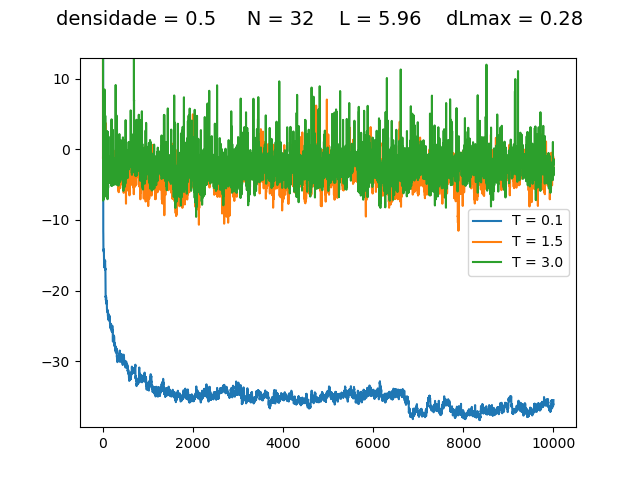
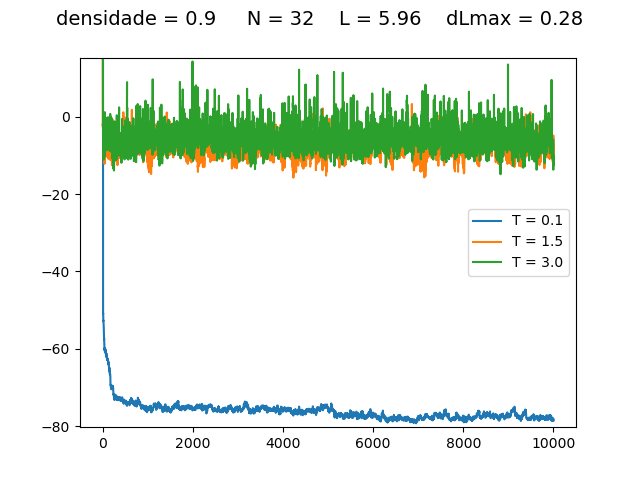
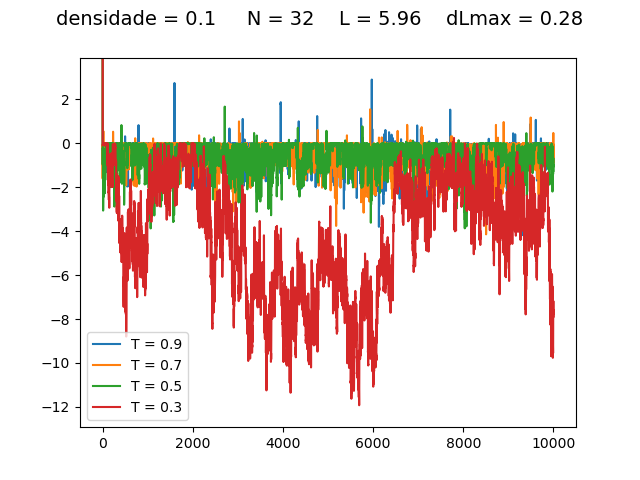
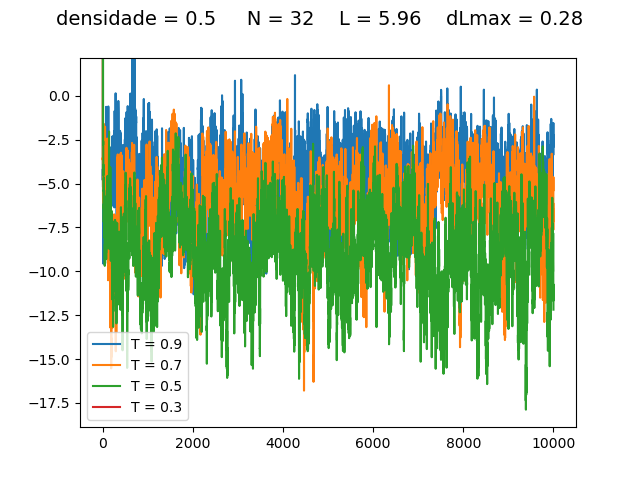
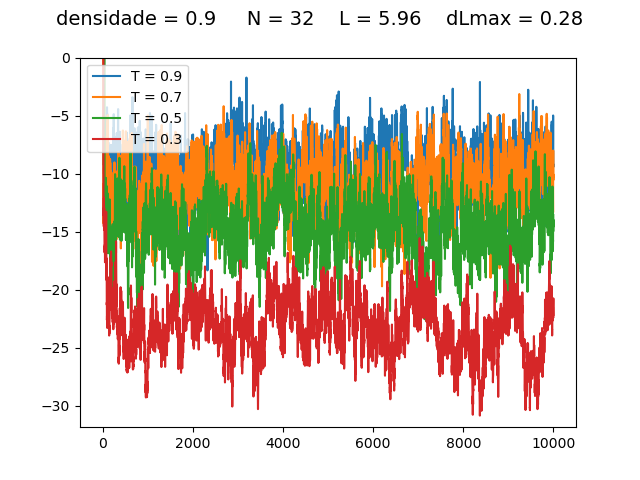
Energia

Medidas de energia $U$ a cada $MCS$ para diferentes densidades e temperaturas

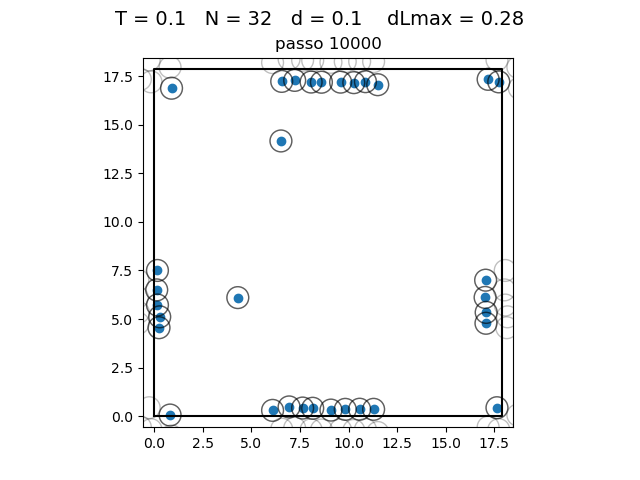
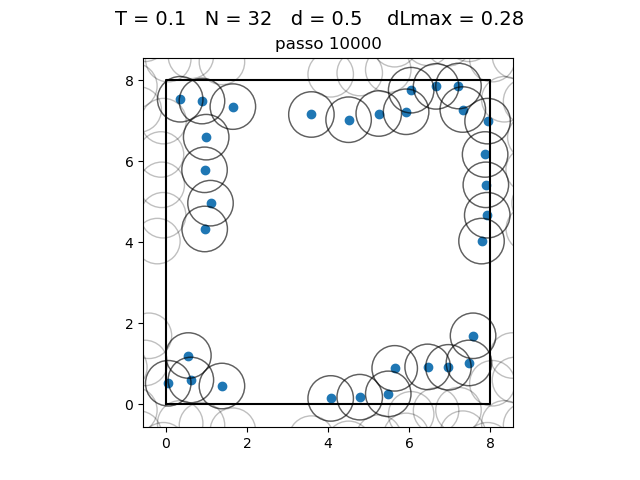
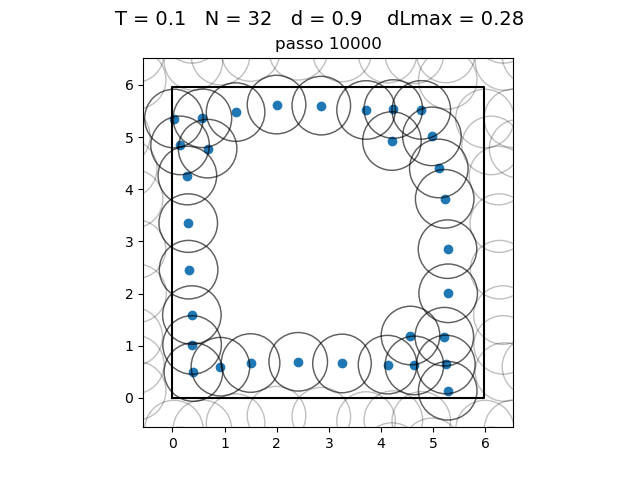
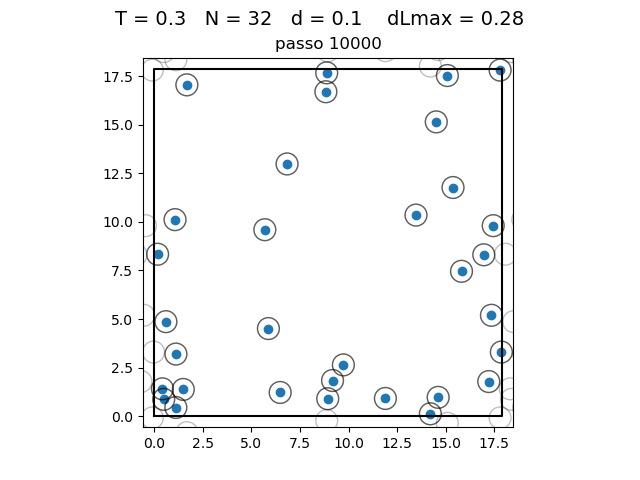
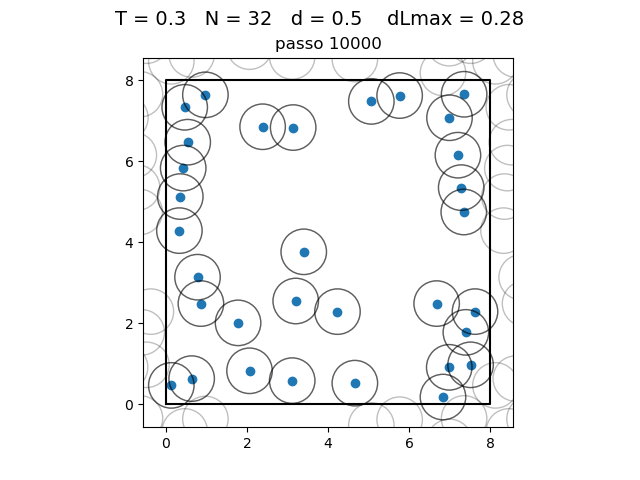
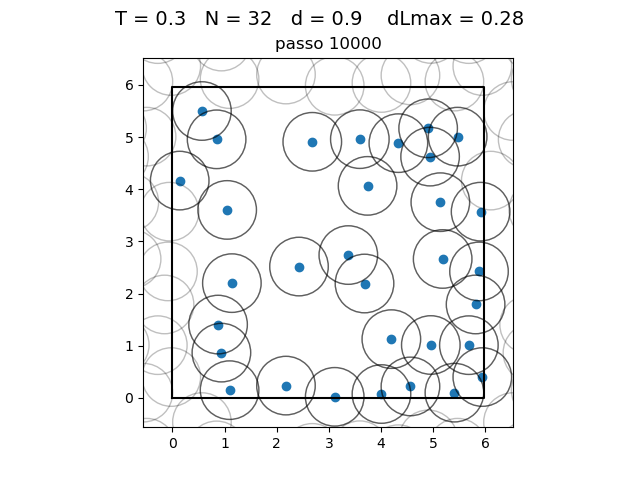
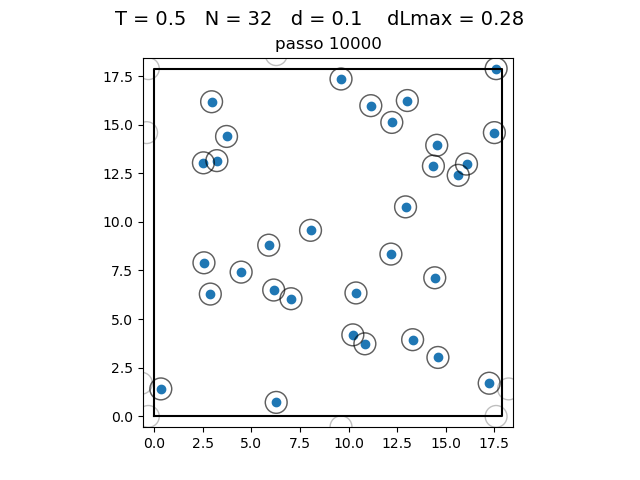
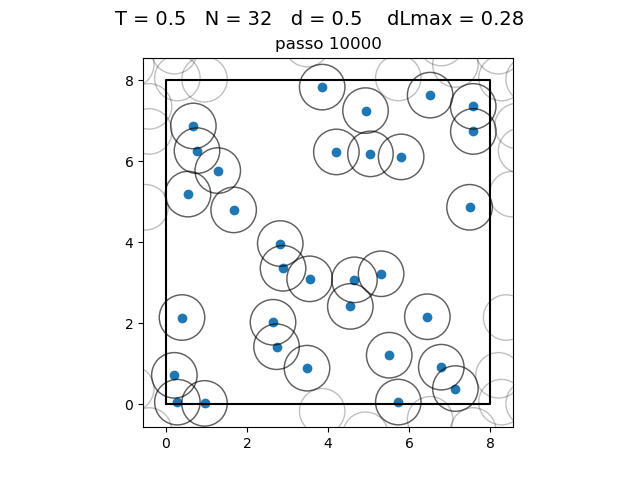
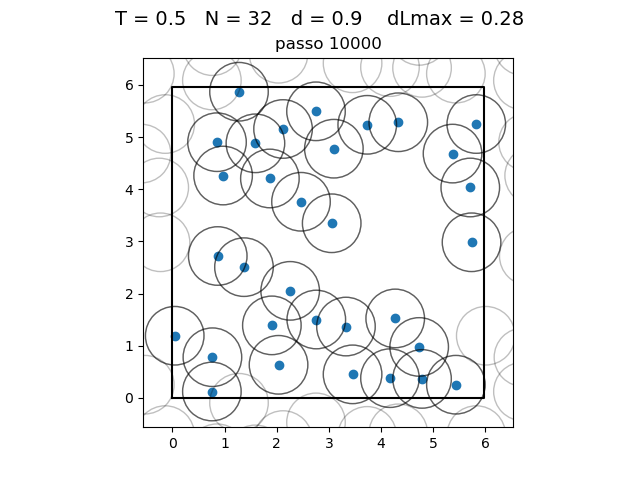
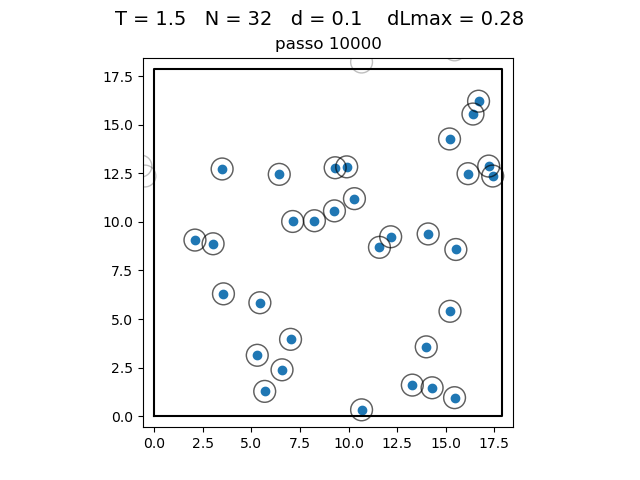
Transição de fase

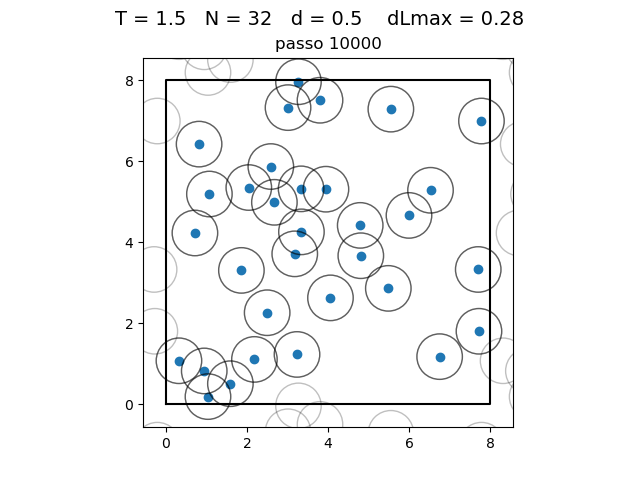
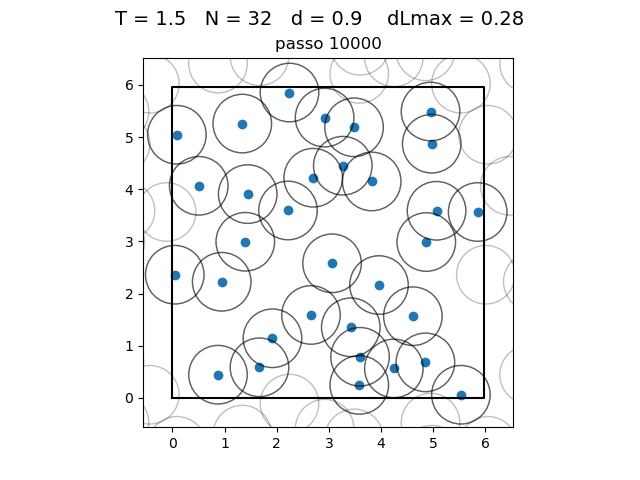
Posição das partículas ao fim da simulação com diferentes densidades e temperaturas

Código

"""lennard_jones.ipynb

Automatically generated by Colaboratory.

Original file is located at
    https://colab.research.google.com/drive/1jSPjBz0RXXWLEAzf3zcHgdlQpzjyO_ni

# Potencial de Lennard-Jones
# Monte Carlo no contínuo

#### Delete variables and import packages
"""

import numpy as np
from matplotlib import pyplot as plt
from matplotlib.animation import FuncAnimation 
import random
from scipy.optimize import bisect as find_root

"""## Simulação:

### Definições Numéricas:
"""

densidade = 0.1 #(2 ** (2/3)) * (3 ** (-1/2))  # partícula(s) por sigma^2 (partículas por área)
densidade_round = round(densidade, 2)
n_particles = 64
L = np.sqrt(n_particles / densidade)  # unidade de sigma
print(L)
dLmax = 0.1
MCS = 10000
eps = 1
T = .1
k = 1
beta = 1/(k*T)
raio = 2**(-5/6)

"""### Funcões:"""

def lennard_jones(r1, r2, L):  # r1 e r2 em unidades de sigma (na vdd seria r1/sig e r2/sig)
    dr = np.absolute(np.subtract(r2, r1))
    for i in np.arange(2):
        if dr[i] > 0.5:
            dr[i] = L - dr[i]

    r2 = (dr[0] ** 2) + (dr[1] ** 2)
    sr2 = 1/r2
    return 4 * (((sr2) ** 6) - ((sr2) ** 3))


def initial_energy(pos_particles, n_particles, L):
    U0 = 0
    for xxx in range(n_particles - 1):
        for yyy in range(xxx+1, n_particles):
            U0 += lennard_jones(pos_particles[:, xxx], pos_particles[:, yyy], L=L)
    return U0


def energy_var(p, pos_particles, n_particles, L, new_pos=np.zeros(2)):
    U1 = 0
    U2 = 0
    for i in range(n_particles - 1):
        j = (i + p + 1) % n_particles  # j vai ser todas as partículas 
        # exceto a partícula p (porque p interage com todas, menos com ela mesma)
        U1 += lennard_jones(pos_particles[:, j], pos_particles[:, p], L=L)
        U2 += lennard_jones(pos_particles[:, j], new_pos, L=L)
    return U2 - U1


def main_loop(dLmax, beta, n_particles, MCS, L, acceptance_array=False, 
              last_acceptance=False):
    
    pos_particles = L * np.random.random([2, n_particles])
    # Random positions:
    pos_MCS = np.zeros([MCS+1, 2, n_particles])
    pos_particles = pos_particles
    pos_MCS[0] = pos_particles

    # Energy:
    energy_arr = np.zeros(MCS+1)
    energy = initial_energy(pos_particles, n_particles, L=L)
    energy_arr[0] = energy

    # Acceptance:
    accepted = 0
    if acceptance_array:
        acceptance_arr = np.zeros(MCS)

    # Main Loop:
    for m in range(MCS):
        for _ in range(n_particles):
            p = random.randint(0, n_particles - 1)
            # change position:
            displacement = dLmax * ((2 * np.random.random([2])) - 1)
            new_pos = pos_particles[:, p] + displacement
            for i in range(2):
                if new_pos[i] < 0:
                    new_pos[i] += L
                elif new_pos[i] > L:
                    new_pos[i] -= L 
            dU = energy_var(p, pos_particles, n_particles, L, new_pos)
            if dU <= 0:
                pos_particles[0][p] = new_pos[0]
                pos_particles[1][p] = new_pos[1]
                energy += dU
                accepted += 1
            else:
                if random.random() < np.exp(-beta * dU):
                    pos_particles[0][p] = new_pos[0]
                    pos_particles[1][p] = new_pos[1]
                    energy += dU
                    accepted += 1
        if not (acceptance_array):
            pos_MCS[m+1] = pos_particles
            energy_arr[m+1] = energy

        if acceptance_array:
            acceptance_arr[m] = accepted / (n_particles*(m + 1))
    if acceptance_array:
        return acceptance_arr
    elif last_acceptance:
        return accepted / (n_particles*MCS)
    else:
        return pos_MCS, energy_arr, (accepted / (n_particles*(m + 1)))


def save_data(dLmax=dLmax, n_particles=n_particles, MCS=MCS, T=T, densidade=densidade):
    beta = 1 / (k*T)
    L = np.sqrt(n_particles / densidade)  # unidade de sigma
    print(L)
    pos, energy, acceptance = main_loop(dLmax=dLmax, beta=beta, n_particles=n_particles, 
                                        MCS=MCS, L=L)
    
    densidade_round = round(densidade, 3)
    # save positions:
    pos_reshaped = pos.reshape(pos.shape[0], -1)
    np.savetxt(f"positions_T{T}_N{n_particles}_d{densidade_round}_MCS{MCS}_dL_{dLmax}.txt", 
               pos_reshaped)

    # save energy:
    np.savetxt(f"energy_T{T}_N{n_particles}_d{densidade_round}_MCS{MCS}_dL_{dLmax}.txt", 
               energy)
    return pos, energy, acceptance


def open_pos(file, n_particles):
    loaded_pos = np.loadtxt(file)
    load_original_pos = loaded_pos.reshape(loaded_pos.shape[0], loaded_pos.shape[1] // n_particles, n_particles)
    return load_original_pos


"""### Rodar e salvar dados:

#### Rodar uma vez:
"""

dLmax = round(0.5*raio, 3)
pos, energy, acceptance = save_data(dLmax=dLmax)
print(f'dLmax={dLmax} \n beta={beta} \n n_particles={n_particles} \n MCS={MCS} \n\n pos[0]: \n {pos[0]}')
print(acceptance)

"""#### Rodar para vários T e rô:"""

dLmax = round(0.5*raio, 3)
n_particles = 32 
T_arr = np.array([0.1, 1.5, 3])
dens_arr = np.array([0.1, 0.5, 0.9])
for T in T_arr:
    print()
    print(f'T = {T}')
    for densidade in dens_arr:
        print(f'd = {densidade}')
        pos, energy, acceptance = save_data(dLmax=dLmax, n_particles=n_particles, MCS=MCS, T=T, densidade=densidade)
        #print(f'dLmax={dLmax} \n beta={beta} \n n_particles={n_particles} \n MCS={MCS} \n\n pos[0]: \n {pos[0]}')
        print(f'acceptance = {acceptance}')


"""
## Testes:

### Encontrar deslocamento máximo:
Testando valores:
"""

def testing_dL(possible_dL, times):
    for l in possible_dL:
        accept = np.zeros(times)
        for d in range(times):
            accept[d] = main_loop(dLmax=l*L, last_acceptance=True, acceptance_array=False)
        print(f'dLmax = {l}*L, acceptance = {np.mean(accept)}')

# Roda mais geral:
possible_dL = np.round(0.1*np.arange(1, 10), 1)
testing_dL(possible_dL, 5)

# Ajuste fino:
possible_dL = np.round(0.01*np.arange(10, 14), 3)
testing_dL(possible_dL, 50)

# Novo dLmax:
dLmax = 0.12*L
print(dLmax)

"""### Comportamento da acceptance:"""

def acceptance_behaviour(possible_dL, times):
    for d in range(times):
        fig, axes = plt.subplots(1, len(possible_dL), figsize=(20, 5))
        fig.suptitle(f'T = {T}   N = {n_particles}   d = {densidade_round}    dLmax = {round(dLmax, 2)}', fontsize=14)
        for l in range(len(possible_dL)):
            print(f'{l+1}/{len(possible_dL)}, {d+1}/{times}')
            acceptance = main_loop(dLmax=possible_dL[l]*raio, acceptance_array=True)
            axes[l].plot(np.arange(len(acceptance)), acceptance)
            axes[l].set_ylim([0, 1])
            axes[l].set_title(f'dLmax = {possible_dL[l]}*2^(-5/6)')
        plt.show()
        plt.close()

# Plotando acceptance
possible_dL = np.round(0.2*np.arange(1, 5), 1)
acceptance_behaviour(possible_dL, 1)

# Mais fino:
possible_dL = np.round(np.concatenate([0.0001*np.arange(1, 6)]), 4)
acceptance_behaviour(possible_dL, 1)


"""
## Figuras

### Intial and final positions:
"""

def scatter_pos(pos, indices, T, L, circles=True):
    graphs = len(indices)
    fig, axes = plt.subplots(1,graphs)
    fig.suptitle(f'T = {T}   N = {n_particles}   d = {densidade_round}    dLmax = {round(dLmax, 2)}', fontsize=14)

    for j in range(graphs):
        k = indices[j]
        if circles:
            # draw the circles where they are
            for i in range(n_particles):
                c = plt.Circle([pos[k][0][i], pos[k][1][i]], raio, fill=False, edgecolor='black', alpha = 0.5)
                axes[j].add_patch(c)
            # draw the circle's projections:
            for a in range(-1, 2):
                for b in range(-1, 2):
                    for i in range(n_particles):
                        c = plt.Circle([pos[k][0][i] + a*L, pos[k][1][i] + b*L], raio, fill=False, edgecolor='black', alpha=0.25)
                        axes[j].add_patch(c)
        
        points = axes[j].scatter(pos[k][0], pos[k][1])
        margem = raio
        axes[j].plot([0, L, L, 0, 0], [0, 0, L, L, 0], color='black')
        axes[j].axis([-margem, L + margem, -margem, L + margem], 'equal')
        axes[j].grid(visible=False)
        axes[j].set_aspect("equal")
        axes[j].set_title(f'passo {k}')
    return fig, axes, points


for T in T_arr:
    print()
    print(f'T = {T}')
    for densidade in dens_arr:
        print(f'd = {densidade}')
        densidade_round = round(densidade, 3)
        file_end = f"_T{T}_N{n_particles}_d{densidade_round}_MCS{MCS}_dL_{dLmax}"
        file_name = f"positions{file_end}.txt"
        pos = open_pos(file_name, n_particles=32)

        L = np.sqrt(n_particles / densidade)  # unidade de sigma
        plot = scatter_pos(pos=pos, indices=[0, pos.shape[0] - 1], T=T, L=L, circles=True)
        plt.show()
        plt.savefig(f"first_last_positions{file_end}.png")
        plt.close()

"""### Energy:"""

def y_limits(energy):
    energy_hist_range = energy[int(round(0.1*len(energy), 0)):]
    return [min(energy_hist_range)-1 , max([0, max(energy_hist_range) + 1])]

"""#### Energy graph:"""

for T in T_arr:
    print()
    print(f'T = {T}')
    for densidade in dens_arr:
        print(f'd = {densidade}')
        file_end = f"_T{T}_N{n_particles}_d{densidade_round}_MCS{MCS}_dL_{dLmax}"
        energy = np.loadtxt(f"energy{file_end}.txt")

        # Plot:
        fig, ax = plt.subplots(1, 1)
        titulo = f'T = {T}   N = {n_particles}   d = {densidade_round}    L = {round(L, 2)} \n dLmax = {round(dLmax, 2)}    acceptance = {round(acceptance, 2)}'
        fig.suptitle(titulo,
                    fontsize=14)
        energy_range = energy
        ax.plot(np.arange(len(energy_range)), energy_range)
        limites = y_limits(energy)
        print(limites)
        ax.set_ylim(limites)
        plt.show()
        plt.savefig(f"energy_graph{file_end}.png")
        plt.close()


        # Histogram:
        fig, ax = plt.subplots(1, 1)
        fig.suptitle(titulo,
                    fontsize=14)
        ax.hist(energy[100: ], density=True)
        ax.set_xlabel('energy')
        plt.show()
        plt.savefig(f"energy_histogram{file_end}.png")
        plt.close()

"""#### Energy histogram:"""



"""## Animação"""

file_name = f"positions_T{T}_N{n_particles}_d{densidade_round}_MCS{MCS}_dL_{dLmax}.txt"
print(file_name)

start = 0
end = len(pos)
pos = open_pos(file_name)[start:end]
fig, ax = plt.subplots(1,1, figsize=(5, 6))
fig.suptitle(f'T = {T}   N = {n_particles}   d = {densidade_round}    L = {round(L, 2)} \n dLmax = {round(dLmax, 2)}    acceptance = {acceptance}',
             fontsize=14)
margem = raio
ax.axis([-margem, L + margem, -margem, L + margem], 'equal')
ax.grid()
ax.set_aspect("equal")
ax.set_title(f'passo {k}')

c = []
for i in range(n_particles):
    c.append(plt.Circle([pos[0][0][i], pos[0][1][i]], raio, fill=False, color='lightgrey'))
    ax.add_patch(c[i])
scatter_points = ax.scatter(pos[0][0], pos[0][1], s=1000)


def animate(i):
    for k in range(n_particles):
        c[k].center = (pos[i][0][k], pos[i][1][k])
    scatter_points.set_offsets(pos[i].T)
    return scatter_points


anim = FuncAnimation(fig, animate, interval = 10, frames = end-start-1)

anim_file = f'animacao_T{T}_N{n_particles}_d{densidade_round}_MCS{MCS}_dL_{dLmax}.mp4'
print(anim_file)
anim.save(anim_file, writer = 'ffmpeg', fps = 20)

"""## Imagens:

### Raio:
"""

x0 = 1
y0 = 1
l = 2 * (2 ** 1/6)
triX = [x0, x0+l, x0+(l/2)]
h = np.sqrt(3)*l/2
triY = [y0, y0, y0 + h]

triX.append(triX[0])
triY.append(triY[0])

fig, ax = plt.subplots()

for i in range(3):
    c = plt.Circle([triX[i], triY[i]], l, alpha=0.5)
    c = plt.Circle([triX[i], triY[i]], l, alpha=0.5)
    c = plt.Circle([triX[i], triY[i]], l, alpha=0.5)
    ax.add_patch(c)

ax.plot(triX, triY, color = 'b')
ax.axis([x0-(l/2), x0 + (3*l/2), y0 - (l/2), y0 + h + l/2], 'equal')
ax.grid()
ax.set_aspect("equal")
plt.show()
plt.close()

"""### Potencial Lennard Jones:"""

def lennard_jones1d(r):
    sr6 = 1/(r ** 6)
    return 4 * (((sr6) ** 2) - (sr6))


xx = np.linspace(0, 4, 100)
yy = lennard_jones1d(xx)
fig, ax = plt.subplots(1, 1, figsize=(10, 4))
ax.plot([-10, 10], [0, 0], color='black')
ax.plot(xx, yy)
ax.set_ylabel('U(r)')
ax.set_xlabel('r')
ax.set_ylim([-1.5, 5])
ax.set_xlim([0, 3])
plt.show()
fig.savefig('lennard_jones_potential.png')
plt.close()

↑ J E Lennard-Jones 1931 Proc. Phys. Soc. 43 461

[1] J E Lennard-Jones 1931 Proc. Phys. Soc. 43 461

[1]

Potencial de Lennard-Jones

Índice

O Modelo

O Método de Monte Carlo

Algoritmo de Metropolis-Hasting

O Potencial de Lennard Jones

Unidades Reduzidas

Escolha de $dL_{max}$

Resultados

Energia

Transição de fase

Código

Menu de navegação

Potencial de Lennard-Jones

O Modelo

O Método de Monte Carlo

Algoritmo de Metropolis-Hasting

O Potencial de Lennard Jones

Unidades Reduzidas

Escolha de d L m a x {\displaystyle dL_{max}}

Resultados

Energia

Transição de fase

Código

Menu de navegação

Pesquisa

Escolha de $dL_{max}$