Equações de Laplace e Poisson
Grupo: Augusto M Giani e Henrique
O objetivo deste trabalho é implementar os métodos de Relaxação, Gauss-Seidel e SOR (Simultaneous OverRelaxation) em problemas de eletroestática, resolvidos pelas equações de Laplace e Poisson. Também temos como objetivo comparar seus resultados: erro entre os métodos e a solução analítica, tempo para estabilização das soluções.
Eletroestática
A Equação de Laplace descreve o Potencial Elétrico (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi} ) de uma determinada região num espaço que não possui nenhuma densidade de carga elétrica (corpo carregado):
ou na sua versão em 2 dimensões[1]: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^{2}\Phi}{\partial x^2} + \frac{\partial^{2}\Phi}{\partial y^2} = 0}
Quando neste determinado espaço, delimitado pelas condições de contorno, existe uma densidade de carga, o campo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi} já não se iguala mais à zero, mas sim à densidade de cargas dentro daquela região, sendo descrito agora pela Equação de Poisson:
ou na sua versão em 2 dimensões[1]: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial ^2\Phi}{\partial x^2} + \frac{\partial^{2}\Phi}{\partial y^2} = \frac{-\rho(x,y)}{\epsilon_0}}
Método de Relaxação
Como podemos ver ambas as equações não dependem do tempo, porém podemos usar um truque para resolver estas equações aplicando o método FTCS (Forward Time Central Space) em uma equação parecida, e fazer a evoluçao temporal durar tempo sufiente para a solução convergir (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t \rightarrow \infty} ). Esta operação é chamada de Método de Relaxação.
O que usamos para convergir à solução da Equação de Laplace foi uma equação de difusão genérica:
Fazendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t \rightarrow \infty} , para a equação de difusão temos a intuição que dada condição inicial estacionária, a solução não diverge e "relaxa" para uma função que não depende mais do tempo:
Com isso: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial f}{\partial t} = 0} , e chegando assim à Equação de Laplace e possibilitando chegar na discretização da Equação de Poisson. Então basicamente utiliza-se da mesma discretização de uma equação de difusão, porém a evolução temporal só serve para convergirmos à solução da Equação de Laplace com as condições iniciais que propomos. Os métodos de Jacobi, Gauss-Seidel e SOR são considerados Métodos de Relaxação[2].
Métodos Numéricos
Foram implementadas as seguintes discretizações para os problemas de eletroestática.
Método de Jacobi
Equação de Laplace
Para equação de Laplace partimos de:
Discretizando, primeiro chegamos que:
Seguindo mesmo procedimento do método de FTCS, temos a mesma condição de estabilidade:
No nosso algoritmo ultizamos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x = \Delta y} então obtivemos a condição de estabilidade:
Para o algoritmo de Jacobi (Relaxação) escolhemos o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{4}} e com isso resulta na equação final:
onde n representa o passo no tempo, i representa o passo em X e j representa o passo em Y. A constante Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} somente representava uma similaridade com a equação de difusão para demonstrar que este valor não interfere na equação final, ele sequer aparece (portanto podemos desconsiderá-lo, como faremos na equação de Poisson).
Equação de Poisson
Partindo de:
chegamos em:
Para nosso problema Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x = \Delta y} , então multiplicando os dois lados por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\Delta x^2}{\Delta t}} , chegamos em:
E finalmente, aplicando a condição de estabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\Delta t} {\Delta x^2} = \frac{1}{4}} e cancelando os termos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi^{n}_{i,j}} :
Método de Gauss-Seidel
O Método de Gauss-Seidel adianta (no tempo) a chegada da solução estacionária, utilizando termos que já foram calculados num passo anterior de tempo para calcular o ponto atual. Isto é, ao fazer a iteração, para calcular o valor de algum ponto são utilizados dois valores que já foram atualizados na mesma iteração e dois que foram calculados na iteração passada. Com isso é de se esperar que há uma variação mais rápida dos valroes do plano, quando comparado com o método anterior.
Equação de Laplace
Para equação de Laplace, obetemos a seguinte equação de iteração:
Equação de Poisson
Como pode-se notar, o termo que distingue a Equação de Laplace para a Equação de Poisson é apenas o termo que soma Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{1}{4}\frac{\Delta x^2 \rho_{i,j}}{\epsilon_0} \right)} ao lado direito da equação. Assim temos a seguinte equação de iteração:
Método SOR (Simultaneous Overrelaxation)
Como pode-se notar nas equações (é mais intuitivo na forma discretizada da Equação de Laplace), a atualização de um ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi^{n+1}_{i,j}} é feita através de uma espécie de "média" dos pontos, no tempo anterior, ao seu arredor (o ponto acima, à direita, à esquerda e abaixo na matriz dos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi_{i,j}} ). O método introduz nesse cálculo de "média" (ainda no método de Gauss-Seidel), pesos para a contribuição dos pontos da vizinhança e também um peso para o próprio ponto no tempo anterior.
Equação de Laplace
Aplicando os pesos na forma discretizada da equação de Laplace pelo método de Gauss-Seidel:
Equação de Poisson
Da mesma forma aplicamos os pesos na forma discretizada da equação de Poisson pelo método de Gauss-Seidel:
Onde:
E Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} é dado por:
r = Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} cos( \frac{\pi}{L_x} ) + \frac{1}{2} cos( \frac{\pi}{L_y} )}
No nosso caso, temos que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_x=L_y=L} , portanto o Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_{opt}} é:
Todas as equações em Azul descritas acima foram implementadas em nossos códigos.
Problemas propostos
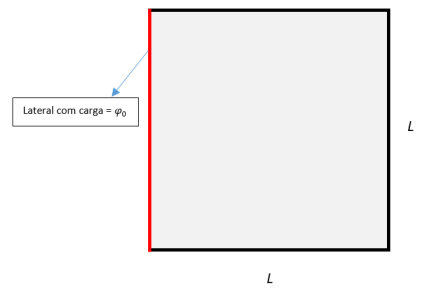
Problema da borda carregada
Equação de Laplace aplicada a um plano Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L\times L} com uma das quatro "bordas" carregada. Consideramos as dimensões de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_x} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_y} como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} (um plano quadrado) para facilitar os cálculos.
Condições iniciais e de contorno:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \Phi(x = 0,y) = \Phi_{0} = 1 \\ \Phi(x = L,y) = \Phi(x,y = 0) = \Phi(x,y = L) = 0\\ \end{cases} }
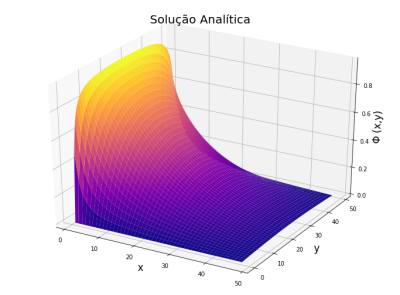
Para a solução analítica do problema temos que:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(x,y) = \Phi_{0} \sum^{\infty}_{i=1,2,3,...}\frac{4}{\pi n} \left( \frac{n\pi x}{L} \right) \frac{\sinh(n\pi y/L)}{\sinh(n\pi)} }
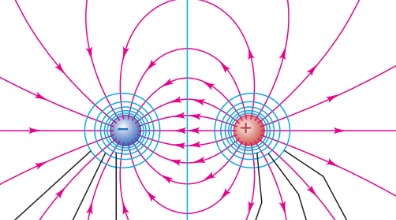
Problema do Dipolo Elétrico
Equação de Poisson considerando uma dipolo elétrico como densidade de carga Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho(x,y)} :
Utilizamos como condições iniciais e de contorno do problema:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} \rho(x = L/2,y = L/4) = 1 \\ \rho(x = L/2,y = 3L/4) = -1\\ \Phi(x = 0,y) = \Phi(x = L,y) = \Phi(x,y = 0) \Phi(x,y = L) = 0\\ \end{cases} }
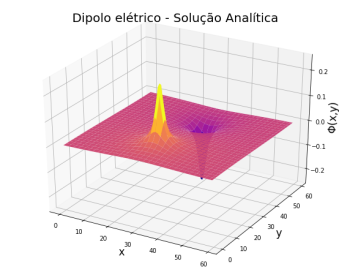
Temos a solução do potencial eletroestático de cada partícula no plano dada por:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(x,y)=\frac{1}{4\pi\epsilon_{0}}\frac{q}{\sqrt{x^2+y^2}}}
Onde consideramos as constantes com sendo = 1 para facilitar a modelagem do problema.
Implementação
Implementamos as simulações em Python3, no ambiente Colab da Google. Junto com as soluções numéricas também implementamos a solução analítica de um problema para compararmos com a solução numérica
Os códigos se encontram no final desta Wiki, mas uma observação geral é que além de utilizarmos as equações destacadas em Azul para implementar as soluções, é importante lembrar que o resultado final só é atingido quando iteramos as soluções no "tempo", então é preciso iterar os elementos da matriz no espaço, mas também fazer ela evoluir com o tempo, exemplo para o algoritmo de Jacobi, Equação de Laplace:
### Exemplo da evolução temporal no método de relaxação ###
# P é a matriz do potencial no tempo n
# Q é a matriz do potencial no tempo n+1
while t < tmax: # Loop temporal
for i in range(1,L+1): # Loop em x
for j in range(1,L+1): # Loop em y
Q[i][j] = (P[i+1][j] + P[i-1][j] + P[i][j+1] + P[i][j-1])/4
P = Q.copy()
t = t + td
plt.plot(x,y,P)
Lembrando que estamos resolvendo o problema em 2D, por isso P e Q são matrizes, onde cada elemento representa um ponto no plano. Como pode-se ver, somente é plotado um gráfico, ou somente se é considerado como resultado final o estado final do vetor P, depois que ele sai do loop while. Esta lógica foi usada para todos os métodos que aplicamos[3] [4].
Resultados do problema da Borda Carregada
Apresentamos as seguintes soluções do problema com a Equação de Laplace pois já é um problema bem documentado com resultados mais palpáveis para compararmos e analisarmos a implementação dos métodos.
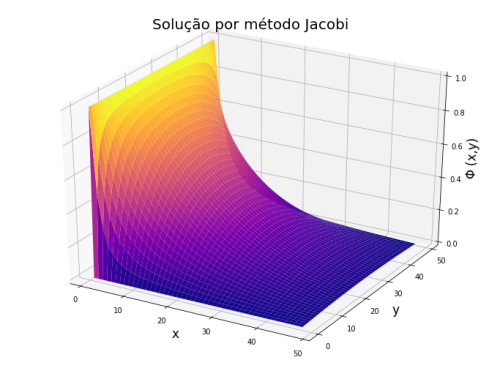
Método de Jacobi
Obtivemos a seguinte solução pelo método explícito:
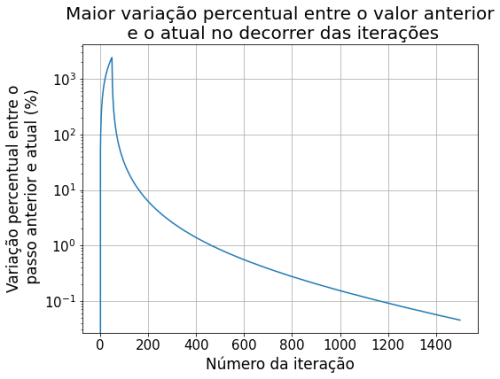
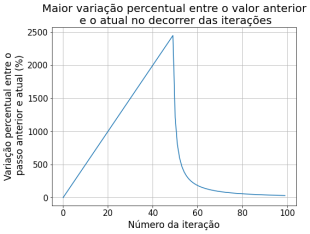
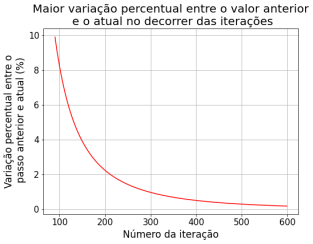
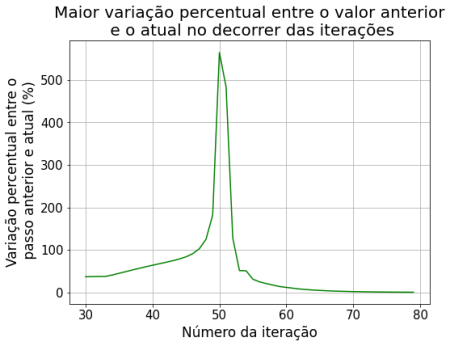
Comparando com a iteração no passo de tempo anterior, obtivemos as seguintes diferenças entre o passo n+1 e o passo n:
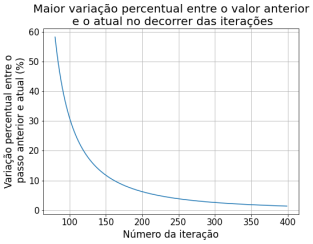
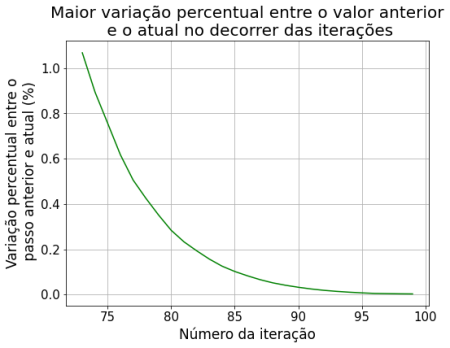
Dando mais zoom nas iterações futuras podemos ver que as variações (%) se tornam menores, indicando que o método converge para a solução estacionária.
O maior erro aqui considerado no gráfico é do ponto do plano de 50x50 do nosso problema que apresentou maior diferença de valor em relação à iteração temporal anterior. Utilizamos o mesmo padrão de resultado de erro nos outros métodos.
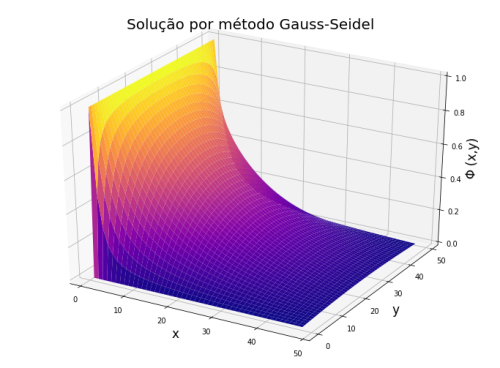
Método de Gauss-Seidel
Obtivemos a seguinte solução pelo método de Gauss-Seidel:
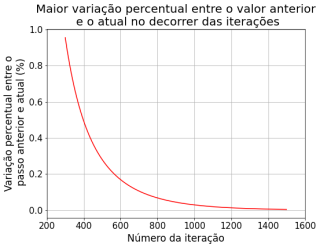
Comparando com a iteração no passo de tempo anterior, obtivemos as seguintes diferenças entre o passo n+1 e o passo n:
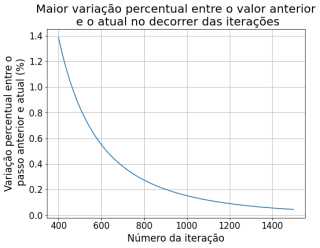
Aplicamos zoom nas iterações futuras, onde podemos ver que as variações (%) se tornam tão pequenas que praticamente o método converge para a solução estacionária. Iremos discutir posteriormente que esta solução converge, com erro bem menor, antes do que o método de Jacobi
Método SOR (Simultaneous Overrelaxation)
Obtivemos a seguinte solução aprimorando o método de Gauss-Seidel para Simultaneous OverRelaxation:
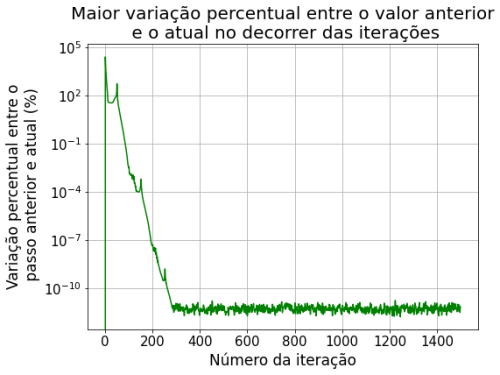
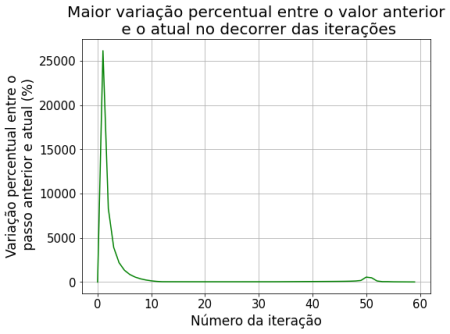
Comparando com a iteração no passo anterior, podemos fazer a seguinte análise:
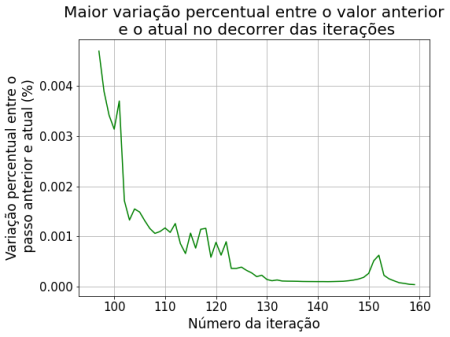
Aplicando zoom nas iterações futuras, onde podemos notar um comportamento anômalo no "erro" em iterações múltiplas de 50 (tamanho da grade).
Resultados do problema do Dipolo Elétrico
Para o Problema do Dipolo Elétrico (através da Equação de Poisson) compararmos e analisarmos a implementação dos métodos focando no erro proporcionado pelos métodos numéricos.
Método de Gauss-Seidel
A implementação foi realizada conforme descrito na seção de Métodos Numéricos.
Método de SOR
Assim como a implementação do método de Gauss-Seidel, obtivemos os seguintes resultados com o método de SOR.
Discussão
Problema da Borda Carregada
Resultados do Método de Jacobi
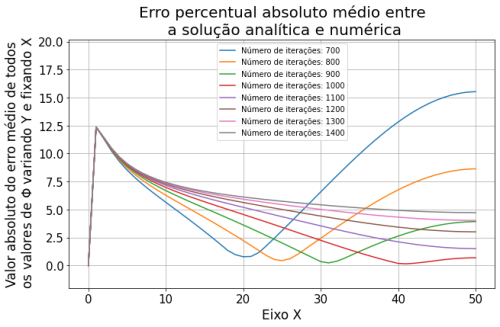
Primeiro começamos pelo Método de Jacobi, também conhecido por FTCS, modelando um problema conhecido para compararmos a precisão de nossos algoritmos com a solução analítica. Ao resolver o potencial elétrico nas condições do problema da borda carregada obtivemos o comportamento da curva igual ao esperado analiticamente.
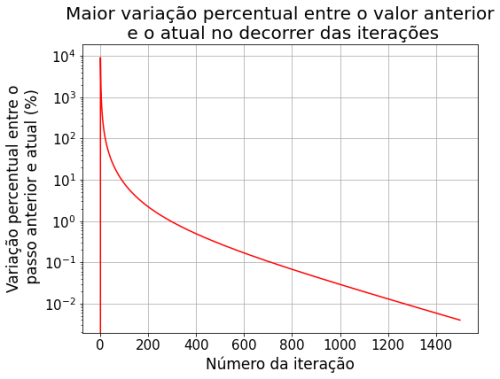
Sobre o método de relaxação observa-se que nas primeiras iterações há uma variação muito grande dos valores da solução. Nas primeiras 60 iterações, os valores do potencial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi} variaram em até 2500% em relação ao passo anterior. Percebe-se que a partir de 160 iterações começa a ter uma variação menor que 10%, e a partir de 1200 passos já atingimos uma variação menor que 0.1%. Por esse método convergir mais devagar, assumimos os 1500 passos pois sabíamos que os outros métodos iriam convergir com menos iterações. Decidimos comparar os métodos com 1500 passos, a partir disso já não notamos mais variação significativa.
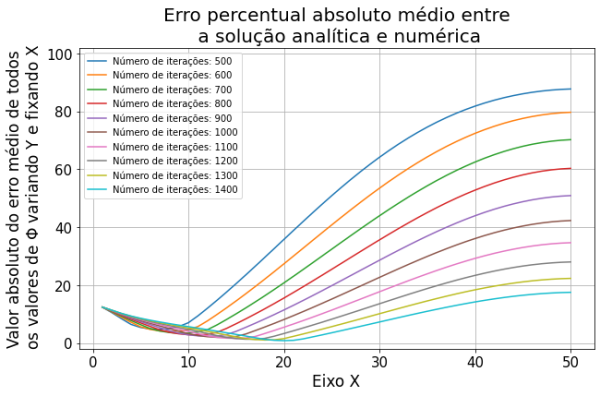
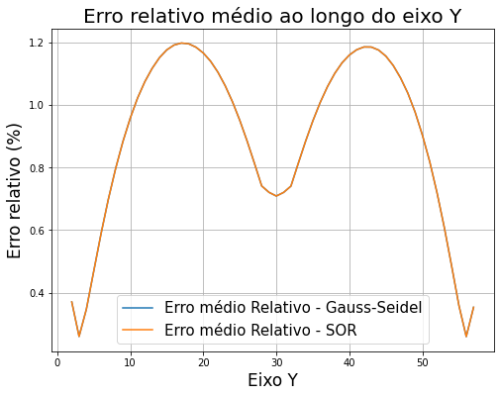
O gráfico acima representa a comparação entre o método numérico e a solução analítica do problema. A maneira que escolhemos para verificar a acurácia do método foi a seguinte: fixamos o valor de x e comparamos todos os valores da solução numérica e analítica percorrendo em y. Nessa comparação fizemos a média dos valores absolutos percentuais do erro entre as soluções, com isso temos a média do erro ao longo do eixo X, para diferentes iterações. Esta análise foi repetida para todas as implementações seguintes.
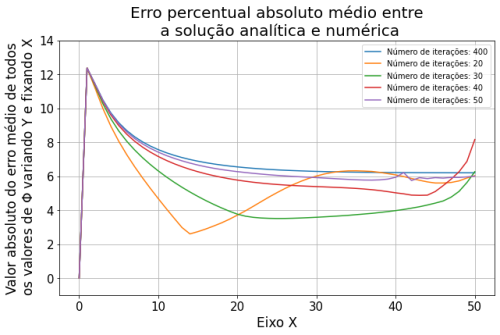
Resultados do Método de Gauss-Seidel
A implementação numérica do Método de Gauss-Seidel atingiu o mesmo comportamento que a solução analítica, assim como método FTCS. Observando os gráficos da diferença dos valores de por iteração (mostrados na seção de Resultados'), pode-se notar que a variação menor que 10% encontra-se a partir da 90ª iteração (já no método de Jacobi observou-se esta variação somente pelo 160º passo). Já esperávamos que o método de Gauss-Seidel convergisse mais rápido, pelo fato da equação de iteração utilizar dois termos calculados no passo n e dois termos do passo n-1, enquanto o método de jacobi considera os quatro termos do passo n-1.
Os gráficos acima representam o mesmo erro médio percentual absoluto utilizado para comparar o Método de Jacobi. Porém para este método ressaltamos o resultado das soluções acima de 1000 passos (gráfico da direita). Verificamos que para o número de iterações menores o erro foi ligeiramente menor, o que não era esperado.
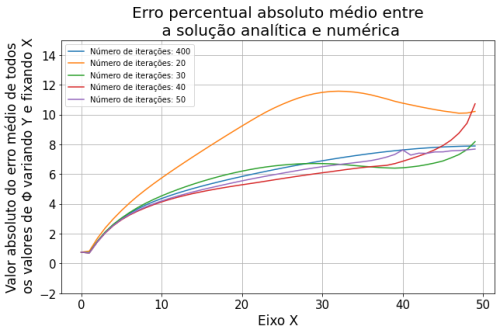
Resultados do Método de Superrelaxação
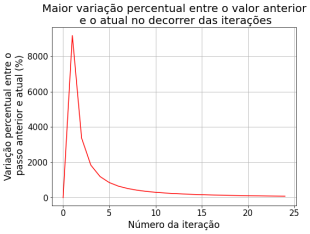
A implementação numérica do Método de Superrelaxação atingiu o mesmo comportamento que a solução analítica. Este método obteve a maior variação, chegando à 25.000% nas primeiras 10 iterações. Porém, a partir do 90º passo a variação já era menor que 0.1%, o que demonstra ser o método mais rápido para convergir à uma solução estacionária.
Um fenômeno não esperado para este método que pudemos observar foram picos de variação nas iterações múltiplas de 50, que é valor do tamanho do nosso plano XY.
Observamos também o fato do erro apresentar valores menores para um número de iterações menores, porém para um valor de passos muito menor do que os outros métodos, abaixo de 50 iterações, que já notamos que já obtivemos a solução da Equação de Laplace.
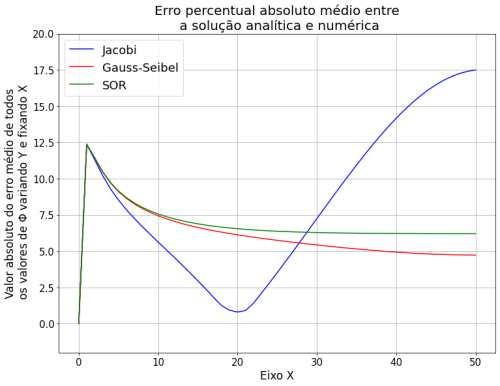
Por fim, analisamos a precisão de cada método e é possível observar que o Método de Gauss-Seidel apresentou os menores erros, porém necessita mais iterações comparado ao método SOR, que tem um erro ligeiramente maior, porém é cerca de 20 vezes mais rápido..
Problema do Dipolo Elétrico
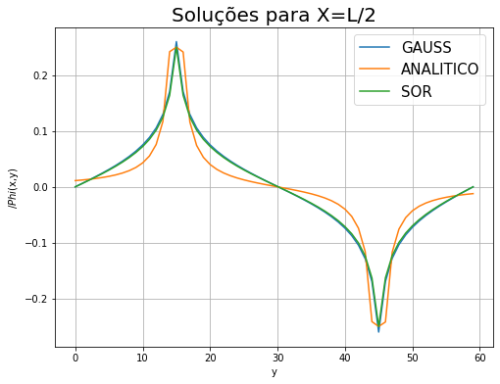
Observando os gráficos dos resultados acima é possível concluir que os métodos implementados atingiram o mesmo comportamento da solução analítica.
No gráfico acima observamos que apesar de alcançar a solução estacionária, a equação de iteração não consegue alcança com precisão a equação analítica.
Por fim, um ponto que gostaríamos de ressaltar é a facilidade de modelar um problema complexo de eletroestática com estas implementações. Muitas vezes é difícil de chegar à uma equação analítica para uma densidade de carga complexa, porém em código é possível com algumas restrições modelar problemas com geometrias bem específicas.
Link para Códigos
Fizemos no ambiente Colab em .ipynb, segue link do github:[1]
Referências
- ↑ 1,0 1,1 GRIFFITHS, David J. Introduction to electrodynamics. New Jersey: Prentice Hall, 1962.
- ↑ GARCIA, Alejandro L. Numerical methods for physics. Englewood Cliffs, NJ: Prentice Hall, 2000.
- ↑ Numerical solution of partial differential equations, Dr. Louise Olsen-Kettle. The University of Queensland School of Earth Sciences Centre for Geoscience Computing.
- ↑ SAYAMA, Hiroki. Introduction to the modeling and analysis of complex systems. Open SUNY Textbooks, 2015.