Modelo de Keller-Segel para relação população-economia

Grupo: Leonardo Barcelos, Luana Bianchi e Rubens Borrasca

O objetivo deste trabalho é implementar o modelo de Keller-Segel, que originalmente descreve chemotaxis: movimento de organismo em direção ou contra algum sinal químico, para um sistema englobando população e atividade econômica. O método computacional utilizado para resolver o problema e implementar o modelo foi o FTCS (Forward Time Centered Space).

Modelo de Keller-Segel

Proposto por Evelyn Fox Keller, física norte-americana, e Lee Aaron Segel, matemático também norte-americano, o modelo de Keller-Segel foi historicamente utilizado para descrever o movimento de bactérias. Introduzido primeiramente em 1970 para descrever a agregação de uma espécie de bolor limoso (ou slime mold) ameboide, Dictyostelium discoideum, o modelo se tornou um dos mais usados nos estudos biológicos-matemáticos. As células deste slime mold se comportam como amoebas individuais, e se alimentam de bactérias, mas quando a quantidade de comida fica pequena, elas se difundem pelo espaço e então se agregam em formato mais alongado, como o formato das lesmas, para uma migração de longa distância. Keller e Segel desenvolveram um modelo matemático para o processo de agregação, em que a chemotaxis tem papel crítico na auto-ormanização das células.

Baseados no que já era conhecido sobre esses organismos, Keller e Segel utilizaram as seguintes premissas:

• As células estão inicialmente distribuídas sobre o espaço de maneira mais ou menos homogênea, com algumas flutuações aleatótias;
• As células apresentam chemotaxis em direção ao sinal químico denominado cAMP (cyclic adenosine monophosphate);
• As células produzem moléculas cAMP;
• As células e as moléculas cAMP difundem pelo espaço;
• As células não morrem e não se dividem

De forma simplificada, ocultando alguns detalhes biológicos mais complicados a equação de Keller-Segel é a seguinte:

${\frac {\partial a}{\partial t}}=\mu \nabla ^{2}a-\chi \nabla \cdot (a\nabla c)$

${\frac {\partial c}{\partial t}}=D\nabla ^{2}c+fa-kc$

em que $a$ e $c$ são respectivamente as variáveis de estado para a concentração de células e a concentração de cMAP. $\mu$ é o parâmetro de mobilidade das células, $\chi$ é o parâmetro da chemotaxis celular, $D$ é a constante de difusão das moléculas cAMP, $f$ é a taxa de secreção de cMAP pelas células, e $k$ é a taxa de decaimento das moléculas cMAP.

Aplicação população-economia

De forma parecida com as premissas de Keller e Segel, os seguintes pontos são assumidos para modelar a relação entre a população e a atividade econômica:

• A população não cresce e não decresce ao longo do tempo;
• A economia é ativada por existir mais pessoas em uma região;
• Sem pessoas a atividade econômica diminui;
• População e atividade econômica difundem gradualmente;
• As pessoas são atraídas por regiões com maior atividade econômica

Traduzindo estes pontos em equações matemáticas, se obtêm as seguintes equações:

${\frac {\partial p}{\partial t}}=D_{p}\nabla ^{2}p-\gamma \nabla \cdot (p\nabla m)$

${\frac {\partial m}{\partial t}}=D_{m}\nabla ^{2}m+\alpha p-\beta m$

em que $p$ representa a população e $m$ a atividade econômica. $\alpha$ é a constante que determina a taxa de produção de atividade econômica per capita, $\beta$ é a constante da taxa de decaimento da atividade econômica, $D_{p}$ e $D_{m}$ são as constantes de difusão da população e da economia respectivamente, e $\gamma$ é a constante que afeta a velocidade média do movimento da população.

Comparando o sistema obtido com o problema original de Keller-Segel, percebe-se que se trocarmos células por pessoas e cMAP por atividade econômica os problemas ficam iguais, e até se poderia denominar como moneytaxis a migração das pessoas em direção a atividade econômica, como a chemotaxis descreve o movimento das células em direção ao cAMP.

Método FTCS

O FTCS (Forward Time Centered Space, em tradução livre significa "avançado no tempo, centrado no espaço), é um método de discretização de Equações Diferenciais Parciais(EDP). Para a derivada temporal teremos,

${\frac {\partial f}{\partial t}}\rightarrow {\frac {f^{n+1}-f^{n}}{\Delta t}}$

e para a parte espacial,

${\frac {\partial ^{2}f}{\partial s^{2}}}\rightarrow {\frac {f_{i-1}-2f_{i}+f_{i+1}}{(\Delta s)^{2}}}$

onde $s$ é uma variável espacial qualquer $(x,y,z,...)$ e $t$ é o tempo.

Discretização do Modelo de Keller-Segel em 1D

Em 1D o sistema de equações diferenciais parciais será:

${\frac {\partial p}{\partial t}}=D_{p}{\frac {\partial ^{2}p}{\partial x^{2}}}-\gamma \left[{\frac {\partial p}{\partial x}}{\frac {\partial m}{\partial x}}+p{\frac {\partial ^{2}m}{\partial x^{2}}}\right]$

${\frac {\partial m}{\partial t}}=D_{m}{\frac {\partial ^{2}m}{\partial x^{2}}}+\alpha p-\beta m$

Agora utilizando a discretização FTCS teremos:

${\frac {p_{i}^{n+1}-p_{i}^{n}}{\Delta t}}={\frac {D_{p}}{(\Delta x)^{2}}}\left[p_{i-1}^{n}-2p_{i}^{n}+p_{i+1}^{n}\right]-{\frac {\gamma }{(\Delta x)^{2}}}\left[(p_{i+1}^{n}-p_{i}^{n})(m_{i+1}^{n}-m_{i}^{n})+p_{i}^{n}(m_{i-1}^{n}-2m_{i}^{n}+m_{i+1}^{n})\right]$

${\frac {m_{i}^{n+1}-m_{i}^{n}}{\Delta t}}={\frac {D_{m}}{(\Delta x)^{2}}}\left[m_{i-1}^{n}-2m_{i}^{n}+m_{i+1}^{n}\right]+\alpha p_{i}^{n}-\beta m_{i}^{n}$

onde o sub-índice $i$ se refere à coordenada $x$; e o superíndice $n$ se refere ao tempo. Reorganizando as equações e agrupando alguns termos teremos:

$p_{i}^{n+1}=p_{i}^{n}\left[1-2K_{1}-K_{2}\left(m_{i-1}^{n}-m_{i}^{n}\right)\right]+K_{1}\left[p_{i-1}^{n}+p_{i+1}^{n}\right]-K_{2}\left[p_{i+1}^{n}(m_{i+1}^{n}-m_{i}^{n})\right]$

$m_{i}^{n+1}=m_{i}^{n}\left[1-K_{3}-\lambda \right]+K_{3}\left[m_{i-1}^{n}+m_{i+1}^{n}\right]+Vp_{i}^{n}$

onde os termos agrupados são: $K_{1}={\frac {D_{p}\Delta t}{(\Delta x)^{2}}}$ , $K_{2}={\frac {\gamma \Delta t}{(\Delta x)^{2}}}$ , $K_{3}={\frac {D_{m}\Delta t}{(\Delta x)^{2}}}$ , $V=\alpha \Delta t$ , $\lambda =\beta \Delta t$

Discretização do Modelo de Keller-Segel em 2D

Em 2D o sistema de equações diferenciais parciais será:

${\frac {\partial p}{\partial t}}=D_{p}\left[{\frac {\partial ^{2}p}{\partial x^{2}}}+{\frac {\partial ^{2}p}{\partial y^{2}}}\right]-\gamma \left[{\frac {\partial p}{\partial x}}{\frac {\partial m}{\partial x}}+{\frac {\partial p}{\partial y}}{\frac {\partial m}{\partial y}}+p\left({\frac {\partial ^{2}m}{\partial x^{2}}}+{\frac {\partial ^{2}m}{\partial y^{2}}}\right)\right]$

${\frac {\partial m}{\partial t}}=D_{m}\left[{\frac {\partial ^{2}m}{\partial x^{2}}}+{\frac {\partial ^{2}m}{\partial y^{2}}}\right]+\alpha p-\beta m$

Agora utilizando a discretização FTCS e assumindo que $\Delta x=\Delta y=\Delta s$ teremos:

${\frac {p_{i,j}^{n+1}-p_{i,j}^{n}}{\Delta t}}={\frac {D_{p}}{(\Delta s)^{2}}}\left[(p_{i-1,j}^{n}-2p_{i,j}^{n}+p_{i+1,j}^{n})+(p_{i,j-1}^{n}-2p_{i,j}^{n}+p_{i,j+1}^{n})\right]-{\frac {\gamma }{(\Delta s)^{2}}}\left[(p_{i+1,j}^{n}-p_{i,j}^{n})(m_{i+1,j}^{n}-m_{i,j}^{n})+(p_{i,j+1}^{n}-p_{i,j}^{n})(m_{i,j+1}^{n}-m_{i,j}^{n})+p_{i,j}^{n}\left((m_{i-1,j}^{n}-2m_{i,j}^{n}+m_{i+1,j}^{n})+(m_{i,j-1}^{n}-2m_{i,j}^{n}+m_{i,j+1}^{n})\right)\right]$

${\frac {m_{i,j}^{n+1}-m_{i,j}^{n}}{\Delta t}}={\frac {D_{m}}{(\Delta s)^{2}}}\left[(m_{i-1,j}^{n}-2m_{i,j}^{n}+m_{i+1,j}^{n})+(m_{i,j-1}^{n}-2m_{i,j}^{n}+m_{i,j+1}^{n})\right]+\alpha p_{i,j}^{n}-\beta m_{i,j}^{n}$

onde os sub-índices $i$ e $j$ se referem às coordenadas $x$ e $y$ respectivamente; e o superíndice $n$ se refere ao tempo. Reorganizando as equações e agrupando alguns termos teremos:

$p_{i,j}^{n+1}=p_{i,j}^{n}\left[1-4K_{1}-K_{2}\left(m_{i-1,j}^{n}-2m_{1,j}^{n}+m_{i,j-1}^{n}\right)\right]+K_{1}\left[p_{i-1,j}^{n}+p_{i,j-1}^{n}+p_{i+1,j}^{n}+p_{i,j+1}^{n}\right]-K_{2}\left[p_{i+1,j}^{n}(m_{i+1,j}^{n}-m_{i,j}^{n})+p_{i,j+1}^{n}(m_{i,j+1}^{n}-m_{i,j}^{n})\right]$

$m_{i,j}^{n+1}=m_{i,j}^{n}\left[1-4K_{3}-\lambda \right]+K_{3}\left[m_{i-1,j}^{n}+m_{i,j-1}^{n}+m_{i+1,j}^{n}+m_{i,j+1}^{n}\right]+Vp_{i,j}^{n}$

Resultados

1D

Com o intuito de testar melhor a equação e suas consequências, os resultados foram divididos em várias simulações diferentes.

Para todas as simulações realizadas, exceto onde indicado, os parâmetros utilizados foram os seguintes:

$N=100$

$dx=1$

$dt=0.3$

$D_{m}=1$

$D_{p}=1$

$\gamma =1$

$\alpha =1$

$\beta =1$

Além disso, foram utilizadas condições periódicas de contorno (PBC) para a solução das equações diferenciais parciais. Deste modo, pode-se pensar no eixo x como uma "rosquinha", onde, considerando um sistema de tamanho $N$, os pontos $x=0$ e $x=N$ estão conectados.

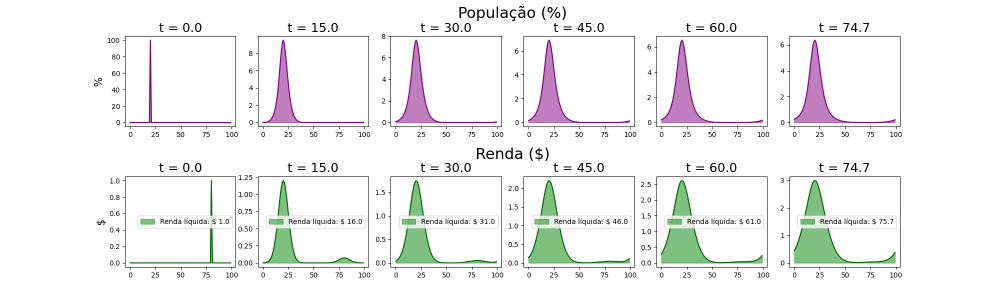
População e Dinheiro em pontos separados

Para esta simulação, considera-se que no tempo 0, toda a população está concentrada em 1 ponto $x={\mathcal {C}}_{1}$, enquanto todo o dinheiro está em um outro ponto, distante deste, $x={\mathcal {C}}_{2}$. Deste modo, temos as seguintes equações para as condições iniciais:

$p(x,t=0)=\left\{{\begin{array}{lc}1,\quad {\text{p/}}\quad x={\mathcal {C}}_{1},{\mathcal {C}}_{1}\in [0,N]\\0,\quad {\text{caso contrario}}\end{array}}\right.$

$m(x,t=0)=\left\{{\begin{array}{lc}1,\quad {\text{p/}}\quad x={\mathcal {C}}_{2},{\mathcal {C}}_{2}\in [0,N],{\mathcal {C}}_{2}\neq {\mathcal {C}}_{1}\\0,\quad {\text{caso contrario}}\end{array}}\right.$

Na figura abaixo, consegue-se observar o resultado da construção do sistema desta maneira:

Resultados da simulação para o caso de população e dinheiro em pontos separados e distantes na malha

Com toda a população concentrada em 1 ponto ($x=20$), a atividade econômica cresce consideravelmente neste intervalo ao longo do tempo. Em contrapartida, o local que continha todo o dinheiro no começo da simulação ($x=80$), em pouco tempo tem a sua renda líquida migrada para onde tem uma densidade populacional maior. Essa tendência indica, portanto, que o sistema é construído de tal forma que a atração da população por regiões de alta renda líquida é menor que a atração do sistema monetário de seguir para pontos de alta densidade populacional.

Além disso, outra observação interessante é que nota-se para $t\rightarrow \infty$ uma tendência inerente da densidade populacional em seguir uma distribuição de shape gaussiano sob a malha. Considerando que a equação que define o movimento populacional com o tempo contém um termo difusivo, e que a solução para uma difusão simples em 1 dimensão também assume um shape gaussiano, este resultado faz sentido. Mas uma coisa interessante é que, depois de se desfazer de seu formato inicial, o total de dinheiro sob a malha tende a seguir a distribuição populacional, porém com um desvio padrão maior (maior abertura na Gaussiana). Essa observação indica que, para centros econômicos (regiões com alto $m$) a tendência é que suas periferias também possuam valores altos de renda, apesar da população consideravelmente menor. Além disso, para regiões fora do contorno de centros econômicos (distância maior do que 3 vezes o desvio padrão da gaussiana) a atividade econômica é basicamente nula, assim como a densidade populacional. Este último fato descreve de forma genérica e simplista o comportamento atual observado em metrópoles nos dias de hoje: uma cidade grande possui alto número de habitantes, alta renda, seus contornos também apresentam atividade econômica forte (porém menor que o centro), mas para um raio suficientemente grande, tanto dinheiro quanto população caem exponencialmente.

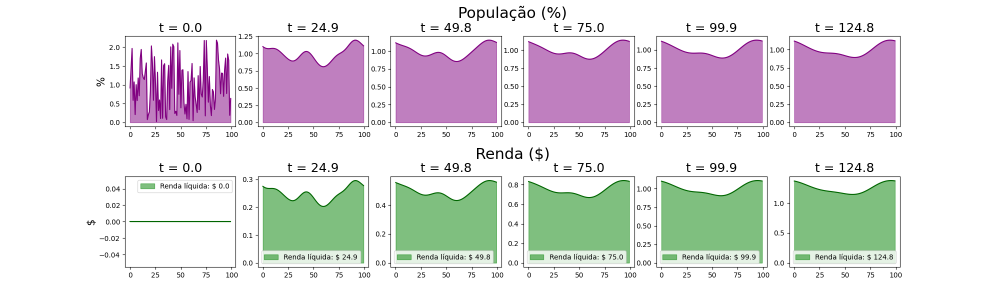
População uniforme e sem dinheiro no sistema para t = 0

Nesta simulação, considera-se que, para t=0, não há dinheiro sob a malha. Deste modo, a equação que descreve o dinheiro no sistema ao longo do tempo pode ser escrita como:

$m(x,t=0)=0,\forall x\in [0,N]$

Além disso, a população é iniciada de forma aleatória sob a malha. Deste modo, não há tendência inicial à formação de centros com alta densidade de população.

Esta forma inicial da população se assemelha muito à proposição inicial que Keller-Segel fizeram para um sistema celular, como descrito acima. Na prática, temos uma concentração homogênea com pequenas flutuações ao longo do eixo.

Resultados da simulação para o caso de m(x,t=0)=0, e população iniciada aleatoriamente.

Na imagem acima, para t = 0 (início da simulação) compreende-se melhor as condições iniciais do sistema. Enquanto que a população, aleatoriamente distribuída sob o eixo x, se assemelha a um ruído branco, o dinheiro não existe na malha.

Na segunda coluna de imagens, nota-se um ponto interessante: a formação de clusters de população (e consequentemente, de dinheiro). Estes clusters são, na verdade, picos que aparecem no gráfico de p(x,t), e indicam alta concentração da população em pontos específicos. Além dos picos claramente visíveis (um deles próximo a x=50, e outro próximo a x=90) pode-se enxergar, também, sub-picos nas bases destes picos de população. Para t=24.9 e dt=0.3, deduz-se que o sistema, nesta representação, havia passado por 83 iterações até então, o que indica que, durante estas 83 iterações, haviam mais clusters de população em tempos passados, menores porém definidos. E estes "mini-clusters" se agruparam até formar os 2 picos que vemos.

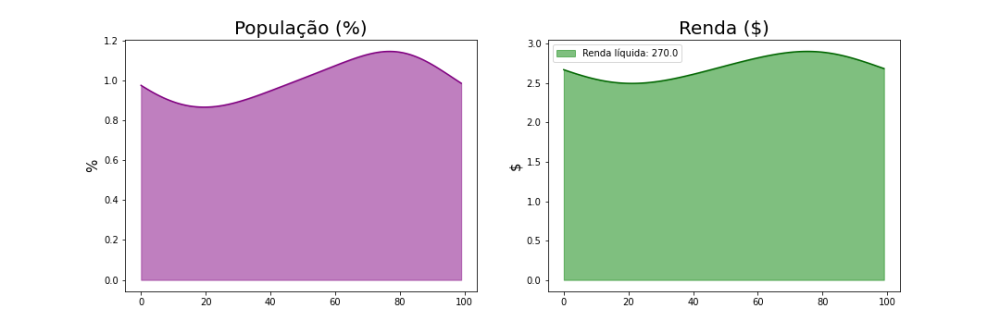
Com o passar do tempo na simulação, nota-se que o comportamento continua, de modo que para a última coluna de figuras é visível que apenas 1 dos picos iniciais se manteve, enquanto o outro foi praticamente inteiro "engolido" pela cauda do maior. Este comportamento de formação de 1 único cluster de população, com shape gaussiano, já havia sido observado na simulação anterior, para $t$ suficientemente grande.

Simulação do mesmo sistema anterior, para t suficientemente grande (t = 270 neste caso) a ponto de chegar em um estado próximo ao equilíbrio, onde as funções que descrevem população e renda do sistema praticamente não se alteram mais com o tempo.

A figura acima mostra o que acontece caso deixemos o mesmo sistema apresentado antes evoluir até um estado de equilíbrio, onde não há alterações para a população ou renda do sistema. Neste caso, observa-se com mais clareza uma curva de shape gaussiano, em localização bem próxima àquela que vimos para t=124.8 na figura anterior, tanto para a distribuição da população quanto da renda. E mais uma vez, mesmo que não muito perceptível pois as 2 curvas apresentadas são bem largas, o desvio padrão da curva que descreve a renda aparenta ser maior que o desvio padrão da curva que descreve a população.

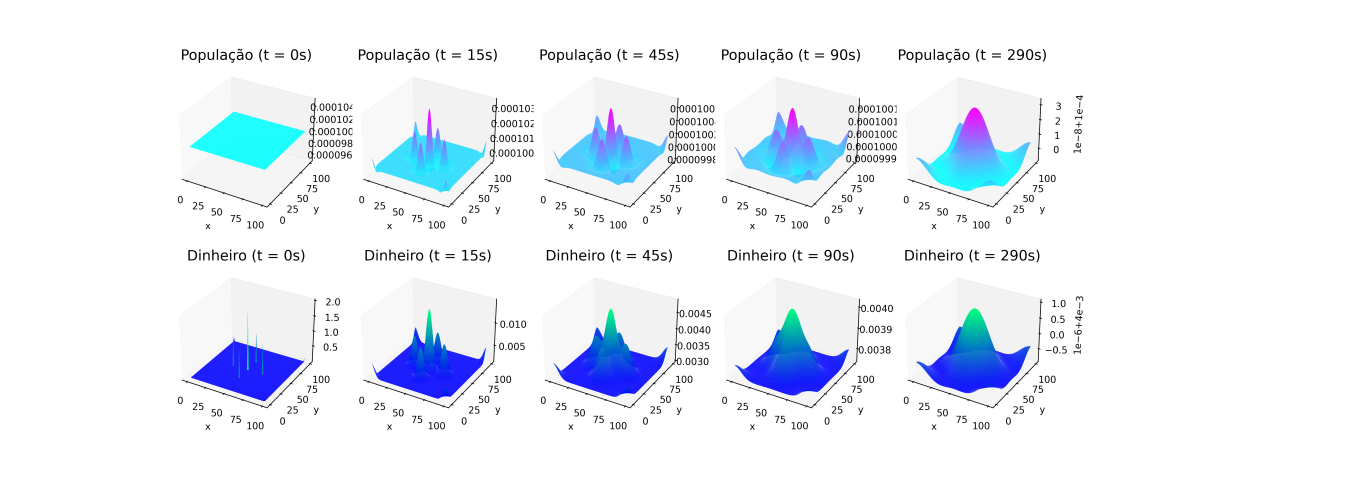
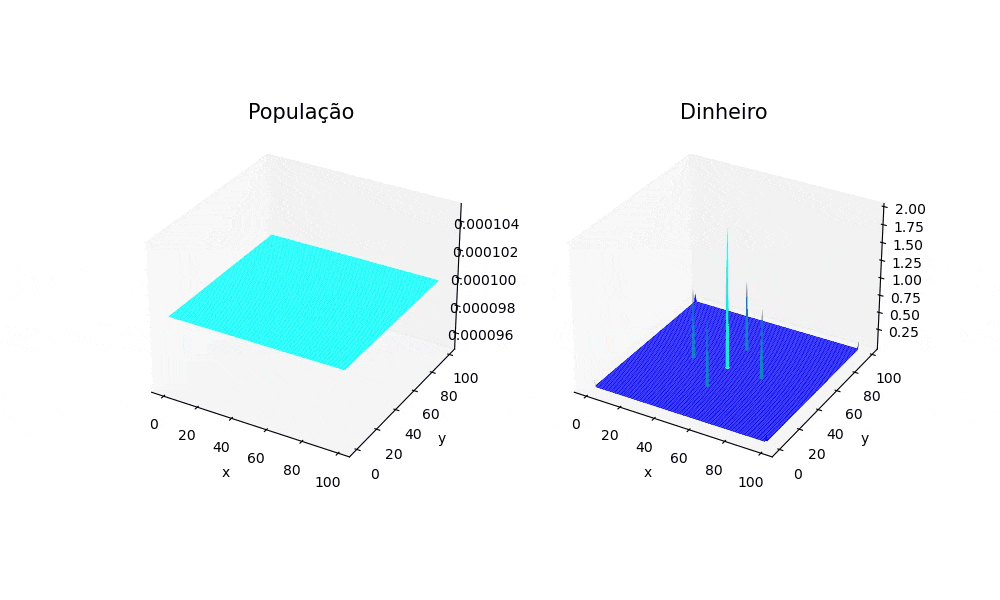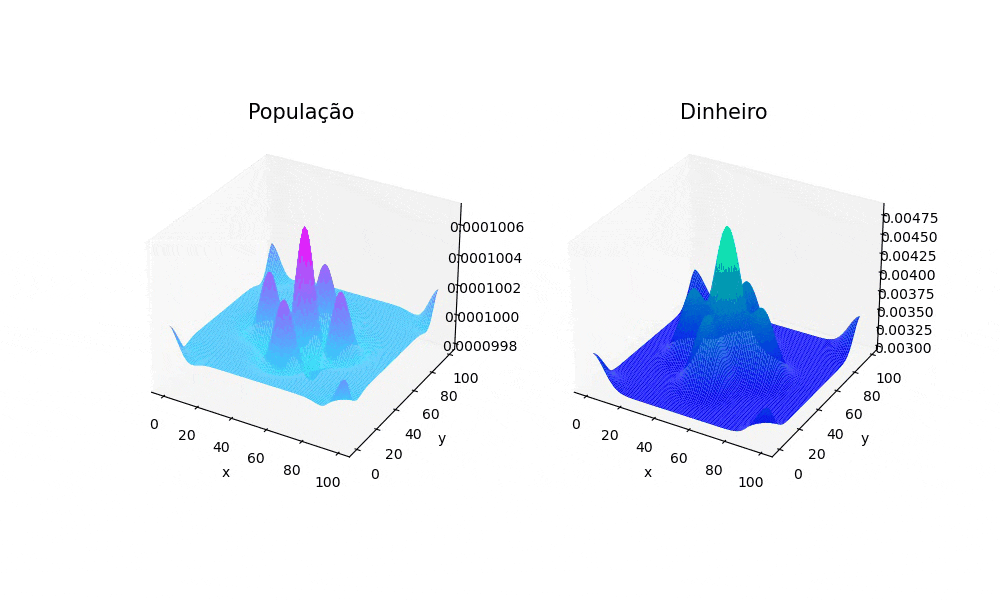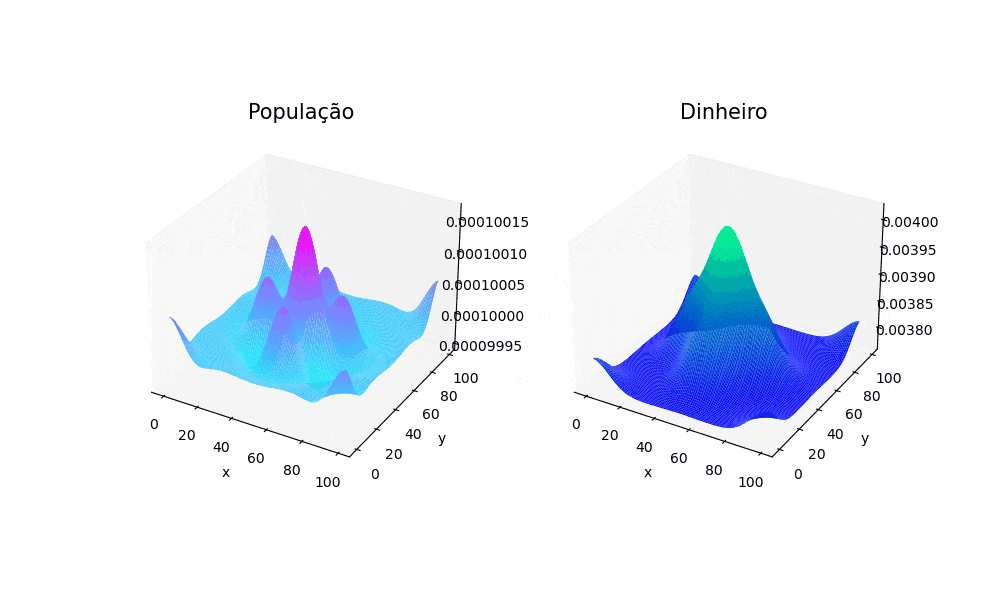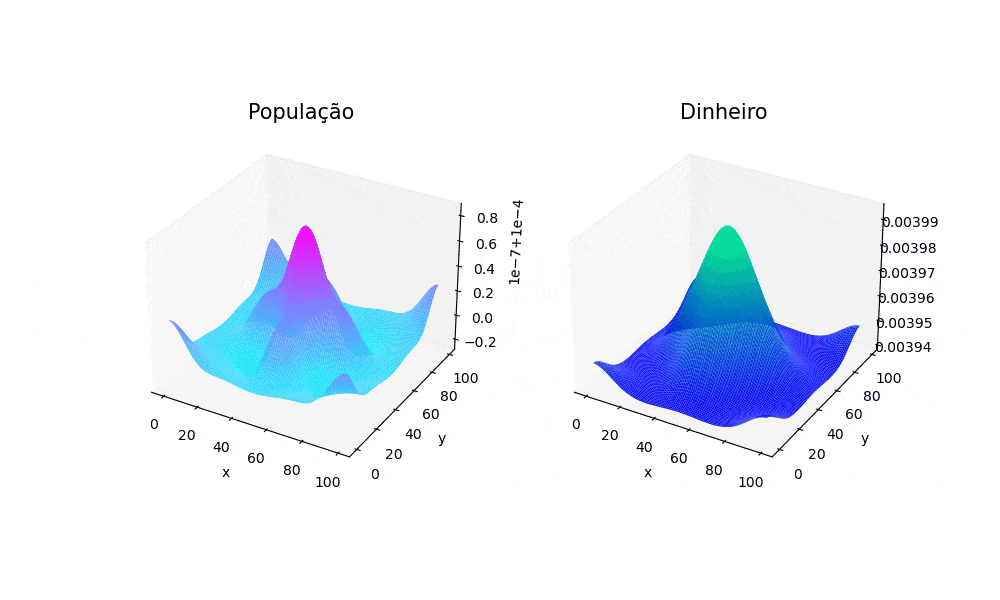
2D

Para o caso em duas dimensões, foi utilizada uma distribuição populacional uniforme em todo o espaço. Já a distribuição econômica, no instante t=0 começou da seguinte forma: Em cada canto do espaço foi atribuído um valor de 0.125, no centro 0.2 e ao redor do centro em 4 pontos 1. A seguir, é confirmado um comportamento que foi observado no caso unidimensional, em que os picos concentrados, após a evolução do sistema, tomam a forma de gaussianas. É possível notar também que a população tende a "clusterizar" em torno dos locais em que a atividade econômica tinha valores altos no início da simulação. Isso se deve principalmente ao termo que é influenciado pela constante $\gamma$ do sistema de EDPs que modela o sistema.

Evolução da atividade econômica e da população para população inicial uniformemente distribuída

A seguir, foi gerada uma animação com a evolução do sistema até a estabilização da atividade econômica. A estabilidade da atividade econômica foi entendida como Falhou ao verificar gramática (erro de sintaxe): {\displaystyle max(f^{t+10}_{i,j} − f^t_{i,j}) \leqslant \epislon} , onde $\epsilon$ é usado para definir o número de casas decimais, e $S$ é o espaço onde o dinheiro está distribuído. Para este caso $\epsilon =1\times 10^{-9}$

Animação da evolução do sistema

Os parâmetros utilizados para gerar as imagens foram os seguintes: $L=100$, $ds=1$, $dt=0.3$, $D_{m}=0.5$, $D_{p}=0.5$, $\alpha =1.2$, $\beta =0.03$, $\gamma =1$

Referências

Sayama

Scherrer

[1]