DM: um primeiro programa
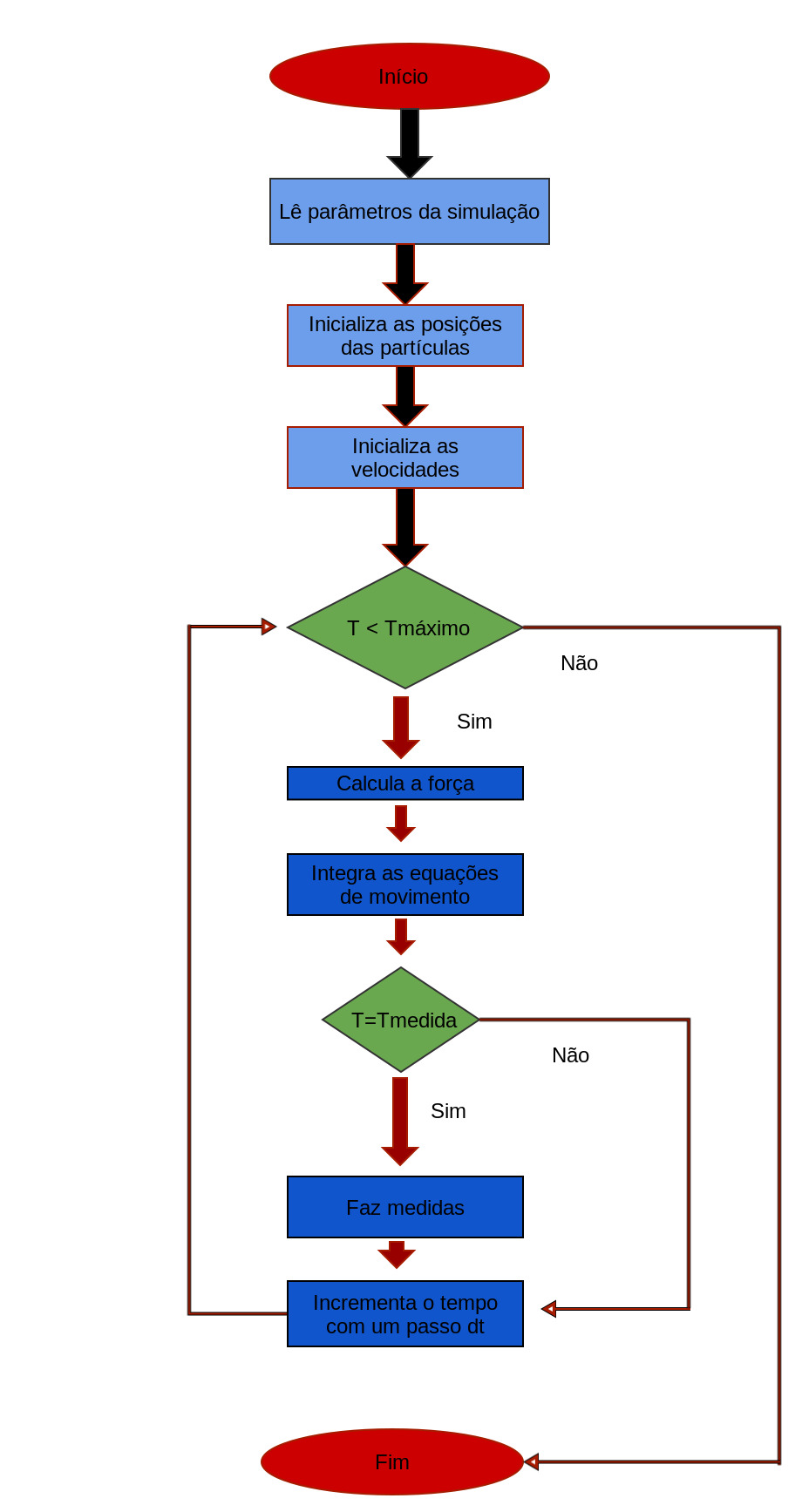
[EM CONSTRUÇÃO] Aqui mostraremos o passo a passo de como montar o primeiro programa para simulação de dinâmica molecular. A linguagem de programação utilizada será o C. Como um primeiro esboço, o programa pode ser organizado como mostra o fluxograma abaixo. Posteriormente, introduziremos partes do código comentando cada etapa. Para o leitor mais familiarizado com DM, ao final da página há o programa completo sem comentários.
A ideia básica da simulação pode ser entendida como: Leitura dos parâmetros da simulação, inicialização das posições das partículas, inicialização das velocidades das partículas, laço temporal onde se calcula a força, integra-se as equações de movimento e, de tempos em tempos, medidas são realizadas.
Abaixo introduzimos partes do código onde começamos declarando as bibliotecas standard utilizadas do C
#include<stdio.h> #include<stdlib.h> #include<math.h>
Está parte é reservada para declarações de constantes que definem os parâmetros da simulação. As constantes podem ser definidas utilizando-se das diretivas de compilação do C através do comando "#define" ou podem ser lidas a partir de um arquivo externo chamado pelo programa. A vantagem do segundo método é que o programa só precisará ser compilado uma única vez para diferentes condições iniciais. Porém, por simplicidade e clareza, optaremos pelo primeiro caso.
#define Nx 16 #define Ny 16 #define Np (Nx*Ny) #define Lx 16 #define Ly 16 #define Rc 4 #define Rc2 (Rc*Rc) #define T 1. #define dt 0.01 #define transient 5. #define total_time 10. #define measure 0.1 #define samples ((total_time-transient)/measure)
representam, respectivamente, o número de partículas nas direções .
representam, respectivamente, o tamanho da rede nas direções .
número total de partículas
define o intervalo de tempo de integração na simulação.
é o raio de corte acima do qual o cálculo da força é desconsiderado.
é o tempo absoluto da simulação.
é o tempo que esperamos até o sistema supostamente equilibrar e, então, começarmos a fazer medidas.
define o intervalo de tempo entre as medições.
nos dá o número total de medidas que serão realizadas
Conforme o programa é construído, novas constantes podem eventualmente aparecer à medida que novas funções são implementadas. Abaixo declaramos as funções essenciais ao programa, onde cada uma delas será detalhadamente explicada no decorrer da implementação.
void initialize_positions(double *xx, double *yy ) ; void initialize_velocities(double *vx, double *vy ) ; void compute_forces( double *ffx, double *ffy, double *xx, double *yy, double *eenergia ) ; void integrate_EqMotion( double *fx, double *fy, double *xx, double *yy, double *xxp, double *yyp, double eenergia, double *energy_pp, double *vxm ) ;
A seguir introduzimos a função principal
void main(void)
{
FILE *file1,*file2;
file1=fopen("energy.dat","w");
file2=fopen("trajectories.dat","w");
unsigned i;
double *x,*y,*xo,*yo,*vx,*vy,*Fx,*Fy,Ep,Ec,Vxm=0.,t;
size_t size=N*sizeof(double);
x= (double*)malloc(size);
y= (double*)malloc(size);
xo=(double*)malloc(size);
yo=(double*)malloc(size);
vx=(double*)malloc(size);
vy=(double*)malloc(size);
Fx=(double*)malloc(size);
Fy=(double*)malloc(size);
Acima são declaradas todas as variáveis essenciais ao programa, assim como a alocação de memória para os vetores como posição, velocidade, força, etc. Com os vetores alocados, podemos agora inicializar as velocidades e posições das partículas na rede
initialize_velocities(vx,vy); initialize_positions(x,y,xo,yo,vx,vy);
Abaixo é mostrada a parte principal do programa, o loop sobre o tempo. A cada passo de tempo, a rotina calcula a força e a energia potencial das partículas a partir de suas posições, na sequência, a rotina atualiza as posições das partículas. O em imprime no arquivo "trajectories.dat" as posições e velocidades de todas as partículas no instante . No testamos se o tempo total é maior que o tempo de equilíbrio e se a medida deve ser feita, caso seja, no arquivo "energy.dat" imprimiremos, respectivamente, o tempo, energia cinética, energia potencial e a soma das duas últimas.
for(t=0.;t<total_time;t+=dt)
{
compute_forces(Fx,Fy,x,y,&Ep);
integrate_EqMotion(Fx,Fy,x,y,xo,yo,&Ec,&Vxm);
for(i=0;i<N;i++)fprintf(file2,"%lf %lf %lf %lf\n",x[i],y[i],vx[i],vy[i]);
fflush(file2);
rewind(file2);
if( t>transient && (1.-fmod(t/measure,1.) )<0.00001 )
{
fprintf(file1,"%lf %lf %lf %lf\n",t,Ec,Ep,Ec+Ep);
fflush(file1);
}
}
fclose(file1);
fclose(file2);
free(x);
free(y);
free(xo);
free(yo);
free(vx);
free(vy);
free(Fx);
free(Fy);
}
void initialize_positions( double *xx, double *yy ) {
int i ;
double deltax, deltay;
deltax = (double)Lx/Nx; deltay = (double)Ly/Ny;
for(i = 0; i < NP; i++)
{
xx[i] = (i%Nx)*deltax ;
yy[i] = (i/Ny)*deltay ;
// printf("%lf %lf %d \n", xx[i], yy[i], i);
}
}
void initialize_velocities(double *vx, double *vy ) {
int i ; double vcmx, vcmy, v2, fs;
vcmx=0.0; vcmy=0.0; v2=0.0;
for(i = 0; i < NP; i++)
{
vx[i] = (double)rand()/RAND_MAX ;
vy[i] = (double)rand()/RAND_MAX ;
vcmx += vx[i]; vcmy += vy[i];
v2 += vx[i]*vx[i] + vy[i]*vy[i] ; // kinetic energy
}
vcmx /= NP ; vcmy /= NP ; v2 /= NP;
fs=sqrt(2*TEMP/v2) ; // fator de escala -- escolhe uma dada temp T e computa isto : SE escolher uma dist maxwelliana, isto nao eh necessario (me parece)
// set the velocity center of mass to zero (linear momentum of the system is zero)
// and set its value in such a way that \sum m_i v^2 = Kb T for each degree of freedom
for(i = 0; i < NP; i++)
{ vx[i] = (vx[i] - vcmx)*fs ; vy[i] = (vy[i]-vcmy)*fs ; }
}
// fx = -dV/dx = -(x/r) (dV/dr) // fx= 48x/r² (1/r^12 - 1/r^6) -- LJ in reduced Units void compute_forces( double *ffx, double *ffy, double *xx, double *yy, double *eenergia ) {
int i, j;
double x1, y1, x2, y2,dxx, dyy, r2, r2i, r6, ff, energia=0.0 ;
for( i=0; i < NP; i++ )
{ ffx[i] = 0.0; ffy[i] = 0.0; }
for( i=0; i < NP; i++ )
{
x1 = xx[i]; y1 = yy[i];
for( j=i+1; j < NP; j++ )
{ x2 = xx[j]; y2 = yy[j];
dxx = x1 - x2; // compute the distance between particles taking into account the periodic boundary conditions dxx = fmod(dxx, Lx); dxx=dxx-rint(dxx/Lx)*Lx ; //note: rint(arg) : rounds its argument to the nearest whole number
dyy = y1 - y2; dyy = fmod(dyy, Ly); dyy=dyy-rint(dyy/Ly)*Ly ;
r2 = dxx*dxx + dyy*dyy ; if(r2<RC2) // rc2: critical value or r { r2i = 1/r2 ; r6 = r2i*r2i*r2i; ff = 48*r2i*r6*(r6-0.5); // LJ potential integrated ffx[i] += ff* dxx ; ffy[i] += ff* dyy ; // update forces ffx[j] -= ff* dxx ; ffy[j] -= ff* dyy ; energia += 4*r6*(r6-1) ; // compute energy } }
} *eenergia=energia;
}
void integrate_EqMotion( double *ffx, double *ffy, double *xx, double *yy, double *xxp, double *yyp, double eenergia, double *energy_pp, double *vxm )
{
int i; double xp, yp, vxi, vyi, vcmx, vcmy, v2, temp ;
vcmx=0.0; vcmy=0.0; v2=0.0;
for(i = 0; i < NP; i++)
{
xp = 2*xx[i] - xxp[i] + deltat2 * ffx[i] ;
yp = 2*yy[i] - yyp[i] + deltat2 * ffy[i] ;
vxi = (xp - xx[i]) / (2*deltat);
vyi = (yp - yy[i]) / (2*deltat);
vcmx += vxi; vcmy += vyi; // to monitor the average velocity
v2 += vxi*vxi + vyi*vyi ; // kinetic energy
xxp[i] = xx[i] ; yyp[i] = yy[i] ; // update the "previous position"
yyp[i] = yy[i] ;
xx[i] = xp; // update the positions in a current time
yy[i] = yp;
}
temp=v2/(2*NP) ; // kbT = < m*v^2 > per degree of freedom
*energy_pp=(eenergia + 0.5*v2)/NP; // energia total = ( U + K ) -- energy per particle =energia/NP
*vxm = vcmx /NP ;
}