Ressonância Estocástica

Introdução

A ressonância estocástica é o fenômeno em sistemas não-lineares em que sinais fracos podem ser amplificados e otimizados por um ruído branco, sendo o efeito encontrado em função do nível de ruído e de características do sistema e do sinal. [1]

Linear vs não linear:

A concepção convencional é de que ruídos deterioram um sinal, oposto do que acontece na Ressonância Estocástica (RE). Um ponto chave para essa discrepância é a distinção entre sistemas lineares e não-lineares. Em termos gerais, em sistemas lineares, a combinação de duas entradas resulta em uma saída equivalente à combinação das saídas que o sistema daria para cada entrada em separado. [2] Ou seja, para uma função f linear, se f(x) = y e f(a) = b, então f(x+a) = y+b. Sistemas não-lineares, por outro lado, são todos aqueles que não são lineares. [2] É de se esperar que em sistemas lineares a adição de ruído possa apenas degradar ou mascarar um sinal inicial (o exemplo mais simples é a soma direta do ruído ao sinal). A RE é portanto um processo próprio de sistemas não-lineares. A não-linearidade, contudo, não é condição suficiente para que o fenômeno ocorra.

Condições para RE: Em geral, são condições necessárias para RE [1]:

- Barreira/Limiar: um “obstáculo” à percepção de um sinal ou ao acontecimento de um evento. Um exemplo simples seria o efeito de “delta” em: f(x) = x, se x > delta; f(x) = 0, se x <= delta [ex]

- Sinal Fraco Coerente: um sinal (entrada) que obedeça certo padrão e não seja, em geral, capaz de “superar” a barreira ou limiar associado ao sistema. O sentido físico dessa “superação” depende do sistema. Seguindo o exemplo anterior, essa condição seria satisfeita se x <= delta fosse verdade para todos x, por exemplo.

- Fonte de Ruído Não Correlacionado (ou “ruído branco”): um sinal estocástico não-autocorrelacionado, de média zero, que não carrega informação se não por sua intensidade, que é a mesma para todas as frequências (e, no caso de um ruído branco gaussiano, está ligada ao desvio padrão).

Breve Apanhado Histórico

- Primeiras Verificações Experimentais: Em tradução livre de [intro do 1]: ”Uma primeira verificação experimental do fenômeno de ressonância estocástica foi obtida por Fauve e Heslot (1983), que estudaram como a linha espectral de um gatilho de Schmitt dependia do ruído. O campo permaneceu então meio adormecido até a era moderna da ressonância estocástica ser introduzida por um experimento chave em um ring laser biestável (McNamara, Wiesenfeld, e Roy, 1988).”

-Proposta Inicial: A primeira proposta para o fenômeno da RE foi elaborada pouco antes, a partir de 1981, no contexto do estudo sobre eras do gelo [Benzi et al., 1981, 1982, 1983, segundo intro do 1]. [1] Foi observado que as eras glaciais aconteceriam com período da ordem de 10^5 anos, sendo a variação da excentricidade orbital da Terra o único fenômeno cosmológico relevante com período em ordem comparável. Essas variações, contudo, representam uma diferença de no máximo 0,1% no fluxo de entrada de energia solar na superfície da Terra, o que a princípio não seria suficiente para explicar o fenômeno das eras glaciais. [1, intro] A solução proposta modelava o sistema como tendo com dois locos de estabilidade para temperaturas da Terra (essencialmente os estados “em-era-do-gelo” ou “não-em-era-do-gelo”, com uma “barreira” entre eles), uma pequena variação periódica da insolação devido à excentricidade (“sinal”) e variações “aleatórias” anuais de temperatura (“ruído”). A existência das eras do gelo, com sua periodicidade, seria então explicada pelo fenômeno de RE. [1, intro] Sistemas assim são chamados biestáveis. Essa proposta de modelagem acabou por se mostrar limitada [4 e 5, vide “Eras do Gelo” aqui], mas o fenômeno, além das confirmações experimentais já citadas, foi aplicado com sucesso numa grande diversidade de áreas, inclusive no estudo das eras glaciais [vide “Algumas Outras Aplicações”, aqui].

--Outros “Tipos” de RE: Após a proposta do primeiro modelo, classificado como biestável por ter dois locos de estabilidade, mais dois tipos importantes de processos de RE começaram a ser estudados: os detectores de limiar e os excitáveis. Os excitáveis estão relacionados a sistemas com um único estado estável, mas que contam também com um estado excitado de decaimento lento (se comparado à taxa de relaxamento de pequenas perturbações em torno do estado estável). O exemplo [ex] dado na introdução, adicionado de um filtro 1-ou-0, pode ser usado para visualizar RE de limiar. Em particular, de forma bem direta, pode ser usado para exemplificar o efeito da RE na percepção humana de sinais visuais com certas características, como veremos em detalhes a seguir. Sistemas excitáveis e de detecção de limiar acabaram por encontrar aplicação em outros campos, como na neurofisiologia de lagostins. [1]

RE em Detectores de Limiar:

Primeiras noções

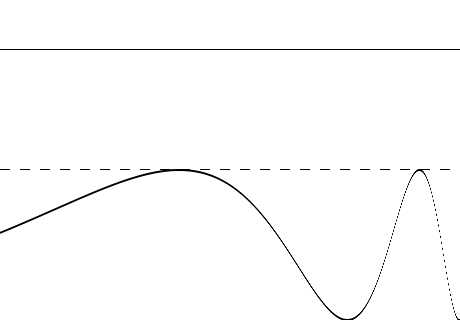
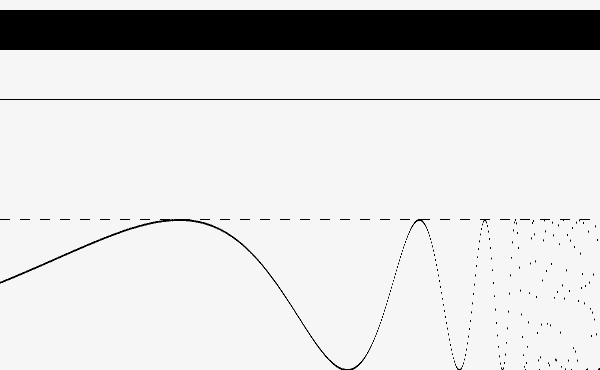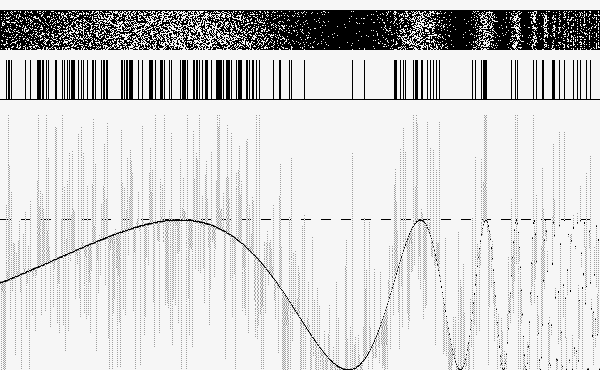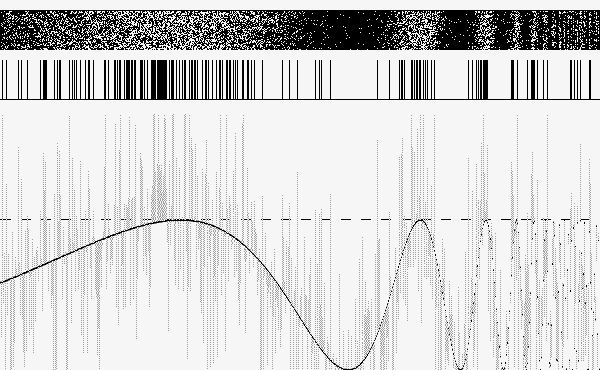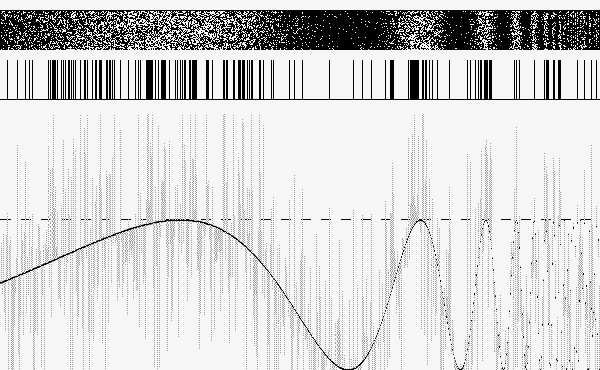
Tomemos inicialmente um sinal com uma intensidade S dada em função de uma posição x, ou seja, S = f(x), sujeito, para todo x, a um limiar de detecção Delta. A saída do nosso sistema será, para cada x, 1 ou 0 (representados por “branco” ou “preto”) , correspondendo apenas à informação de se o sinal cruzou ou não o limiar - a diferença exata não importa. Podemos imaginar três casos: F(x) < Delta para todo x, onde o sinal “some”; F(x) > Delta para todo x, onde “vemos” que o sinal existe e ultrapassa o limiar em todos pontos, mas não temos ideia de sua estrutura interna para além disso. F(x) com algumas regiões acima de Delta e outras abaixo, onde temos um pouco de informação sobre parte dessa estrutura, mas de forma em geral coarsa. A RE pode ajudar a reconstruir a informação do sinal nos três casos, mas nos exemplos a seguir nos focaremos inicialmente no primeiro, representado na figura 1:

Gráfico 1: Sinal abaixo do limiar de detecção.

O sinal - curva na parte de baixo da imagem - não cruza nunca o limiar - linha tracejada horizontal - e portanto não há nenhuma ativação. A adição de uma constante ao sinal essencialmente nos leva para o caso 3, ainda não satisfatório, representado na figura 2:

Gráfico 2: Sinal elevado homogeneamente.

Note-se que a densidade de barras verticais agora parece guardar alguma relação com a forma do sinal original.

Percepção visual

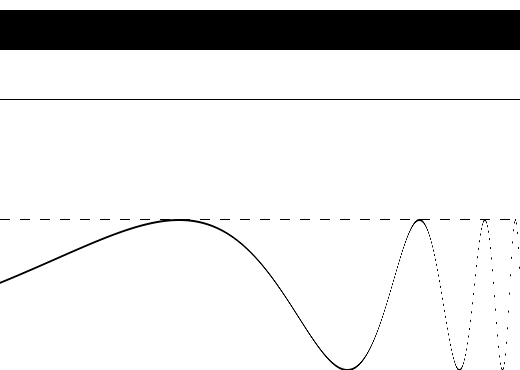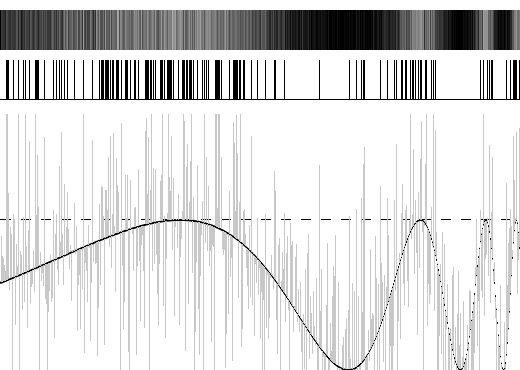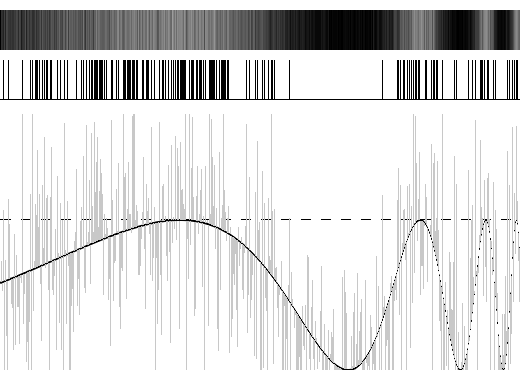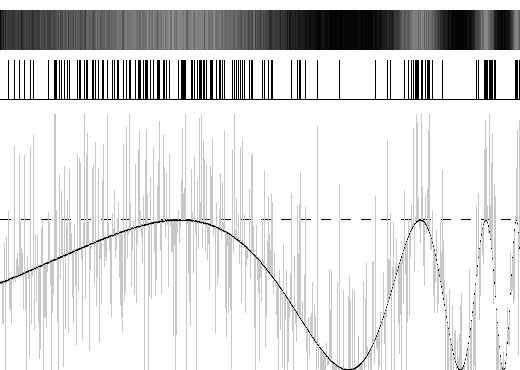
- Reconstruindo o Sinal Orginal: Um próximo passo possível é realizar o ruído diversas vezes, guardando a informação da quantidade de passagens para cada posição, e estudar a proporção entre o número de passagens e o de realizações. A faixa superior da animação 1 mostra justamente isso para S = 75*(1-sen(pi*(1-x))), com 100% = branco e 0% = preto:

Animação 1: Várias realizações do ruído, com visualização da proporção de detecções.

O que acontece é que a natureza da distribuição gaussiana faz com que mesmo pontos muito distantes do limiar possam superá-lo, mas com uma probabilidade menor, a cada realização, em relação à de que outros pontos mais próximos o façam. Como o ruído não guarda autocorrelação, o que acontece com cada ponto em cada realização é independente dos outros, mas a relação entre as probabilidades de cruzamento para cada ponto são constantes e definidas, dependendo apenas do desvio padrão do ruído e da intensidade do sinal em cada ponto. Ao tomar a média, contudo, estamos trazendo o resultado de volta a um espaço de (256 = 2^8) tons de cinza, em vez do espaço binário preto e branco. Uma alternativa ao cálculo dessa proporção seria simplesmente guardar os diferentes resultados de cada realização, codificados da mesma forma anterior, nas diferentes linhas da faixa superior. A animação 2 mostra o resultado desse processo:

Animação 2: Várias realizações do ruído, cada uma usada como uma linha acima.

Nota-se que o efeito se mantém: com algumas poucas realizações já é possível, pela percepção visual, estimar detalhes do original. Além da economia de operações, esse sinal reconstruído se mantém binário: representa mais diretamente o que acontece com o sistema e pode, sem compressão, ser codificado em um arquivo de computador usando 1bit por pixel, em vez dos 8 bits por pixel normalmente usados em imagens em tons de cinza (também sem compressão). Imaginando um sinal 2D, pode-se encontrar uma ligação entre o efeito visto e o processo de dithering [8], que em uma imagem visa justamente diminuir sua paleta de cores mantendo o máximo da percepção de sua informação original.

- O Efeito da Ressonância Estocástica na Percepção Visual: Em 1997 foi publicado um artigo de Enrico Simonotto, Massimo Riani, Charles Seife, Mark Roberts, Jennifer Twitty, e Frank Moss [3] discutindo os efeitos da RE na percepção visual. Em busca de um critério quantitativo objetivo, optaram por usar, em vez de imagens naturais, sinais 1D com regiões de frequência definível. Aos participantes do estudo foram mostradas imagens contendo faixas de “reconstituição” do sinal a partir de linhas construídas por diferentes realizações do ruído, como se vê na faixa da animação 2. A diferença principal é que em vez de atualizar uma linha por vez, toda a faixa era atualizada 60 vezes por segundo. Cada imagem continha sete faixas, cada faixa sendo elaborada a partir de um sinal da forma A*sin(1/x) + 128 , com Delta = 150 e diferentes amplitudes A, como 28 ou 128. Além disso, todas faixas eram submetidas a um ruído de mesma intensidade (mesmo desvio padrão), que variava a cada aplicação do teste. O teste consistia em pedir para o participante contar até que faixa (ou seja, para qual amplitude mínima) era capaz de discernir uma dada estrutura, efetivamente permitindo a construção de um gráfico de amplitude mínima vs intensidade do ruído. A animação 3 foi baseada nisso, para efeito ilustrativo. A faixa mais acima seria uma representação ideal (em tons de cinza, 8bits) do sinal com amplitude 256. As demais têm amplitudes que vão diminuindo de baixo para cima. O limiar de corte e a intensidade do ruído são os mesmos para todas faixas, sendo que o desvio padrão do ruído vai aumentando com o tempo:

Animação 3: Várias realizações de ruídos com diferentes desvios padrão, sobre uma sequência de faixas de um sinal com diferença apenas de amplitude e sob o mesmo limiar. A faixa do topo representa um sinal “idealmente representado” em tons de cinza e com amplitude 256.

O estudo encontrou de fato, para cada participante, uma curva apontando um nível ideal de ruído: menos e algumas estruturas não aparecem direito, mais e o ruído começa a dominar a imagem. Esse efeito, que é perceptível na animação 3, ajuda a justificar o termo Ressonância Estocástica. Curiosamente, a diferença entre as curvas encontradas para cada participante pôde ser justificada por uma simples constante multiplicativa. Essa constante, variou muito pouco mediante repetições do teste pelo mesmo participante, mesmo com espaçamento de semanas entre repetições, sugerindo uma possível medida objetiva da capacidade de percepção desse tipo de estímulo visual. Outro ponto levantado pelo estudo, que pode se conferido por uma comparação entre as animações 2 e 3, é que o efeito temporal acentuou a capacidade de percepção em relação a imagens estáticas das realizações do ruído.