Equações de Laplace e Poisson - Eletrostática

Nesta página resolvemos alguns problemas de eletrostática, através da resolução das equações de Laplace e de Poisson com condições de contorno. Apresentamos a solução analítica (se houver) e a solução numérica utilizando dois métodos. Os métodos numéricos aqui utlizados são denomindos de métodos de relaxação: método de Jacobi e método de Gauss-Seiedel.

Eletrostática

As equações de Laplace e Poisson surgem muito naturalmente no contexto da eletrostática. Para obtermos tais equações, comecemos com a Lei de Gauss para a eletrostática

$\nabla \cdot E={\frac {\rho }{\epsilon _{0}}}$

onde $E$ é o campo elétrico, $\rho$ é a densidade de carga elétrica e $\epsilon _{0}$ é a permissividade elétrica do vácuo.

Podemos relacionar o campo elétrico com o potencial elétrico pela seguinte relação

$E=-\nabla V$

Substituindo na expressão anterior, encontramos a equação de Poisson

$\nabla ^{2}V=-{\frac {\rho }{\epsilon _{0}}}$

Se tomarmos o caso em que a densidade de cargas é nula, ou seja, não há cargas no meio, então obtemos a equação de Laplace

$\nabla ^{2}V=0$

Em problemas de eletrostática, o objetivo geralmente reside em encontrar o campo elétrico. Em muitos casos é mais fácil encontrarmos primeiro o potencial através das equações de Laplace ou Poisson e então, através de um gradiente, obtermos o campo elétrico. Isso ocorre devido à necessidade de termos condições de contorno para que as equações de Laplace e Poisson sejam devidamente resolvidas.

Nas próximas seções, resolveremos alguns problemas em que serão dados as condições de contorno para o potencial elétrico e através dessa informação será possível obter finalemente o campo elétrico.

Métodos númericos

Neste trabalho, resolvemos os problemas de eletrostática através dos chamados métodos de relaxação. Utilizamos dois algoritmos diferentes: o algoritmo de Jacobi e o algoritmo de Gauss-Siedel. Antes de apresentarmos estes algoritmos, vamos fazer algumas considerações gerais sobre o método de relaxação.

Vamos iniciar com a equação da difusão, uma equação que envolve derivadas parciais em relação oa tempo e espaço

${\frac {\partial {\bar {V}}(x,y,z,t)}{\partial t}}=D\left({\frac {\partial ^{2}{\bar {V}}}{\partial x^{2}}}+{\frac {\partial ^{2}{\bar {V}}}{\partial y^{2}}}+{\frac {\partial ^{2}{\bar {V}}}{\partial z^{2}}}\right)$.

Como as equações de Laplace e Poisson são equações independentes do tempo, as soluções estacionárias da equação da difusão serão também solução das equações de Laplace e Poisson. O processo de difusão tem um limite de equilíbrio, isto é, em algum momento o estado não vai depender do tempo. Conforme veremos a seguir, o algoritmo de Jacobi faz com que o sistema evolua de acordo com a equação de difusão. Mas como o sistema deve ser estacionário (não depender mais do tempo), a derivada de ${\bar {V}}$ com relação ao tempo deve se anular e recaímos na equação de Laplace.

A seguir apresentamos os dois algoritmos de relaxação.

Algoritmo de Jacobi

Tanto na equação de Laplace quanto na equação de Poisson, há derivadas segundas de uma função (no nosso caso aqui será sempre o potencial elétrico). Com isso, para discretizar as equações de Laplace e Poisson, precisamos discretizar as derivadas. Podemos utilizar tanto derivadas à direita, quanto à esquerda, quanto centradas

${\frac {\partial V}{\partial x}}\approx {\frac {V(i+1,j,k)-V(i,j,k)}{\Delta x}}$

${\frac {\partial V}{\partial x}}\approx {\frac {V(i,j,k)-V(i-1,j,k)}{\Delta x}}$

${\frac {\partial V}{\partial x}}\approx {\frac {V(i+1,j,k)-V(i-1,j,k)}{2\Delta x}}$

Como estamos interessados em derivadas segundas, podemos escrever estas como uma combinação da derivada centrada, de forma que

${\frac {\partial ^{2}V}{\partial x^{2}}}\approx {\frac {1}{\Delta x}}\left[{\frac {\partial V}{\partial x}}\left(i+{\frac {1}{2}}\right)-{\frac {\partial V}{\partial x}}\left(i-{\frac {1}{2}}\right)\right]$

onde ${\frac {\partial V}{\partial x}}\left(i+{\frac {1}{2}}\right)$ pode ser entendida como uma derivada centrada em um ponto imaginário $\left(i+{\frac {1}{2}}\right)$ que é idêntica a uma derivada à direita. O mesmo raciocínio pode ser aplicado para ${\frac {\partial V}{\partial x}}\left(i-{\frac {1}{2}}\right)$. Dessa forma, a derivada segunda pode ser escrita como

${\frac {\partial ^{2}V}{\partial x^{2}}}\approx {\frac {1}{\Delta x}}\left[{\frac {V(i+1,j,k)-V(i,j,k)}{\Delta x}}-{\frac {V(i,j,k)-V(i-1,j,k)}{\Delta x}}\right]$

E rearanjando os termos, encontramos

${\frac {\partial ^{2}V}{\partial x^{2}}}\approx {\frac {V(i+1,j,k)+V(i-1,j,k)-2V(i,j,k)}{(\Delta x)^{2}}}$

As derivadas parciais (primeiras e segungas) para $y$ e $z$ são completamente análogas. Se nós considerarmos que os passos ao longo de $x$, $y$ e $z$ são iguais, então $\Delta x=\Delta y=\Delta z$, e podemos escrever a equação de Laplace como

$V(i,j,k)={\frac {1}{6}}\left[V(i+1,j,k)+V(i-1,j,k)+V(i,j+1,k)+V(i,j-1,k)+V(i,j,k+1)+V(i,j,k-1)\right]$.

Isso significa que o valor do potencial em qualquer ponto é a média dos valores de $V$ nas vizinhanças do ponto. Para um dado $V_{0}$ inicial, nós calculamos um $V_{1}$ através desta última expressão. Com $V_{1}$, é possível calcularmos $V_{2}$ e assim por diante, até que a solução convirja para um dado valor. É necessário estabelecer uma tolerância para saber até onde precisamos aplicar o algoritmo. Com o intuito de enfatizar essa evolução temporal de $V$, vamos reescrever a última expressão como

$V_{i,j,k}^{n+1}={\frac {1}{6}}\left[V_{i+1,j,k}^{n}+V_{i-1,j,k}^{n}+V_{i,j+1,k}^{n}+V_{i,j-1,k}^{n}+V_{i,j,k+1}^{n}+V_{i,j,k-1}^{n}\right]$.

onde os índices $i,j,k$ se referem às coordenadas espaciais $x,y,z$ e $n$ se refere ao instante de tempo.

De forma completamente análoga, podemos escrever a equação de Poisson discretizada da seguinte forma

$V(i,j,k)={\frac {1}{6}}\left[V(i+1,j,k)+V(i-1,j,k)+V(i,j+1,k)+V(i,j-1,k)+V(i,j,k+1)+V(i,j,k-1)\right]+{\frac {\rho (i,j,k)\Delta x^{2}}{6}}$

onde assumimos novamente que $\Delta x=\Delta y=\Delta z$.

Novamente reescrevendo a expressão para a equação de Poisson, obtemos

$V_{i,j,k}^{n+1}={\frac {1}{6}}\left[V_{i+1,j,k}^{n}+V_{i-1,j,k}^{n}+V_{i,j+1,k}^{n}+V_{i,j-1,k}^{n}+V_{i,j,k+1}^{n}+V_{i,j,k-1}^{n}\right]+{\frac {\rho _{i,j,k}^{n}(\Delta x)^{2}}{6}}$.

Como este algoritmo é um algoritmo iterativo, precisamos escolher uma tolerância na qual o algoritmo pare de calcular a solução, pois ela já é boa o suficiente para o nosso objetivo. Devemos ter em mente, que uma tolerância cada vez menor, implica em uma solução cada vez mais próxima da solução correta, entretanto, isto significa um tempo e gasto computacional maior. É necessário analisar as vantagens e/ou necessidades de uma solução mais, ou menos, exata.

Algoritmo de Gauss-Siedel

O algoritmo de Gauss-Siedel é uma melhoria no algoritmo de Jacobi. Enquanto o algoritmo de Jacobi utiliza somente os valores antigos para construir o novo, o algoritmo de Gauss-Siedel utiliza os novos valores, assim que eles ficam disponíveis. Consideremos o caso bidimensional, vamos supor que você vai percorrer as linhas (indo do menor $i$ para o maior $i$) da sua cela, mantendo a coluna ($j$) constante. Nesse caso, os valores $V_{i-1,j}^{n+1}$ e $V_{i,j-1}^{n+1}$ já serão conhecidos, de modo que podemos escrever o algoritmo de Gauss-Siedel como

$V_{i,j}^{n+1}={\frac {1}{4}}\left[V_{i+1,j}^{n}+V_{i-1,j}^{n+1}+V_{i,j+1}^{n}+V_{i,j-1}^{n+1}\right]$.

A melhoria na performance do algoritmo de Gauss-Siedel em comparação com o de Jacobi é apenas um fator 2.

Exemplos

Caixa com bordas carregadas

A caixa deste problema é bidimensional é ilustrada na Figura 1. As laterais em x = 1 e x = -1 estão fixadas a um potencial elétrico de V = 1 e V = -1, respectivamente,pois são superfícies condutoras. As bordas superiores, em y = 1 e y = -1 são superfícies isolantes, logo o potencial varia de forma linear. No interior da caixa, o potencial é inicialmente zero pois são há cargas. Com a utilizando a equação de Laplace e as condições de contorno dadas, podemos resolver este problema analiticamente e numericamente.

Como não há condutores no interior da caixa, esperamos que quando o tempo evoluir, o potencial no interior da caixa seja igual ao potencial nas superfícies isolantes y = 1 e y = -1. Na direção $y$ o potencial é constante, enquanto que na direção $x$, ele varia de V = -1 à V = 1.

Como o campo elétrico é perpendicular às equipotenciais, o campo elétrico será inteiramente na direção $x$ e orientado na direção em que o potencial decresce, ou seja, para a esquerda.

Resultado numérico

Numericamente, construímos uma matriz quadrada de L = 61 linhas e colunas, com as devidas condições de contorno nas bordas. Utilizamos um lado de 61 para que o problema ficasse simétrico em relação à origem, logo temos 30 colunas à esquerda e 30 colunas à direita da coluna central. Esta abordagem simétrica foi utilizada em todos os exemplos resolvidos aqui.

Com a condição de contorno inicial, aplicamos o algoritmo de Jacobi e escolhemos uma tolerância de $10^{-5}\times L^{2}$. Toda a iteração é feita somente dentro da caixa, sem modificarmos as bordas. Um chute inicial para a inicialização da matriz dentro das bordas é que todas os sítios estejam no potencial nulo.

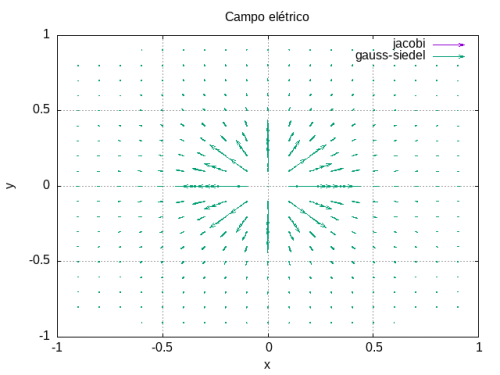
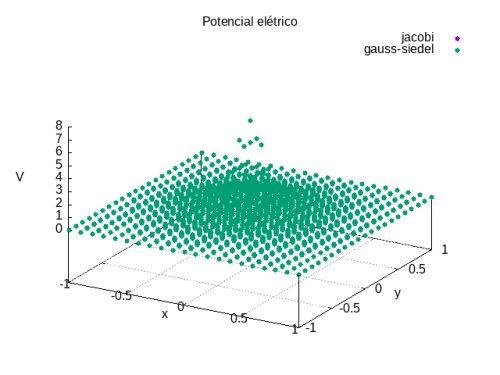
Na Figura 2, apresentamos o potencial elétrico em um gráfico 3D. Na Figura 3, apresentamos as linhas equipotenciais. E na Figura 4, apresentamos o campo elétrico obtido através do potencial.

Com o algoritmo de Gauss-Siedel, obtivemos uma solução muito próxima à obtida com o algoritmo anterior. Nas próximas figuras, apresentamos o potencial, as linhas equipotenciais e o campo elétrico.

Na figura $$, apresentamos um gráfico do erro dos algoritmos com o resultado analítico.

Prisma com condutor interno

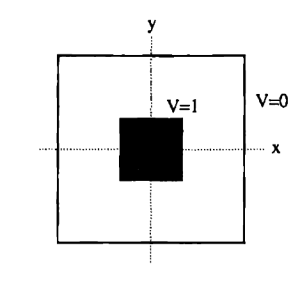
Neste problema assumimos um prisma retangular infinito na direção $z$. Este prisma é metálico e está sujeito a um potencial nulo fixo. O prisma condutor interno está sujeito a um potencial V = 1. Nosso objetivo é descobrir o potencial e o campo elétrico entre os dois prismas. Abaixo apresentamos um corte esquemático do prisma.

Desenho esquemático da geometria do problema. Giordano e Nakanishi.

É importante mencionar que este problema não possui solução analítica.Com isso, você pode se perguntar, como podemos testar o método, se não conhecemos a solução analítica do problema? A resposta para esta pergunta reside no fato de que nós podemos inferir qual deve ser o resultado esperado baseado na simetria do problema. Da mesma forma que no exemplo anterior, onde o potencial decresceu de V = 1 até V = -1, aqui nós esperamos que ele decresça de V = 1 no prisma central até V = 0 nas bordas. Qualquer resultado diferente disso, já nos mostra problemas com o método. Mas e como saberemos que o resultado mostrado, mesmo respeitando esta simetria, é o correto? Bom, aplicando o método a um número suficientes de problemas com resposta analítica conhecida nos dá confiança no método, de forma que podemos "confiar", com cautela, nos seus resultados fornecidos. Cm isso, vamos aos resultados numéricos.

Resultado numérico

Considerando o prisma exterior tendo um lado 2 e o condutor interno tendo um lado 0.6. Foi considerado um espaçamento espacial de 0.01, logo utilizamos uma matriz quadrada de tamanho L = 201.

Novamente, com a condição de contorno inicial, aplicamos o algoritmo de Jacobi e escolhemos uma tolerância de $10^{-5}\times L^{2}$. Aplicamos o algoritmo de Gauss-Siedel utilizando a mesma condição de contorno inicial.

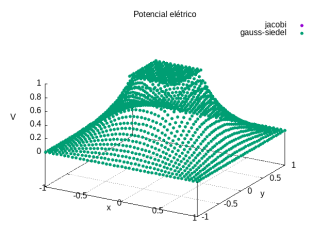
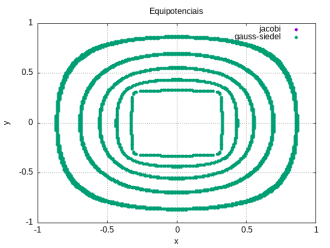
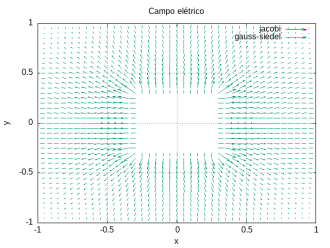
Abaixo apresentamos o potencial elétrico em um gráfico 3D, as linhas equipotenciais eo campo elétrico obtido através do potencial.

Potencial elétrico para o interior do prisma externo.

Linhas equipotenciais para o interior do prisma externo.

Campo elétrico para o interior do prisma externo.

Capacitores paralelos

Neste problema, vamos encontrar o potencial e o campo elétrico para duas placas paralelas submetidas a um potencial de V = -1 e V = 1. Na Figura $$ apresentamos um desenho esquemático do problema. Novamente, o problema é em duas dimensões por possuir simetria em relação ao eixo z. A caixa na qual as placas estão inseridas estão fixadas a um potencial nulo.

Entretanto, diferente do problema anterior, agora nós temos uma dificuldade extra, caso quiséssemos atacar este problema de forma analítica. Temos efeitos de distorção devido às bordas finitas das placas, logo o campo elétrico não será, de forma alguma, simples nas vizinhanças superiores e inferiores das placas. Uma solução numérica é a única alternativa.

Resultado numérico

Vamos novamente escrever uma matriz de lado L = 201 e assumir que a caixa tem lado 1. Vamos inicializar todos os sítios em 0, menos nas placas, que estão a uma distância de 0.3 da origem. Escolhemos novamente a tolerância de $10^{-5}\times L^{2}$.

Nas figuras posteriores apresentamos o potencial elétrico em um gráfico tridimensional, as linhas equipotenciais e o campo elétrico.

Aplicamos o algoritmo de Gauss-Siedel utilizando a mesma condição de contorno inicial. Nas próximas figuras, mostramos o potencial em um gráfico em 3D, as linhas equipotenciais e o campo elétrico.

Caixa com carga pontual

Este é o primeiro problema em que cargas elétricas estão envolvidas, ou seja, temos que resolver numericamente a equação de Poisson ao invés da equação de Laplace. Vamos considerar uma caixa tridimensional (um cubo) de lado 2 e colocar a carga elétrica no centro desse cubo, conforme a Figura $$. Vamos fixar o potencial da caixa em V = 0 e calcular o potencial elétrico e o campo elétrico dessa carga. Devemos nos lembrar que a solução analítica para este problema, ou seja, o potencial elétrico para uma carga pontual é

$V(r)={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{r}}$

onde $q$ é a carga da partícula e $r$ é a distância entre o ponto em que estamos calculando o potencial e a carga.

Resultado numérico

Para resolver com o método de Jacobi, inicializamos uma matriz com lado L = 21, ou seja, o tamanho dos sítios foi de 0.1. Utilizamos unidades em que $q/\epsilon _{0}=1$ e onde a constante dielétrica no vácuo é a unidade. Inicializamos uma matriz $\rho$ de mesmo tamanho com todos os sítios nulos exceto o sítio central e seus primeiros vizinhos (esquerda, direita, cima, baixo, frente e atrás). A seguir mostramos os gráficos do potencial e do campo elétrico para este problema.

Campo elétrico para a carga pontual.

Campo elétrico para a carga pontual.

Códigos

Todos os códigos foram escritos em FORTRAN e podem ser acessados aqui.

Exemplo 1 - Caixa com bordas carregadas

Exemplo 2 - Prisma com condutor interno

Exemplo 3 - Capacitores paralelos

Exemplo 4 - Caixa com carga pontual

Referências

Giordano, N. J. Nakanishi, H. Computational Physics. Pearson Prentice Hall, 2ª ed. 2006.

Griffiths, D. Eletrodinâmica. Pearson 3ª ed. São Paulo.

Scherer, C. Métodos Computacionais da Física. Livraria da Física, 2ª ed. 2010.