Grupo3 - Ondas2

Introdução

Equações diferenciais parciais (EDP's) hiperbólicas geralmente podem ser formuladas a partir de teoremas de conservação. Um exemplo é a equação do tipo:

${\frac {\partial {\vec {U}}}{\partial t}}+\nabla \cdot {\vec {F}}(U)={\vec {S}}(U)$,

onde ${\vec {U}}$ é o vetor de densidades da quantidade conservada, i.e., ${\vec {U}}=(U_{1},...,U_{n})$, ${\vec {F}}$ é o fluxo de densidade e ${\vec {S}}$ é um termo genérico representando fontes ou sumidouros.

Uma classe especial de equações hiperbólicas são as chamadas equações de adveção, na qual a derivada temporal da quantidade conservada ${\vec {U}}({\vec {x}},t)$ é proporcional à sua derivada espacial. Nesses casos, ${\vec {F}}(U)$ é diagonal e dada por:

${\vec {F}}(U)=v{\vec {I}}\cdot {\vec {U}}$,

onde ${\vec {I}}$ é a matriz identidade.

Considerando apenas uma dimensão e com ${\vec {U}}\equiv u$, temos a equação de adveção:

${\frac {\partial u}{\partial t}}+v{\frac {\partial u}{\partial x}}=0$,

onde $v$ é a velocidade de propagação do pulso gerado. A equação admite uma solução analítica da forma $u=f(x-vt)$, representando uma onda se movendo na direção $x$.

A equação da onda em uma dimensão é uma EDP hiperbólica de segunda ordem dada por

${\frac {\partial ^{2}u}{\partial t^{2}}}=v^{2}{\frac {\partial ^{2}u}{\partial x^{2}}}.$

E admite duas soluções, representadas por pulsos, $f(x+vt)$ e $f(x-vt)$.

Assumindo que $v\neq v(x)$ na equação da onda, nos restringimos a problemas lineares. Além disso, se escrevermos

$k=v{\frac {\partial u}{\partial x}}$, $s={\frac {\partial u}{\partial t}},$

então a equação da onda pode ser escrita como um sistema de três equações diferenciais de primeira ordem:

${\begin{cases}{\frac {\partial k}{\partial t}}=v{\frac {\partial s}{\partial x}}\\{\frac {\partial s}{\partial t}}=v{\frac {\partial k}{\partial x}}\\{\frac {\partial u}{\partial t}}=s\end{cases}}$

Em notação vetorial, o sistema acima pode ser reescrito na forma conservativa como: ${\frac {\partial U}{\partial t}}+{\frac {\partial F(U)}{\partial x}}=0$,

onde $U={\begin{pmatrix}k\\s\end{pmatrix}},\quad {\textrm {e}}\quad F(U)={\begin{pmatrix}0&-v\\-v&0\end{pmatrix}}$

O Problema Físico

O Modelo de Corda Ideal

Para uma primeira abordagem da equação da onda, podemos primeiro dividir o comprimento $L$ da corda em $K$ intervalos de comprimentos iguais, dessa forma $\Delta x={\frac {L}{K}}$. Cada intervalo é discretizado, representado por $x_{i}$, $i=0,1,...,K$. Também podemos dividir o tempo em intervalos iguais $\Delta t$ e denotá-los como $t_{n}$, $n=0,1...$.

Tendo feita a discretização das variáveis, podemos aproximar a equação da onda por diferenciação finita, utilizando derivadas centradas da seguinte forma:

${\frac {\partial ^{2}u}{\partial t^{2}}}={\frac {U_{i}^{n+1}-2U_{i}^{n}+U_{i}^{n-1}}{\Delta t^{2}}}$

${\frac {\partial ^{2}u}{\partial x^{2}}}={\frac {U_{i+1}^{n}-2U_{i}^{n}+U_{i-1}^{n}}{\Delta x^{2}}}$

onde $U_{i}^{n}$ representa o valor discretizado de $u(x_{i},t_{n})$.

Assim, chegamos em uma equação discretizada:

${\frac {U_{i}^{n+1}-2U_{i}^{n}+U_{i}^{n-1}}{(\Delta t)^{2}}}=v^{2}{\frac {U_{i+1}^{n}-2U_{i}^{n}+U_{i-1}^{n}}{(\Delta x)^{2}}}$.

Sabendo que essa discretização da equação da onda pode ser verificada como sendo o método Leapfrog (ver seção do método de Leapfrog), podemos resolver a equação para $U_{i}^{n+1}$ para sabermos o deslocamento de uma partição da corda no momento de tempo seguinte, assim obtendo

$U_{i}^{n+1}=2(1-r^{2})U_{i}^{n}+r^{2}[U_{i+1}^{n}+U_{i-1}^{n}]-U_{i}^{n-1}$,

onde $r=v{\frac {\Delta t}{\Delta x}}.$

Um Quadro Mais Realístico - O Modelo de Corda Rígida

Para nos aproximarmos de um modelo mais real, podemos adicionar um termo à equação original da onda que corresponde ao efeito de fricção em uma corda. De acordo com [1], a equação da onda mais geral com efeito de fricção pode ser escrita como

${\frac {\partial ^{2}y}{\partial t^{2}}}=v^{2}\left({\frac {\partial ^{2}y}{\partial x^{2}}}-\epsilon L^{2}{\frac {\partial ^{4}y}{\partial x^{4}}}\right),$

onde $v$ é a velocidade transversal de propagação do pulso na corda, dada pela relação $v={\sqrt[{}]{\frac {T}{\rho }}}$ (sendo $T$ a tensão na corda e $\rho$ a densidade linear da mesma), $\epsilon$ é um parâmetro adimensional de fricção que representa a rigidez da corda e $L$ o comprimento da corda.

O parâmetro $\epsilon$ é dado por

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon = \kappa² \frac{E S}{T L^2}} ,

onde $\kappa$ é o raio da corda, $E$ é o Módulo de Young e $S$ a área da secção da corda.

Ao discretizarmos a equação da onda em uma corda com fricção e a resolvendo para $u_{i}^{n+1}$ obtemos:

$u_{i}^{n+1}=[2-2r^{2}-6\epsilon r^{2}K^{2}]u_{i}^{n}-u_{i}^{n-1}+r^{2}[1+4\epsilon K^{2}][u_{i+1}^{n}+u_{i-1}^{n}]-\epsilon r^{2}K^{2}[u_{i+2}^{n}+u_{i-2}^{n}].$

O fato de essa discretização depender do deslocamento da corda em posições $i-2$ e $i+2$ implica em precisarmos simular "pontos fantasmas" quando integramos os extremos das cordas. Para fazermos isso, podemos ou utilizar a aproximação $u_{-1}^{n}=-u_{+1}^{n}$ ou podemos considerar esses "pontos fantasmas" como pontos presos e, portanto, sempre iguais a zero.

Os Métodos Utilizados

Foi realizada uma abordagem ao problema da corda real a partir de três métodos diferentes de integração numérica. Os três são métodos para fins de resolução de equações diferenciais parciais da forma apresentada anteriormente.

O método mais básico é chamado de FTCS (Forward-Time-Centered-Space) e consiste em duas expansões de Taylor ao redor do ponto $x_{j}$:

$u(x_{i}+\Delta x,t^{n})=u(x_{i},t^{n})+{\frac {\partial u}{\partial x}}(x_{i},t^{n})\Delta x+{\frac {1}{2}}{\frac {\partial ^{2}u}{\partial x^{2}}}(x_{i},t^{n})\Delta x^{2}+{\mathcal {O}}(\Delta x^{3}),$

$u(x_{i}-\Delta x,t^{n})=u(x_{i},t^{n})-{\frac {\partial u}{\partial x}}(x_{i},t^{n})\Delta x+{\frac {1}{2}}{\frac {\partial ^{2}u}{\partial x^{2}}}(x_{i},t^{n})\Delta x^{2}+{\mathcal {O}}(\Delta x^{3}).$

Subtraindo as duas expressões, encontramos a expressão

$\left.{\frac {\partial u}{\partial x}}\right|_{i}^{n}={\frac {u_{i+1}^{n}-u_{i-1}^{n}}{2\Delta x}}+{\mathcal {O}}(\Delta x^{2})$,

A qual podemos substituir na equação da onda, juntamente com a discretização da derivada parcial temporal. Temos então que, para um sistema linear de equações hiperbólicas:

${\textbf {U}}_{i}^{n+1}={\textbf {U}}_{i}^{n}-{\frac {\Delta t}{2\Delta x}}[{\textbf {F}}_{i+1}^{n}-{\textbf {F}}_{i-1}^{n}]+{\mathcal {O}}(\Delta t^{2},\Delta x^{2}\Delta t)$

Visto que essa última notação é mais genérica, ela será utilizada para a explicação dos métodos posteriores.

O Método de Lax-Friedrichs

O método de Lax-Friedrichs consiste em substituir o termo ${\textbf {U}}_{i}^{n}$ com sua respectiva média espacial, i.e., $u_{i}^{n}=(u_{i+1}^{n}+u_{i-1}^{n})/2$. Logo, temos a seguinte equação de recorrência:

${\textbf {U}}_{i}^{n+1}={\frac {1}{2}}({\textbf {U}}_{i+1}^{n}+{\textbf {U}}_{i-1}^{n})-{\frac {\Delta t}{2\Delta x}}[{\textbf {F}}_{i+1}^{n}-{\textbf {F}}_{i-1}^{n}]+{\mathcal {O}}(\Delta x^{2})$

O Método de Leapfrog

Tanto o método FTCS quanto o método de Lax-Friedrichs são métodos de primeira ordem para a derivada temporal. Nessas circunstâncias, $v\Delta t$ deve ser significantemente menor do que $\Delta x$, muito abaixo do limite imposto pela condição de Courant (ver seção estabilidade dos métodos).

Uma nova expressão para a derivada temporal, com precisão de segunda ordem é dada por

$\left.{\frac {\partial u}{\partial t}}\right|_{i}^{n}={\frac {u_{i}^{n+1}-u_{i}^{n-1}}{2\Delta t}}+{\mathcal {O}}(\Delta t^{2}).$

Substituindo a nova expressão acima no método de FTCS discutido anteriormente, encontramos o método de Leapfrog:

${\textbf {U}}_{i}^{n+1}={\textbf {U}}_{i}^{n-1}-{\frac {\Delta t}{\Delta x}}[{\textbf {F}}_{i+1}^{n}-{\textbf {F}}_{i-1}^{n}]+{\mathcal {O}}(\Delta x^{2}).$

Como o método de Leapfrog foi o mais aplicado na resolução do problema em questão, é interessante um aprofundamento maior do método. Podemos adaptar o método de Leapfrog para o sistema de equações definido para a equação da onda ao fazermos

$k_{i+{\frac {1}{2}}}^{n}\equiv v\left.{\frac {\partial u}{\partial x}}\right|_{i+{\frac {1}{2}}}^{n}=v{\frac {u_{i+1}^{n}-u_{i}^{n}}{\Delta x}}+{\mathcal {O}}(\Delta x)\qquad (1)$

$s_{i}^{n+{\frac {1}{2}}}\equiv \left.{\frac {\partial u}{\partial t}}\right|_{i}^{n+{\frac {1}{2}}}={\frac {u_{i}^{n+1}-u_{i}^{n}}{\Delta t}}+{\mathcal {O}}(\Delta t)\qquad (2)$

Com a representação Leapfrog das equações do sistema de três equações, temos:

$k_{i+{\frac {1}{2}}}^{n+1}=k_{i+{\frac {1}{2}}}^{n}+r(s_{i+1}^{n+{\frac {1}{2}}}-s_{i}^{n+{\frac {1}{2}}})+{\mathcal {O}}(\Delta x^{2})\qquad (3)$

$s_{i}^{n+{\frac {1}{2}}}=s_{i}^{n-{\frac {1}{2}}}+r(k_{i+{\frac {1}{2}}}^{n}-k_{i-{\frac {1}{2}}}^{n})+{\mathcal {O}}(\Delta x^{2})\qquad (4)$

Com essas duas equações, podemos fazer uma integração utilizando o método de Euler para obter $u_{j}^{n+1}$, ou seja, o deslocamento de um determinado ponto no próximo instante de tempo:

$u_{i}^{n+1}=u_{i}^{n}+{\frac {\Delta t}{2}}s_{i}^{n+{\frac {1}{2}}}+{\mathcal {O}}(\Delta x^{2}).$ Contudo, podemos fazer uma simples substituição das equações $(1)$ e $(2)$ nas equações $(3)$ e $(4)$ e, assim, obtemos que a representação de Leapfrog da equação da onda é dada pela discretização de segunda ordem da própria equação da onda, com ${\mathcal {O}}(\Delta t^{2},\Delta x^{2})$. Isso nos dá uma solução de "um passo", onde só precisamos efetuar o cálculo da equação discretizada.

O Método de Lax-Wendroff

O método de Lax-Wendroff é a extensão do método de Lax-Friedrichs de segunda ordem. Calculamos o vetor $U$ a partir de um passo médio de Lax-Friedrichs:

${\textbf {U}}_{i+{\frac {1}{2}}}^{n+{\frac {1}{2}}}={\frac {1}{2}}[{\textbf {U}}_{i+1}^{n}+{\textbf {U}}_{i}^{n}]-{\frac {\Delta t}{2\Delta x}}[{\textbf {F}}_{i+1}^{n}-{\textbf {F}}_{i}^{n}]+{\mathcal {O}}(\Delta x^{2})$,

${\textbf {U}}_{i-{\frac {1}{2}}}^{n+{\frac {1}{2}}}={\frac {1}{2}}[{\textbf {U}}_{i}^{n}+{\textbf {U}}_{i-1}^{n}]-{\frac {\Delta t}{2\Delta x}}[{\textbf {F}}_{i}^{n}-{\textbf {F}}_{i-1}^{n}]+{\mathcal {O}}(\Delta x^{2})$,

E encontramos os fluxos ${\textbf {F}}_{i\pm {\frac {1}{2}}}^{n+{\frac {1}{2}}}$ a partir dos valores de ${\textbf {U}}_{i\pm {\frac {1}{2}}}^{n+{\frac {1}{2}}}.$

Logo, com um meio passo de Leapfrog, temos a expressão final do método:

${\textbf {U}}_{i}^{n+1}={\textbf {U}}_{i}^{n}-{\frac {\Delta t}{\Delta x}}[{\textbf {F}}_{i+{\frac {1}{2}}}^{n+{\frac {1}{2}}}-{\textbf {F}}_{i-{\frac {1}{2}}}^{n+{\frac {1}{2}}}]+{\mathcal {O}}(\Delta x^{2})$

Análise e Discussão dos Resultados

Escolhemos para simular quatro diferentes cordas: as cordas C2, C4 e C7 de um piano cujos dados foram obtidos no artigo sobre cordas do Chaigne \cite{artigo} e uma corda com dados pré-estabelecidos encontrados no livro de física computacional do Giordano \cite{giordano}. Os dados das cordas C2, C4 e C7 estão na tabela abaixo.

	C2	C4	C7
Comprimento ($m$)	1.90	0.62	0.09
Massa($g$)	35	3.93	0.467
Tensão ($N$)	750	670	750
Divisões	100	50	16
Amostragem de sinal	16	32	96
Parâmetro de fricção	$7.5\times 10^{-6}$	$3.82\times 10^{-5}$	$8.67\times 10^{-4}$

Desses dados, temos que a densidade linear de massa das cordas é dada por $\rho ={\frac {M}{l}},$ onde $M$ é a massa e $l$ o comprimento da corda, $v={\sqrt {\frac {T}{\rho }}},$ onde $T$ é a tensão na corda, $\Delta x={\frac {l}{K}},$ $\Delta t={\frac {1}{f_{e}}},$ e $r=v{\frac {\Delta t}{\Delta x}}.$ Para a corda com dados pré-estabelecidos, utilizamos uma corda com 2 metros de comprimento, com velocidade de propagação da onda sendo 300$m/s$, $\Delta x$ de 0.01$m$, $\Delta t={\frac {\Delta x}{4v}}$ e parâmetro de fricção de $7.5\times 10^{-6}$. Supondo a corda inicialmente em repouso, temos que em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = 0<\math> a corda recebe em seu centro o equivalente à batida do martelo do piano. Supomos que esse estímulo possuía o formato aproximado de uma Gaussiana com amplitude de <math>\frac{1}{4}} do comprimento da corda. Então, com o estado inicial sendo um pulso com o formato de um pacote gaussianico e os dados da tabela, simulamos a propagação de ondas em cada uma das cordas.

Utilizando o método de Leapfrog, foi realizada uma primeira simulação para uma onda ideal em uma corda:

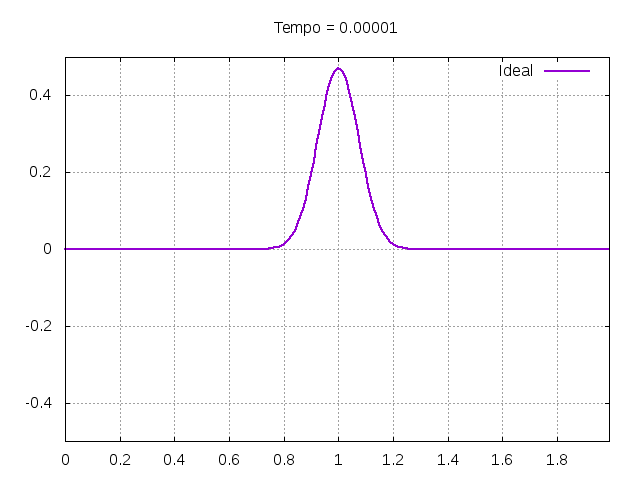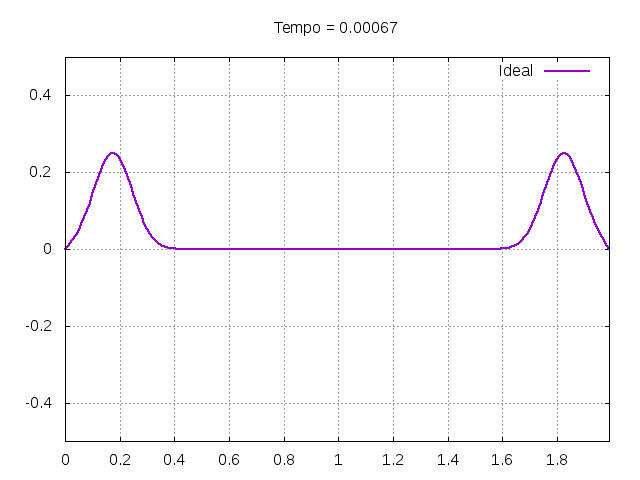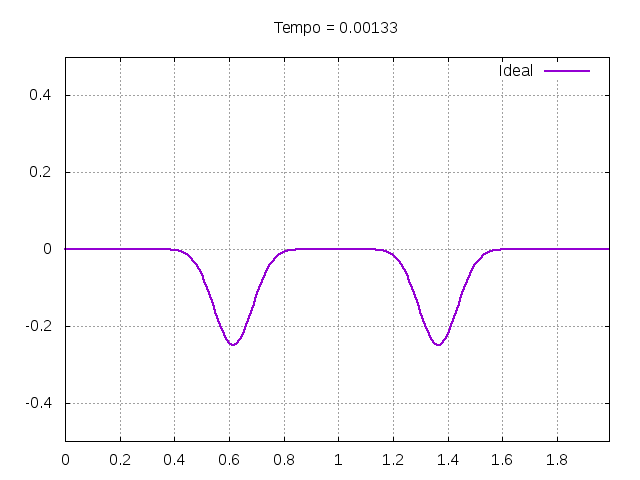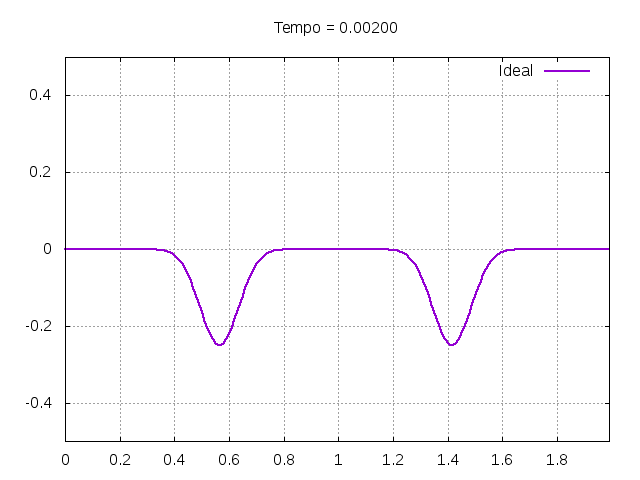
Corda C2:

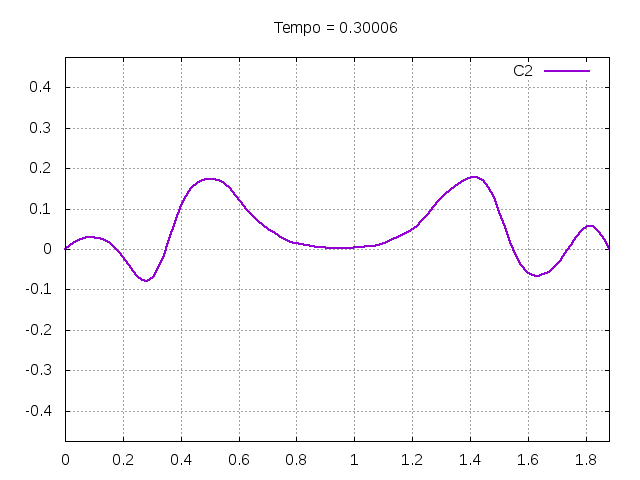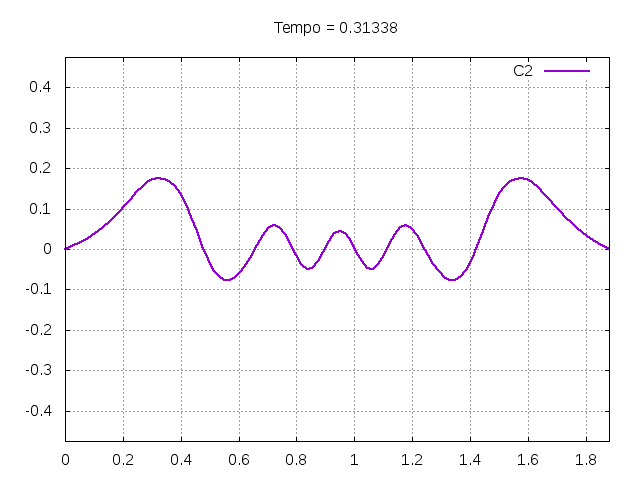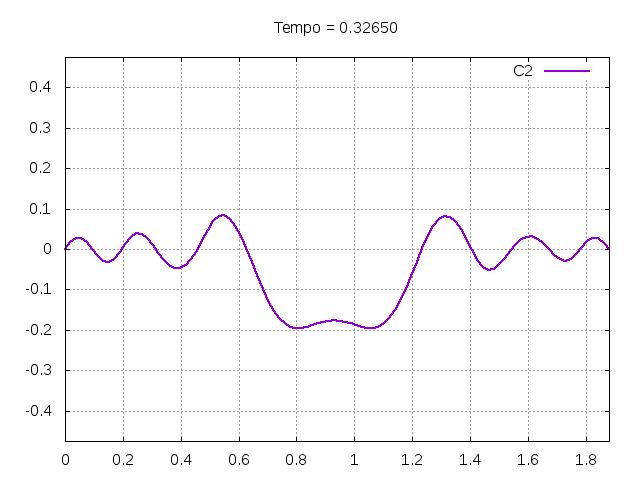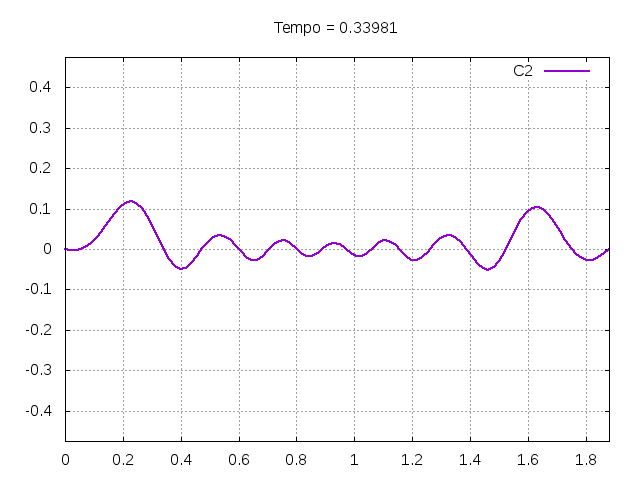
Corda C4:

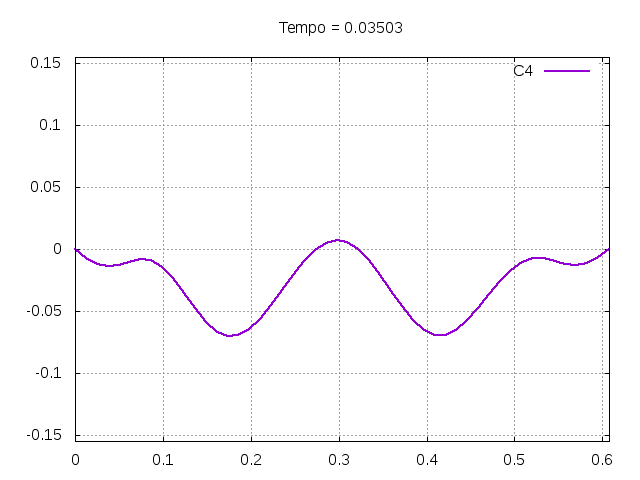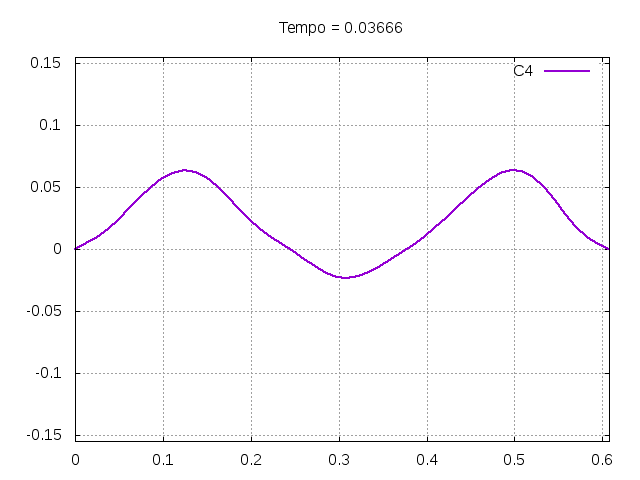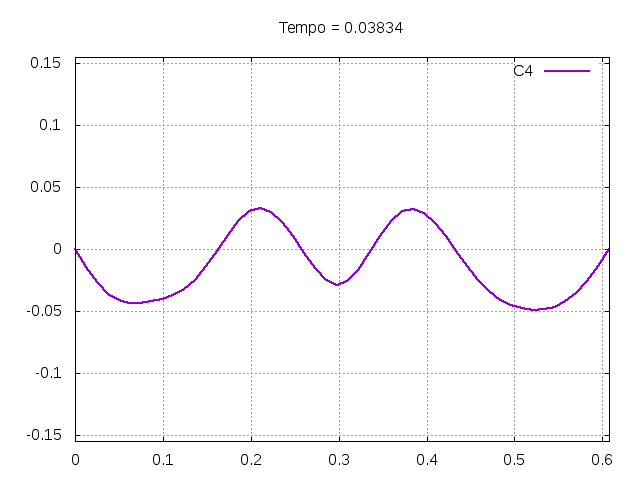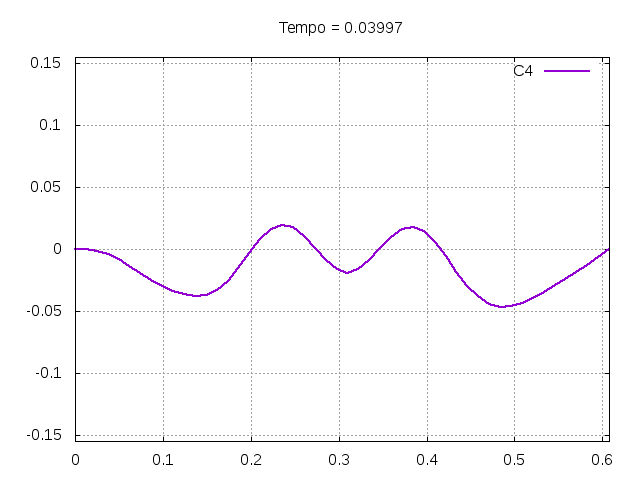
Corda C7:

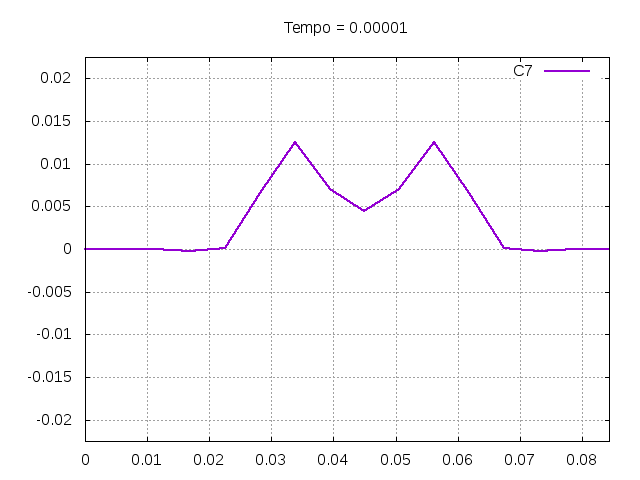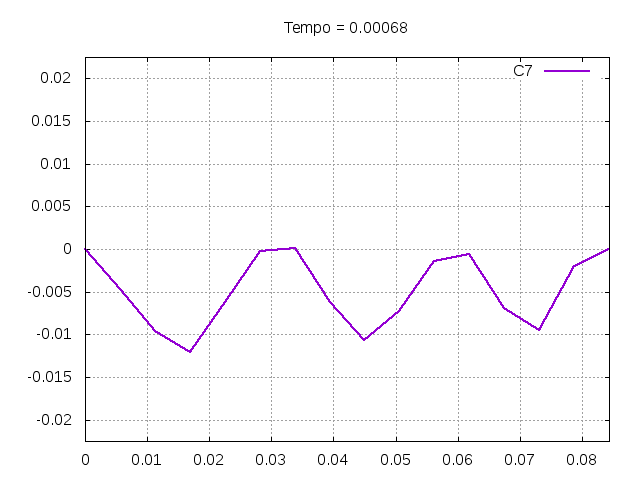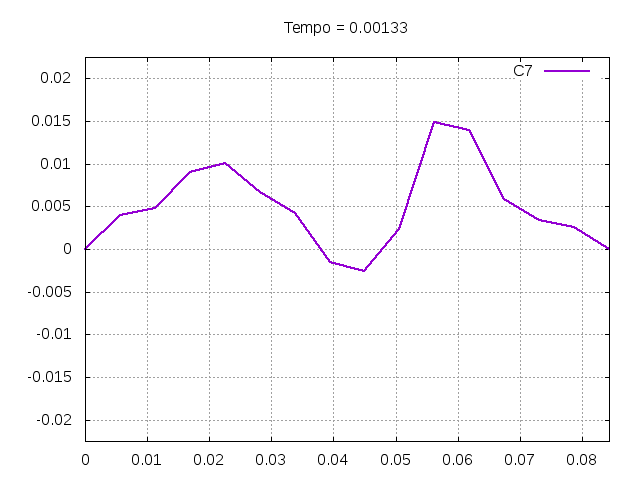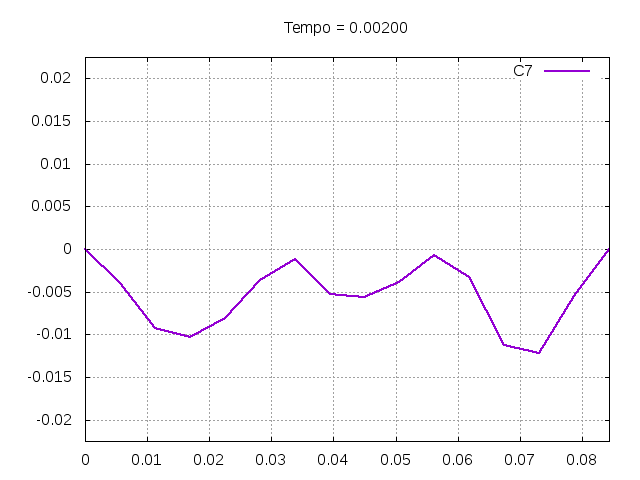
Análise de Erro e Estabilidade dos Métodos

Estabilidade do método Leapfrog

Pela estabilidade de Von Neumann, podemos escrever que

$r\leq 1.$

Para $r=1$, a equação da discretização da onda pode ser reescrita como

$U_{i}^{n+1}=U_{i+1}^{n}+U_{i-1}^{n}-U_{i}^{n-1}.$

Essa escolha com

${\frac {\Delta x}{\Delta t}}=c$

nos dá a solução exata sem dispersão numérica. Contudo, $r=1$ é válido somente no caso de uma corda ideal. É conveniente escrever a condição acima em termos da amostragem de sinal $f_{e}={\frac {1}{\Delta t}}$ e a frequência fundamental da corda $f_{1}={\frac {c}{2L}}$, o que nos leva a

$Kf_{1}\leq {\frac {f_{e}}{2}}$

O teorema de Nyquist diz que a frequência superior no espectro deve ser menor do que ${\frac {f_{e}}{2}}$ para evitar serrilhamento e para garantir uma reconstrução única e contínua. Logo, no caso ideal quando as autofrequências da corda são igualmente espaçadas ($\Delta f=f_{1}$), a condição de Nyquist indica que o número máximo de frequências no espectro é $K$. Isso significa que essa condição pode ser usada para selecionar o número apropriado de pontos espaciais $K$ para a corda. Entretanto, como $K$ é um inteiro, apenas valores discretos da frequência natural podem ser obtidos sem erros de trucamento, ou seja, usando $r=1$. Como series discretas não costumam ser utilizadas, precisamos aceitar pequenos erros de truncamento para ajustar $f_{1}$, ou seja, utilizando $r<1$. No caso de uma onda com fricção, temos que $r={\frac {1}{4}}$ é um valor de boa estabilidade.

Conclusões (?)

vsf caetano vsf doria vsf os dois vai tu anderson - dória aqui (mentira)

por favor usem U maiusculo com os indices i,n $U_{i}^{n}$ e não usem y, usem u minusculo

tem que aprender a fazer referência pras bib e colocar as bib aqui já dei up nos gif

flavia tu é muito linda flw vlw atri

---