Equação de Langevin

Artur Uhlik Fröhlich e Leonardo Dasso Migotto

O objetivo deste trabalho é resolver computacionalmente a equação de Langevin utilizando o método BAOAB. Serão explorados os casos de partículas individuais livres, estudando os efeitos da variação do coeficiente de atrito no deslocamento quadrático médio e no momentum médio.

Equação de Langevin

Esta equação diferencial estocástica descreve a evolução de um sistema quando sujeito a forças do tipo determinísticas e estocásticas simultâneamente. A sua aplicação mais popular é relativa ao movimento Browniano, o movimento de uma partícula macroscópica imersa em um fluído, sujeita à força de atrito excercida pelas partículas microscópicas do fluído. Neste caso, a equação pode ser escrita como:

{\frac {d{\vec {v}}}{dt}}=-\gamma {\vec {v}}+\xi (t).

Na equação acima, $\gamma$ é o coeficiente de atrito e $\xi (t)$ é um ruído estocástico branco, que segue o Teorema Central do Limite com média 0 e deslocamento padrão relacionado à temperatura, a Constante de Boltzmann, $\gamma$ e a massa da partícula. A partir desta expressão, é possível descobrir a relação do coeficiente de difusão do fluído e os valores envolvidos na equação:

D={\frac {2k_{B}T}{\gamma m}}.\quad (I)

Onde $D$ é o coeficiente de difusão do meio, $k_{B}$ é a constante de Boltzmann, $T$ é a temperatura e $m$ é a massa da partícula macroscópica. Outra relação presente no livro do Frenkel ^[1], desenvolvida analíticamente, é a do coeficiente de difusão e o deslocamento quadrático médio de uma partícula no meio:

\left\langle \left(r(t)-r_{0}(t)\right)^{2}\right\rangle =2dDt.\quad (II)

Método BAOAB

O método numérico escolhido para realizar a integração da equação é conhecido como BAOAB, desenvolvido por Leimkuhler e Mattews ^[2] utilizado para resolver equações diferenciais estocásticas.

Ele é baseado na solução exata para o momentum,

d{\vec {p}}=-\gamma {\vec {p}}dt+{\sqrt {2\gamma mk_{B}T}}d{\vec {W}},

e faz o uso de um método de separação das equações entre as denominadas A, B e O, respectivamente representadas:

{\vec {r}}\left(t+{\frac {\Delta t}{2}}\right)={\vec {r}}(t)+{\frac {\Delta t}{2}}{\vec {p}}\left(t+{\frac {\Delta t}{2}}\right){\frac {1}{m}},

{\vec {p}}\left(t+{\frac {\Delta t}{2}}\right)={\vec {p}}(t)+{\frac {\Delta t}{2}}{\vec {f}}(t),

{\vec {p'}}\left(t+{\frac {\Delta t}{2}}\right)=\exp(-\gamma \Delta t){\vec {p}}\left(t+{\frac {\Delta t}{2}}\right)+{\sqrt {1-\exp(-2\gamma \Delta t)}}{\sqrt {mk_{B}T}}{\vec {G}}.

O ${\vec {G}}$ aqui representa um número aleatório Gaussiano que faz o papel do ruído estocástico.

A equação "A" realiza meio passo no tempo da distância, a "B" realiza um meio passo para o momentum e o "O" contabiliza a contribuição estocástica equação.

Essas equações podem formar vários algoritmos de integração mas o utilizado nesse trabalho será o BAOAB:

{\vec {p}}\left(t+{\frac {\Delta t}{2}}\right)={\vec {p}}(t)+{\frac {\Delta t}{2}}{\vec {f}}(t),\quad (1)

{\vec {r}}\left(t+{\frac {\Delta t}{2}}\right)={\vec {r}}(t)+{\frac {\Delta t}{2}}{\vec {p}}\left(t+{\frac {\Delta t}{2}}\right){\frac {1}{m}},\quad (2)

{\vec {p'}}\left(t+{\frac {\Delta t}{2}}\right)=\exp(-\gamma \Delta t){\vec {p}}\left(t+{\frac {\Delta t}{2}}\right)+{\sqrt {1-\exp(-2\gamma \Delta t)}}{\sqrt {mk_{B}T}}{\vec {G}},\quad (3)

{\vec {r}}(t+\Delta t)={\vec {r}}\left(t+{\frac {\Delta t}{2}}\right)+{\frac {\Delta t}{2}}{\vec {p'}}\left(t+{\frac {\Delta t}{2}}\right){\frac {1}{m}},\quad (4)

{\vec {p}}(t+\Delta t)={\vec {p'}}\left(t+{\frac {\Delta t}{2}}\right)+{\frac {\Delta t}{2}}{\vec {f}}(t).\quad (5)

É importante lembrar que entre os dois últimos passos é necessário atualizar o termo ${\vec {f}}$ , já que ele pode depender de termos já atualizados como ${\vec {p}}$ ou ${\vec {r}}$ .

Implementação do Método BAOAB

Um exemplo de implementação desse método feito foi para a partícula livre. Nota-se que nesse caso a partícula não é afetada por um campo potencial então os passos do método que envolvem a força ${\vec {f}}$ serão desconsiderados.

A função a seguir se encontra em um código (orientado a objeto) de autoria do integrante Artur e que pode ser acessado aqui.

    def baoab_livre(self, dt, exp, sqexp, sqt, G):
        '''
        dt: discretização do tempo
        exp: termo referente a primeira exponencial da eq.3
        sqexp: termo da raiz quadrada com exponencial da eq.3
        sqt: termo da raiz quadrada com a Temperatura da eq.3
        G: o vetor G da eq.3
        '''
        # 1/2 passo da distância
        self.pos[0] += self.vel[0]*(dt/2)
        self.pos[1] += self.vel[1]*(dt/2)
        # Passo estocástico
        self.vel[0] = exp*self.vel[0] + sqexp*sqt*G[0]
        self.vel[1] = exp*self.vel[1] + sqexp*sqt*G[1]
        # Atualização final da posição
        self.pos[0] += self.vel[0]*(dt/2)
        self.pos[1] += self.vel[1]*(dt/2)

Essa função representa um passo do laço temporal utilizando o método BAOAB. Os atributos em forma de lista ".pos" e ".vel" representam as componentes x e y respectivamente da posição e velocidade do objeto partícula.

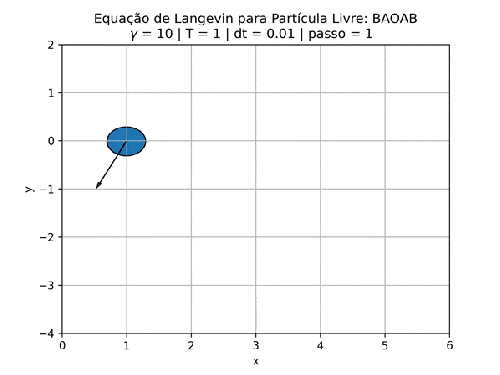
Um exemplo de funcionamento do código é a animação a seguir:

Simulação de uma partícula livre sob o efeito da Equação de Langevin.

O código foi executado usando a semente de números aleatórios 420.

Parâmetros das Simulações

A fim de estudar a implementação do Método BAOAB para a Equação de Langevin para uma partícula livre, nove simulações foram executadas com parâmetros bem definidos. Utilizando unidades reduzidas, os parâmetros recebidos pelo computador foram:

m,k_{B}=1

,

\Delta t=10^{-2}

,

t_{max}=5\cdot 10^{5}

,

{\vec {r}}_{ini}=(0,0)

,

{\vec {p}}_{ini}=(0,0)

,

\gamma =10^{-1},10^{0},10^{1}

,

T=1,2,3

.

As nove simulações englobam, ao todo, todas combinações de $T$ e $\gamma$ para os valores escolhidos. Após todos os $50.000.001$ instantes da simulação serem calculados, o computador salva os valores de posição e momentum de cada um deles em arquivos numa pasta única, que contem, além destes valores, os valores utilizados na simulação. Assim, um programa diferente pode ser utilizado para continuar a execução da simulação ou também gerar gráficos dos valores salvos de posição e momentum. Isso permite uma análise facilitada dos dados, pois não requer a execução completa do programa para cada gráfico que se deseja criar.

Como esta é uma simulação com uma variável estocástica, alguns cuidados são extremamente importantes para fazer a execução correta da simulação. Os seguintes fatos devem ser tidos em mente ao executar simulações desta natureza:

- As simulações devem sempre possuir sementes aleatórias diferentes, com pouquíssimas exceções. Utilizando os nossos programas de exemplo: caso os valores de

T

e

\gamma

fossem trocados, mas a semente aleatória não, estaríamos utilizando os mesmos valores aleatórios para calcular o termo estocástico da equação, não gerando simulações completamente independentes. Além do mais, a "grande sacada" dessas simulações é que elas devem conseguir ser analisadas independente das sementes aleatórias.

- Simulações com

\Delta t

diferentes, porém todas outras variáveis iguais (incluindo a semente aleatória) não são equivalentes. Utilizando os nossos programas de exemplo: caso o

\Delta t

mude, o número de números aleatórios a ser gerado será diferente, portanto ambas simulações, aparentemente equivalentes, terão ruídos aleatórios completamente diferentes e, portanto, não poderão ser comparadas tradicionalmente.

Implementação da Graficação do Momentum

Segue abaixo uma implementação de um graficador do histograma normalizado do momenta de uma partícula. A partir de um array de momenta de uma única partícula, o código faz os cálculos necessários, deixando o gráfico pronto para plotagem.

A função a seguir se encontra em um código de autoria do integrante Leonardo. Este código abre os dados gerados por outro programa, que salva todas informações em arquivos, e permite visualizar propriedades como o MSD, a distribuição do momentum, entre outras coisas.

if modo == "P":
    p = np.sqrt(pxy[:, 0]**2 + pxy[:, 1]**2)
    #MOMENTUM MAIS COMUM
    n, bins, patches = plt.hist(p, 500, histtype = "step",  density = True)
    maior = np.argmax(n)
    pcomum = (bins[maior + 1] + bins[maior])/2
    plt.axvline(pcomum, color = "red", alpha = 0.4, label = f"Momentum mais provável: {pcomum:.3f}")
    #MOMENTUM MEDIO
    pmed = np.mean(p)
    plt.axvline(pmed, c = "green", label = f"Momentum médio: {pmed:.3f}")
    #MOMENTUM QUADRADO MEDIO
    pqmed = np.sqrt(np.mean(p**2))
    plt.axvline(pqmed, color = "purple", alpha = 0.4, label = f"Momentum rms: {pqmed:.3f}\n" + r"$\frac{p_{rms}}{\sqrt{T}}$" + f": {pqmed/np.sqrt(temp):.3f}")
    plt.xlim(0, 7)
    plt.ylim(0, 0.7)
    plt.grid(alpha = 0.3)
    plt.legend(loc = 1)
    plt.title(f"Momentum em módulo\n" + r"$\gamma$ = " + f"{gaminha}, Temp. = {temp}, " + r'$\Delta t$ = '+f'{dt}, Instantes = {nsalvos}')
    plt.ylabel(r'$P(x)$')
    plt.xlabel(r'$\left|\vec{p}(t)\right|$')

Neste código, "pxy" é um array bidimensional, onde os índices da primeira dimensão representam o tempo, e a segunda dimensão possui dois índices: um para o momentum em $x$ e outro para o momentum em $y$ . O programa calcula o módulo do momentum, além de outros três valores (decididos durante as plotagem de testes por conta dos aspectos iniciais dos gráficos): o momentum mais provável, o momentum médio e a média do momentum quadrático (além de um cálculo dele relacionado à temperatura). Um histograma normalizado dos momenta é feito simultâneo ao cálculo do momentum mais provável, além de ajustes de elementos gráficos do gráfico. Por ser um histograma normalizado, ele segue a seguinte relação (onde $p(x)$ é a função da curva do gráfico):

$\int _{0}^{+\infty }P(x)dx=1.$

Análise do Momentum

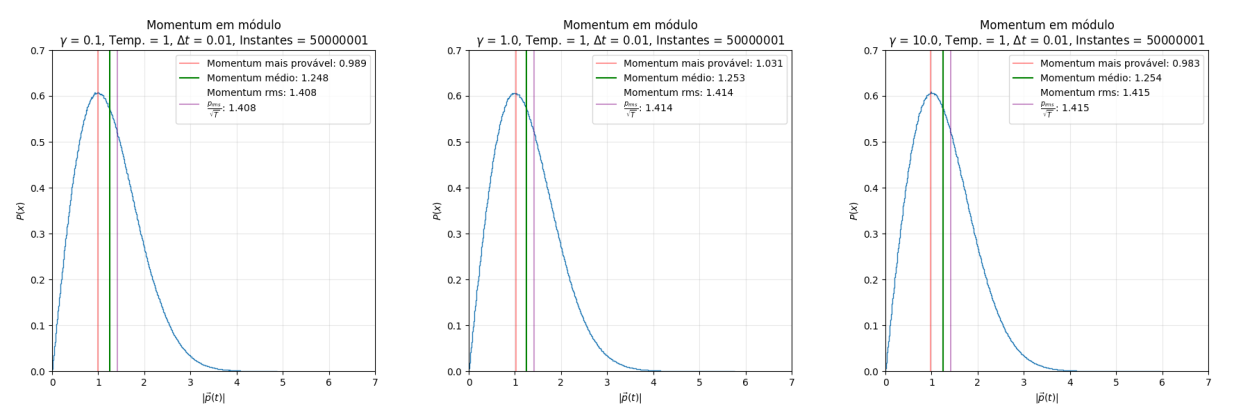
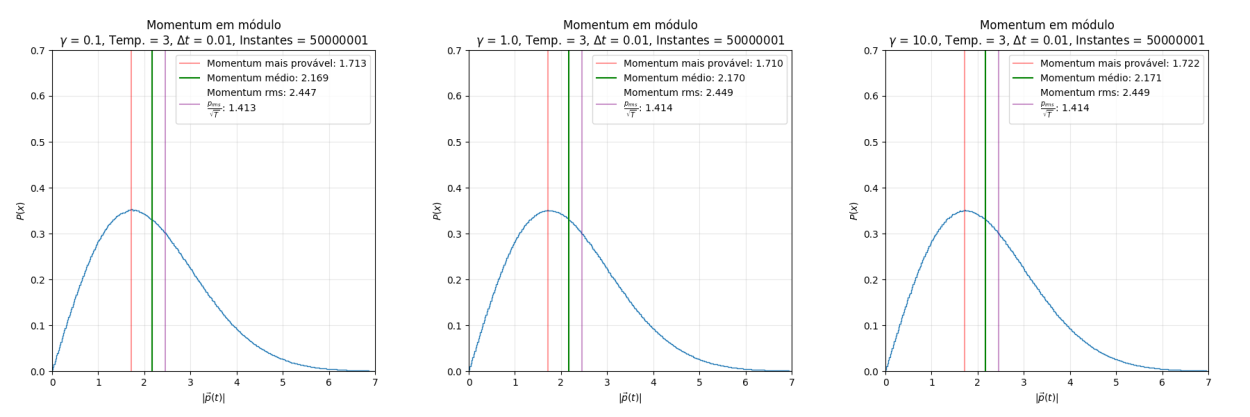
Os gráficos abaixo, gerados pelo código acima, mostram a densidade de probabilidade de, escolhido um instante aleatório da simulação, qual momentum a partícula possui.

T=1,\gamma =0.1,1.0,10

T=2,\gamma =0.1,1.0,10

T=3,\gamma =0.1,1.0,10

Uma observação rápida dos gráficos (mesmo que ignorando as retas destacadas na plotagem e as informações da legenda) torna evidente que a distribuição em questão é a Maxwell-Boltzmann. Esta distribuição descreve a densidade de probabilidade da velocidade das moléculas de um gás em equilíbrio térmico. Dado que, utilizando $m=1$ , o valor de momentum e de velocidade são iguais em módulo, é coerente que esta distribuição apareça para o momentum. Como é característico da distribuição de Maxwell-Boltzmann, a temperatura "estende" o limite da função, diminuindo seu pico. Para comprovar a relação da temperatura com a distribuição, podemos utilizar (como já foi feito nos gráficos) a fórmula da $V_{rms}$ :

$V_{rms}={\sqrt {\frac {3RT}{M}}}.$

Como está em evidência nos gráficos anteriores, retirar a proporção da raiz da temperatura dos valores de $P_{rms}$ (que, como discutimos anteriormente, possui valor equivalente ao $V_{rms}$ ) retorna sempre o mesmo valor.

Implementação do Deslocamento Quadrático Médio

Segue abaixo uma implementação do cálculo do deslocamento quadrático médio. A partir de um array de posições de uma única partícula, o código faz os cálculos necessários retornando um array com o MSD em cada instante de tempo, além de outras coisas.

A função a seguir se encontra em um código de autoria do integrante Leonardo. Este código abre os dados gerados por outro programa, que salva todas informações em arquivos, e permite visualizar propriedades como o MSD, a distribuição do momentum, entre outras coisas.

if modo == "MSD":
    novotamanho = int(1 + ((nsalvos-1)/divisoes))
    desviodividido = np.zeros(novotamanho)
    indice = novotamanho - 1
    xx = xy[:, 0]
    yy = xy[:, 1]
    for i in range(divisoes):
        xini = xx[i*indice]
        yini = yy[i*indice]
        dx = xx[i*indice : 1+(i+1)*indice] - xini
        dy = yy[i*indice : 1+(i+1)*indice] - yini
        desviodividido += dx**2 + dy**2
    desviodividido = (desviodividido/divisoes)[1:]
    eixox = np.linspace(0, int(tmax/divisoes), int((nsalvos - 1)/divisoes) + 1)[1:]
    difusivo = desviodividido[int(10/(dt*gaminha)):]
    dezao = np.mean(difusivo/eixox[int(10/(dt*gaminha)):])/4
    eixox = np.log10(eixox)
    desviodividido = np.log10(desviodividido)
    balistico = desviodividido[:int(1/(dt*gaminha))]
    difusivo = desviodividido[int(10/(dt*gaminha)):]
    bal = np.polyfit(eixox[:int(1/(dt*gaminha))], balistico, 1)
    dif = np.polyfit(eixox[int(10/(dt*gaminha)):], difusivo, 1)
    reta1 = bal[0]*eixox + bal[1]
    reta2 = dif[0]*eixox + dif[1]

Neste código, "xy" é um array bidimensional, onde os índices da primeira dimensão representam o tempo, e a segunda dimensão possui dois índices: um para a posição em $x$ e outro para a posição em $y$ . Para melhorar a precisão do MSD, o programa permite "fatiar" o array original de posições, considerando cada fatia das distâncias como uma execução do programa independente (o número de fatias é a variável "divisoes", definida ao iniciar o programa). Um número maior de fatias resulta em um tempo reduzido percorrido pela partícula em cada fatia, porém retorna dados com maior precisão.

Após definir a posição relativa de cada fatia dentro do array original, o programa itera sobre ele, calculando os valores de MSD para cada instante de cada fatia e somando-os a um array vazio. Por fim, é feito a média dos MSDs pelo número de partículas neste array. Dado o modo preferido de visualizar os dados posteriormente e a necessidade de outras análises numéricas, o array é transformado para escala logarítmica. É importante destacar que, antes de transformar os arrays de tempo e MSD para a escala logarítmica, ambos perdem o valor de índice 0: isso é importante pois, ao transformar os tempos para esta escala, o valor do $Log_{10}0=-\infty$ , e este valor é impossível de ser calculado computacionalmente.

Em seguida, dois arrays criados a partir do do MSD: um deles contém somente pontos do período de difusão balística, enquanto o outro possui pontos da difusão normal. É feita a regressão linear de cada um destes conjuntos de dados, a fim de encontrar a inclinação das retas ajustadas aos dados (e confirmar que estes períodos possuem, de fato, essas características difusivas, como veremos a seguir). Os intervalos para os períodos de difusão foram escolhidos após uma análise interna dos gráficos.

Estas informações são posteriormente colocadas em um gráfico utilizando outras funções. Estes gráficos poderão ser vistos na próxima seção.

Análise do MSD

Os resultados a serem analisados são originados do código (procedural) do integrante Leonardo.

Foram executadas diferentes vezes a simulação para compararmos a influência do $\gamma$ e da temperatura no deslocamento quadrático médio:

\gamma =0.1,T=1,2,3

\gamma =1.0,T=1,2,3

\gamma =10,T=1,2,3

De início pode-se notar que o ${\vec {r^{2}}}$ escala de maneira proporcional a $t^{2}$ (balístico) no início do processo, e depois de um determinado tempo obtemos uma relação linear que é a parte difusiva do processo. Essas inclinações das retas nos regimes balístico e difusivo são constantes em relação ao $\gamma$ e à temperatura. Outro aspecto constante é a temperatura, que não gera aparente diferença nos gráficos de MSD (mas no valor do coeficiente de difusão sim)

Uma referência da literatura a respeito do MSD (mas no contexto de dinâmica molecular usando o potencial de Lennard-Jones) se encontra no livro do Frenkel, expressa por essa imagem:

A partir da figura pode-se notar que a inclinação das retas representantes dos regimes balístico e difusivo são 2 e 1, valores esses encontrados pelas simulações realizadas.

Outro aspecto importante a se ressaltar é a concordância do cálculo do coeficiente de difusão através da equação (I) e da relação de Einstein em (II), obtida através dos pontos presentes na parte difusiva.

Uma relação interessante encontrada foi a maneira como escala a mudança de regimes, indicada pela reta perpendicular ao eixo do tempo. Podemos encontrar uma aproximação para o tempo em que o regime difusivo inicia na simulação a partir de uma relação dependente de $\gamma$ :

\Omega \propto {\frac {1}{\gamma }}

Referências

↑ Daan Frenkel and Berend Smit. 2001. Understanding Molecular Simulation (2nd. ed.). Academic Press, Inc., USA.
↑ Leimkuhler, B., & Matthews, C. (2015). Molecular Dynamics: With Deterministic and Stochastic Numerical Methods. (Interdisciplinary Applied Mathematics; Vol. 39). Springer. https://doi.org/10.1007/978-3-319-16375-8

[1] Daan Frenkel and Berend Smit. 2001. Understanding Molecular Simulation (2nd. ed.). Academic Press, Inc., USA.

[2] Leimkuhler, B., & Matthews, C. (2015). Molecular Dynamics: With Deterministic and Stochastic Numerical Methods. (Interdisciplinary Applied Mathematics; Vol. 39). Springer. https://doi.org/10.1007/978-3-319-16375-8

[1]

[2]

Equação de Langevin

Índice