Modelo de Potts - 2D

O Modelo

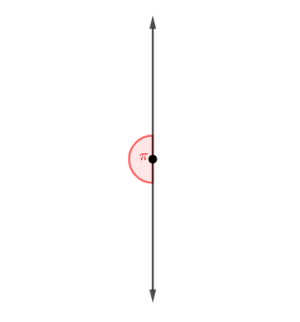
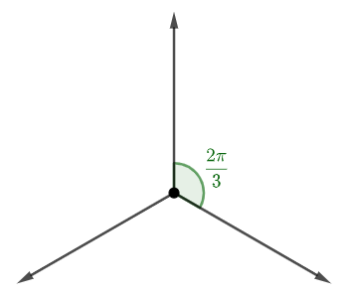
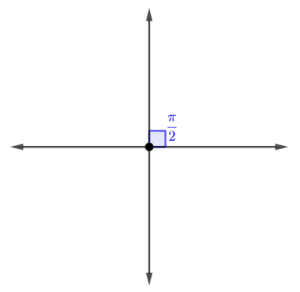
Modelo de Potts pode ser considerado uma generalização do Modelo de Ising. Enquanto no Ising, os spins podem assumir valores $1$ ou $-1$, no Modelo de Potts, os spins podem assumir valores que dependem de uma variavél $Q$ da seguinte forma: $\theta _{n}={\frac {2\pi n}{Q}}$. A quantidade $\theta _{n}$ nos fornece as possíveis orientações para os spins. Os valores que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} pode assumir são Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=1,2,3,...,Q} . Dessa forma, um Modelo de Potts bidimensional com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q=10} possui uma rede bidimensional de spins com 10 orientações diferentes.

Possibilidades de spin para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q=2} .

Possibilidades de spin para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q=3} .

Possibilidades de spin para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q=4} .

O Hamiltoniano de interação, na ausência de campo magnético, pode ser escrito como

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_p = -J \sum_{(i,j)} \delta(s_i,s_j) }

onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J} é a constante de acoplamento que determina a intensidade da interação e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta(s_i,s_j) } é a delta de Kronecker, definida como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_i=s_j} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_i\neq s_j} .

Relação com o Modelo de Ising

O Modelo de Ising é obtido quando tomamos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle q=2} na expressão para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_n} .

O Hamiltoniano de Ising pode ser escrito como o Hamiltoniano do Potts mais uma constante aditiva Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_I = H_p + \sum_{(i,j)}\frac{J}{2} = -J\sum_{(i,j)} \delta(s_i,s_j) + \sum_{(i,j)}\frac{J}{2} = -\frac{J}{2}\sum_{(i,j)} [2\delta(s_i,s_j) - 1]}

Se incluirmos o campo magnético, o Hamiltoniado de Potts fica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_p = -J \sum_{(i,j)} \delta(s_i,s_j) - \sum_i \frac{1}{\beta} h_i s_i}

Algoritmo de Metropolis

Vamos implementar o Modelo de Potts utilizando o algoritmo de Metropolis.

O algoritmo de Metropolis é um método de Cadeia de Markov Monte Carlo (MCMC) para obter amostras aleatórias a partir de uma distribuição de probabilidade da qual a amostragem direta é difícil. O procedimento para a implementação do algoritmo é apresentado abaixo.

1. Inicialize

a) Escolha um estado inicial Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} ;

b) Coloque Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=0}

2. Itere

a) Gere um estado candidato aleatório Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x'} de acordo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x'|x_t)}

b) Calcule a probabilidade de aceitação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x',x_t) = min \left(1,\frac{P(x')}{P(x_t)} \frac{g(x_t | x')}{x'|x_t} \right)}

c) Aceite ou rejeite:

1) Gere um número aleatório uniforme Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u \in [0,1]} ;

2) E se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u\leq A(x',x_t)} , aceite o novo estado e defina Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{t+1}=x'} ;

3) E se Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle u>A(x',x_t)} , rejeite o novo estado e copie o estado antigo para frente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{t+1}=x_t} ;

4) Incremente: coloque t = t + 1

Em nosso caso, a distribuição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{A(x,x')}{A(x',x)}} será Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-\beta \Delta E}} , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta E=E_{x'} - E_{x}} .

Resultados das simulações

Definimos um Monte Carlo Step (MCS) como sendo o tempo em que a rede bidimensional com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2} spins é percorrida pelo algoritmo. Ao final de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2} flips de spin (seja com probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} ou com probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \exp(-\beta \Delta E)} ), contamos um MCS. Além disso, em todas as simulações, utilizamos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T=1} em unidades de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B} .

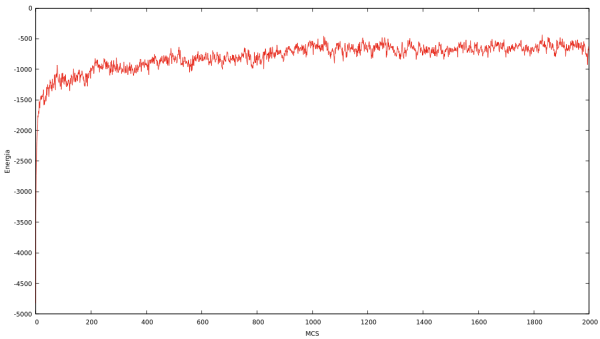
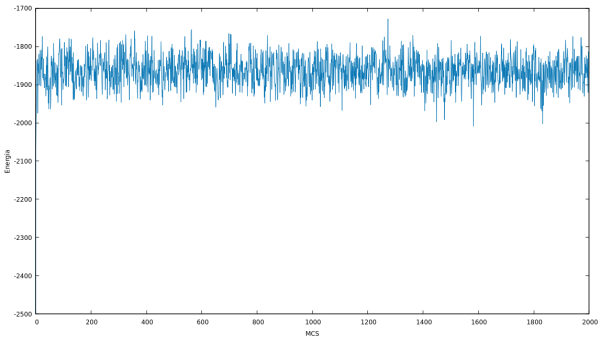
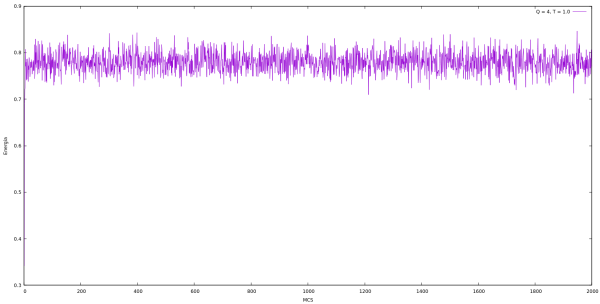
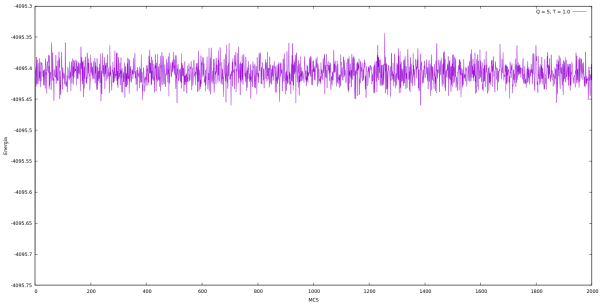
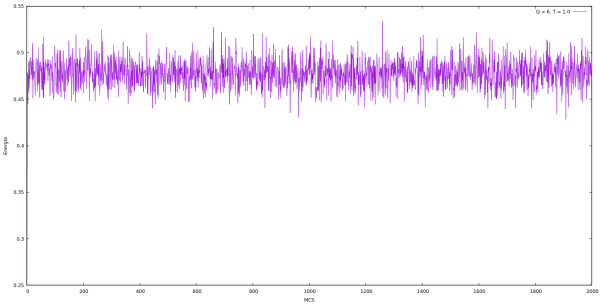
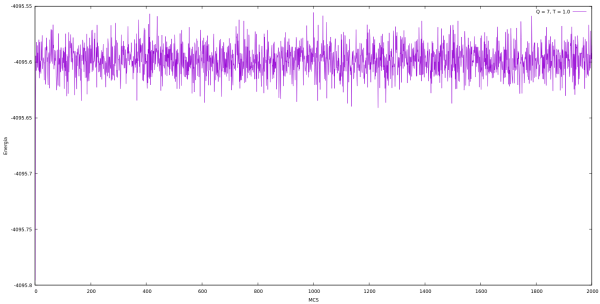
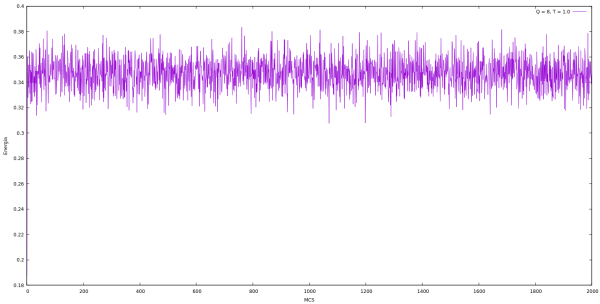
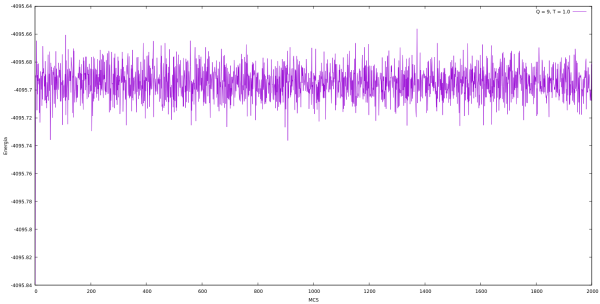
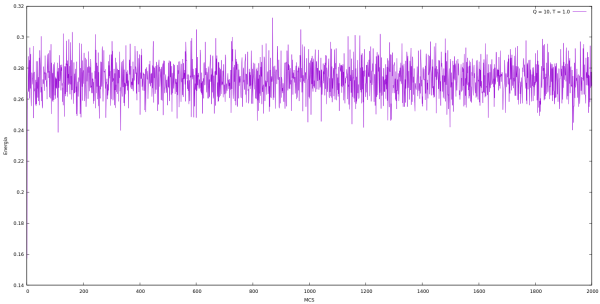
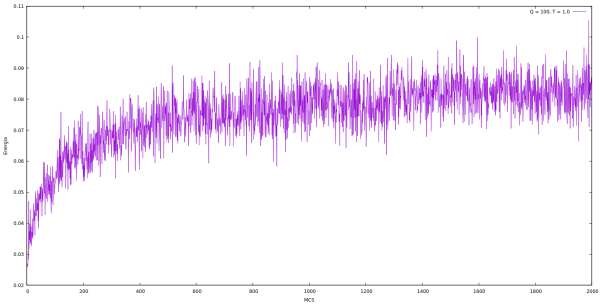
Energia

Energia em cada MCS para Q indo de 2 até 10 e L = 64 utilizando o algoritmo de Metropolis.
Energia média por MCS para Q = 2 e L = 64.	Energia média por MCS para Q = 3 e L = 64.
Energia média por MCS para Q = 4 e L = 64.	Energia média por MCS para Q = 5 e L = 64.
Energia média por MCS para Q = 6 e L = 64.	Energia média por MCS para Q = 7 e L = 64.
Energia média por MCS para Q = 8 e L = 64.	Energia média por MCS para Q = 9 e L = 64.
Energia média por MCS para Q = 10 e L = 64.	Energia média por MCS para Q = 100 e L = 64.

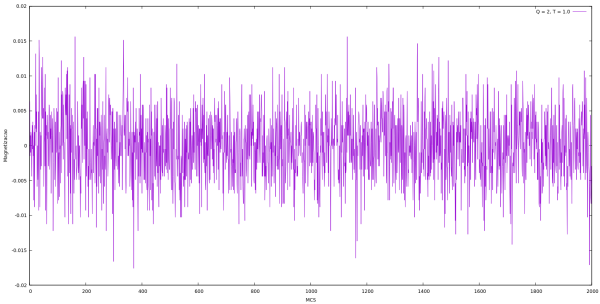
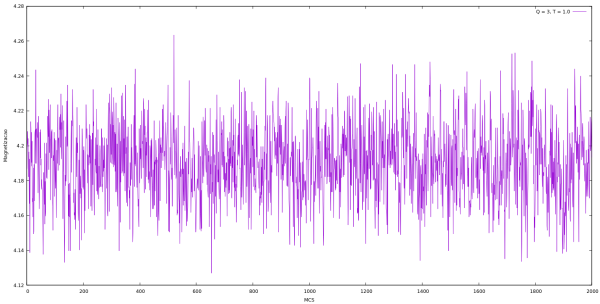
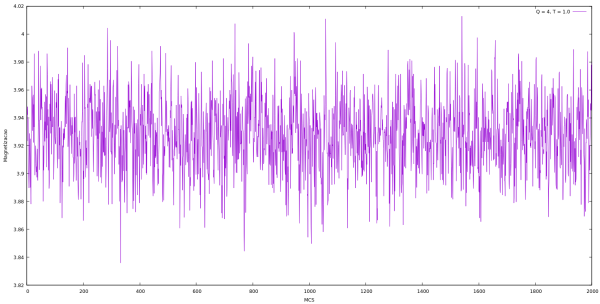
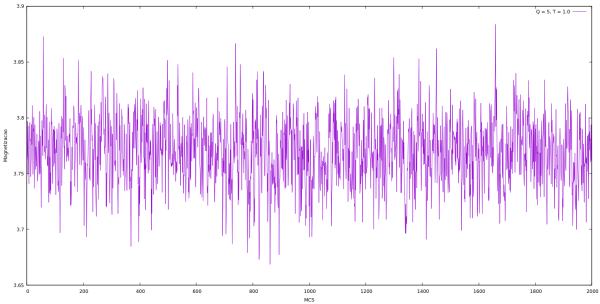
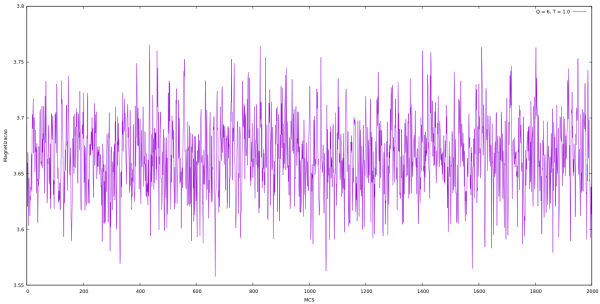
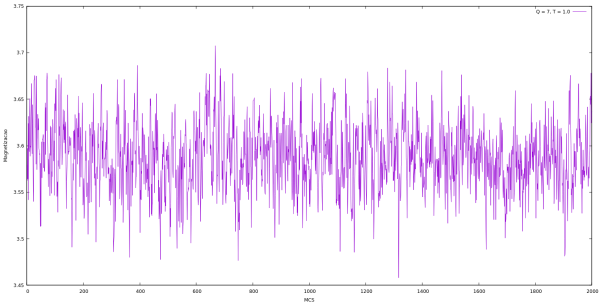
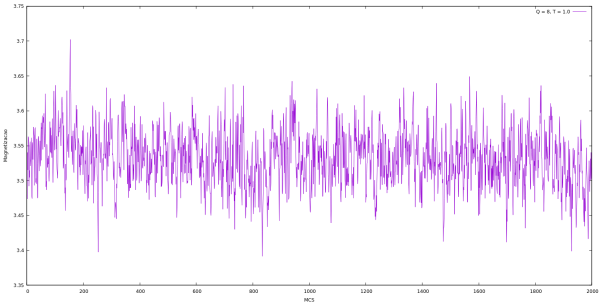
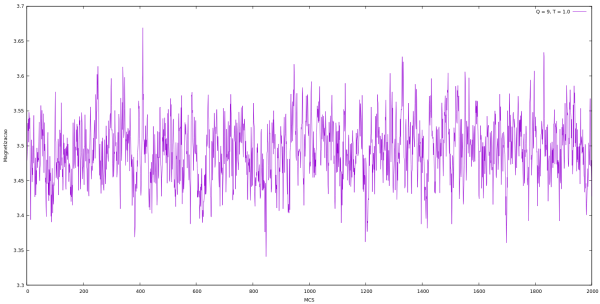
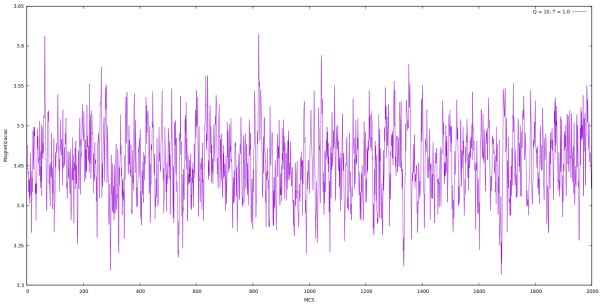
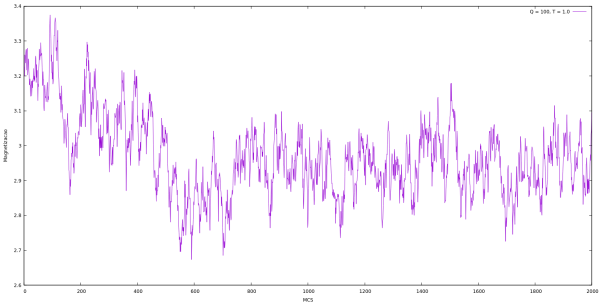
Magnetização

Magnetização em cada MCS para Q indo de 2 até 10 e L = 64 utilizando algoritmo de Metropolis.
Magnetização média por MCS para Q = 2 e L = 64.	Magnetização média por MCS para Q = 3 e L = 64.
Magnetização média por MCS para Q = 4 e L = 64.	Magnetização média por MCS para Q = 5 e L = 64.
Magnetização média por MCS para Q = 6 e L = 64.	Magnetização média por MCS para Q = 7 e L = 64.
Magnetização média por MCS para Q = 8 e L = 64.	Magnetização média por MCS para Q = 9 e L = 64.
Magnetização média por MCS para Q = 10 e L = 64.	Magnetização média por MCS para Q = 100 e L = 64.

Códigos utilizados

O código foi escrito em Fortran.

Metropolis - Potts 2D

Referências

D. P. Landau, K. Binder. A Guide Monte Carlo Simulations in Statistical Physics. Cambridge University. New York. 2000.

L. M. Barone, E. Marinari, G. Organtini, F. Ricci-Tersengui. Scientific Programming: C-Language, Algorithms and Models in Science. World Scientific. Singapore. 2013.