Modelo de agentes de distribuição de riquezas
Grupo: Bernardo Boatini, Murilo Kessler Azambuja e Natália Ferrazzo
Introdução
A física estatística, em particular a teoria cinética dos gases, fornece uma estrutura útil para descrever a complexidade das interações de mercado. Da mesma forma que um sistema físico composto de muitas partículas trocando energia via colisões binárias, os Modelos de Troca de Cinética consideram um conjunto de agentes econômicos interagentes que trocam de forma binária uma quantidade conservada chamada de riqueza.
Este trabalho tem como objetivo calcular a evolução temporal da distribuição de riqueza entre entre um certo numero de agentes, utilizando diferentes regras de interação e um critério para medir quantitativamente a desigualdade econômica no sistema.
Modelo
Vamos supor um sistema com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} agentes, onde o agente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} é caracterizado pela riqueza Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_i(t)} e pelo fator de aversão a risco Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_i} no tempo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} . Podemos então definir uma troca de riqueza entre os agentes Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} selecionados aleatoriamente, supondo que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} ganha uma riqueza Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta w} de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} , como [1]
Em modelos de trocas binárias como esse, quando a regra não favorece nenhum dos lados, já foi demonstrado analíticamente que o estado final sempre leva a condensação de riqueza em um agente[2], ou seja, máxima desigualdade. Para pensar formas de evitar a condensação, certas dinâmicas podem ser adicionadas ao problema, como, por exemplo, definir uma maior probabilidade do agente mais pobre ganhar na troca.
Para decidir quem ganha e quem perde riqueza durante a interação entre agentes, utiliza-se uma probabilidade de favorecer o agente mais pobre, evitando assim a condensação, i.e., o acúmulo de toda riqueza disponível em apenas um ou poucos agentes [1]. Esta probabilidade é dada por [1] [3]
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} é chamado de fator de proteção social, que varia de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} —mesma probabilidade de ganho de riqueza para ambos os agentes— até Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/2} —máxima probabilidade de favorecer o agente mais pobre. Desta forma, a probabilidade do agente mais pobre ganhar a quantidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta w} em uma interação entre agentes é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} , enquanto que a probabilidade do agente mais rico ganhar a mesma quantidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta w} é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1-p} . Além disso, vemos na equação (1) que quanto maior a desigualdade de riqueza (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_i(t)-w_j(t)} ), maior é a atuação de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} . Isso nos mostra que o fator de proteção social é uma forma de simular a aplicação políticas sociais que favorecem a distribuição de renda na população.
Uma vez sorteado qual 2 agentes, deve-se determinar qual será a quantidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta w} a ser trocada por ambos. Existem diversas formas(regras de troca) de executar essa transferencia de riqueza (algumas delas encontram-se de forma detalhada em [2]). Porém neste trabalho focaremos apenas em dois tipos de regra: na regra do mínimo e na regra do perdedor, enunciadas abaixo.
Regra do Mínimo
Nesta regra, temos que a quantidade de riqueza trocada entre os agentes é definida como [4]
Esta regra muitas vezes também é chamada de regra justa, pois a quantidade de riqueza trocada entre os agentes é a mesma, independente do ganhador, logo nenhum dos agentes é favorecido.
Regra do Perdedor
Neste caso, para tentar evitar condensações, temos que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta w} é obtido apenas pela quantia arriscada pelo perdedor, desta forma temos [4]
lembrando que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} é o agente perdedor. Desta forma, a quantidade de riqueza a ser trocada será sempre proporcional à fortuna de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} (i.e., Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_j(t)} ) e regulada por quanto o agente está disposto a arriscar (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_j} ), tornando a interação entre os agentes muito mais favorável para o perdedor.
Coeficiente de Gini
O Coeficiente de Gini é um índice frequentemente utilizado por economistas e organizações estatísticas para mensurar quantitativamente a desigualdade de distribuição de renda em uma determinada região. Ele é definido como [1]
O índice de Gini varia de 0, quando todos os agentes possuem a mesma riqueza (i.e., desigualdade mínima), até 1, quando toda riqueza está concentrada em apenas um agente (i.e, desiguladade máxima). Este coeficiente é utilizado tanto para medir a desigualdade na distribuição de renda dos agentes da simulação, quanto como uma medida de dispersão, para determinar a estabilidade da distribuição de riqueza [1].
Resultados
Como unidade de tempo das simulações foi utilizado o MCS (Monte Carlo Step), definido como o menor número de passos necessários para que todos os agentes sejam sorteados[1]
Evolução temporal sem fator de proteção social
Na Figura 1 e na Figura 2 temos a evolução temporal do coeficiente de Gini para a regra do perdedor e para a regra do mínimo, respectivamente. Estas simulações foram realizadas com um número de agentes Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = 10000} sob uma média sob 10 condições inicias diferentes(ensembles) para cada valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} . As condições iniciais foram tais que a riqueza (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_i} ) está inicialmente distribuída no intervalo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0,1]} seguindo uma distribuição aleatória uniforme.
Note que após um certo número de MCS, o índice de Gini tende a convergir para um valor estável, para cada valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} . O tempo de simulação foi escolhido de forma que o equilíbrio fosse atingido. O primeiro MCS foi ignorado para melhor visualização das curvas em escala, já que o interesse é no estado estacionário.
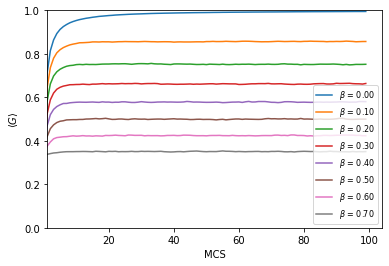

Na Figura 2, vemos que o valor de estabilidade do índice de Gini sempre tende para o valor de desigualdade máxima, mesmo se mudarmos o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} . Desta forma, quando não inserimos um fator de proteção social no problema e assumimos que as trocas entre agentes ocorrem segundo a regra do mínimo, teremos sempre uma condensação da riqueza, levando a uma alta desigualdade econômica.
Por outro lado, na Figura 1, vemos que quanto maior for o fator de aversão ao risco, menor será a desigualdade econômica e apenas quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = 0} ocorre condensação (indicando, pela equação (3), que em cada interação os agentes irão trocar toda a riqueza disponível para eles).
Este resultado (a regra do mínimo sempre gerar uma condensação enquanto que a regra do perdedor estabiliza em um valor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle < 1} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta>0} ) ocorre pois, como o valor de beta é igual para todos os agentes, teremos que, por (3), os agentes com maior riqueza irão perder mais dinheiro na regra do perdedor do que os agentes com menor riqueza e, desta forma, a riqueza estará mais bem distribuída quando o equilíbrio for atingido. Por outro lado, como na regra do mínimo o valor trocado independe de quem perde, se forem sorteados agentes com uma diferença muito grande de riqueza teremos que, por (2), a quantidade de riqueza perdida pelo agente mais pobre será muito maior comparativamente com sua própria riqueza. Desta forma teremos que, após tempo suficiente, a regra do mínimo sempre irá tender para uma distribuição de renda desigual.
Nas Figuras 3 e 4, temos outra evolução temporal do Índice de Gini. Nestes casos, as simulações foram realizadas com número de agentesFalhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} igual a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 20000} (para uma obter um gini mais estável) sob uma média de 10 ensembles, assim como as anteriores. Além disso, as condições iniciais foram tais que tanto a riqueza (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_i} ) quanto o fator de aversão ao risco (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_i} ) foram inicialmente distribuídas no intervalo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0,1]} seguindo uma distribuição aleatória uniforme. Desta forma podemos obter um resultado mais realista, onde cada agente tem um Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_i} diferente e aleatório.
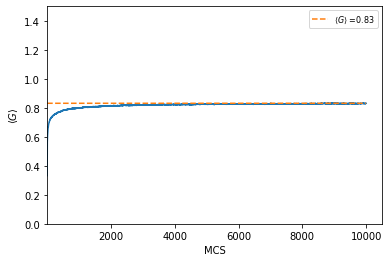
Na Figura 3, assim como na Figura 2, vemos que, apesar de não ter nenhum fator de proteção social, a distribuição de riqueza estabiliza em um valor menor do que 1, exatamente por que na regra do perdedor os agentes com maior riqueza arriscam perder mais do que arriscam em ganhar.
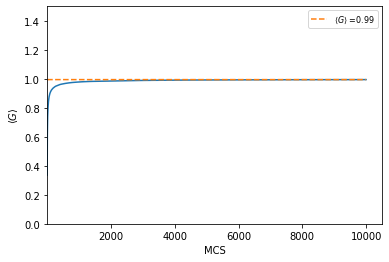
Na Figura 4, vemos a mesma tendência observada anteriormente quando a regra do mínimo foi utilizada, i.e., o equilíbrio tende para uma condensação. Isto ocorre pelo mesmo motivo anteriormente discutido: quando eventualmente ocorrer uma troca entre dois agentes com uma diferença de riqueza considerável, o agente mais pobre irá perder muito mais comparativamente a sua riqueza, devido à equação (2). Desta forma, depois de passado uma quantidade de tempo suficiente, toda riqueza vai estar concentrada em muito poucos agentes.
Evolução temporal com fator de proteção social
As simulações que serão apresentadas abaixo foram realizadas com um número de agentes Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = 10000} sob uma média entre 10 ensembles diferentes para cada valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} . As condições iniciais em todas simulações foram tais que a riqueza (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w_i} ) e a aversão ao risco (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta(i) } ) estão distribuídas no intervalo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0,1]} seguindo uma distribuição aleatória uniforme (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta(i) } permanece constante durante toda simulação).
Na Figura 5 e na Figura 6 temos a evolução temporal do coeficiente de Gini para a regra do perdedor(a esquerda) e para a regra do mínimo(a direita). Para cada valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} , note que após um certo número de MCS o índice de Gini tende a convergir para um valor estável, se tomamos um tempo de simulação suficientemente grande (o primeiro MCS foi ignorado).
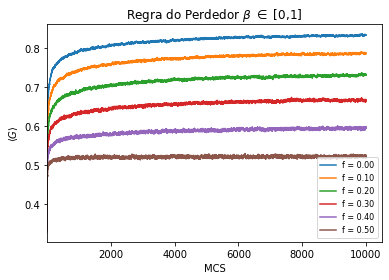
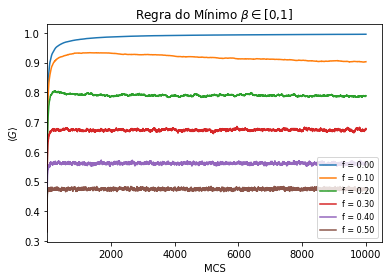
Comparando os dois gráficos é possivel ver que o Índice de Gini apresenta um período transiente antes atingir o regime de equilíbrio. O sistema atinge a o equilíbrio muito rápido quando utilizamos a regra do mínimo, enquanto a regra do perdedor demora mais, assim como é verificado em [1]. Veja que para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = 0 } , o sistema condensa para o caso da regra do mínimo, enquanto que para a regra do perdedor o sistema nunca condensa, estabilizando em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle G \approx 0.8 } (para ser mais exato, em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle G = 0.83 } ) quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = 0 } , coincidindo com os resultados obtidos com a ausência do fator de proteção social nas Figuras 3 e 4.
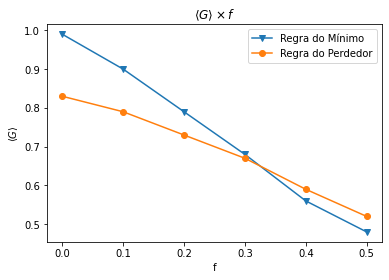
Um dos resultados mais importantes extraídos das Figuras 5 e 6 é ilustrado na Figura 7. Nela vemos um diagrama Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle G \rangle \times f } , onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle G (f) \rangle } é a média sobre cada ensemble do último valor calculado de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle G} para ambas as regras. Nota-se que para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f<0,3} a regra do mínimo possui uma maior desigualdade na distribuição de riqueza, porém quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f> 0,3 } o oposto ocorre, a partir do qual a regra do perdedor começa a gerar uma maior desigualdade na distribuição de riqueza do sistema, apesar da diferença entre os índices de Gini serem menos significantes do que aquelas na região de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f<0,3} .
Esse resultado é amplamente discutido na literatura, e indica que mesmo uma troca justa como a regra do mínimo, que tende sempre a condensação, pode gerar distribuições mais igualitárias que uma troca que naturalmente favorece os agentes mais pobres (regra do perdedor). Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f<0,3 } , a regra do mínimo sempre gera uma distribuição de riqueza mais desigual do que aquelas geradas utilizando a regra do perdedor, porém em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f \approx 0,3} as duas linhas se cruzam, ou seja, as duas regras geram a mesma distribuição de riqueza. A partir de então, para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f>0,3 } , a regra do mínimo começa a gerar distribuições mais igualitárias do que a regra do perdedor. Desta forma, temos que para valores altos de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f } , a regra do mínimo auxilia a ter uma distribuição mais "humanitária", uma vez que já exista políticas sociais suficientes que promovam uma distribuição de renda igualitária. Enquanto isso, a regra do perdedor auxilia a resgatar mais agentes da região de baixa riqueza quando o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f } é muito pequeno [4].
Discussão
Os modelos de distribuição de riqueza por trocas binarias, se mostram muito eficientes para descrever o fenômeno da desigualdade de renda na vida real. As regras do perdedor e do mínimo são propostas muito ricas, mas existem outros modelos conhecidos e passíveis de serem testados. Os resultados que apresentamos aqui são apenas algumas potencialidades que o modelo pode apresentar e condizem com os resultados da literatura consultada. Para aprimoramentos futuros poderia ser interessantes:
- Aumentar o Tempo de simulação para observar as variações no estado transiente do Gini médio, principalmente nos modelos com o fator social;
- Estudar as influências da implementação de diferentes regras de troca entre agentes, que não sejam as regras do mínimo e do perdedor [2];
- Comparar as distribuições de riquezas geradas pela simulação com distribuições reais de renda per capita, por exemplo[5];
- Estudar como perturbações de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} no tempo podem interferir no Gini estacionário do sistema [1];
- Implementar medidas de mobilidade financeira (chamada de liquidez) e correlação de riqueza, que só podem ser calculadas entre MCS [1] [4] [2];
- Testar outras formas mais específicas de auxiliar os agentes mais pobres, que não seja apenas pelo fator de proteção social, como por exemplo taxação uniforme e taxação proporcional à riqueza[5].
Programas
import numpy as np
import matplotlib.pyplot as plt
def Gini(W):
N = len(W)
I = 2 * np.arange(1, N + 1) - N - 1
return np.sum(I * np.sort(W)) / (N * np.sum(W))
Regra do Perdedor sem Fator de Proteção Social
'''parametros'''
N = 10000
n = 1000
GF = 0
e = 10
Gm = np.zeros((e, n))
a_array = np.arange(0, 1, 0.1)
for a in a_array:
for v in range(e):
'''microestado'''
W = np.random.rand(N)
'''macroestado'''
Go = Gini(W)
G = np.zeros(n)
for t in range(n * N):
i = np.random.randint(N)
j = np.random.randint(N)
delta_w = (1-a) * W[j]
W[i] = W[i] + delta_w
W[j] = W[j] - delta_w
if (t % N == 0):
G[t // N] = Gini(W)
T = np.arange(n)
GF = GF + Gini(W)
Gm[v] = G
GM = (GF/e)*np.ones(n)
Gm = np.sum(Gm, axis = 0)/e
plt.plot(T,Gm, label = "$\beta$ = " + str("%.2f" % a) + "")
print("para beta = " + str(a) + " GM = " + str("%.2f" % GM[n-1]) + "")
plt.legend(prop={'size': 8})
plt.xlabel("MCS")
plt.ylabel("$\langle G \rangle$")
plt.ylim(0, 1)
plt.xlim(left = 1)
Gm = np.zeros((e, n))
GF = 0
GM = 0
plt.show()
Regra do Mínimo sem Fator de Proteção Social
'''parametros'''
N = 10000
n = 1000
GF = 0
e = 10
Gm = np.zeros((e, n))
a_array = np.arange(0, 1, 0.1)
for a in a_array:
for v in range(e):
'''microestado'''
W = np.random.rand(N)
'''macroestado'''
Go = Gini(W)
G = np.zeros(n)
for t in range(n * N):
i = np.random.randint(N)
j = np.random.randint(N)
delta_w = (1-a) * min(W[i], W[j])
W[i] = W[i] + delta_w
W[j] = W[j] - delta_w
if (t % N == 0):
G[t // N] = Gini(W)
T = np.arange(n)
GF = GF + Gini(W)
Gm[v] = G
GM = (GF/e)*np.ones(n)
Gm = np.sum(Gm, axis = 0)/e
plt.plot(T,Gm, label = "$\beta$ = " + str("%.2f" % a) + "")
print("para beta = " + str(a) + " GM = " + str("%.2f" % GM[n-1]) + "")
plt.legend(prop={'size': 8})
plt.xlabel("MCS")
plt.ylabel("$\langle G \rangle$")
plt.ylim(0, 1)
plt.xlim(left = 1)
Gm = np.zeros((e, n))
GF = 0
GM = 0
plt.show()
Regra do Perdedor com Fator de Proteção Social
'''parametros'''
N = 10000 # Numero de Agentes
n = 10000 # Numero de MCS
GF = 0
e = 10 # Numero de amostras
a = np.random.rand(N) # Aversão ao risco
Gm = np.zeros((e, n))
f_array = np.arange(0, 0.6, 0.1) # Fatores de proteção social
for f in f_array:
for v in range(e):
'''microestado'''
W = np.random.rand(N) # Riqueza inicial dos agentes
'''macroestado'''
Go = Gini(W)
G = np.zeros(n)
for t in range(n * N):
i = np.random.randint(N)
j = np.random.randint(N)
# Regra do Perdedor com Fator de Proteção Social
p = 0.5+f*((abs(W[i]-W[j]))/(W[i]+W[j]))
aux = np.random.rand()
if aux < p:
if W[j]>W[i]:
delta_w = (1 - a[j]) * W[j]
W[i] = W[i] + delta_w
W[j] = W[j] - delta_w
else:
delta_w = (1 - a[i]) * W[i]
W[i] = W[i] - delta_w
W[j] = W[j] + delta_w
else:
if W[j]<W[i]:
delta_w = (1 - a[j]) * W[j]
W[i] = W[i] + delta_w
W[j] = W[j] - delta_w
else:
delta_w = (1 - a[i]) * W[i]
W[i] = W[i] - delta_w
W[j] = W[j] + delta_w
if (t % N == 0):
G[t // N] = Gini(W)
T = np.arange(n)
GF = GF + Gini(W)
Gm[v] = G
GM = (GF/e)*np.ones(n)
Gm = np.sum(Gm, axis = 0)/e
# Gráficos
plt.plot(T,Gm, label = "f = " + str("%.2f" % f) + "")
print("para f = " + str(f) + " --> GM = " + str("%.2f" % GM[n-1]) + "") # imprime os valores para o gráfico de G x f
plt.legend(prop={'size': 8})
plt.xlabel("MCS")
plt.ylabel("$\\langle G \\rangle$")
plt.xlim(left = 1)
plt.title("Regra do Perdedor $\\beta$ $\\in$ [0,1]")
Gm = np.zeros((e, n))
GF = 0
GM = 0
plt.show()
Regra do Mínimo com Fator de Proteção Social
'''parametros'''
N = 10000 # Numero de Agentes
n = 10000 # Numero de MCS
GF = 1
e = 10 # Numero de amostras
a = np.random.rand(N) # Fatoes de Aversão ao Risco
Gm = np.zeros((e, n))
f_array = np.arange(0, 0.6, 0.1) # Fatores de Proteção Social
for f in f_array:
for v in range(e):
'''microestado'''
W = np.random.rand(N) # Riqueza inicial dos agentes
'''macroestado'''
Go = Gini(W)
G = np.zeros(n)
for t in range(n * N):
i = np.random.randint(N)
j = np.random.randint(N)
# Regra do MÍnimo com Fator de Proteção Social
p = 0.5+f*((abs(W[i]-W[j]))/(W[i]+W[j]))
aux = np.random.rand()
delta_w = min((1 - a[i]) * W[i], (1 - a[j]) * W[j])
if aux < p:
if W[j]>W[i]:
W[i] = W[i] + delta_w
W[j] = W[j] - delta_w
else:
W[i] = W[i] - delta_w
W[j] = W[j] + delta_w
else:
if W[j]<W[i]:
W[i] = W[i] + delta_w
W[j] = W[j] - delta_w
else:
W[i] = W[i] - delta_w
W[j] = W[j] + delta_w
if (t % N == 0):
G[t // N] = Gini(W)
T = np.arange(n)
GF = GF + Gini(W)
Gm[v] = G
GM = (GF/e)*np.ones(n)
Gm = np.sum(Gm, axis = 0)/e
# Gráficos
plt.plot(T,Gm, label = "f = " + str("%.2f" % f) + "")
print("para f = " + str(f) + " --> GM = " + str("%.2f" % GM[n-1]) + "") # imprime os valores para o gráfico de G x f
plt.legend(prop={'size': 8})
plt.xlabel("MCS")
plt.ylabel("$\\langle G \\rangle$")
plt.xlim(left = 1)
plt.title("Regra do Mínimo $\\beta$$\\in$[0,1]")
Gm = np.zeros((e, n))
GF = 0
GM = 0
plt.show()
Referências
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 https://arxiv.org/pdf/1904.05875.pdf CARDOSO, B. F.;GONÇALVEZ, S.; IGLESIAS, J. R.; "WEALTH DISTRIBUTION MODELS WITH REGULATIONS: DYNAMICS AND EQUILIBRIA"
- ↑ 2,0 2,1 2,2 2,3 https://www.lume.ufrgs.br/bitstream/handle/10183/217456/001121445.pdf?sequence=1 CARDOSO, B. F.; "A concentração de riqueza em sistemas de
trocas binárias não enviesadas
" Erro de citação: Etiqueta inválida
<ref>; Nome "MESTRADOBENHUR" definido várias vezes com conteúdo diferente - ↑ https://arxiv.org/pdf/cond-mat/0306579.pdf SCAFETTA, N.;WEST, B. J.; PICOZZI, S.; "A Trade-Investment Model for Distribution of Wealth"
- ↑ 4,0 4,1 4,2 4,3 https://link.springer.com/content/pdf/10.1140/epjst/e2007-00072-4.pdf CAON, G.M.; GONÇALVEZ, S.; CARDOSO, B. F.; "The unfair consequences of equal opportunities: Comparing exchange models of wealth distribution"
- ↑ 5,0 5,1 https://arxiv.org/pdf/2005.06106.pdf IGLESIAS, J. R.; CARDOSO, B. F.;GONÇALVEZ, S.; "Inequality, a scourge of the XXI century"