Equações de Laplace e Poisson
Grupo: Augusto M Giani e Henrique
O objetivo deste trabalho é implementar os métodos de Relaxação, Gauss-Seidel e SOR (Simultaneous OverRelaxation) em problemas de eletroestática, resolvidos pelas equações de Laplace e Poisson. Também temos como objetivo comparar seus resultados: erro entre os métodos e a solução analítica, tempo para estabilização das soluções.
Eletroestática
A Equação de Laplace descreve o Potencial Elétrico () de uma determinada região num espaço que não possui nenhuma densidade de carga elétrica (corpo carregado):
ou na sua versão em 2 dimensões[1]:
Quando neste determinado espaço, delimitado pelas condições de contorno, existe uma densidade de carga, o campo já não se iguala mais à zero, mas sim à densidade de cargas dentro daquela região, sendo descrito agora pela Equação de Poisson:
ou na sua versão em 2 dimensões[1]:
Método de Relaxação
Como podemos ver ambas as equações não dependem do tempo, porém podemos usar um truque para resolver estas equações aplicando o método FTCS (Forward Time Central Space) em uma equação parecida, e fazer a evoluçao temporal durar tempo sufiente para a solução convergir (). Esta operação é chamada de Método de Relaxação.
O que usamos para convergir à solução da Equação de Laplace foi uma equação de difusão genérica:
Fazendo , para a equação de difusão temos a intuição que dada condição inicial estacionária, a solução não diverge e "relaxa" para uma função que não depende mais do tempo:
Com isso: , e chegando assim à Equação de Laplace e possibilitando chegar na discretização da Equação de Poisson. Então basicamente utiliza-se da mesma discretização de uma equação de difusão, porém a evolução temporal só serve para convergirmos à solução da Equação de Laplace com as condições iniciais que propomos. Os métodos de Jacobi, Gauss-Seidel e SOR são considerados Métodos de Relaxação[2].
Métodos Numéricos
Foram implementadas as seguintes discretizações para os problemas de eletroestática.
Método de Jacobi
Equação de Laplace
Para equação de Laplace partimos de:
Discretizando, primeiro chegamos que:
Seguindo mesmo procedimento do método de FTCS, temos a mesma condição de estabilidade:
No nosso algoritmo ultizamos então obtivemos a condição de estabilidade:
Para o algoritmo de Jacobi (Relaxação) escolhemos o valor de e com isso resulta na equação final:
onde n representa o passo no tempo, i representa o passo em X e j representa o passo em Y. A constante somente representava uma similaridade com a equação de difusão para demonstrar que este valor não interfere na equação final, ele sequer aparece (portanto podemos desconsiderá-lo, como faremos na equação de Poisson).
Equação de Poisson
Partindo de:
chegamos em:
Para nosso problema , então multiplicando os dois lados por , chegamos em:
E finalmente, aplicando a condição de estabilidade e cancelando os termos :
Método de Gauss-Seidel
O Método de Gauss-Seidel adianta (no tempo) a chegada da solução estacionária, utilizando termos que já foram calculados num passo anterior de tempo para calcular o ponto atual. Isto é, ao fazer a iteração, para calcular o valor de algum ponto são utilizados dois valores que já foram atualizados na mesma iteração e dois que foram calculados na iteração passada. Com isso é de se esperar que há uma variação mais rápida dos valroes do plano, quando comparado com o método anterior.
Equação de Laplace
Para equação de Laplace, obetemos a seguinte equação de iteração:
Equação de Poisson
Como pode-se notar, o termo que distingue a Equação de Laplace para a Equação de Poisson é apenas o termo que soma ao lado direito da equação. Assim temos a seguinte equação de iteração:
Método SOR (Simultaneous Overrelaxation)
Como pode-se notar nas equações (é mais intuitivo na forma discretizada da Equação de Laplace), a atualização de um ponto é feita através de uma espécie de "média" dos pontos, no tempo anterior, ao seu arredor (o ponto acima, à direita, à esquerda e abaixo na matriz dos ). O método introduz nesse cálculo de "média" (ainda no método de Gauss-Seidel), pesos para a contribuição dos pontos da vizinhança e também um peso para o próprio ponto no tempo anterior.
Equação de Laplace
Aplicando os pesos na forma discretizada da equação de Laplace pelo método de Gauss-Seidel:
Equação de Poisson
Da mesma forma aplicamos os pesos na forma discretizada da equação de Poisson pelo método de Gauss-Seidel:
Todas as equações em Azul descritas acima foram implementadas em nossos códigos.
Problemas propostos
Problema da borda carregada
Equação de Laplace aplicada a um plano com uma das quatro "bordas" carregada. Consideramos as dimensões de e como (um plano quadrado) para facilitar os cálculos.
Condições iniciais e de contorno:
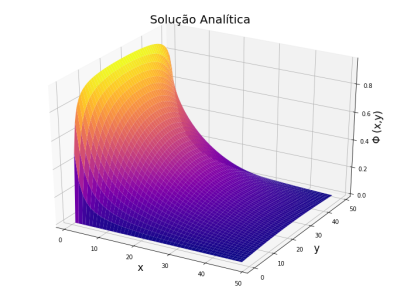
Para a solução analítica do problema temos que:
Problema do Dipolo Elétrico
Equação de Poisson considerando uma dipolo elétrico como densidade de carga :
Utilizamos como condições iniciais e de contorno do problema:
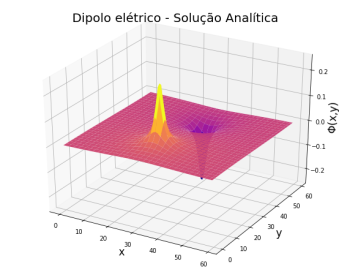
Temos a solução do potencial eletroestático de cada partícula no plano dada por:
Onde consideramos as constantes com sendo = 1 para facilitar a modelagem do problema.
Implementação
Implementamos as simulações em Python3, no ambiente Colab da Google. Junto com as soluções numéricas também implementamos a solução analítica de um problema para compararmos com a solução numérica
Os códigos se encontram no final desta Wiki, mas uma observação geral é que além de utilizarmos as equações destacadas em Azul para implementar as soluções, é importante lembrar que o resultado final só é atingido quando iteramos as soluções no "tempo", então é preciso iterar os elementos da matriz no espaço, mas também fazer ela evoluir com o tempo, exemplo para o algoritmo de Jacobi, Equação de Laplace:
### Exemplo da evolução temporal no método de relaxação ###
# P é a matriz do potencial no tempo n
# Q é a matriz do potencial no tempo n+1
while t < tmax: # Loop temporal
for i in range(1,L+1): # Loop em x
for j in range(1,L+1): # Loop em y
Q[i][j] = (P[i+1][j] + P[i-1][j] + P[i][j+1] + P[i][j-1])/4
P = Q.copy()
t = t + td
plt.plot(x,y,P)
Lembrando que estamos resolvendo o problema em 2D, por isso P e Q são matrizes, onde cada elemento representa um ponto no plano. Como pode-se ver, somente é plotado um gráfico, ou somente se é considerado como resultado final o estado final do vetor P, depois que ele sai do loop while. Esta lógica foi usada para todos os métodos que aplicamos[3] [4].
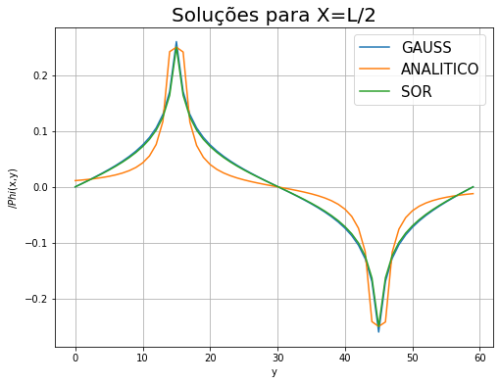
Resultados do problema da Borda Carregada
Apresentamos as seguintes soluções do problema com a Equação de Laplace pois já é um problema bem documentado com resultados mais palpáveis para compararmos e analisarmos a implementação dos métodos.
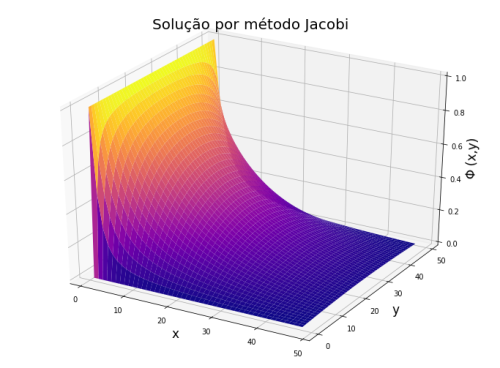
Método de Jacobi
Obtivemos a seguinte solução pelo método explícito:
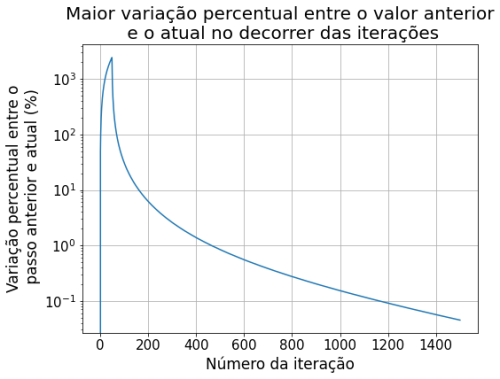
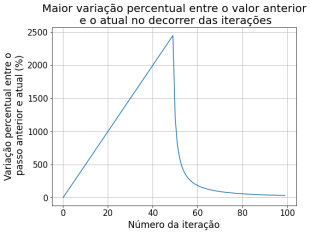
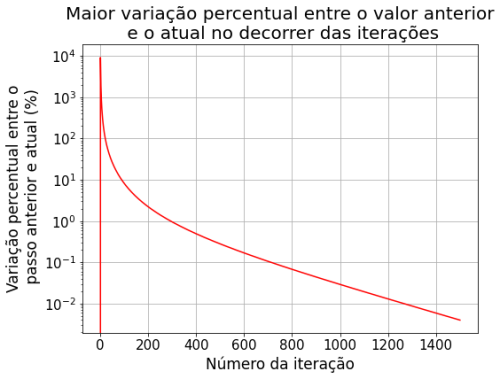
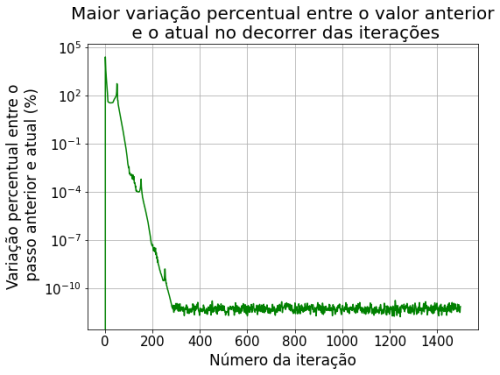
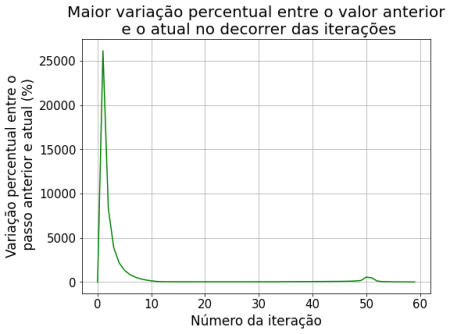
Comparando com a iteração no passo de tempo anterior, obtivemos as seguintes diferenças entre o passo n+1 e o passo n:
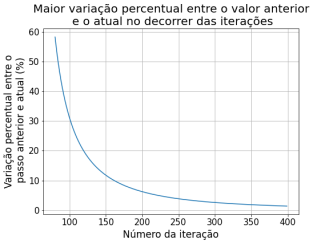
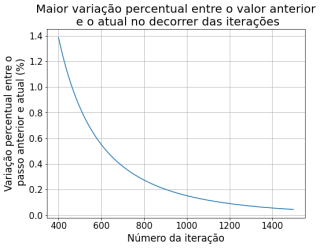
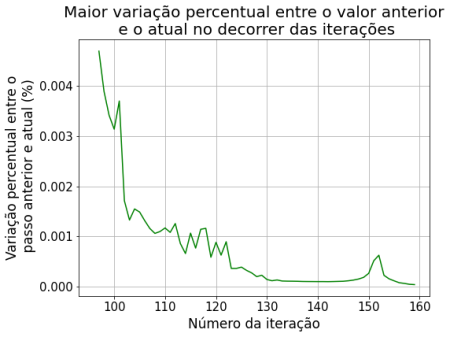
Dando mais zoom nas iterações futuras podemos ver que as variações (%) se tornam menores, indicando que o método converge para a solução estacionária.
O maior erro aqui considerado no gráfico é do ponto do plano de 50x50 do nosso problema que apresentou maior diferença de valor em relação à iteração temporal anterior. Utilizamos o mesmo padrão de resultado de erro nos outros métodos.
Método de Gauss-Seidel
Obtivemos a seguinte solução pelo método de Gauss-Seidel:
Comparando com a iteração no passo de tempo anterior, obtivemos as seguintes diferenças entre o passo n+1 e o passo n:
Aplicamos zoom nas iterações futuras, onde podemos ver que as variações (%) se tornam tão pequenas que praticamente o método converge para a solução estacionária. Iremos discutir posteriormente que esta solução converge, com erro bem menor, antes do que o método de Jacobi
Método SOR (Simultaneous Overrelaxation)
Obtivemos a seguinte solução aprimorando o método de Gauss-Seidel para Simultaneous OverRelaxation:
Comparando com a iteração no passo anterior, podemos fazer a seguinte análise:
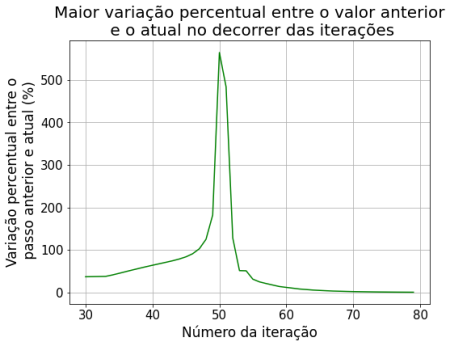
Aplicando zoom nas iterações futuras, onde podemos notar um comportamento anômalo no "erro" em iterações múltiplas de 50 (tamanho da grade).
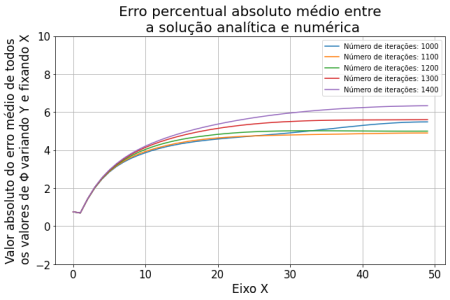
Resultados do problema do Dipolo Elétrico
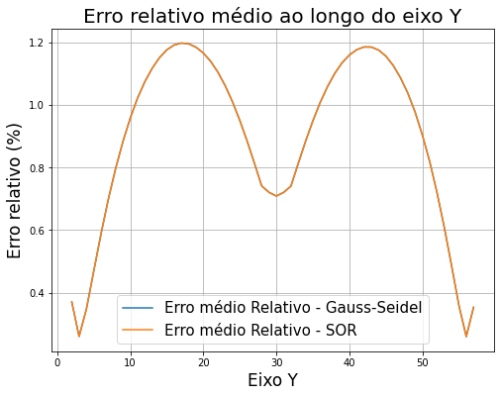
Para o Problema do Dipolo Elétrico (através da Equação de Poisson) compararmos e analisarmos a implementação dos métodos focando no erro proporcionado pelos métodos numéricos.
Método de Gauss-Seidel
A implementação foi realizada conforme descrito na seção de Métodos Numéricos.
Método de SOR
Assim como a implementação do método de Gauss-Seidel, obtivemos os seguintes resultados com o método de SOR.
Discussão
Resultados do Método de Jacobi
Primeiro começamos pelo Método de Jacobi, também conhecido por FTCS, modelando um problema conhecido para compararmos a precisão de nossos algoritmos com a solução analítica. Ao resolver o potencial elétrico nas condições do problema da borda carregada obtivemos o comportamento da curva igual ao esperado analiticamente.
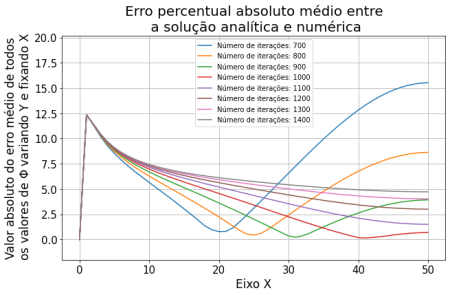
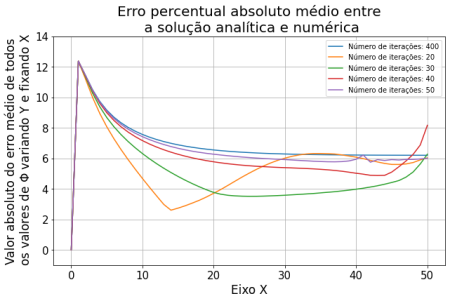
Sobre o método de relaxação observa-se que nas primeiras iterações há uma variação muito grande dos valores da solução. Nas primeiras 60 iterações, os valores do potencial variaram em até 2500% em relação ao passo anterior. Percebe-se que a partir de 160 iterações começa a ter uma variação menor que 10%, e a partir de 1200 passos já atingimos uma variação menor que 0.1%. Por esse método convergir mais devagar, assumimos os 1500 passos pois sabíamos que os outros métodos iriam convergir com menos iterações. Decidimos comparar os métodos com 1500 passos, a partir disso já não notamos mais variação significativa.
Problema da Borda Carregada
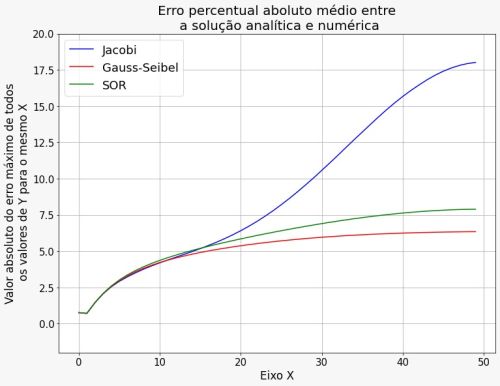
Pela teoria dos métodos de relaxação, sabemos que a precisão do método de Superrelaxação é para ser maior que a precisão
Importante ressaltar que este método além de convergir mais rápido para uma solução, ele apresenta menos erro com menos iterações do que o método de Gauss-Seidel, isso se deve ao fato que ele leva em consideração o seu mesmo ponto no passo anterior para atualizá-lo no próximo passo, deixando o método mais preciso.
Importante ressaltar que para o método de Gauss uma quantidade menor de iterações no tempo, obtivemos erros menores, comparando com o método explícito, o que mostra uma eficácia maior do método.
UMA COISA QUE EU QUERO FALAR É SOBRE A FACILIDADE DE MODELAR UM PROBLEMA COMPLEXO DE ELETROESTÁTICA SEM TER QUE RESOLVER CONTAS, APENAS APLICAR A EQUACAO DIFERENCIAL E DEU ENTENDEU? si pá vey se pá vei si pa
Problema do Dipolo Elétrico
Referências
- ↑ 1,0 1,1 GRIFFITHS, David J. Introduction to electrodynamics. New Jersey: Prentice Hall, 1962.
- ↑ GARCIA, Alejandro L. Numerical methods for physics. Englewood Cliffs, NJ: Prentice Hall, 2000.
- ↑ Numerical solution of partial differential equations, Dr. Louise Olsen-Kettle. The University of Queensland School of Earth Sciences Centre for Geoscience Computing.
- ↑ SAYAMA, Hiroki. Introduction to the modeling and analysis of complex systems. Open SUNY Textbooks, 2015.