Integração Numérica
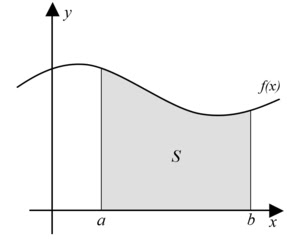
Integração numérica é um termo amplo que abrange até a integração de equações diferenciais como é discutido em Métodos Computacionais B. Aqui nos referimos exclusivamente ao cálculo numérico da integral definida:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S = \int_{a}^{b} f(x) dx}
O termo definida, quer dizer que a integral se faz entre limites definidos, no caso a e b.
O interesse de fazer esse cálculo numericamente se deve a:
- existência de funções contínuas sem primitiva, o que inviabiliza a conta analítica.
- funções descontinuas ou definidas por trechos
- funções (ou tabelas) provenientes de experimentos
- funções continuas e com primitiva de representação simbólica, porem de difícil avaliação na prática (mais difícil que avaliar a própria função)
Definição
Revisemos o conceito de integral do cálculo: A integral definida de uma função f(x) no intervalo [a, b] se define como:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S = \int_a^b f(x)\, dx = \lim_{N\to\infty} \sum_{i=0}^{N} f(x_i) \Delta x }
A integral de f(x) pode ser entendida como a soma de pequenos retângulos de base dx e altura f(x), onde o produto f(x) dx é a área deste retângulo.
A soma de todas estas pequenas áreas, ou áreas infinitesimais, fornece a área total abaixo da curva.
Mais precisamente podemos dizer que a integral acima é o valor limite da soma:
onde:
é o comprimento dos pequenos intervalos nos quais dividimos o intervalo (b-a),
é o valor da função em algum ponto deste intervalo.
Quando o valor da soma acima é igual a área abaixo da curva.
A integral também é conhecida como antiderivada:
Relembremos porque:
Teorema Fundamental do Cálculo
Se resolvermos a integral acima entre os limites a e b, o resultado pode ser escrito como dependendo só dos extremos:
Vamos ver agora como se isso for válido, então F(x) é a primitiva procurada.
Calculando a integral entre e :
Pela definição da integral entre limites definidos podemos escrevê-la como:
onde é um valor de entre os extremos do intervalo.
Passando o para a direita e tomando o limite quando ele vai para zero:
Demonstramos que a derivada de F(x) resulta ser a função f(x) que queremos integrar. Em outras palavras, o Teorema fundamental do Cálculo diz que resolver uma integral se resume a achar a primitiva, ou seja uma função cuja derivada seja o integrando.
O problema prático é que não todas as funções tem primitiva.. Vejamos então.
Cálculo Numérico
O cálculo numérico de uma integral definida se baseia na própria definição acima.
Com a diferença que N é finito. Obviamente quanto maior, melhor.
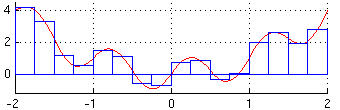
-Temos que pelos retângulos definidos pelo extremo esquerdo de cada subintervalo:
-E pelos retângulos definidos pelo extremo direito de cada subintervalo:
Regra do Trapézio:
onde:
Esta última pode ser reescrita como:
Também pode se verificar que a integral calculada com os trapézios é a média das integrais calculadas com retângulos:
Regra de Simpson:
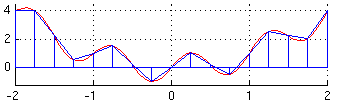
Notemos que o método do trapézio é baseado na ideia de passar uma reta por 2 pontos e aproximar a área da função f(x) pela área sob a curva definida pelo trapézio.
A regra de Simpson é uma extensão disto: a ideia é passar uma parábola por três pontos consecutivos e calcular a área definida por ela. Se tivermos apenas 3 pontos, a integral da parábola que passa entre é dada por:
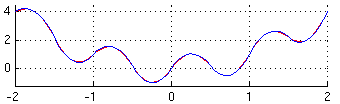
No entanto, para integrarmos sobre toda o intervalo com boa precisão, é necessário dividi-lo em N intervalos, com N grande (e par!). Assim, é preciso traçar uma parábola a cada três pontos consecutivo e a expressão final da fórmula de Simpson é então a soma da área sob todas as parábolas do intervalo :
- ,
onde .
A dedução da regra de Simpson pode ser encontrada por exemplo em [1].
Programação
A seguir um trecho do programa para cálculo da integral da função f(x) (external function f(x))
entre a e b com N pontos, usando o método dos retângulos pela esquerda:
... Read*, a, b, N dx = (b-a)/N; S=0 Do i = 0, N-1 x = a + i*dx S = S + f(x) EndDo Print*, "Integral S=", S*dx ...
Os outros métodos se programam de maneira similar mudando limites (índice do laço)
e/ou tratando de forma diferente os valores das pontas.
Erro associado ao método numérico
O método de integração numérico não retorna o valor exato de uma função, visto que não podemos ter no computador . O erro aqui discutido estará vinculado ao número de divisões realizada na função dentro do intervalo que se quer saber o valor da integral. Assim, o erro é definido como
- ,
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Int(N)} é o valor retornado pelo método numérico utilizado utilizando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} divisões e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle Int(N-1)} utilizando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N-1} divisões. Note que um teste simples para verificar quando a resposta está convergindo é aumentar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} e calcular o erro a cada incremento no seu valor.




















![{\displaystyle S=\int _{x_{0}}^{x_{2}}f(x)\,dx\approx {\frac {x_{2}-x_{0}}{6}}\left[f(x_{0})+4f\left({\frac {x_{0}+x_{2}}{2}}\right)+f(x_{2})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d31dbd09bee9d8b68ae351b3404a51af97b7da72)
![{\displaystyle \left[x_{1};x_{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51ccf1403a3a8371e93df66a55a13a79617a6488)
![{\displaystyle \left[x_{0};x_{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6f8b10d35dbd8481b6bd4f2501c28ef78eddee3)
![{\displaystyle S=\int _{x_{0}}^{x_{n}}f(x)dx\simeq {\frac {h}{3}}\left[f(x_{0})+4f(x_{1})+2f(x_{2})+4f(x_{3})+\ldots +4f(x_{n-1})+f(x_{n})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed00f4a5437e94106887dedbabfe2ad2b539392d)



