Modelo de Ising

Autores: André Guimarães, Filssen Schereiber, João Roth e Lucas Oliveira

Este trabalho tem como objetivo estudar o Modelo de Ising...

Introdução

O modelo de Ising surgiu na década de 1920 como uma simplificação do modelo de Heisenberg. Inicialmente desenvolvido para compreender o ferromagnetismo, passou, ao longo dos tempo, a ser aplicado em diversas áreas interdisciplinares, tais como biologia, neurociência, dinâmica social e economia, devido a sua simplicidade.

Este é, provavelmente, o modelo mais comumente estudado na mecânica estatística. É possível dizer que o modelo de Ising é, para a mecânica estatística, o que a mosca-da-fruta é para a genética. O modelo possibilita ilustrar o conceito essencial de como o equilíbrio entre energia e entropia conduz a uma mudança de fase. (falta a referência)

Foram realizados diversos estudos sobre matemática, física e as potenciais aplicações desse modelo. Neste trabalho, pretendemos explorar alguns aspectos fundamentais e os resultados possíveis de serem obtidos por meio de simulações de Monte Carlo em sistemas magnéticos com diversas dimensionalidades.

Problema com o modelo de Heisenberg

Em 1924, Wilhelm Lenz delegou a seu aluno de graduação Ernst Ising a tarefa de compreender e resolver o modelo de Heisenberg para o ferromagnetismo. Heisenberg propõe um modelo de rede que busca explicar o ferromagnetismo em sólidos a partir da energia de interação entre os spins. Por exemplo, podemos considerar uma rede quadrada com contornos periódicos onde os elétrons do sólido são distribuídos uniformemente. Dessa forma, podemos descrever a energia resultante da interação entre quaisquer dois elétrons como:

$E_{ij}=-J_{ij}({\vec {S}}_{i}\cdot {\vec {S}}_{j})$

(1)

Na equação acima, $J_{ij}$ representa uma constante de troca que denota a intensidade da interação $J$ entre dois spins vizinhos. Caso os spins não sejam vizinhos, esse coeficiente de interação é nulo. Além disso, os vetores ${\vec {S}}_{i}$ e ${\vec {S}}_{j}$ representam os momentos magnéticos. Portanto, através do produto escalar, a energia depende da projeção de um momento magnético em relação ao outro: será $+1$ se estiverem alinhados e $-1$ se estiverem em sentidos contrários.

Vale ressaltar que o coeficiente J é positivo, o que implica em contribuições negativas na energia quando os vetores momento magnético são paralelos, devido ao sinal negativo da expressão. Por conseguinte, para spins antiparalelos, observa-se um aumento na energia. Como esperado, o sistema tende a permanecer no estado de menor energia. Assim, os spins do sistema tendem a se alinhar, como é característico de uma fase ferromagnética.

Esse sistema tem um Hamiltoniano da forma:

${\mathcal {H}}=-J\sum _{\langle ij\rangle }({\vec {S}}_{i}\cdot {\vec {S}}_{j})$

(2)

Na expressão, os símbolos de bra-ket são usados para representar a soma sobre os primeiros vizinhos. Contudo, desse sistema, temos uma função de partição da forma:

${\mathcal {Z}}=\sum _{E_{i}}e^{\frac {E_{i}}{K_{B}T}}$

(3)

Essa expressão representa o somatório de todas as configurações da exponencial da energia de cada configuração dividida pela constante de Boltzmann e pela temperatura.

Nesse momento, Ising se deparou com um problema, pois, além de possuir poucos recursos matemáticos na época, o número de configurações é infinito, uma vez que é possível observar qualquer direção entre os vetores momento magnético de forma contínua.

Modelo de Ising

Ising resolveu o problema das infinitas configurações assumindo que, ao invés de lidar com spins que rotacionam 360 graus nas três coordenadas espaciais, ele selecionaria uma coordenada e consideraria a projeção dos spins nela. Na prática, ele conseguiu reduzir o problema de infinitas configurações para apenas duas: ou o spin aponta para o sentido positivo do eixo, ou para o sentido negativo.

Dessa forma, o uso do produto escalar para os vetores de momento magnético não é mais necessário, uma vez que esses agora assumem valores entre $-1$ e $+1$. Assim, podemos escrever o Hamiltoniano como:

${\mathcal {H}}=-J\sum _{\langle ij\rangle }S_{i}S_{j}$

(4)

Com essas considerações, torna-se possível descrever a transição de fase entre ferromagnetismo e paramagnetismo em sistemas ao menos bidimensionais.

Além disso, podemos introduzir um termo no Hamiltoniano responsável por descrever o sistema na presença de um campo magnético externo:

${\mathcal {H}}=-J\sum _{\langle ij\rangle }S_{i}S_{j}-H\sum _{i}S_{i}$

(5)

onde H é um coeficiente relacionado ao campo magnético externo. O acréscimo desse termo faz com que o estado de menor energia seja aquele favorável à direção desse campo.

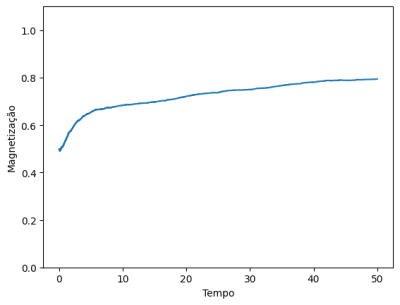
Para o estudo da transição de fase magnética definimos uma grandeza chamada de magnetização. Essa grandeza é responsável para computar a média de todos os spins do sistema e, nesse caso, será o parâmetro de ordem. Seja $N$ o número de spins do sistema, escrevemos a magnetização como:

$M={\frac {1}{N}}\sum _{i}S_{i}$

(6)

ou ainda, é possível expressarmos a magnetização em função do número de spins para cima $N_{\uparrow }$ ou para baixo $N_{\downarrow }$:

$M={\frac {N_{\uparrow }-N_{\downarrow }}{N}}$

(7)

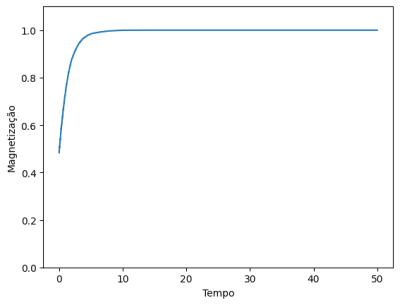
Com essa notação, é possível observar um comportamento característico da magnetização. A magnetização será próxima de zero quando os números de spins para cima e para baixo forem próximos, ou seja, quando o sistema está em um estado de alta desordem. Por outro lado, para valores do módulo da magnetização próximos da unidade, temos um sistema bem ordenado, com praticamente todos os spins paralelos entre si.

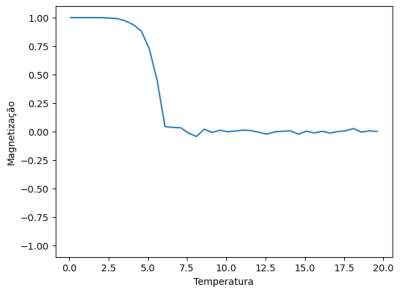
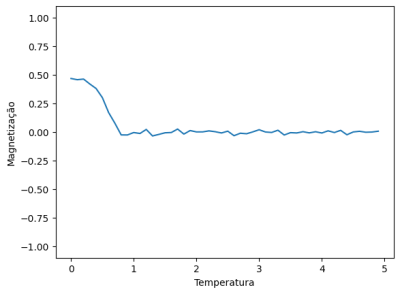
Esse comportamento, conforme esperado do parâmetro de ordem, auxilia na distinção clara da transição de fase de um estado ordenado para um estado desordenado. Tal visualização pode ser realizada fixando alguns parâmetros físicos do sistema e analisando o comportamento da magnetização em relação à temperatura ou ao campo externo, por exemplo.

Implementação (protótipo)

Algoritmo de Metrópolis

O algoritmo de Metrópolis em Monte Carlo é uma técnica fundamental em simulações computacionais, amplamente utilizada em física estatística, química computacional, ciência dos materiais e várias outras áreas. Ele é utilizado para amostragem de configurações de um sistema físico ou químico de acordo com a sua distribuição de probabilidade, mesmo quando essa distribuição é desconhecida ou difícil de calcular diretamente.

Algoritmo de Metrópolis para o modelo de Ising:

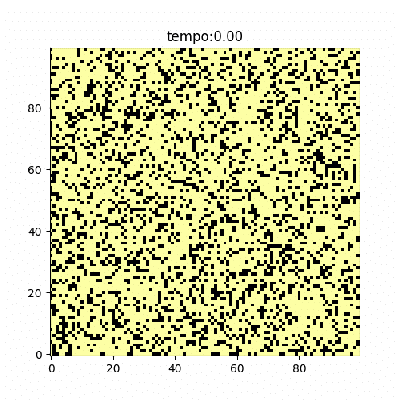
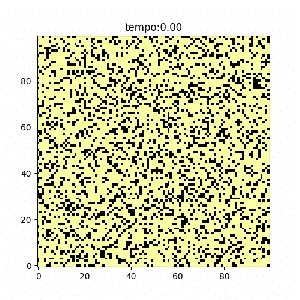
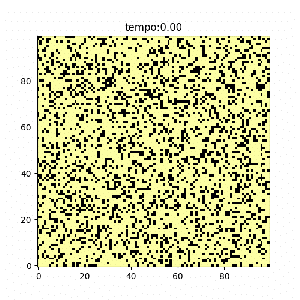
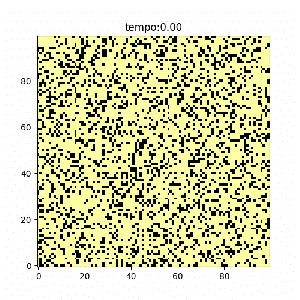
• 1) Inicialização: Começamos com uma configuração inicial do sistema. Nesse caso, iniciamos uma rede de spins aleatoriamente desemparelhados;

• 2) Proposição de uma Mudança: Uma nova configuração do sistema é proposta. Isso pode ser feito mudando a configuração de um spin aleatório da rede;

• 3) Avaliação da Aceitação da Mudança: Avaliamos a probabilidade de aceitar a nova configuração proposta. Se a nova configuração for mais provável do que a configuração atual, ela será aceita automaticamente. Caso contrário, a aceitação será baseada em uma probabilidade determinada pela relação entre as probabilidades das duas configurações, de acordo com a condição de balanceamento detalhado:

${\frac {A(a\rightarrow b)}{A(b\rightarrow a)}}=e^{-{\frac {E_{b}-E_{a}}{k_{B}T}}}=e^{-{\frac {\Delta E}{k_{B}T}}}$

(8)

• 4) Atualização do Sistema: Se a mudança for aceita, o sistema é atualizado com a nova configuração. Caso contrário, o sistema permanece no estado atual.

• 5) Repetição: Repetimos os passos 2-4 por um grande número de iterações ou até que o sistema atinja o equilíbrio termodinâmico.

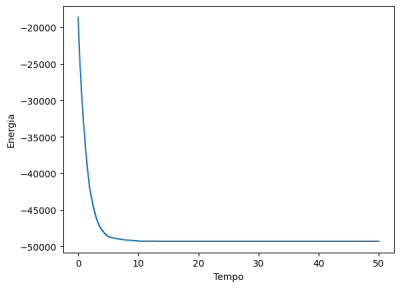
O aspecto crucial do algoritmo de Metrópolis é a garantia de que, à medida que o número de iterações tende ao infinito, a distribuição de configurações amostradas converge para a distribuição de equilíbrio do sistema.

É válido notar que, em nossa primeira análise, avaliamos as energias de cada estado conforme a equação (4), na qual há interação apenas entre primeiros vizinhos.

Algoritmo de Metropolis para segundos vizinhos

Com o objetivo de implementar interações de segundos vizinhos ao modelo de Ising é necessário modificá-lo levemente, transformando a equação (5) na seguinte equação:

${\mathcal {H}}=-J_{1}\sum _{\langle ij\rangle }({\vec {S}}_{i}\cdot {\vec {S}}_{j})-J_{2}\sum _{\langle ik\rangle }({\vec {S}}_{i}\cdot {\vec {S}}_{k})-H\sum _{i}S_{i}$

(10)

Onde o índice j indica os primeiros vizinhos do índice i, enquanto os índices k indicam os segundos vizinhos do mesmo. A partir dessa simples alteração é possível gerar comportamentos distintos, de acordo com a relação entre os parâmetros $J_{1}$ e $J_{2}$.

O algoritmo de Metropolis garante que o modelo de Ising leve em conta a temperatura mas ainda tenda ao seu estado de menor energia. Para tal um spin aleatório da malha sofre um "flip", ou seja, seu valor é multiplicado por $-1$. Com essa modificação na malha, a energia é calculada e comparada à energia antes da modificação. Caso a variação seja negativa a alteração é aceita; mas se for positiva só será aceita com uma probabilidade de $e^{-\beta \Delta E}$. Isso garante que altas temperaturas permitam mais alterações positivas, gerando mais ruído.

No entanto, a fim de simplificar computacionalmente a conta, o $\Delta E$ é calculado diretamente utilizando a seguinte equação:

$\Delta E=2J_{1}{\vec {S}}_{i}\sum _{j}{\vec {S}}_{j}+2J_{2}{\vec {S}}_{i}\sum _{k}{\vec {S}}_{k}+2HS_{i}$

(11)

Sendo i o índice do spin sorteado a ser invertido. Nota-se que é possível determinar o próximo passo para o sistema sem mesmo calcular sua energia ou modificá-lo, basta utilizar a equação (11) e os critérios do algoritmo de Metropolis.

Resultados

Malha Bidimensional

Interações de Segundos Vizinhos

Diversos casos foram estudados a fim de encontrar semelhanças e diferenças em seus comportamentos. O primeiro caso estudado apresenta correlação exata entre $J_{1}$ e $J_{2}$, ou seja, ambos iguais a 1. O segundo caso apresenta uma interação fraca e contrária para segundos vizinhos, ou seja $J_{1}=1$ e $J_{2}=-0.1$. O terceiro caso demonstra uma interação mais forte (mas ainda contrária) para segundos vizinhos, ou seja, $J_{1}=1$ e $J_{2}=-0.3$. Por fim o quarto caso exemplifica uma situação instável, onde $J_{1}=-1$ e $J_{2}=-1$. Todos os casos partem da mesma condição inicial, onde 75% da malha se encontra com spin positivo e 25% com spin negativo.

Primeiro Caso

Evolução temporal para $J_{1}=1$, $J_{2}=1$, $H=0$ e $T=0.1$.	Evolução temporal da magnetização para $J_{1}=1$, $J_{2}=1$, $H=0$ e $T=0.1$
Relação entre temperatura e magnetização de equilíbrio para $J_{1}=1$, $J_{2}=1$ e $H=0$	Evolução temporal da energia para $J_{1}=1$, $J_{2}=1$, $H=0$ e $T=0.1$

---

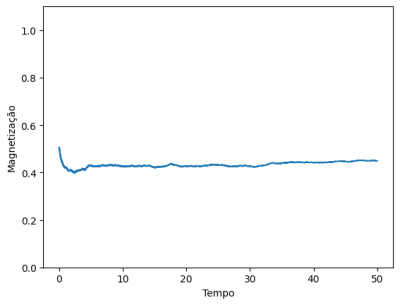
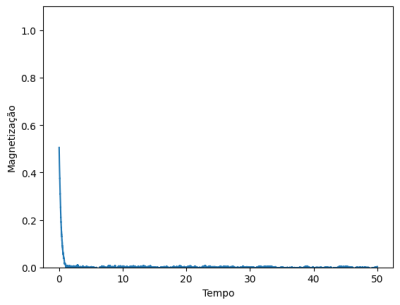
O primeiro caso apresenta as mesmas características que o modelo de primeiros vizinhos, sua única diferença está na intensidade da correlação local que é aumentada significativamente. Isso faz com que a malha atinja o equilíbrio de forma mais rápida, mas também faz com que a temperatura necessária para uma troca de fase aumente drasticamente.

É importante relembrar pela equação (8) que o número de segundos vizinhos é bem maior do que primeiros vizinhos, o que faz com que $J_{2}$ tenha um papel muito mais importante na dinâmica do sistema do que $J_{1}$.

Segundo Caso

Evolução temporal para $J_{1}=1$, $J_{2}=-0.1$, $H=0$ e $T=0.1$.

O segundo caso apresenta características bem distintas do modelo de primeiros vizinhos, mas a principal é que seu estado de equilíbrio depende muito da temperatura escolhida. O modelo de primeiros vizinhos apresenta uma troca de fase para altas temperaturas, onde o sistema é tomado por ruídos que tornam a malha paramagnética. Aqui isso também ocorre, mas existe uma segunda troca de fase para temperaturas muito baixas. Isso ocorre pois a falta de ruído permite que a fraca interação de segundos vizinhos se manifeste, criando falhas na malha que não permitem a malha se alinhar completamente. Já em temperaturas intermediárias, o ruído gerado é capaz de desfazer as falhas da malha, permitindo que ela atinja um alinhamento completo. Outra alteração importante pode ser vista na transição de fase para altas temperaturas: a temperatura crítica diminuiu ligeiramente.

Evolução temporal da energia para $J_{1}=1$, $J_{2}=-0.1$, $H=0$ e $T=0.1$

Evolução temporal da magnetização para $J_{1}=1$, $J_{2}=-0.1$, $H=0$ e $T=0.1$

Relação entre temperatura e magnetização de equilíbrio para $J_{1}=1$, $J_{2}=-0.1$ e $H=0$

Terceiro Caso

Evolução temporal para $J_{1}=1$, $J_{2}=-0.3$, $H=0$ e $T=0.1$.

O segundo caso apresenta características próximas do segundo, mas sua maior intensidade para interações de segundos vizinhos lhe dá características únicas. A principal característica se apresenta em baixas temperaturas que não mais possuem fase ferromagnética, as falhas na malha são muito numerosas e impedem seu alinhamento. No entanto é possível notar que ainda existe uma transição de fases, mesmo que em temperaturas muito mais baixas. Essa transição ocorre entre dois estados paramagnéticos, um causado por falhas naturais e estáveis da malha, e outro causado por ruído aleatório e inconstante gerado pela temperatura.

Evolução temporal da energia para $J_{1}=1$, $J_{2}=-0.1$, $H=0$ e $T=0.1$

Evolução temporal da magnetização para $J_{1}=1$, $J_{2}=-0.1$, $H=0$ e $T=0.1$

Relação entre temperatura e magnetização de equilíbrio para $J_{1}=1$, $J_{2}=-0.1$ e $H=0$

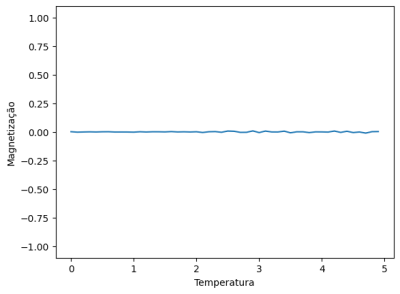
Quarto Caso

Evolução temporal para $J_{1}=-1$, $J_{2}=-1$, $H=0$ e $T=0.1$.

Este caso demonstra um material com baixa interação magnética com campos externos, um material que naturalmente procura estados de magnetização nula. No entanto, a interação negativa de segundos vizinhos impossibilita que a malha atinja uma estado estático, pois vários estados de equilíbrio são apresentados para uma mesma energia. É importante ressaltar que o estado não possui mais uma mudança de fase já que naturalmente apresenta magnetização próxima de zero; mas o aumento de temperatura aumenta em muito seu ruído, alterando sua energia de equilíbrio.

Evolução temporal da energia para $J_{1}=1$, $J_{2}=-0.1$, $H=0$ e $T=0.1$

Evolução temporal da magnetização para $J_{1}=1$, $J_{2}=-0.1$, $H=0$ e $T=0.1$

Relação entre temperatura e magnetização de equilíbrio para $J_{1}=1$, $J_{2}=-0.1$ e $H=0$