Derivada Numérica: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 98: | Linha 98: | ||
Primeiramente, a figura 1 mostra a derivada à direita, onde a curva em vermelho representa <math>f(x)</math> e a curva em azul representa a derivada de <math>f(x)</math>. | Primeiramente, a figura 1 mostra a derivada à direita, onde a curva em vermelho representa <math>f(x)</math> e a curva em azul representa a derivada de <math>f(x)</math>. | ||
[[Imagem:derivada3.png|thumb|300px|left|Figura 1]] | [[Imagem:derivada3.png|thumb|300px|left|Figura 1 - Derivada à direita]] | ||
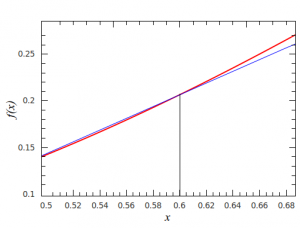
A figura 2 mostra um zoom no ponto <math>x</math> com a curva da derivada calculada pelo método descrito acima. Em azul a derivada calculada numericamente, só que agora com um deslocamento em <math>y</math> para passar pelo ponto <math>(f(x),x)</math>. | A figura 2 mostra um zoom no ponto <math>x</math> com a curva da derivada calculada pelo método descrito acima. Em azul a derivada calculada numericamente, só que agora com um deslocamento em <math>y</math> para passar pelo ponto <math>(f(x),x)</math>. | ||
[[Imagem:derivada4.png|thumb|300px|Figura 2]] | [[Imagem:derivada4.png|thumb|300px|Figura 2 - Derivada à direita (zoom)]] | ||
O exemplo do método de derivada centrada está representado na figura 3. Em vermelho a curva <math>f(x)</math> e em azul a sua derivada. | O exemplo do método de derivada centrada está representado na figura 3. Em vermelho a curva <math>f(x)</math> e em azul a sua derivada. | ||
[[Imagem:derivada1.png|thumb|300px|left|Figura 3]] | [[Imagem:derivada1.png|thumb|300px|left|Figura 3 - Derivada centrada]] | ||
A figura 4 mostra um zoom com a curva da derivada centrada em <math>x</math>. | A figura 4 mostra um zoom com a curva da derivada centrada em <math>x</math>. | ||
[[Imagem:derivada2.png|thumb|300px|Figura 4]] | [[Imagem:derivada2.png|thumb|300px|Figura 4 - Derivada centrada (zoom)]] | ||
Além da ilustração dos métodos de derivação numérica, as figuras 5 e 6 mostram o gráfico do valor retornado pelo método da derivação à direita em função do incremento <math>\Delta x</math> utilizado. | Além da ilustração dos métodos de derivação numérica, as figuras 5 e 6 mostram o gráfico do valor retornado pelo método da derivação à direita em função do incremento <math>\Delta x</math> utilizado. | ||
[[Imagem:der.png|thumb|300px|left|Figura 5]] | [[Imagem:der.png|thumb|300px|left|Figura 5 - Erros de truncamento e precisão]] | ||
[[Imagem:der_zoom.png|thumb|300px|Figura 6]] | [[Imagem:der_zoom.png|thumb|300px|Figura 6 - Erros de truncamento e precisão (zoom)]] | ||
Na figura 5, a derivada em x=3 numérica em função do <math>\Delta x</math> utilizado. O valor exato da derivada em é <math>f'(3)=-4.08963</math>. Diminuindo o valor do incremento, vemos que em volta de <math>\Delta x = 0.01</math> começa a convergir, piorando a partir de <math>\Delta x = 10^{-6}</math>. Para valores muito pequenos temos o erro de arredondamento e para valores muito alto temos o erro de truncamento. | Na figura 5, a derivada em x=3 numérica em função do <math>\Delta x</math> utilizado. O valor exato da derivada em é <math>f'(3)=-4.08963</math>. Diminuindo o valor do incremento, vemos que em volta de <math>\Delta x = 0.01</math> começa a convergir, piorando a partir de <math>\Delta x = 10^{-6}</math>. Para valores muito pequenos temos o erro de arredondamento e para valores muito alto temos o erro de truncamento. | ||
Edição das 14h13min de 7 de outubro de 2011
A derivada de uma função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} é definida como um processo de limite, o qual é matematicamente descrito por:
| Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(x)=\lim_{\Delta x\to 0}{f(x+\Delta x)-f(x)\over \Delta x}} | (Eq. 1) |
Numericamente é impossível tomarmos o limite Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x\to 0} ; temos necessariamente que trabalhar com um valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x} finito. Portanto, a todo cálculo numérico de uma derivada será associado um erro numérico. Abaixo veremos dois métodos numéricos para calcular derivadas e estimaremos os erros associados a tais métodos.
Derivada à direita
Este método se baseia na definição formal de derivada. Para um dado valor de incremento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x} , podemos estimar a derivada da função:
| Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(x) \approx {f(x+\Delta x)-f(x)\over \Delta x}} | (Eq. 2) |
A expressão a direita é chamada de quociente diferencial de Newton. Existem duas fontes de erro nessa expressão, o erro de arredondamento e o erro de truncamento. O primeiro é um erro associado à precisão numérica dos computadores, que é finita (o número de casas dos números). Comparando a expressão (2) com a (1), notamos que, quanto menor o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x} , o valor estimado numericamente é mais próximo ao valor real. No entanto, numericamente não podemos tomar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x} tão pequeno quanto se queira, porque há um limite de precisão numérica. Assim, na região do Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x} pequeno há o tipo de erro chamado de erro de arredondamento.
Por exemplo, se o nosso computador hipotético processar uma operação matemática com 4 casas decimais, temos que, para a função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) = x^2 } , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(0,1) = 0,01} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(0,1001) = 0,01002001} . Note que, usando a precisão de nosso computador, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) = f(x+\Delta x)} no caso em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = 0,01} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x = 0,001} . Com isso, o resultado da derivada numérica seria Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f\, '(0,1) = 0} , o que sabemos não ser verdade, já que podemos calcular essa derivada analiticamente. Isso coloca um limite inferior para o incremento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x} , e assim para a precisão da estimativa numérica da derivada.
O segundo tipo de erro podemos dizer que é "intrínseco" ao método numérico. Para estimá-lo, faremos uso da expansão em série de Taylor da função :Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(x)}
| Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x+\Delta x) = f(x) + f'(x)\Delta x + \frac{1}{2}f''(x)(\Delta x)^2 + \frac{1}{6}f'''(x)(\Delta x)^3 + ...} | (Eq. 3) |
manipulando os termos acima, temos:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle {f(x+\Delta x)-f(x)\over \Delta x} = f' + \frac{1}{2}f''\Delta x + ... \, ,}
e assim
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f' = \underbrace{{f(x+\Delta x)-f(x)\over \Delta x}}_{Quociente\; de\; Newton} - \frac{1}{2}f''\Delta x + ... \, .}
Comparando a expressão acima com o método de de derivada à direita , Eq. 2, notamos que a diferença existe a partir do termo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x} . Podemos dizer que o erro ao usar a quociente de Newton para calcular a derivada é proporcional à Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x} . Assim, vemos que o erro cresce linearmente com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x} e portanto devemos usar valores pequenos do incremento.
Resumindo, por um lado temos o erro de truncamento e pelo outro o de arredondamento, onde o valor ótimo será uma solução de compromisso entre os dois tipos de erro. Vemos então que deve haver um intervalo de valores dentro do qual o Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x} deve variar para que a derivada numérica seja a mais próxima do valor real possível. Nas figuras 5 e 6 mostramos um exemplo.
Derivada Centrada
Outro cálculo numérico da derivada pode ser feito baseado na declividade de dois pontos próximos, um antes e outro depois do ponto onde queremos avaliar a derivada.
A declividade da linha definida por esses dois pontos é:
| Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(x)\approx {f(x+\Delta x)-f(x-\Delta x)\over 2\Delta x}} | (Eq. 4) |
que é chamada de derivada centrada.
Podemos mostrar que o erro intrínseco a este método é menor do que o erro associado ao método anterior. Para estimar o erro de truncamento, expandimos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) } em torno de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x} ( feito na Eq(3)) e em torno de :
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x-\Delta x) = f(x) + f'(x)(-\Delta x) + \frac{1}{2}f''(x)(-\Delta x)^2 - {1\over 6}f'''(x)(\Delta x)^3 + ...}
Somando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x+\Delta x) } dada pela Eq.(3) e os termos de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x-\Delta x) } da expressao acima, notamos que os termos lineares em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\Delta x} se cancelam. Isolando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(x)} , temos:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(x) = \underbrace{{f(x+\Delta x)-f(x-\Delta x)\over 2\Delta x}} -{2\over 6}f'''(x)(\Delta x)^2 + ...}
Comparando a expressão acima com a definição do método de derivada centrada, Eq. 4, notamos que o erro de truncamento é da ordem de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\Delta x)^2} . Para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Delta x| < 1 } , vemos que o erro de truncamento associado ao método de derivada centrada é menor do que o erro para a derivada à direita.
Medida numérica do Erro associado a cada método
Para ter uma estimativa do erro associado a utilização da derivada numérica, podemos comparar valores utilizando uma função que tem sua derivada conhecida analiticamente. Assim, o erro é dado por
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle erro = {|f'_{AN}(x) - f'_{NUM}(x)| \over |f'_{NUM}(x)|}, }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'_{AN}(x)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'_{NUM}(x)} são as derivada analítica e numérica de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) } , respectivamente.
Note que, multiplicando o erro por 100, temos a porcentagem de erro que acompanha a derivada numérica.
Programa
Implementar a derivada numérica em FORTRAN é apenas uma linha de código:
...
Df = (f(x+h) - f(x))/h
...
Onde f(x) deve ser definida num bloco FUNCTION F(x) ... END FUNCTION F.
O resto depende de onde e para que queremos calcular a derivada.
Exemplo
Como demonstração, usaremos a função Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} dada por
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) = \frac{\sin(x^2) e^{x/3}}{\sqrt{x^2+4}}.}
Os gráficos abaixo ilustram os métodos de derivada à direita (figuras 1 e 2) e derivada centrada (figuras 3 e 4), ambos com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0,6} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x = 0,4} .
Primeiramente, a figura 1 mostra a derivada à direita, onde a curva em vermelho representa Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} e a curva em azul representa a derivada de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} .
A figura 2 mostra um zoom no ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} com a curva da derivada calculada pelo método descrito acima. Em azul a derivada calculada numericamente, só que agora com um deslocamento em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} para passar pelo ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (f(x),x)} .
O exemplo do método de derivada centrada está representado na figura 3. Em vermelho a curva e em azul a sua derivada.
A figura 4 mostra um zoom com a curva da derivada centrada em .
Além da ilustração dos métodos de derivação numérica, as figuras 5 e 6 mostram o gráfico do valor retornado pelo método da derivação à direita em função do incremento utilizado.
Na figura 5, a derivada em x=3 numérica em função do utilizado. O valor exato da derivada em é . Diminuindo o valor do incremento, vemos que em volta de começa a convergir, piorando a partir de . Para valores muito pequenos temos o erro de arredondamento e para valores muito alto temos o erro de truncamento.
Na figura 6 vemos ampliada a região de convergência, onde o valor de parece ser o ótimo.
NOTA: os programa FORTRAN usado para o calculo da derivada esta em Real (ou Real*4, ou seja ponto flutuante em representação de 32 bits). Como seria em dupla precisão (Real*8)?