Shooting method e Método de Crank-Nicolson

O objetivo deste trabalho é aplicar o Shooting method (método do chute) para encontrar as primeiras funções de onda espaciais da Equação de Schrödinger para o caso do poço de potencial infinito. Após, será realizada a evolução temporal através do Método de Crank-Nicolson.

Equação de Schrödinger

A equação de Schrödinger unidimensional pode ser escrita da seguinte maneira:

$i\hbar {\frac {\partial \Psi }{\partial t}}=-{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}\Psi }{\partial x^{2}}}+V\Psi .$

Para resolvê-la é necessário efetuar uma separação de variáveis:

$\Psi (x,t)=\psi (x)\varphi (t).$

Aplicando na primeira equação e separando os termos espaciais dos termos temporais, chega-se a uma equação com o seguinte formato:

$i\hbar {\frac {1}{\varphi }}{\frac {d\varphi }{dt}}=-{\frac {\hbar ^{2}}{2m}}{\frac {1}{\psi }}{\frac {d^{2}\psi }{dx^{2}}}+V.$

Pelo fato da parte da esquerda ser dependente de t e a parte da direita ser dependente de x e de ambas estarem relacionadas por uma igualdade, é necessário que ambos os lados sejam constantes: em outras palavras, não é possível modificar um lado sem necessariamente alterar o outro. Através de um raciocínio perspicaz, a constante em questão será denominada E.

Parte temporal

A parte que diz respeito à evolução temporal:

${\frac {d\varphi }{dt}}=-{\frac {iE}{\hbar }}\varphi .$

A solução geral possui o seguinte formato

$\varphi (t)=Ce^{-{\frac {-iEt}{\hbar }}},$

cuja constante C pode, neste caso, ser absorvida, de modo que

$\varphi (t)=e^{-{\frac {-iEt}{\hbar }}}.$

Parte espacial

Quanto à parte espacial, utilizando o mesmo raciocínio empregado anteriormente, a equação pode ser escrita como

$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}+V\psi =E\psi$

Para este caso, no entanto, não há uma única solução, pois esta depende do potencial V escolhido. Para o presente trabalho optou-se por trabalhar com o caso do poço infinito de potencial pelo fato das soluções analíticas já serem conhecidas, de modo a tornar possível avaliar os resultados numéricos obtidos à luz da solução analítica.

Poço de potencial infinito

Esquematicamente, tem-se:

Poço de potencial infinito

O potencial pode ser descrito como:

$V(x)={\begin{cases}0,&{\mbox{se }}0\leq x\leq L,\\\infty ,&{\mbox{de outra forma.}}\end{cases}}$

Dentro do poço, onde $V=0$, o problema pode ser modelado da seguinte maneira

$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}=E\psi ,$

ou

${\frac {d^{2}\psi }{dx^{2}}}=-k^{2}\psi ,$

onde

$k\equiv {\frac {\sqrt {2mE}}{\hbar }}.$

A solução é dada por

$\psi (x)=Asen(kx)+Bcos(kx).$

Aplicando as condições de contorno $\psi (0)=\psi (L)=0$ e efetuando a normalização da função de onda, obtém-se a solução geral

$\psi _{n}(x)={\sqrt {\frac {2}{L}}}sen\left({\frac {n\pi }{L}}x\right),$

cujas energias discretizadas são

$E_{n}={\frac {\hbar ^{2}k_{n}^{2}}{2m}}={\frac {n^{2}\pi ^{2}\hbar ^{2}}{2mL^{2}}}.$

Utilizando a equação acima, pode-se calcular os valores da energia de cada estado estacionário. Para o caso de um elétron, as energias referentes aos três estados estacionários são $E_{1}=0,376$ eV, $E_{2}=1,504$ eV e $E_{3}=3,384$ eV.

Na próxima seção será feita uma estimativa dos valores acima expostos através do "Shooting method".

Shooting Method

Muitos métodos numéricos (e.g. Runge-Kutta, Forward Euler) requerem os valores da função e de sua derivada no ponto inicial. Acontece que podem haver problemas em que estes valores não estarão disponíveis, principalmente o valor da derivada em questão. Uma alternativa seria conjecturar o valor da condição inicial e integrar, através de um método apropriado, em direção à outra condição de contorno: um "chute" apropriado faria com que a integração evoluísse e retornasse um valor muito próximo, a depender da acurácia necessária, ao da condição de contorno. A ideia seria executar os seguintes passos:

1. Supor um valor para a condição de contorno desconhecida (e.g. $y(0)$ ou $y'(0)$);
2. Integrar o problema através de um método conhecido até a próxima condição de contorno (e.g., $y(L)$);
3. Se o chute inicial não fez com que o sistema evoluísse até $y(L)$, então deve-se supor outro valor para a condição inicial e repetir o procedimento.

O método descrito acima de forma simplificada recebe o nome, em inglês, de Shooting method, o que em português seria algo como "Método do tiro" ou "Método do chute". Na próxima seção esse método será aplicado para o caso do poço infinito de potencial.

Poço de potencial infinito

Seja a equação ${\frac {d^{2}\psi }{dx^{2}}}=-k\psi E$, onde $k={\frac {2m}{\hbar ^{2}}}$.

Escrevendo com outra notação: ${\ddot {\psi }}=-k\psi E$.

Dividindo o problema em $\Delta x$'s pequenos, pode-se reescrever a equação acima da seguinte forma:

${\ddot {\psi }}={\frac {\Delta {\dot {\psi }}}{\Delta x}}={\frac {{\dot {\psi _{2}}}-{\dot {\psi _{1}}}}{\Delta x}}\implies {\dot {\psi _{2}}}={\ddot {\psi }}\Delta x+{\dot {\psi _{1}}}$

.

Também:

${\dot {\psi }}={\frac {\Delta \psi }{\Delta x}}={\frac {\psi _{2}-\psi _{1}}{\Delta x}}\implies \psi _{2}={\dot {\psi }}\Delta x+\psi _{1}$

.

Além disso:

$\Delta x=x_{2}-x_{1}\implies x_{2}=x_{1}+\Delta {x}$

.

A integração, então, é realizada utilizando as relações 8, 9, 10 e 11, até que se atinja a borda do poço, isto é, $x=L$.

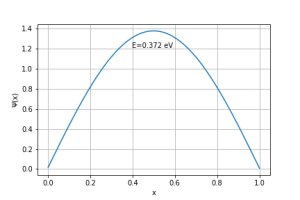
Com a discretização acima, foi possível implementar o algoritmo. Das condições de contorno do problema, sabe-se que $\psi (0)=0$, de modo que $\psi _{1}=0$. No entanto, o valor da derivada ${\dot {\psi _{1}}}$ não é conhecido, de modo que supõe-se que seja uma constante, a saber, ${\dot {\psi _{1}}}=1$. Chutando que $E=0$, utilizando a massa do elétron e $L=1$, obtém-se a primeira solução estacionária:

Solução estacionária (n=1)

Pode-se observar que o valor de energia obtido numericamente é cerca de 4% menor do que aquele obtido analiticamente.

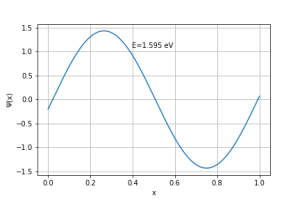
Para o caso n=2:

Solução estacionária (n=2)

Aqui, o valor obtido numericamente é aproximadamente 5% maior do que o valor obtido analiticamente.

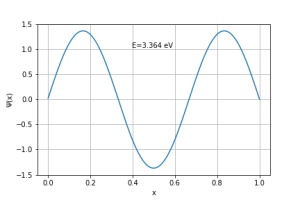
Para o caso n=3:

Solução estacionária (n=3)

Para este caso, o valor numérico é cerca de 1% menor do que o valor analítico.