Equação de Langevin

Artur Uhlik Fröhlich e Leonardo Dasso Migotto

O objetivo deste trabalho é resolver computacionalmente a equação de Langevin utilizando o método BAOAB Serão explorados os casos de partículas individuais livres, estudando os efeitos da variação do coeficiente de atrito no deslocamento quadrático médio e no momentum médio.

Equação de Langevin

Esta equação diferencial estocástica descreve a evolução de um sistema quando sujeito a forças do tipo determinísticas e estocásticas simultâneamente. A sua aplicação mais popular é relativa ao movimento Browniano, o movimento de uma partícula macroscópica imersa em um fluído, sujeita à força de atrito excercida pelas partículas microscópicas do fluído. Neste caso, a equação pode ser escrita como:

${\frac {d{\vec {v}}}{dt}}=-\gamma {\vec {v}}+\xi (t).$

Na equação acima, $\gamma$ é o coeficiente de atrito e $\xi (t)$ é um ruído estocástico branco, que segue o Teorema Central do Limite com média 0 e deslocamento padrão relacionado à temperatura, a Constante de Boltzmann, $\gamma$ e a massa da partícula. A partir desta expressão, é possível descobrir a relação do coeficiente de difusão do fluído e os valores envolvidos na equação:

$D={\frac {2k_{B}T}{\gamma m}}.\quad (I)$

Onde $D$ é o coeficiente de difusão do meio, $k_{B}$ é a constante de Boltzmann, $T$ é a temperatura e $m$ é a massa da partícula macroscópica. Outra relação presente no livro do Frenkel , desenvolvida teoricamente, é a do coeficiente de difusão e o deslocamento quadrático médio de uma partícula no meio:

$\left\langle \left(r(t)-r_{0}(t)\right)^{2}\right\rangle =2dDt.\quad (II)$

Método BAOAB

O método numérico escolhido para realizar a integração da equação é conhecido como BAOAB, desenvolvido por Leimkuhler e Mattews utilizado para resolver equações diferenciais estocásticas.

Ele é baseado na solução exata para o momentum,

$d{\vec {p}}=-\gamma {\vec {p}}dt+{\sqrt {2\gamma mk_{B}T}}d{\vec {W}},$

e faz o uso de um método de separação das equações entre as denominadas A, B e O, respectivamente representadas:

${\vec {r}}\left(t+{\frac {\Delta t}{2}}\right)={\vec {r}}(t)+{\frac {\Delta t}{2}}{\vec {p}}\left(t+{\frac {\Delta t}{2}}\right){\frac {1}{m}},$

${\vec {p}}\left(t+{\frac {\Delta t}{2}}\right)={\vec {p}}(t)+{\frac {\Delta t}{2}}{\vec {f}}(t),$

${\vec {p'}}\left(t+{\frac {\Delta t}{2}}\right)=exp(-\gamma \Delta t){\vec {p}}\left(t+{\frac {\Delta t}{2}}\right)+{\sqrt {1-exp(-2\gamma \Delta t)}}{\sqrt {mk_{B}T}}{\vec {G}}.$

O ${\vec {G}}$ aqui representa um número aleatório Gaussiano que faz o papel do ruído estocástico.

A equação "A" realiza meio passo no tempo da distância, a "B" realiza um meio passo para o momentum e o "O" contabiliza a contribuição estocástica equação.

Essas equações podem formar vários algoritmos de integração mas o utilizado nesse trabalho será o BAOAB:

${\vec {p}}\left(t+{\frac {\Delta t}{2}}\right)={\vec {p}}(t)+{\frac {\Delta t}{2}}{\vec {f}}(t),\quad (1)$

${\vec {r}}\left(t+{\frac {\Delta t}{2}}\right)={\vec {r}}(t)+{\frac {\Delta t}{2}}{\vec {p}}\left(t+{\frac {\Delta t}{2}}\right){\frac {1}{m}},\quad (2)$

${\vec {p'}}\left(t+{\frac {\Delta t}{2}}\right)=exp(-\gamma \Delta t){\vec {p}}\left(t+{\frac {\Delta t}{2}}\right)+{\sqrt {1-exp(-2\gamma \Delta t)}}{\sqrt {mk_{B}T}}{\vec {G}},\quad (3)$

${\vec {r}}(t+\Delta t)={\vec {r}}\left(t+{\frac {\Delta t}{2}}\right)+{\frac {\Delta t}{2}}{\vec {p'}}\left(t+{\frac {\Delta t}{2}}\right){\frac {1}{m}},\quad (4)$

${\vec {p}}(t+\Delta t)={\vec {p'}}\left(t+{\frac {\Delta t}{2}}\right)+{\frac {\Delta t}{2}}{\vec {f}}(t).\quad (5)$

É importante lembrar que entre os dois últimos passos é necessário atualizar o termo ${\vec {f}}$, já que ele pode depender de termos já atualizados como ${\vec {p}}$ ou ${\vec {r}}$.

Implementação do Método BAOAB

Um exemplo de implementação desse método feito foi para a partícula livre. Nota-se que nesse caso a partícula não é afetada por um campo potencial então os passos do método que envolvem a força ${\vec {f}}$ serão desconsiderados.

A função a seguir se encontra em um código (orientado a objeto) de autoria do integrante Artur e que pode ser acessado aqui.

    def baoab_livre(self, dt, exp, sqexp, sqt, G):
        '''
        dt: discretização do tempo
        exp: termo referente a primeira exponencial da eq.3
        sqexp: termo da raiz quadrada com exponencial da eq.3
        sqt: termo da raiz quadrada com a Temperatura da eq.3
        G: o vetor G da eq.3
        '''
        # 1/2 passo da distância
        self.pos[0] += self.vel[0]*(dt/2)
        self.pos[1] += self.vel[1]*(dt/2)
        # Passo estocástico
        self.vel[0] = exp*self.vel[0] + sqexp*sqt*G[0]
        self.vel[1] = exp*self.vel[1] + sqexp*sqt*G[1]
        # Atualização final da posição
        self.pos[0] += self.vel[0]*(dt/2)
        self.pos[1] += self.vel[1]*(dt/2)

Essa função representa um passo do laço temporal utilizando o método BAOAB. Os atributos em forma de lista ".pos" e ".vel" representam as componentes x e y respectivamente da posição e velocidade do objeto partícula.

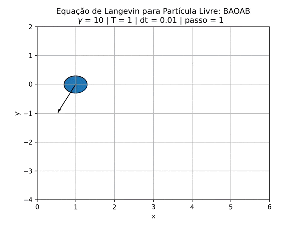
Um exemplo de funcionamento do código é a animação a seguir:

Simulação de uma partícula livre sob o efeito da Equação de Langevin.

O código foi executado usando a semente de números aleatórios 420.

Parâmetros das Simulações

A fim de estudar a implementação do Método BAOAB para a Equação de Langevin para uma partícula livre, nove simulações foram executadas com parâmetros bem definidos. Utilizando unidades reduzidas, os parâmetros recebidos pelo computador foram:

$m,k_{B}=1$

$\Delta t=10^{-2}$

$t_{max}=5\cdot 10^{5}$

${\vec {r}}_{ini}=(0,0)$

${\vec {p}}_{ini}=(0,0)$

$\gamma =10^{-1},10^{0},10^{1}$

$T=1,2,3$

As nove simulações englobam, ao todo, todas combinações de $T$ e $\gamma$ para os valores escolhidos. Após todos os $50.000.001$ instantes da simulação serem calculados, o computador salva os valores de posição e momentum de cada um deles em arquivos numa pasta única, que contem, além destes valores, os valores utilizados na simulação. Assim, um programa diferente pode ser utilizado para continuar a execução da simulação ou também gerar gráficos dos valores salvos de posição e momentum. Isso permite uma análise facilitada dos dados, pois não requer a execução completa do programa para cada gráfico que se deseja criar.

Como esta é uma simulação com uma variável estocástica, alguns cuidados são extremamente importantes para fazer a execução correta da simulação. Os seguintes fatos devem ser tidos em mente ao executar simulações desta natureza:

- As simulações devem sempre possuir sementes aleatórias diferentes, com pouquíssimas exceções. Utilizando os nossos programas de exemplo: caso os valores de $T$ e $\gamma$ fossem trocados, mas a semente aleatória não, estaríamos utilizando os mesmos valores aleatórios para calcular o termo estocástico da equação, não gerando simulações completamente independentes. Além do mais, a "grande sacada" dessas simulações é que elas devem conseguir ser analisadas independente das sementes aleatórias.

- Simulações com $\Delta t$ diferentes, porém todas outras variáveis iguais (incluindo a semente aleatória) não são equivalentes. Utilizando os nossos programas de exemplo: caso o $\Delta t$ mude, o número de números aleatórios a ser gerado será diferente, portanto ambas simulações, aparentemente equivalentes, terão ruídos aleatórios completamente diferentes e, portanto, não poderão ser comparadas tradicionalmente.

Implementação da Graficação do Momentum

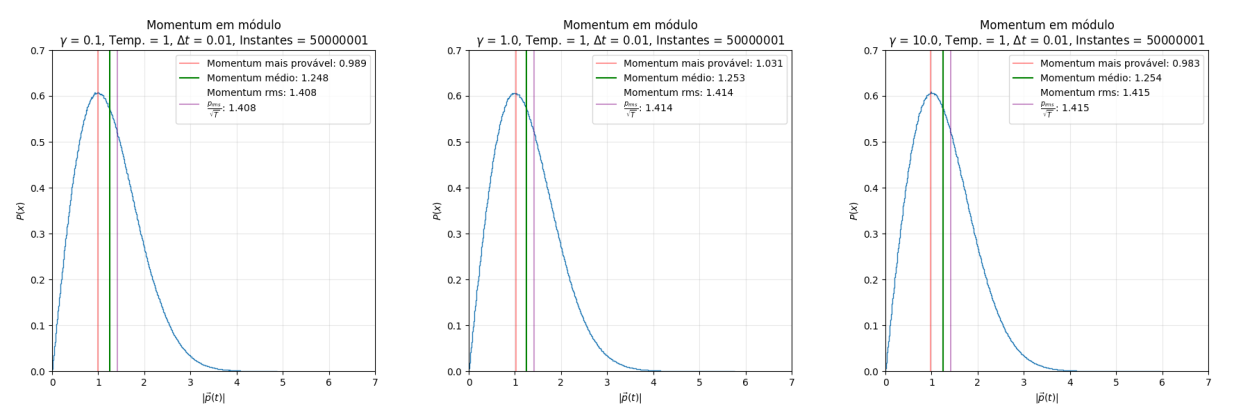
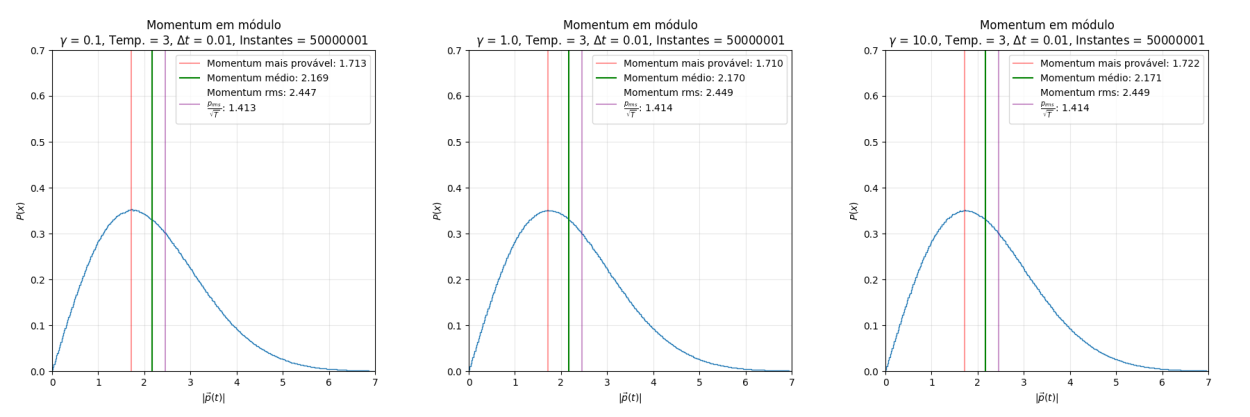
Os gráficos a seguir foram construídos fazendo um histograma normalizado dos momenta da partícula em todos os instantes, e mostram a função de densidade de probabilidade do momentum da partícula para um dado instante de tempo. Isto é, o valor do eixo $y$ mostra a probabilidade de que a partícula possua a velocidade indicada no eixo $x$, de modo que:

$\int _{0}^{+\infty }p(x)dx=1.$

Análise do Momentum

Implementação do Deslocamento Quadrático Médio

Segue abaixo uma implementação do cálculo do deslocamento quadrático médio. A partir de um array de posições de uma única partícula, o código faz os cálculos necessários retornando um array com o MSD em cada instante de tempo, além de outras coisas.

A função a seguir se encontra em um código de autoria do integrante Leonardo. Este código abre os dados gerados por outro programa, que salva todas informações em arquvios, e permite visualizar propriedades como o MSD, a distribuição do momentum, entre outras coisas.

if modo == "MSD":
    novotamanho = int(1 + ((nsalvos-1)/divisoes))
    desviodividido = np.zeros(novotamanho)
    indice = novotamanho - 1
    xx = xy[:, 0]
    yy = xy[:, 1]
    for i in range(divisoes):
        xini = xx[i*indice]
        yini = yy[i*indice]
        dx = xx[i*indice : 1+(i+1)*indice] - xini
        dy = yy[i*indice : 1+(i+1)*indice] - yini
        desviodividido += dx**2 + dy**2
    desviodividido = (desviodividido/divisoes)[1:]
    eixox = np.linspace(0, int(tmax/divisoes), int((nsalvos - 1)/divisoes) + 1)[1:]
    difusivo = desviodividido[int(10/(dt*gaminha)):]
    dezao = np.mean(difusivo/eixox[int(10/(dt*gaminha)):])/4
    eixox = np.log10(eixox)
    desviodividido = np.log10(desviodividido)
    balistico = desviodividido[:int(1/(dt*gaminha))]
    difusivo = desviodividido[int(10/(dt*gaminha)):]
    bal = np.polyfit(eixox[:int(1/(dt*gaminha))], balistico, 1)
    dif = np.polyfit(eixox[int(10/(dt*gaminha)):], difusivo, 1)
    reta1 = bal[0]*eixox + bal[1]
    reta2 = dif[0]*eixox + dif[1]

Neste código, "xy" é um array bidimensional, onde os índices da primeira dimensão representam o tempo, e a segunda dimensão possui dois índices: um para a posição em $x$ e outro para a posição em $y$. Para melhorar a precisão do MSD, o programa permite "fatiar" o array original de posições, considerando cada fatia das distâncias como uma execução do programa independente (o número de fatias é a variável "divisoes", definida ao iniciar o programa). Um número maior de fatias resulta em um tempo reduzido percorrido pela partícula em cada fatia, porém retorna dados com maior precisão.

Após definir a posição relativa de cada fatia dentro do array original, o programa itera sobre ele, calculando os valores de MSD para cada instante de cada fatia e somando-os a um array vazio. Por fim, é feito a média dos MSDs pelo número de partículas neste array. Dado o modo preferido de visualizar os dados posteriormente e a necessidade de outras análises numéricas, o array é transformado para escala logarítmica. É importante destacar que, antes de transformar os arrays de tempo e MSD para a escala logarítmica, ambos perdem o valor de índice 0: isso é importante pois, ao transformar os tempos para esta escala, o valor do $Log_{10}0=-\infty$, e este valor é impossível de ser calculado computacionalmente.

Em seguida, dois arrays criados a partir do do MSD: um deles contém somente pontos do período de difusão balística, enquanto o outro possui pontos da difusão normal. É feita a regressão linear de cada um destes conjuntos de daods, a fim de encontrar a inclinação das retas ajustadas aos dados (e confirmar que estes períodos possuem, de fato, essas características difusivas, como veremos a seguir).

Estas informações são posteriormente colocadas em um gráfico utilizando outras funções. Estes gráficos poderão ser vistos na próxima seção.

Análise do MSD

Os resultados a serem analisados são originados do código (procedural) do integrante Leonardo.

Foram executadas diferentes vezes a simulação para compararmos a influência do $\gamma$ e da temperatura no deslocamento quadrático médio.

Temperaturas de 1-3 e $\gamma =0.1$:

Temperaturas de 1-3 e $\gamma =1$:

Temperaturas de 1-3 e $\gamma =10$:

De início pode-se notar que o ${\vec {r^{2}}}$ escala de maneira proporcional a $t^{2}$ (balístico) no início do processo, e depois de um determinado tempo obtemos uma relação linear que é a parte difusiva do processo. Essas inclinações das retas nos regimes balístico e difusivo são constantes em relação ao $\gamma$ e à temperatura. Outro aspecto constante é a temperatura, que não gera aparente diferença nos gráficos de MSD (mas no valor do coeficiente de difusão sim)

Uma referência da literatura a respeito do MSD (mas no contexto de dinâmica molecular usando o potencial de Lennard-Jones) se encontra no livro do Frenkel, expressa por essa imagem:

A partir da figura pode-se notar que a inclinação das retas representantes dos regimes balístico e difusivo são 2 e 1, valores esses encontrados pelas simulações realizadas.

Outro aspecto importante a se ressaltar é a concordância do cálculo do coeficiente de difusão através da equação (I) e da relação de Einstein em (II), obtida através dos pontos presentes na parte difusiva.

Uma relação interessante encontrada foi a maneira como escala a mudança de regimes, indicada pela reta perpendicular ao eixo do tempo. Podemos encontrar uma aproximação para o tempo em que o regime difusivo inicia na simulação a partir da relação dependente de $\gamma$:

$\Omega ={\frac {10}{\gamma }}$