Oscilações Acopladas/Problema de Fermi-Pasta-Ulam-Tsingou: mudanças entre as edições
| Linha 13: | Linha 13: | ||
A abordagem adotada no presente trabalho é a seguinte: inicialmente, serão apresentados alguns resultados teóricos bem conhecidos de osciladores acoplados lineares. A seguir, compararemos esses resultados com simulações computacionais. [falta complementar] | A abordagem adotada no presente trabalho é a seguinte: inicialmente, serão apresentados alguns resultados teóricos bem conhecidos de osciladores acoplados lineares. A seguir, compararemos esses resultados com simulações computacionais. [falta complementar] | ||
== Osciladores Acoplados | == Osciladores Lineares Acoplados== | ||
<center> | <center> | ||
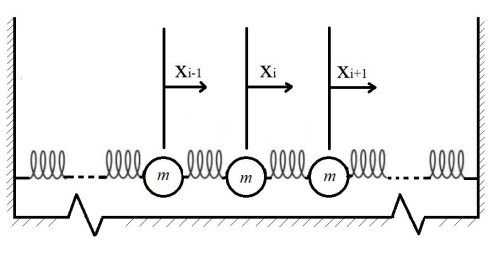
<li style="display: inline-block;">[[Arquivo: | <li style="display: inline-block;">[[Arquivo:OLA-modelo-geral.jpg|500px|left|thumb|center|'''Figura 1.''' Ilustração de um modelo geral de oscilações acopladas . ]]</li> | ||
</center> | </center> | ||
Edição das 16h25min de 28 de abril de 2022
Grupo: Paula Pandolfo, Ramiro de Souza e Wallace Carvalho
Objetivo: Este trabalho tem dois objetivos principais: apresentar alguns resultados analíticos de osciladores lineares acoplados, comparando esses resultados com simulações computacionais; e implementar o modelo de osciladores acoplados com a adição de um termo quadrático, conforme inicialmente apresentado pelo artigo original do problema de Fermi-Pasta-Ulam-Tsingou (FPUT), analisando os resultados. Apresentaremos algumas simulações dos casos bidimensionais, mas a análise de resultados será restrita aos casos unidimensionais, por simplicidade. Inicialmente será introduzido o formalismo de oscilações acopladas lineares. [falta complementar]
Introdução
Os osciladores são talvez os sistemas mais estudados na Física, sendo capazes de modelar uma ampla gama de fenômenos, como, p. ex., pêndulos, circuitos eletrônicos, interações moleculares. O comportamento linear desses sistemas, em particular, possui resultados analíticos bem conhecidos.
O problema de FPUT (Enrico Fermi, John R. Pasta, Stanislaw M. Ulam, Mary Tsingou) resulta da análise computacional de um sistema de partículas que apenas interagem com seus vizinhos, com interações modeladas por oscilações acopladas com a adição de um termo não-linear, que pode ser quadrático ou cúbico. O intuito original da simulação era estudar como esse sistema evolui para o equilíbrio térmico. Se as forças fossem estritamente lineares, a energia alocada em cada modo de vibração não se distribuiria entre os demais modos, ou seja, não se atingiria o equilíbrio térmico. Entretanto, com a adição dos termos não lineares, pelo Teorema da Equipartição da Energia, supunha-se que, após um certo tempo, a energia total do sistema seria distribuída uniformemente entre os modos normais de vibração, o que significaria que o sistema teria atingido o equilíbrio térmico. Entretanto, isso não foi observado.
O caso foi estudado pela primeira vez em Los Alamos, nos Estados Unidos, e implementado no computador MANIAC I (Mathematical Analyzer Numerical Integrator and Automatic Computer Model I). Além dos três participantes coautores do artigo que relatou o caso em 1955, Mary Tsingou implementou o código e resolveu numericamente o sistema. Atualmente, por essa razão, o paradoxo é denominado pela sigla FPUT (Fermi-Pasta-Ulam-Tsingou).
A abordagem adotada no presente trabalho é a seguinte: inicialmente, serão apresentados alguns resultados teóricos bem conhecidos de osciladores acoplados lineares. A seguir, compararemos esses resultados com simulações computacionais. [falta complementar]
Osciladores Lineares Acoplados
Referências
Bibliografia principal
- C. Gros, "Complex and Adaptive Dynamical Systems". Springer-Verlag, Berlim, 2015.
- H. Sayama, "Introduction to the Modeling and Analysis of Complex Systems". Open SUNY Textbooks, Geneseo, NY, 2015.