Motility-Induced Phase Separation(MIPS)

Grupo: Bernardo Boatini e Murilo Kessler Azambuja

Introdução

A matéria ativa é um tipo de sistema fora do equilíbrio termodinâmico, onde cada "partícula" ou "agente" do sistema tem a capacidade dissipar energia na forma de forças mecânicas exercidas sobre o ambiente no qual está imerso. Esses sistemas muitas vezes podem exibir vários fenômenos novos, como movimentos coletivos quando exige-se um alinhamento das partículas (Como bio-polímeros que se auto organizam, tipo os microtúbulos que são parte do citoesqueleto celular, ou cardumes de peixe, por exemplo), ou os chamados MIPS (Motility-Induced Phase Separation) que são sistemas que apresentam uma mudança de fase física devido à interações que proíbem a ocupação simultânea de um volume do espaço por duas partículas simultâneas. Nestes sistemas, os agentes possuem a capacidede de auto-propulsão, de forma que a condição de balnço detalhado é quebrada no nível microscópico, uma vez que as partículas possuem uma direção preferencial de movimento.Estes tipos de sistema muitas vezes podem ser tratados a partir de uma abordagem hidrodinâmica, na qual são chamados de fluidos ativos, e divergem do comportamento usual de fluidos compostos de matéria usual inativa, os quais são descritos pela equação de Navier-Stokes.

Apesar desses sistemas fundamentalmente quebrarem a condição do balanço detalhado, ainda não é claro se o comportamento estatístico universal de sistemas de fluidos ativos necessariamente divergem daqueles de de sistemas em equilíbrio. A investigação de comportamentos universais nestes tipos de sistema, além de ser um interece central na física, também pode nos permitir utilizar conhecimentos já bem conhecidos (como a transição de fase em sistemas de matéria em equilíbrio termodinâmico) para descrever sistemas novos. Neste trabalho foi reproduzido o artigo (COLOCAR A REFERÊNCIA) onde foi investigada o comportamento crítico de um sistema com MIPS e se viu que este tipo de sistema pertence à classe de universalidade de sistemas em equilíbrio como o modelo de Ising para spin. Para tal, foi utilizada três abordagens diferentes: um modelo hidrodinâmico, uma descrição baseada em teoria de campos e a simulação de um modelo de rede hexagonal.

Modelo

O sistema geral que estamos interessados em descrever é constituído de um conjunto de partículas em um meio com friccção, i.e, em um sistema sem conservação de momentum e com interações que não permitem a ocupação simultânea de duas partículas em um mesmo sítio (FIG. 1).

FIGURA 1: Imagem retirada de (COLOCAR A REFERÊNCIA). Em (a) vemos a difusão devido à rotação da direção de movimento preferencial da partícula, em (b) temos o "movimento balístico" (seta verde) e a difusão devido à translação da partícula (setas azuis) e, em (c), vemos a interação entre partículas em sítios vizinhos, impedindo a ocupação simultânea do mesmo sítio por duas partículas.

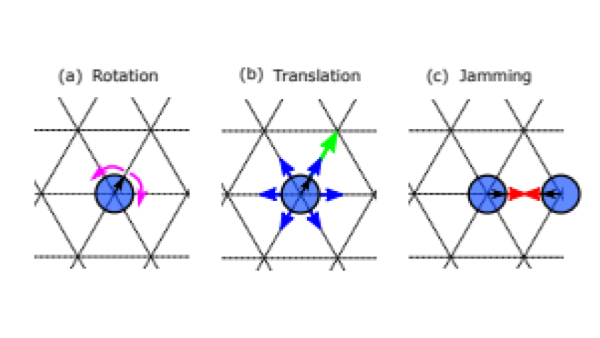
Uma forma de modelar este sistema é considerá-lo um fluido ativo polar e compressível sem interações de alinhamento entre partículas, de forma que não se espera observar movimentos coletivos. Tal sistema é descrito de forma contínua pela chamada equação de Toner-Tu.

De um ponto de vista microscópico, podemos usar uma formulação discreta baseada na teoria de campos. Neste caso, consideramos uma rede hexagonal bidimensional, com o numero de ocupação de cada sítio da rede restringido por uma constante $M$ (futuramente diremos que $M=1$, de forma que apenas uma partícula pode ocupar cada sítio).

Modelo no Continuo

As equações de Tuner-Tu são dadas por (COLOCAR REFERÊNCIA)

$\partial _{t}\rho +\nabla \cdot \mathbf {g} =0\qquad (1a)$

$\partial _{t}\mathbf {g} =-\zeta \nabla \rho -\kappa \mathbf {g} +\mu \nabla ^{2}\mathbf {g} +\mathbf {f} \qquad (1b)$

Mostrar e explicar a equação de Toner-Tu

Modelo no Discreto

Mostrar e explicar(ou falar por cima) da abordagem de campo discreto

Implementação

Em modelos do tipo LGCA(Lattice Gas Celular Automata) o tipo de rede, bem como as topologias usadas, podem ser determinantes para as medidas e caracterizações do estado macroscópico. A simetria hexagonal se mostra uma boa alternativa para aumentar os graus de liberdade de uma partícula numa rede, quando comparada com a simetria quadrada. Na geometria hexagonal, assim como na quadrada, todos os sítios vizinhos possuem uma mesma distancia entre si só que com 6 graus de liberdade ao invés de quatro.

Existem duas topologias possíveis em uma rede hexagonal: "zigzag" e "armchair", e a diferença das duas esta principalmente na implementação das condições de contorno periódicas. No caso da topologia em "zigzag", o espaço é representado em um paralelogramo, e existem 4 direções em que cruzando uma parede

Sub-Box Sampling Method

Explicar o método das sub caixas

Medida 1

Explicar a medida 1

Medida 2

Explicar a medida 2

Resultados

Mostrar e explicar os Resultados

Referência