Equação de Águas Rasas: mudanças entre as edições
| Linha 764: | Linha 764: | ||
==== Resultados ==== | ==== Resultados ==== | ||
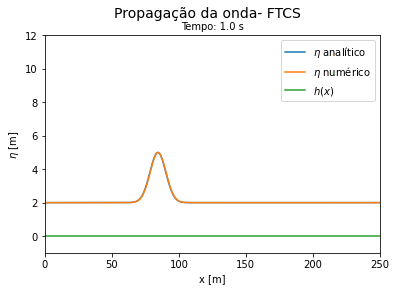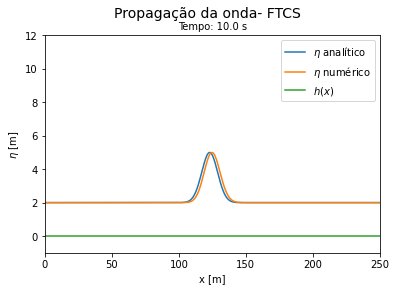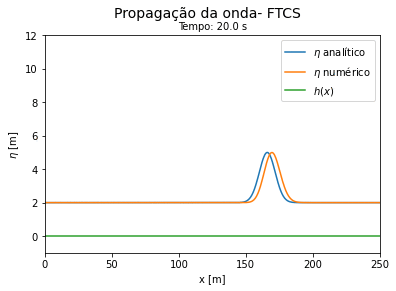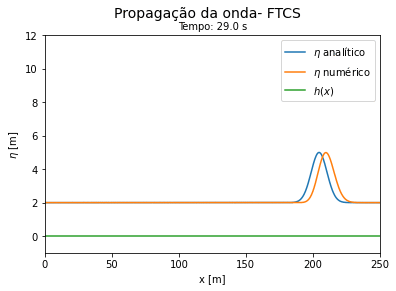
'''Exemplo 1. Onda confinada em uma caixa com profundidade constante''': utilizando que a superfície é constante e que tanto a velocidade quanto altura da onda são inicialmente funções gaussianas centradas no espaço, obtemos a evolução no espaço que pode ser vista no GIF abaixo. | '''Comparação entre a solução exata e a numérica''': para verificar se o cálculo das equações de águas rasas utilizando FTCS explícito e implícito estão funcionando, partimos da situação simplificada das equações dadas por (-) e (-). Neste problema consideramos a velocidade e a profundidade constantes com os valores respectivos de 2.3 m/s e 2 m. O deslocamento de água inicial é representado por uma Gaussiana centrada em 80m, de amplitude 2 m e largura 70 m, nesta situação a solução analítica de (39) é dada por: | ||
<math> \eta = 2 + 3 \cdot exp \Big(-\frac{((x-80) -ut))^2}{70} \Big) </math> | |||
Do código 2 obtemos as seguintes curvas ao longo do tempo. Vemos que a solução numérica por FTCS explícito se aproxima do resultado analítico para tempos curtos e se afasta da solução exata a medida que o tempo avança. | |||
[[Arquivo:Aguas rasas FTCS explicito.gif|thumb|400px|center|Comparação entre a solução exata e a numérica por FTCS explícito. Forma conservativa.]] | |||
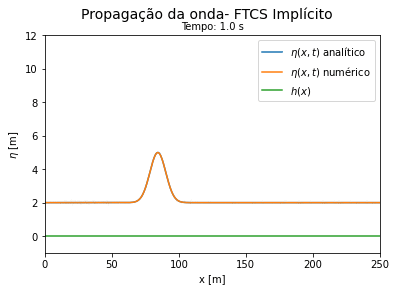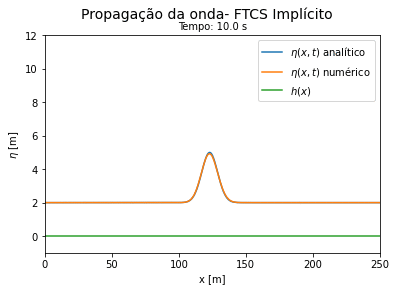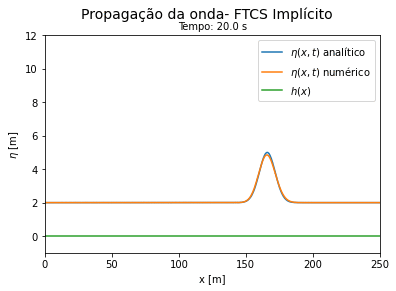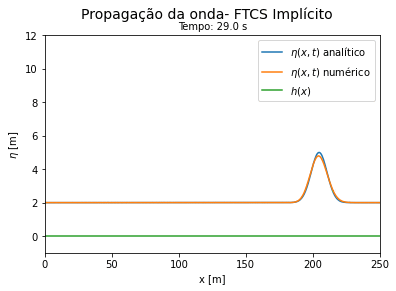
Do código 3 obtemos as seguintes curvas ao longo do tempo. Vemos que a solução numérica por FTCS implícito se aproxima do resultado analítico para tempos curtos e se afasta da solução exata a medida que o tempo avança, porém de forma mais lenta que o método explícito. | |||
[[Arquivo:Aguas rasas FTCS implicito.gif|thumb|400px|center|Comparação entre a solução exata e a numérica por FTCS implícito. Forma conservativa.]] | |||
'''Exemplo 1. Onda confinada em uma caixa com profundidade constante''': através do código 1, utilizando que a superfície é constante e que tanto a velocidade quanto altura da onda são inicialmente funções gaussianas centradas no espaço, obtemos a evolução no espaço que pode ser vista no GIF abaixo. | |||
[[Arquivo:conservativa-gausiana.gif|thumb|400px|center|Evolução da amplitude da onda em uma caixa. Forma conservativa]] | [[Arquivo:conservativa-gausiana.gif|thumb|400px|center|Evolução da amplitude da onda em uma caixa. Forma conservativa]] | ||
Edição das 08h26min de 19 de outubro de 2021
Grupo: Gabriel Schmökel e Julia Remus
Em construção
Introdução
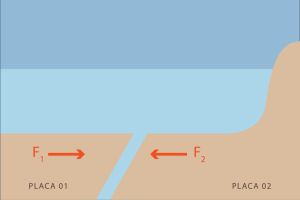
Tsunami é um fenômeno da natureza caracterizado por uma sucessão de ondas marinhas, que devido ao seu grande volume e alta velocidade, podem se tornar catastróficas ao atingir a costa. Sismos, erupções vulcânicas, deslizamentos de terra, impactos e outros movimentos submarinos são a causa para a formação deste evento, sendo a grande maioria provocado pelos movimentos das placas tectônicas.
Formação de um Tsunami
Vamos analisar a sequência de passos da formação de uma Tsunami formada a partir de um abalo sísmico. [1]
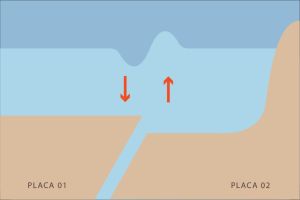
I. A convergência das placas tectônicas, devido as correntes de convecção, faz com que existam forças de tensão entre as placas.
A tensão entre as placas eventualmente ultrapassa o limite máximo, o que provoca o deslizamento brusco de uma das placas sobre a outra, gerando um grande deslocamento de volume de água na vertical. Como a tsunami ocorre em grandes profundidades, ela pode passar despercebida para um barco que navega nas proximidades, uma vez que amplitude da onda é menor.
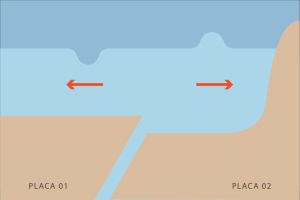
II. A onda gerada se propaga ao longo de todas as direções do plano da água.
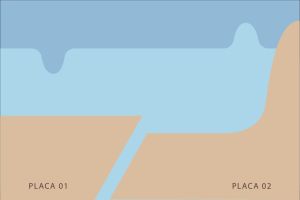
III. A medida que a onda se aproxima da superfície ela diminui sua velocidade e aumenta sua amplitude
Temos o interesse de descrever fisicamente a propagação da Tsunami de acordo com a topografia da água e do mar, por essa razão não iremos estudar o efeito físico que causou o deslocamento do volume de água.
Descrição Física
As equações de águas rasas são as equações físicas que descrevem o fenômeno do Tsunami, em uma dimensão elas são dadas por:
Na representação do fluxo de descarga estas equações se tornam:
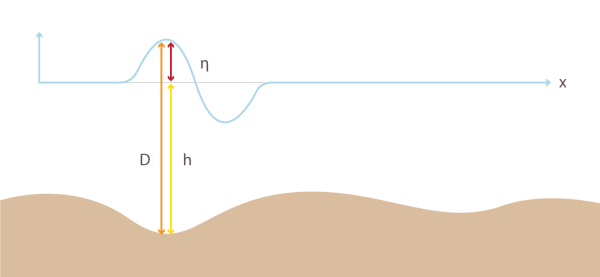
As componentes da equação de águas rasas podem ser melhor interpretadas através da seguinte figura:
corresponde a amplitude da onda, determina a profundidade do mar em repouso, é o deslocamento total da água, é a velocidade do fluído e é o fluxo de descarga.
Teoria
Derivação das Equações de Águas Rasas
Iremos demonstrar como chegamos nas equações de águas rasas em duas dimensões, nas formas conservativa e dissipativa, em representações do fluxo de descarga e de velocidade. Posteriormente, tendo as equações em 2D, iremos simplificar elas para a forma unidimensional. Neste processo de demonstração, iremos explicar o significado físico de cada quantidade presente nas equações.
Para obter as equações de águas rasas devemos partir da equação da continuidade e das equações da quantidade de movimento de Navier-Stokes:
A equação da continuidade em (5) descreve o balanço de massas para os elementos de volume infinitesimais que pertencem ao fluído, onde a quantidade do lado esquerdo da equação informa o fluxo de massa que entra e sai pelo elemento de volume, e a quantidade do lado direito está relacionada com a massa que se acumula ao longo do tempo [2]. Nesta expressão é a densidade, e é o campo de velocidades, onde u,v e w são as velocidades das partículas que compõe o fluído nas direções x,y,z.
As equações de Navier-Stokes em (6) são balanços diferenciais da quantidade de movimento, obtidas através da aplicação da segunda lei de Newton em cada ponto do escoamento [3] [4] [5].
- é a aceleração da partícula fluída ao longo do campo de velocidade .
- está associado as tensões tangenciais e normais atuando sobre os elementos de volume ( é o tensor tensão, as componentes deste tensor são as tensões normais e tangenciais de cisalhamento, expressas por , no qual indica a direção e o plano normal).
- está associado as pressões que atuam sobre os elementos do fluído.
- é o vetor aceleração da gravidade atuando sobre os elementos infinitesimais de volume do fluído.
Introduzindo as condições de contorno para a superfície e para a profundidade do oceano [6]:
, onde
, onde
é o deslocamento vertical da água sobre a superfície em repouso, é o vetor velocidade do fluído nas direções horizontais x e y.
A equação da continuidade em (5) pode ser simplificada pelo fato do fluído ser incompressível, isto implica que a densidade é constante.
Integrando a expressão da continuidade em (9), utilizando a regra da integral de Leibniz [7], com os limites indo de até chegamos na seguinte expressão:
Teorema de Leibniz:
Substituindo as condições de contorno da profundidade (8) em (10) obtemos:
Substituindo a condição de contorno da superfície (7) em (12):
(13) é a primeira das equações das águas rasas que obtemos, onde é o comprimento da água total do fundo do oceano até a amplitude da onda. Podemos expressar (13) através do fluxo de descarga nas direções x e y, estás quantidades estão relacionadas com as velocidades da seguinte forma [8]:
Substituindo (14) e (15) em (13) chegamos na representação do fluxo de descarga para uma das equações de águas rasas.
A partir da primeira equação de águas rasas podemos determinar a taxa da variação da amplitude da onda em relação ao tempo conhecendo as taxas dos fluxos de descarga em relação as regiões espaciais.
Vamos buscar obter as outras duas equações de águas rasas restantes, a partir das quantidades de movimento de Navier-Stokes nas componentes x,y e z temos:
Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} +\frac{1}{\rho}\frac{\partial P}{\partial x} +g_x = 0 \qquad (17) }
Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} +\frac{1}{\rho}\frac{\partial P}{\partial x} +g_y = 0 \qquad (18) }
Na componente z em (19) não consideramos a aceleração das partículas, pois a aceleração da gravidade é muito maior. Também tomamos como nulo as componentes e em (17) e (18), assim passamos a definir . Neste momento não estamos desconsiderando as forças de fricção, por isso o tensor tensão também é nulo.
Resolvendo equação diferencial da componente z em (19) podemos obter a pressão, a qual é hidrostática.
Substituindo a pressão em (17):
Integrando a expressão (21), utilizando a regra da integral de Leibniz e as condições de contorno (7) e (8), com os limites indo de até chegamos em outra das equações de águas rasas:
Generalizando a equação (22), para a componente y, obtemos a última das equações de águas rasas:
Na representação de fluxo de cargas as expressões (22) e (23) são apresentadas respectivamente como:
Com as equações de águas rasas (22), (23), (24) e (25) podemos calcular as taxas de variação dos fluxos de descarga em relação ao tempo. As equações (13), (22) e (23), na representação de velocidades, e as equações (16), (24) e (25), na representação do fluxo de descargas, são as equações de águas rasas conservativas.
Iremos buscar pelas equações de águas rasas não conservativa considerando o tensor de estresse em (6). Os elementos deste tensor são responsáveis por causar nas partículas tensões tangenciais e perpendiculares, onde as tensões tangenciais são representadas por elementos onde , e as perpendiculares por elementos onde .
Decompondo nas componentes x,y, e z de presente em (6) temos:
Considerando o fluído Newtoniano, então as tensões de cisalhamento serão proporcionais a uma taxa de deformação, onde a constante de deformidade é a viscosidade.
Substituindo (29),(30) em (26), integrando em relação a componente z, utilizando a regra de Leibnz e as condições de contorno (7) e (8), obtemos:
Onde é a constante de viscosidade turbulenta, é uma força de resistividade relativa ao movimento do fluído com o fundo do oceano na direção x. Podemos negligenciar a constante de turbulência na situação em que não temos inclinações abrutas no fundo do mar [9].
Considerando que o fluído é uniforme, então a expressão para Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \frac{\tau_x}{\rho} é } é:
Onde é o coeficiente de fricção, porém o coeficiente de rugosidade de Manning é mais usado, alguns valores deste coeficiente são [10]:
| Material | Coeficiente de Rugosidade de Manning |
|---|---|
| Cimento puro e metal liso | 0,010 |
| Terra lisa | 0,017 |
| Pedras, ervas daninhas | 0,035 |
| Péssimo relevo de canal | 0,060 |
| Bom relevo de canal | 0,025 |
O coeficiente de fricção e o de rugosidade de Meanning estão relacionados por:
Substituindo (34) em (33) obtemos:
Generalizando a expressão (31) para a componente y.
Adicionando, repectivamente, (35) e (36) nas expressões (24) e (26), obtemos as equações de águas rasas considerando as forças de fricção do fundo do oceano.
As equações (16), (37) e (38), na representação do fluxo de descargas, são as equações de águas rasas não conservativas.
Em uma dimensão podemos expressar as equações de águas rasas eliminando a componente das expressões (16),(37) e tomando o fluxo de descarga como nulo.
Simplificação das Equações de Águas Rasas
As equações de águas rasas podem ser simplificadas para equação da deriva através das seguintes considerações:
- A velocidade do fluído é constante.
- A profundidade do fundo do oceano é constante.
De (39) e das considerações acima temos:
Discretização na Forma Conservativa
Um modelo mais simples - desconsiderando a fricção, viscosidade do líquido e as forças de Coriolis sobre ele - pode ser obtido [11][12]. Para desenvolvê-lo são necessárias algumas premissas:
- O comprimento da onda é muito maior que as contribuições na direção
- A aceleração na direção da velocidade na direção é zero
- As componentes das velocidades em e em ( e ) não variam em
O sistema então pode ser descrito pelas seguintes equações:
Onde é a altura do fluido desde a base, são as velocidades médias na direções , é a constante gravitacional e é função que descreve a superfície onde acontece o movimento.
Para descrever numericamente as equações de águas rasas na forma conservativa foi utilizado discretização por diferenças finitas e o método pra frente no tempo e no espaço (FTCS). As equações discretizadas podem ser observadas abaixo.
Na situação em que temos as equações de águas rasas simplificadas por (39), aplicando FTCS, a evolução temporal da amplitude da onda é:
Aplicando FTCS implícito temos:
Discretização na Forma não Conservativa
As equações de águas rasas na forma não conservativa são dadas por (16),(37) e (38), para descrever numericamente estás equações foi utilizado discretização por diferenças finitas, onde realizamos derivadas centradas na região espacial, e para frente no região temporal (FTCS).
Discretizando a expressão (16):
Discretizando a expressão (37):
Definindo as quantidades:
Das quantidades definidades e da derivada parcial do fluxo de descarga em relação ao tempo temos a respectiva avanço temporal para M:
Generalizando a expressão (52) para o fluxo de descarga N temos:
Simulações Computacionais
Forma Conservativa 1D
Para a solução em uma dimensão foi utilizado o mesmo código do conservativo 2D, porém desconsiderando a contribuição da direção .
Forma conservativa 2D
As equações (42),(43) e (44) foram implementadas em python para descrever a evolução temporal das variáveis , e .
As condições de contorno dos exemplos obedecem as expressões:
- Nos contornos de x: , discretizando essa derivada temos que:
- Nos contornos de y: , discretizando essa derivada temos que:
Código 1
O código 1 foi escrito na linguagem Python e resolve os exemplos 1 e 2 que serão apresentados abaixo.
#%% Bibliotecas
import numpy as np
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import animation
import matplotlib.patches as mpatches
from IPython.display import HTML, Image
#%% Parametros
L_xf = 10.0 # m
L_x0 = -L_xf
NX = 100
dx = (L_xf - L_x0) / NX
L_yf = 10.0 # m
L_y0 = -L_yf
NY = 100
dy = (L_yf - L_y0) / NY
N_INNER = (NX - 2) * (NY - 2)
g = 9.8 # m /s^2
# Tempo
dt = 0.002
Nt = 1500
time_interval = np.arange(0, Nt*dt, dt)
#%% Discretização do espaço x-y
x = np.linspace(L_x0, L_xf, NX-1)
y = np.linspace(L_y0, L_yf, NY-1)
X, Y = np.meshgrid(x, y)
#%% Condições iniciais, em distribuição gaussiana
sigma = 1.0
sigma_v = 1.0
h_2d = 6 * np.ones(shape=np.shape(X)) + np.exp(-(((X)**2 / 2*(sigma**2)) + ((Y)**2 / 2*(sigma**2))))
u_2d = 0.1 * np.exp(-(((X)**2 / 2*(sigma_v**2)) + ((Y)**2 / 2*(sigma_v**2))))
v_2d = 0.1 * np.exp(-(((X)**2 / 2*(sigma_v**2)) + ((Y)**2 / 2*(sigma_v**2))))
b = np.ones(shape=np.shape(X)) # Fundo da superficie constante
h_2d -= b # diminui a altura da superficie
#%% Vetores das variáveis anteriores e historico das variaveis
h_ant = np.copy(h_2d)
v_ant = np.copy(v_2d)
u_ant = np.copy(u_2d)
# Inicilização das listas para armazenar os valores
hist_h, hist_u, hist_v = [], [], []
Função para resolução das equações diferenciais com FTCS.
# Fator de multiplicacao
mx = (dt / (2*(dx)))
my = (dt / (2*(dy)))
def resolve_pdes(h, vx, vy):
"""
Função que retorna os valores de profunidade, velocidade em x e em y
no próximo tempo
Parametros
-----------
h : array
profundidade no tempo t
vx : aray
velocidade em x no tempo t
vy : array
velocidade em y no tempo t
Retorna
-----------
prox_h : array
profundidade no tempo t + dt
prox_u : array
velocidade em x no tempo t + dt
prox_v : array
velocidade em y no tempo t + dt
"""
# Inicializa os vetores para armazenarem os resultados calculados
prox_h = np.ones(shape = (np.shape(h)), dtype = np.float64)
prox_u = np.ones(shape = (np.shape(vx)), dtype = np.float64)
prox_v = np.ones(shape = (np.shape(vy)), dtype = np.float64)
# Loop nos pontos discretizados
for i in range(1, NX - 1):
for j in range(1, NY - 1):
# Alturas e velocidades conforme a posicao do ponto:
# _l : ponto a esquerda, _r: ponto a direita, _up: ponto acima, _d: abaixo
# Condicao a esquerda ------------------
if i == 1: # primeiro x interno
h_l = h[i, j]
u_l = -vx[i, j]
v_l = vy[i, j]
else:
h_l = h[i-1, j]
u_l = vx[i-1, j]
v_l = vy[i-1, j]
# --------------------------------------
# Condicao a direita -------------------
if i == NX - 2: # ultimo x interno
h_r = h[i, j]
u_r = -vx[i, j]
v_r = vy[i, j]
else:
h_r = h[i+1, j]
u_r = vx[i+1, j]
v_r = vy[i+1, j]
# --------------------------------------
# Condicao abaixo ----------------------
if j == 1: # primeiro y interno
h_d = h[i, j]
u_d = vx[i, j]
v_d = - vy[i, j]
else:
h_d = h[i, j - 1]
v_d = vy[i, j - 1]
u_d = vx[i, j - 1]
# --------------------------------------
# Condicao acima ----------------------
if j == NY - 2: # utlimo y interno
h_up = h[i, j]
u_up = vx[i, j]
v_up = - vy[i, j]
else:
h_up = h[i, j + 1]
v_up = vy[i, j + 1]
u_up = vx[i, j + 1]
# --------------------------------------
## Primeira Equação
h_ij = h[i, j] - \
(h_r * u_r - h_l * u_l) * fator_x - \
(h_up * v_up - h_d * v_d) * fator_y
prox_h[i, j] = h_ij
# ## Segunda equação
hu_ij = ((h[i, j]) * vx[i, j]) - \
mx * (
((h_r * (u_r ** 2)) + (1/2 * g * (h_r ** 2))) -\
((h_l * (u_l ** 2)) + (1/2 * g * (h_l ** 2)))
) - \
my * (
(h_up * u_up * v_up ) - (h_d * u_d * v_d)
) - \
mx * g * h[i, j] * (b[i, j+1] - b[i, j-1])
# # ## Terceira Equação
hv_ij = (h[i, j] * vy[i, j]) - \
m_x * (
(h_r * u_r * v_r) - (h_l * u_l * v_l)
) - \
my * (
((h_up * (v_up ** 2)) + (1/2 * g * (h_up ** 2))) - \
((h_d * (v_d ** 2)) + (1/2 * g * (h_d ** 2)))
) - \
my * g * h[i, j] * (b[i, j+1] - b[i, j-1])
prox_v[i, j] = hv_ij / (h_ij)
return prox_h, prox_u, prox_v
#%% Cálculo
# Resolve para cada passo de tempo
for t in time_interval:
h, u, v = resolve_pdes(h_ant, u_ant, v_ant) # valores das variaveis no tempo = t + dt
# faz isso pq tava dando um erro estranho nesses pontos?
h[0, :] = h[1, :]
h[:, 0] = h[:, 1]
v[0, :] = v[1, :]
v[:, 0] = v[:, 1]
u[0, :] = u[1, :]
u[:, 0] = u[:, 1]
# adicionar essas variáveis em listas pra conseguir plotar dps
hist_h.append(h); hist_u.append(u); hist_v.append(v)
# Coloca as variaveis atuais como anteriores pro proximo calculo
h_ant = np.copy(h)
u_ant = np.copy(u)
v_ant = np.copy(v)
#%% Gráfico
# Reorganiza os vetores para plotar
x_2d = X[0]
y_2d = Y[0]
for i in range(1,len(X)):
x_2d = np.append(x_2d, X[i])
y_2d = np.append(y_2d, Y[i])
def animate(i):
plt.clf() # limpa a figura, pra nao ficar sobrepondo figs
# titulos
plt.suptitle('Evolução da onda', fontsize=14)
plt.title(f'Tempo: {round(dt*i, 3)}', fontsize=12)
# labels
plt.ylabel('y', fontsize=8)
plt.xlabel('x', fontsize=8)
# plot
graph = plt.scatter(x_2d, y_2d, c= hist_h[0::8][i], vmin=4.5, vmax=5.5, marker='.')
plt.colorbar()
plt.savefig(f'caminho-frames/{i}.png')
return graph
# fig = plt.figure(figsize=(16,9))
# ax = fig.gca(projection='3d')
fig, ax = plt.subplots()
ani = animation.FuncAnimation(fig, animate, frames = len(hist_h[0::8]), repeat=False, interval=0.1)
#%% Salva o gif, com os frames salvos anteriormente
images = []
for i in range(len(hist_h[0::80])):
images.append(imageio.imread(f'caminho-frames/{i}.png'))
imageio.mimsave("gif2.gif", images,fps=8)
Código 2
O código 2 foi escrito na linguagem Python e serve para comparar a solução numérica de (39) com a solução analítica.
Lx = 500.0
#define o número de pontos na direção x
px = 1001
#define o espaçamento entre os pontos mais próximos
dx = Lx / (px - 1)
# Localiza o número de pontos ao longo das direções x e y
x = np.linspace(0.0, Lx, num=px)
#profundidade do oceano h = 50 m
h = 2 * np.ones_like(x)
# Condição inicial da onda gerado pelo sismo
eta0 = 3. * np.exp(-((x-80)**2/70))
eta0_analitico = 2 + 3. * np.exp(-((x-80)**2/70))
# velocidade constante
u = 4.3
# constante da gravidade
g = 9.81
# define o tempo máximo e o intervalo infinitesimal de tempo
Tmax = 30.
dt = 0.01
nt = (int)(Tmax/dt)
eta = shallow_water(eta0,eta0_analitico,h,g,nt,dx,dt,px,x,u)
def shallow_water(eta0,eta0_analitico,h,g,nt,dx,dt,px,x,u):
# Copia a amplitude inicial da onda no espaço
eta = eta0.copy()
nx = eta.shape
fundo = 0 * np.ones_like(x)
conta = 0
# Loop over timesteps
for k in range(1,nt):
eta = atualiza_eta(eta, dx, dt, nx,px,h,u)
eta0_analitico = 2 + 3. * np.exp(-((x-80 -u*(k*dt))**2/70))
conta = conta + 1
if(conta == 100):
plt.clf()
# titulos
plt.suptitle('Propagação da onda- FTCS', fontsize=14)
plt.title(f'Tempo: {round(dt*k, 3)} s', fontsize=10)
plt.ylim(-1, 12)
plt.xlim(0, 250)
plt.plot(x,eta0_analitico,label='$\eta$ analítico')
plt.plot(x, eta+h, label='$\eta$ numérico')
plt.plot(x,fundo,label='$h(x)$')
plt.xlabel('x [m]')
plt.legend()
plt.ylabel('$\eta$ [m]')
plt.show()
plt.close()
conta=0
return eta, M
def atualiza_eta(eta, dx, dt, nx, px, h, u):
for j in range(1,px-2):
D = eta + h
dDdx = u*(D[j+1] - D[j-1]) / (2. * dx)
eta[j] = eta[j] - dt * (dDdx)
return eta
Código 3
O código 3 foi escrito na linguagem Python e serve para comparar a solução numérica de (40) com a solução analítica. O código 3 muda em relação ao 2 basicamente a função atualiza_eta, por isso iremos só escrever essa parte.
def atualiza_eta(eta, dx, dt, nx, px, h, u, a, b, c, d):
eta[0]=0
d[px-1]=0
d[1] = eta[1]+((dt*u)/(2*dx))*eta[0];
d[px-2]= eta[px-2]-((dt*u)/(2*dx))*eta[px-1];
for i in range(2,px-3):
d[i]=eta[i];
for i in range(0,px-2):
a[i]= -1*((dt*u)/(2*dx))
b[i]= 1
c[i]= ((dt*u)/(2*dx))
c[1]=c[1]/b[1]
d[1]=d[1]/b[1]
for i in range(2,px-2):
d[i]=(d[i]-d[i-1]*a[i])/(b[i]-c[i-1]*a[i])
aux=c[i-1]
c[i]=c[i]/(b[i]-c[i-1]*a[i])
eta[px-2]=d[px-2]
c[px-4] = aux
for i in range(px-3,0,-1):
eta[i]=d[i]-(c[i]*eta[i+1]);
return eta
Resultados
Comparação entre a solução exata e a numérica: para verificar se o cálculo das equações de águas rasas utilizando FTCS explícito e implícito estão funcionando, partimos da situação simplificada das equações dadas por (-) e (-). Neste problema consideramos a velocidade e a profundidade constantes com os valores respectivos de 2.3 m/s e 2 m. O deslocamento de água inicial é representado por uma Gaussiana centrada em 80m, de amplitude 2 m e largura 70 m, nesta situação a solução analítica de (39) é dada por:
Do código 2 obtemos as seguintes curvas ao longo do tempo. Vemos que a solução numérica por FTCS explícito se aproxima do resultado analítico para tempos curtos e se afasta da solução exata a medida que o tempo avança.
Do código 3 obtemos as seguintes curvas ao longo do tempo. Vemos que a solução numérica por FTCS implícito se aproxima do resultado analítico para tempos curtos e se afasta da solução exata a medida que o tempo avança, porém de forma mais lenta que o método explícito.
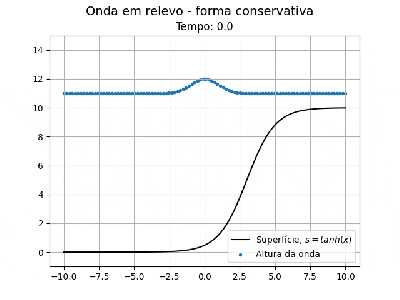
Exemplo 1. Onda confinada em uma caixa com profundidade constante: através do código 1, utilizando que a superfície é constante e que tanto a velocidade quanto altura da onda são inicialmente funções gaussianas centradas no espaço, obtemos a evolução no espaço que pode ser vista no GIF abaixo.
Exemplo 2. Onda confinada em uma caixa com profundidade variável: utilizando a função é possível simular uma onda chegando em uma praia, esse exemplo foi feito em 1D conservativo e pode ser visto abaixo.
Para realizar o código a partir do 2D conservativo mostrado acima, basta desconsiderar as derivadas em e inicializar os vetores da altura e velocidade com a discretização em apenas uma dimensão, abaixo descrita. Deve-se notar que o problema passa a ter um índice, pois a discretização não forma mais uma malha, então pode ser retirado um laço for do código.
#%% Discretização do espaço x
x = np.linspace(L_x0, L_xf, NX)
#%% Condições iniciais da superficie e da agua
# Superficie
b = 5 * np.tanh((x- L_xf*0.3) / 2) # funcao tangente
b += np.full(shape=(np.shape(b)), fill_value=-np.min(b)) # aqui é somado só para a funcao comecar em zero
# Onda e velocidade
sigma = 1.0 # distribuicao da onda
sigma_v = 1.0 # distribuicao da onda
h_2d = 1.1 * max(b) * np.ones(shape=np.shape(x)) + np.exp(-((x)**2/(2*(sigma**2))))
h_2d -= b
u_2d = 0.08 * np.exp(-((x)**2/(2*(sigma_v**2))))
Forma dissipativa 2D
Os exemplos que seguem utilizam as equações de ondas rasas (38),(43) e (44) para calcular os passos de tempo de , , , onde as funções em python atualiza_eta, atualiza_M, e atualiza_N implementam computacionalmente isto. Para implementar estas funções e outras ideias do nosso programa, o seguinte código fonte da referência [13] foi usado como base.
def atualiza_eta(eta, M, N, dx, dy, dt, nx, ny):
for j in range(1,nx-1):
for i in range(1,ny-1):
dMdx = (M[j+1,i] - M[j-1,i]) / (2. * dx)
dNdy = (N[j,i+1] - N[j,i-1]) / (2. * dy)
eta[j, i] = eta[j, i] - dt * (dMdx + dNdy)
#Condições de contorno do problema
eta[0,:] = eta[1,:]
eta[-1,:] = eta[-2,:]
eta[:,0] = eta[:,1]
eta[:,-1] = eta[:,-2]
return eta
def atualiza_M(eta, M, N, D, g, h, n, dx, dy, dt, nx, ny):
M2 = M **2 / D
MN = M * N / D
fric = g * n**2 * M * np.sqrt(M**2 + N**2) / D**(7./3.)
for j in range(1,nx-1):
for i in range(1,ny-1):
dM2dx = (M2[j+1,i] - M2[j-1,i]) / (2. * dx)
dMNdy = (MN[j,i+1] - MN[j,i-1]) / (2. * dy)
dETAdx = (eta[j+1,i] - eta[j-1,i]) / (2. * dx)
M[j, i] = M[j, i] - dt * (dM2dx + dMNdy + g * D[j,i] * dETAdx + fric[j,i])
return M
def atualiza_N(eta, M, N, D, g, h, n, dx, dy, dt, nx, ny):
MN = M * N / D
N2 = N**2 / D
fric = g * n**2 * N * np.sqrt(M**2 + N**2) / D**(7./3.)
for j in range(1,nx-1):
for i in range(1,ny-1):
dMNdx = (MN[j+1,i] - MN[j-1,i]) / (2. * dx)
dN2dy = (N2[j,i+1] - N2[j,i-1]) / (2. * dy)
dETAdy = (eta[j,i+1] - eta[j,i-1]) / (2. * dy)
N[j, i] = N[j, i] - dt * (dMNdx + dN2dy + g * D[j,i] * dETAdy + fric[j,i])
return N
A função shallow water waves recebe os parâmetros iniciais do nosso programa, executa o Loop responsável pela atualização das variáveis da amplitude da onda e do fluxo de descarga com o tempo, através da chamada das funções atualiza M,N e eta. Posteriormente, a cada 10 passagens dentro do loop um plot do sistema é feito.
def shallow_water(eta0, M0, N0, h, g, n, nt, dx, dy, dt, X, Y):
# Copia o campos de amplitude da onda, e os fluxos de descarga
eta = eta0.copy()
M = M0.copy()
N = N0.copy()
D = eta + h
# Retorna o número de pontos na direção x e y para eta
ny, nx = eta.shape
# Dividi o espaço Lx e Ly definindo os pontos nas direções x e y
x = np.linspace(0, nx*dx, num=nx)
y = np.linspace(0, ny*dy, num=ny)
limites = [np.min(x), np.max(x), np.min(y), np.max(y)]
# PLOT
plt.clf()
fig = plt.figure(figsize=(10.,6.))
plt.tight_layout()
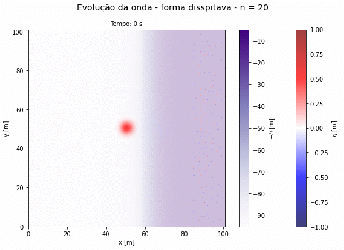
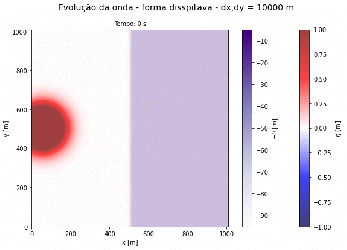
plt.suptitle('Evolução da onda - forma disspitava - n = 20.0', fontsize=14)
plt.title(f'Tempo: 0 s', fontsize=10)
# plot profundidade
fundo = plt.imshow(-h, cmap ='Purples', interpolation = 'nearest', extent = limites)
amp = plt.imshow(eta, extent = limites, interpolation = 'sinc', cmap = 'seismic', alpha= .75, vmin=-1.0, vmax= 1.0)
plt.xlabel('x [m]')
plt.ylabel('y [m]')
cbar_amp = plt.colorbar(amp)
cbar_fundo = plt.colorbar(fundo)
cbar_fundo.set_label(r'$-h$ [m]')
cbar_amp.set_label(r'$\eta$ [m]')
plt.show()
plt.close()
conta = 0
# Loop over timesteps
for k in range(1,nt):
eta = atualiza_eta(eta, M, N, dx, dy, dt, nx, ny)
M = atualiza_M(eta, M, N, D, g, h, n, dx, dy, dt, nx, ny)
N = atualiza_N(eta, M, N, D, g, h, n, dx, dy, dt, nx, ny)
D = eta + h
conta = conta + 1
if(conta == 10):
plt.clf()
fig = plt.figure(figsize=(10.,6.))
# titulos
plt.suptitle('Evolução da onda - forma disspitava - n = 20.0', fontsize=14)
plt.title(f'Tempo: {round(dt*k, 3)} s', fontsize=10)
fundo = plt.imshow(-h, 'Purples', interpolation = 'nearest', extent = limites)
amp = plt.imshow(eta, extent = limites, interpolation = 'sinc', cmap = 'seismic', alpha= 0.75, vmin=-1.0, vmax= 1.0)
plt.xlabel('x [m]')
plt.ylabel('y [m]')
cbar_amp = plt.colorbar(amp)
cbar_fundo = plt.colorbar(fundo)
cbar_fundo.set_label(r'$-h$ [m]')
cbar_amp.set_label(r'$\eta$ [m]')
conta = 0
plt.show()
plt.close()
return eta, M, N
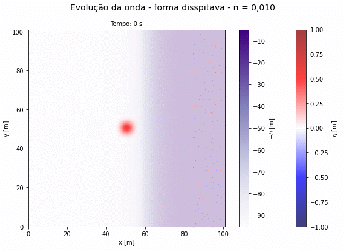
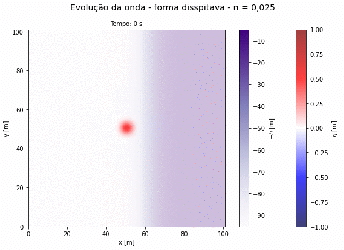
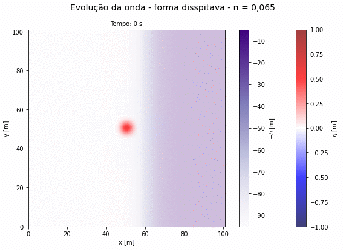
Exemplo 1 - Onda Confinada em uma Caixa
Simulação da propagação de uma onda em uma caixa de e em profundidade constante. O deslocamento do volume de água inicial é representado pela equação da Gaussiana. As condições de contorno deste problema são dadas de forma as paredes refletirem a massa do fluído.
# Define a região espacial
Lx = 100.0
Ly = 100.0
#define o número de pontos na direção x e y
px = 101
py = 101
#define o espaçamento entre os pontos mais próximos
dx = Lx / (px - 1)
dy = Ly / (py - 1)
# Localiza o número de pontos ao longo das direções x e y
x = np.linspace(0.0, Lx, num=px)
y = np.linspace(0.0, Ly, num=py)
# Plano de pontos do oceano definidos
X, Y = np.meshgrid(x,y)
#profundidade do oceano h = 50 m
h = 50 * np.ones_like(X)
# Condição inicial da onda gerado pelo sísmo
eta0 = 2. * np.exp(-((X-50)**2/10)-((Y-50)**2/10))
# Condição inicial dos fluxos de descarga
M0 = 0. * eta0
N0 = 100. * eta0
# constante da gravidade e de fricção
g = 9.81
n = 20.0
Tmax = 5.
dt = 0.01
nt = (int)(Tmax/dt)
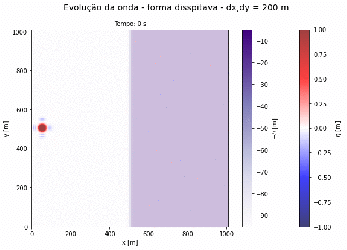
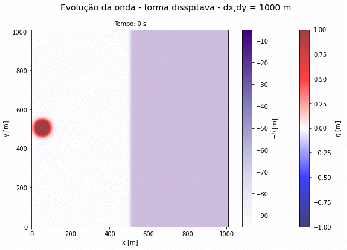
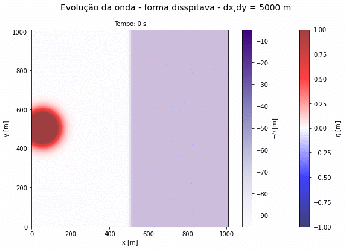
Exemplo 2.1 - Tsunami Propagando-se em Direção a Praia
Exemplo 2.2 - Tsunami Propagando-se em Direção a Praia
Simulação da propagação de uma onda em uma caixa de e em profundidade constante. O deslocamento do volume de água inicial é representado pela equação da Gaussiana. As condições de contorno deste problema são dadas de forma que as paredes refletem a massa do fluído.
Podemos observar que a medida que o fundo do oceano diminui sua profundidade a velocidade da onda também diminui, consequentemente a amplitude da onda aumenta. É observado também que para maiores comprimentos de onda da gaussiana, maior será a amplitude da onda ao chegar na praia.
Comparação entre Métodos
Onda confinada em uma caixa
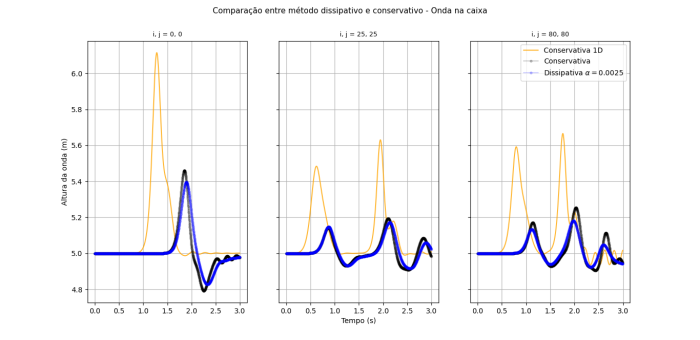
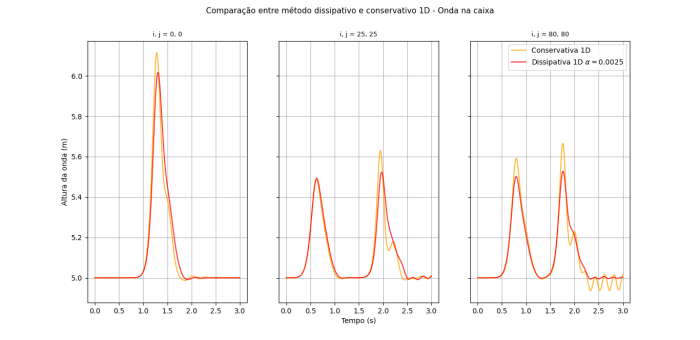
Abaixo é mostrado o gráfico de evolução temporal da altura da onda em três pontos distintos do sistema (utilizando os mesmos parâmetros que foi aplicado ao método conservativo com a onda em uma caixa de profundidade constante em todos os outros métodos). Pode-se perceber que com o passar do tempo o movimento das duas equações começa a divergir, mesmo com o fator de fricção baixo.
Para o método 1D é de se esperar que exista menos interferências entre as ondas, pois só existe parede nos finais do sistema, além disso, a onda só precisa se espalhar em uma direção, então a sua amplitude é maior.
Também é possível perceber a diferença entre métodos observando apenas em uma direção (), por causa dos termos de fricção e viscosidade.
Referências
- ↑ HOW EARTHQUAKES TRIGGER TSUNAMIS-BBC. British Broadcasting Corporation. Disponível em: https://docplayer.net/49487265-Lecture-8-the-shallow-water-equations.html
- ↑ Equação da continuidade mássica: balanços de massa diferenciais. Bloom Consultoria.Disponível em: <https://www.youtube.com/watch?v=pEip-GvO0LM&list=PL1yqHjPQz-Lqjri07DqZ3RsSWJfICvdiu&index=3>
- ↑ Equação de Navier-Stokes (Parte 1) - Derivadas materiais. Bloom Consultoria.Disponível em: https://www.youtube.com/watch?v=FLoZODPpayM
- ↑ Equação de Navier-Stokes (Parte 2) - Equação diferencial da quantidade de movimento. Bloom Consultoria.Disponível em: https://www.youtube.com/watch?v=e06ZRzdO4iM
- ↑ Equação de Navier-Stokes (Parte 3) - Tensões Normais e Cisalhantes. Bloom Consultoria.Disponível em: https://www.youtube.com/watch?v=na2kGOSYNv8
- ↑ SEGUR, Harvey; YAMAMOTO, Hiroki. Lecture 8: The Shallow-Water Equations.Disponível em: <https://docplayer.net/49487265-Lecture-8-the-shallow-water-equations.html>
- ↑ https://en.wikipedia.org/wiki/Leibniz_integral_rule
- ↑ IMAMURA, Fumihiko.Tsunami Modelling Manual.Disponível em: http://www.tsunami.civil.tohoku.ac.jp/hokusai3/J/projects/manual-ver-3.1.pdf
- ↑ http://www.tsunami.civil.tohoku.ac.jp/hokusai3/J/projects/manual-ver-3.1.pdf
- ↑ LINSLEY, Ray K.; FRANZINI, Joseph B. Water Resources Engineering.
- ↑ GARCÍA-NAVARRO, P; et al. The shallow water equations: An example of hyperbolic system. Espanha: 2008. Disponível em: <https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.571.1364&rep=rep1&type=pdf>
- ↑ KUHBACHER, Christian. Shallow Water: Derivation and Applications. Disponível em: <http://www.mathematik.tu-dortmund.de/lsiii/cms/papers/Kuehbacher2009.pdf>
- ↑ KOEHN, Daniel. 2D Shallow Water Equations. Disponível em: <https://github.com/daniel-koehn/Differential-equations-earth-system/blob/master/10_Shallow_Water_Equation_2D/01_2D_Shallow_Water_Equations.ipynb>

























































































![{\displaystyle {\dfrac {D_{i,j}^{t+\Delta t}-D_{i,j}^{t}}{\Delta t}}+\left[{\dfrac {(Du)_{i+1,j}^{t}-(Du)_{i-1,j}^{t}}{2\Delta x}}\right]+\left[{\dfrac {(Dv)_{i,j+1}^{t}-(Dv)_{i,j-1}^{t}}{2\Delta y}}\right]=0\qquad (42)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a593722950860a57b966e3200580b3e3bd08dd9)
![{\displaystyle {\dfrac {(Du)_{i,j}^{t+\Delta t}-(Du)_{i,j}^{t}}{\Delta t}}+\left[{\dfrac {(Du^{2}+{\cfrac {1}{2}}gh^{2})_{i+1,j}^{t}-(Du^{2}+{\cfrac {1}{2}}gh^{2})_{i-1,j}^{t}}{2\Delta x}}\right]+\left[{\dfrac {(Duv)_{i,j+1}^{t}-(Duv)_{i,j-1}^{t}}{2\Delta y}}\right]=-gD_{i,j}^{t}b_{x.i,j}\qquad (43)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/279191eee2e8964fd7a7979325c16e4794d3e4f1)
![{\displaystyle {\dfrac {(Dv)_{i,j}^{t+\Delta t}-(Dv)_{i,j}^{t}}{\Delta t}}+\left[{\dfrac {(Duv)_{i+1,j}^{t}-(Duv)_{i-1,j}^{t}}{2\Delta x}}\right]+\left[{\dfrac {(Dv^{2}+1/2gD^{2})_{i,j+1}^{t}-(Dv^{2}+1/2gD^{2})_{i,j-1}^{t}}{2\Delta y}}\right]=-gD_{i,j}^{t}b_{y.i,j}\qquad (44)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bd1c3c5f56c34299ec4631cd59121eeaddb9fee)