DM de potenciais descontínuos: mudanças entre as edições
| Linha 2: | Linha 2: | ||
==Evento dirigido== | ==Evento dirigido== | ||
A ideia do método para resolver o problema do força infinita é, ao invés de avançar o sistema em pequenos passos de tempo <math>dt</math>, avançar a simulação conforme as colisões forem ocorrendo. Para isso deve-se encontrar o par de partículas <math>i, j</math> que colidirá no menor intervalo de tempo entre todas as partículas, denotaremos tal intervalo por <math>dt_{min}</math>, e, então, avançar o sistema. Neste ponto teremos dois objetos colados, portanto aqui deve ser feita a mudança de velocidades de tal forma a respeitar uma colisão elástica. | A ideia do método para resolver o problema do força infinita é, ao invés de avançar o sistema em pequenos passos de tempo <math>dt</math>, avançar a simulação conforme as colisões forem ocorrendo. Para isso deve-se encontrar o par de partículas <math>i, j</math> que colidirá no menor intervalo de tempo entre todas as partículas, denotaremos tal intervalo por <math>dt_{min}</math>, e, então, avançar o sistema. Neste ponto teremos dois objetos colados, portanto aqui deve ser feita a mudança de velocidades de tal forma a respeitar uma colisão elástica. | ||
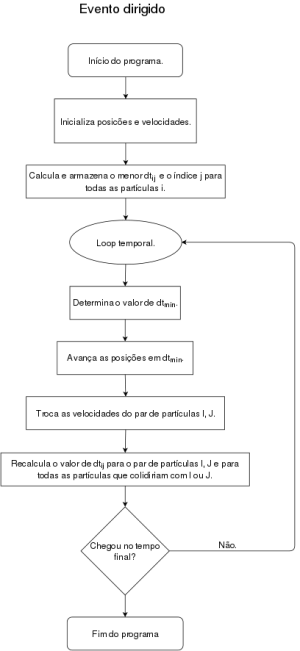
[[File:flux.png|thumb|Fluxograma de um programa simples usando o método de evento dirigido com a otimização aqui explicitada.]] | |||
===Determinação do tempo de colisão=== | ===Determinação do tempo de colisão=== | ||
Os objetos a serem usados para o cálculo do tempo de colisão entre um par de partículas <math>i, j</math> serão discos de raio <math>\sigma_i</math>, <math>\sigma_j</math>, de distância denotada por <math>\sigma</math>. Portanto, segue que a condição de colisão é: | Os objetos a serem usados para o cálculo do tempo de colisão entre um par de partículas <math>i, j</math> serão discos de raio <math>\sigma_i</math>, <math>\sigma_j</math>, de distância denotada por <math>\sigma</math>. Portanto, segue que a condição de colisão é: | ||
| Linha 23: | Linha 24: | ||
===Otimização básica=== | ===Otimização básica=== | ||
Dado uma simulação de <math> N </math> partículas, determinar o valor de <math> dt_{min} </math> é da ordem de <math> N^2 </math>, ou seja, evitar fazer esse processo todo passo de tempo economiza grande parte do tempo computacional. Uma forma simples de fazer isso é determinar e armazenar o menor <math> dt_{ij} </math> para cada partícula <math> i </math> e o índice <math> j </math> antes do loop temporal e a cada passo de tempo determinar o valor de <math> dt_{min} </math> a partir dos <math> dt_{ij} </math> armazenados. Assim, a cada passo de tempo seria necessário apenas atualizar o valor de <math> dt_{ij} </math> das partículas <math> i, j </math> e das que colidiriam com <math> i </math> ou <math> j </math>. | Dado uma simulação de <math> N </math> partículas, determinar o valor de <math> dt_{min} </math> é da ordem de <math> N^2 </math>, ou seja, evitar fazer esse processo todo passo de tempo economiza grande parte do tempo computacional. Uma forma simples de fazer isso é determinar e armazenar o menor <math> dt_{ij} </math> para cada partícula <math> i </math> e o índice <math> j </math> antes do loop temporal e a cada passo de tempo determinar o valor de <math> dt_{min} </math> a partir dos <math> dt_{ij} </math> armazenados. Assim, a cada passo de tempo seria necessário apenas atualizar o valor de <math> dt_{ij} </math> das partículas <math> i, j </math> e das que colidiriam com <math> i </math> ou <math> j </math>. | ||
Edição das 22h40min de 18 de junho de 2016
Dinâmica molecular de potenciais descontínuos é uma abordagem computacional utilizada para determinar o movimento de partículas duras que só interagem por forças de contato. Assim, fica evidente a diferença entre o potencial Lennard-Jones pois este se baseia em uma interação de curto alcance, como é mostrado em DM: um primeiro programa. Para entender como as colisões ocorrem, conhecer a forma do potencial a ser estudado é vital. Como estamos considerando corpos rígidos, ou seja, que não sofrem deformação, percebe-se que a força de contato entre as partículas será infinita e o tempo de interação zero, o que torna impossível a descrição do problema a partir de uma integração de movimento simples. O método utilizado, a ser explicitado aqui, que resolve este problema é o evento dirigido.
Evento dirigido
A ideia do método para resolver o problema do força infinita é, ao invés de avançar o sistema em pequenos passos de tempo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dt} , avançar a simulação conforme as colisões forem ocorrendo. Para isso deve-se encontrar o par de partículas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i, j} que colidirá no menor intervalo de tempo entre todas as partículas, denotaremos tal intervalo por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dt_{min}} , e, então, avançar o sistema. Neste ponto teremos dois objetos colados, portanto aqui deve ser feita a mudança de velocidades de tal forma a respeitar uma colisão elástica.
Determinação do tempo de colisão
Os objetos a serem usados para o cálculo do tempo de colisão entre um par de partículas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i, j} serão discos de raio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_i} , Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_j} , de distância denotada por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} . Portanto, segue que a condição de colisão é:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\vec{r_i}(t + dt_{ij}) - \vec{r_j}(t + dt_{ij})| = \sigma}
Com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_i} sendo o vetor posição da partícula Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dt_{ij}} o tempo de colisão entre as partículas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i, j} . Tal condição nos leva a determinação de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dt_{ij}} a partir da expressão:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dt_{ij} = \begin{cases} \infty & \quad \text{se } d < 0 \\ \infty & \quad \text{se } \Delta r . \Delta v > 0 \\ -\frac{\Delta \vec{r} . \Delta \vec{v} + \sqrt{d}}{\Delta \vec{v} . \Delta \vec{v}} & \quad \text{nos demais casos} \end{cases} }
Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle d \equiv (\Delta \vec{r} . \Delta \vec{v})^2 - (\Delta \vec{v} . \Delta \vec{v})(\Delta \vec{r} . \Delta \vec{r} - \sigma^2) }
, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \vec{r} = \vec{r_i} - \vec{r_j} }
e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \vec{v} = \vec{v_i} - \vec{v_j} }
.
Com isso, consegue-se determinar o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dt_{min} }
encontrando o menor valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dt_{ij} }
.
Mudança de velocidade em uma colisão elástica
Para fazer a mudança de velocidades temos que considerar o caso de colisão elástica entre as partículas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i, j } , sendo impulso dado por:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{J} = \frac{2m_im_j(\Delta \vec{r} . \Delta \vec{v})}{\sigma^2(m_i + m_j)}\Delta \vec{r} } .
Assim, a variação de velocidades pode ser determinada por:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \vec{v_i} = -\frac{\vec{J}}{m_i} } e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \vec{v_j} = \frac{\vec{J}}{m_j} } .
Otimização básica
Dado uma simulação de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N } partículas, determinar o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dt_{min} } é da ordem de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N^2 } , ou seja, evitar fazer esse processo todo passo de tempo economiza grande parte do tempo computacional. Uma forma simples de fazer isso é determinar e armazenar o menor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dt_{ij} } para cada partícula Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } e o índice Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j } antes do loop temporal e a cada passo de tempo determinar o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dt_{min} } a partir dos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dt_{ij} } armazenados. Assim, a cada passo de tempo seria necessário apenas atualizar o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle dt_{ij} } das partículas Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i, j } e das que colidiriam com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } ou Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle j } .