Clusterização: mudanças entre as edições
(teoria e tal) |
|||
| Linha 1: | Linha 1: | ||
'''PÁGINA EM CONSTRUÇÃO''' | '''PÁGINA EM CONSTRUÇÃO''' | ||
== Clusterização do Modelo de Ising == | == Clusterização do Modelo de Ising == | ||
=== | O modelo de Ising é definido como uma malha de tamanho L, quadrada quando em duas dimensões e cúbica quando em três dimensões, onde cada vértice apresenta um componente de spin de magnitude fixa que pode apontar para cima ou para baixo (+1 ou -1, respectivamente). O sistema pode ser descrito pelo seguinte hamiltoniano: | ||
<math>H_{Ising} = -J \sum_{\langle ij \rangle} s_i s_j</math> | |||
onde <math>s</math> representa o valor do spin e a soma é feita sobre os pares de vértices próximas que são conectadas com um acoplamento ferromagnético de força <math>J > 0</math>. | |||
Para um modelo de Ising bidimensional (o tipo que consideramos) é possível calcular sua temperatura crítica exata como: | |||
<math>T_c = \frac{2J}{\log(1 + \sqrt{2})} \simeq 2.269J</math> | |||
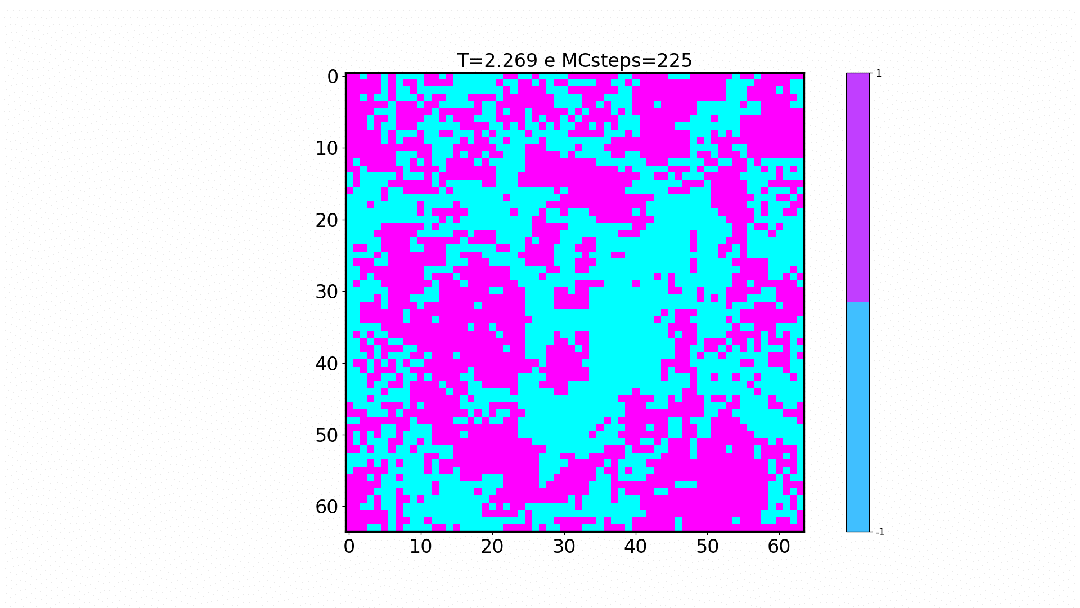
Acima dessa temperatura o sistema está na ‘’’fase paramagnética‘’’, onde a magnetização média é nula, e abaixo dessa temperatura o sistema está na fase ‘’’fase ferromagnética’’’, onde a maioria dos spins se alinham e a magnetização se torna não-nula. Ao estudar o modelo de Ising em geral temos maior interesse no comportamento do sistema perto de <math>T_c</math>, onde o sistema forma grupos grandes de spins para cima ou para baixo. Esses grupos contribuem muito para a energia do sistema, causando muita flutuação quando ''flipam''. | |||
O algoritmo de Metropolis é um ótimo algoritmo para realizar simulações do modelo de Ising. Porém, sua dinâmica de ''flip'' único é ineficiente especialmente quando próxima da temperatura crítica do sistema. As imprecisões estatísticas de quantidades como magnetização e energia interna do sistema aumentam quando próximo da temperatura crítica. Assim, quando esses grandes grupos de spins alinhados (clusters) ''flipam'', há grandes imprecisões. Essa imprecisão aumenta com o tamanho das flutuações, mas diminui com o número de medidas feitas na simulação, então para se estudar a região perto de <math>T_c</math> de modo mais preciso é necessário que a simulação aconteça por mais tempo. Porém, uma outra fraqueza do algoritmo de Metropolis é seu tempo de correlação <math>\tau</math> grande ao redor da temperatura crítica. Isso significa que o número de medidas de uma simulação é pequena, então para diminuir as imprecisões estatísticas causadas pelas poucas medidas é necessário rodar o algoritmo por mais tempo. | |||
Uma das propriedades do modelo de Ising é o fato de flutuações grandes gerarem medidas mais imprecisas. Porém, o tempo de correlação e o modo como ele se comporta próximo a <math>T_c</math> é uma propriedade do algoritmo utilizado para estudar o sistema, e então é algo que pode ser otimizado. | |||
=== Expoentes Críticos === | |||
Para estudar mais sobre a eficiência dos algoritmos no modelo de Ising podemos definir a temperatura reduzida como: | |||
<math>t = \frac{T - T_c}{T_c}</math> | |||
Essa grandeza indica o quão distante estamos da temperatura crítica <math>T_c</math>, de modo que para <math>t=0</math> estamos em <math>T_c</math>. A partir disso, e sabendo que <math>\xi</math> indica a largura médio dos clusters, temos que a expressão <math>\xi \sim |t|^{- \nu}</math> demonstra a divergência da largura de correlação (largura dos clusters). Se tratando do tempo, definimos <math>\tau \sim |t|^{-z \nu}</math> como o tempo de correlação da simulação, medido em passos de Monte Carlo por sítio da rede. O expoente <math>z</math>, chamado de expoente dinâmico, é um modo de quantificar a diferença de tempo que acontece devido à divergência. Um valor grande de <math>z</math> simboliza que <math>\tau</math> fica grande, por exemplo, fazendo uma simulação mais demorada e menos precisa quando próximo de <math>T_c</math>. | |||
Combinando as duas equações vistas, podemos escrever que <math>\tau \sim \xi^z</math>. Essa relação indica que o tempo de correlação aumenta com o tamanho típico dos clusters. Considerando um sistema de tamanho finito porém (os tipos de sistema que simulamos), o valor máximo de <math>\xi</math> vai ser o tamanho <math>L</math> do sistema (e.g. um sistema <math>64</math>x<math>64</math> tem <math>L=64</math>). Podemos assim concluir que <math>\tau \sim L^z</math>. | |||
Sabendo a temperatura crítica do sistema (para Ising 2D, <math>T_c = 2.269J</math> é possível usar a relação <math>\tau \sim L^z</math> para medir <math>z</math> por meio de simulações onde a temperatura do sistema é igual à temperatura crítica para vários tamanhos diferentes de <math>L</math>, plotando <math>\tau</math> versus <math>L</math> em escala logarítmica. A inclinação da reta que liga todos esses pontos nos dá o valor de <math>z</math>. | |||
Por meio desse método, temos que o <math>z</math> do algoritmo de Metropolis é <math>z = 2.1655 \pm 0.0012</math> e o <math>z</math> do algoritmo de Wolff (um algoritmo de clusterização) é <math>z = 0.25 \pm 0.001</math>. | |||
O motivo do tempo grande do algoritmo de Metropolis é a divergência do tamanho de correlação <math>\xi</math> próximo da temperatura crítica. Ao se aproximar de <math>T_c</math>, grandes regiões se formam onde todos os spins estão alinhados, e é demorado para que o algoritmo ''flipe'' essas regiões, dado que ele ''flipa'' os spins sítio por sítio. | |||
Algoritmos de cluster, como o de Wolff, fazem uso da técnica de clusterização. Com isso, os algoritmos encontram agrupam spins alinhados em clusters que apontam para a mesma direção e ''flipam'' os spins desse cluster ao mesmo tempo. Algoritmos de clusterização permitem uma exploração mais efetivo do espaço de fase próximo da temperatura crítica por serem mais eficientes e de precisarem de menos iterações para terem medidas precisas. | |||
=== Balanço Detalhado === | === Balanço Detalhado === | ||
Para respeitarmos o Balanço Detalhado, precisamos que a mudança da rede de um estado $<math>\nu</math> para um estado <math>\mu</math> ocorra com a mesma probabilidade da mudança de um estado <math>\mu</math> para <math>\nu</math>, denotamos essa mudança por: <math>A(\mu \to \nu) = A(\nu \to \mu)</math>, com <math>A(x \to y)</math> sendo a razão de aceitação da mudança de um estado <math>x</math> para um estado <math>y</math>. | Para respeitarmos o Balanço Detalhado, precisamos que a mudança da rede de um estado $<math>\nu</math> para um estado <math>\mu</math> ocorra com a mesma probabilidade da mudança de um estado <math>\mu</math> para <math>\nu</math>, denotamos essa mudança por: <math>A(\mu \to \nu) = A(\nu \to \mu)</math>, com <math>A(x \to y)</math> sendo a razão de aceitação da mudança de um estado <math>x</math> para um estado <math>y</math>. | ||
Edição das 18h14min de 28 de maio de 2021
PÁGINA EM CONSTRUÇÃO
Clusterização do Modelo de Ising
O modelo de Ising é definido como uma malha de tamanho L, quadrada quando em duas dimensões e cúbica quando em três dimensões, onde cada vértice apresenta um componente de spin de magnitude fixa que pode apontar para cima ou para baixo (+1 ou -1, respectivamente). O sistema pode ser descrito pelo seguinte hamiltoniano:
onde representa o valor do spin e a soma é feita sobre os pares de vértices próximas que são conectadas com um acoplamento ferromagnético de força Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle J > 0} .
Para um modelo de Ising bidimensional (o tipo que consideramos) é possível calcular sua temperatura crítica exata como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c = \frac{2J}{\log(1 + \sqrt{2})} \simeq 2.269J}
Acima dessa temperatura o sistema está na ‘’’fase paramagnética‘’’, onde a magnetização média é nula, e abaixo dessa temperatura o sistema está na fase ‘’’fase ferromagnética’’’, onde a maioria dos spins se alinham e a magnetização se torna não-nula. Ao estudar o modelo de Ising em geral temos maior interesse no comportamento do sistema perto de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} , onde o sistema forma grupos grandes de spins para cima ou para baixo. Esses grupos contribuem muito para a energia do sistema, causando muita flutuação quando flipam.
O algoritmo de Metropolis é um ótimo algoritmo para realizar simulações do modelo de Ising. Porém, sua dinâmica de flip único é ineficiente especialmente quando próxima da temperatura crítica do sistema. As imprecisões estatísticas de quantidades como magnetização e energia interna do sistema aumentam quando próximo da temperatura crítica. Assim, quando esses grandes grupos de spins alinhados (clusters) flipam, há grandes imprecisões. Essa imprecisão aumenta com o tamanho das flutuações, mas diminui com o número de medidas feitas na simulação, então para se estudar a região perto de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} de modo mais preciso é necessário que a simulação aconteça por mais tempo. Porém, uma outra fraqueza do algoritmo de Metropolis é seu tempo de correlação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} grande ao redor da temperatura crítica. Isso significa que o número de medidas de uma simulação é pequena, então para diminuir as imprecisões estatísticas causadas pelas poucas medidas é necessário rodar o algoritmo por mais tempo.
Uma das propriedades do modelo de Ising é o fato de flutuações grandes gerarem medidas mais imprecisas. Porém, o tempo de correlação e o modo como ele se comporta próximo a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} é uma propriedade do algoritmo utilizado para estudar o sistema, e então é algo que pode ser otimizado.
Expoentes Críticos
Para estudar mais sobre a eficiência dos algoritmos no modelo de Ising podemos definir a temperatura reduzida como:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = \frac{T - T_c}{T_c}}
Essa grandeza indica o quão distante estamos da temperatura crítica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} , de modo que para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=0} estamos em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} . A partir disso, e sabendo que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} indica a largura médio dos clusters, temos que a expressão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi \sim |t|^{- \nu}} demonstra a divergência da largura de correlação (largura dos clusters). Se tratando do tempo, definimos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau \sim |t|^{-z \nu}} como o tempo de correlação da simulação, medido em passos de Monte Carlo por sítio da rede. O expoente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} , chamado de expoente dinâmico, é um modo de quantificar a diferença de tempo que acontece devido à divergência. Um valor grande de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} simboliza que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} fica grande, por exemplo, fazendo uma simulação mais demorada e menos precisa quando próximo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} .
Combinando as duas equações vistas, podemos escrever que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau \sim \xi^z} . Essa relação indica que o tempo de correlação aumenta com o tamanho típico dos clusters. Considerando um sistema de tamanho finito porém (os tipos de sistema que simulamos), o valor máximo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} vai ser o tamanho Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} do sistema (e.g. um sistema Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 64} xFalhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 64} tem Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L=64} ). Podemos assim concluir que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau \sim L^z} .
Sabendo a temperatura crítica do sistema (para Ising 2D, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c = 2.269J} é possível usar a relação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau \sim L^z} para medir Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} por meio de simulações onde a temperatura do sistema é igual à temperatura crítica para vários tamanhos diferentes de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} , plotando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} versus Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} em escala logarítmica. A inclinação da reta que liga todos esses pontos nos dá o valor de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} .
Por meio desse método, temos que o Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} do algoritmo de Metropolis é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = 2.1655 \pm 0.0012} e o Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} do algoritmo de Wolff (um algoritmo de clusterização) é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = 0.25 \pm 0.001} .
O motivo do tempo grande do algoritmo de Metropolis é a divergência do tamanho de correlação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi} próximo da temperatura crítica. Ao se aproximar de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} , grandes regiões se formam onde todos os spins estão alinhados, e é demorado para que o algoritmo flipe essas regiões, dado que ele flipa os spins sítio por sítio.
Algoritmos de cluster, como o de Wolff, fazem uso da técnica de clusterização. Com isso, os algoritmos encontram agrupam spins alinhados em clusters que apontam para a mesma direção e flipam os spins desse cluster ao mesmo tempo. Algoritmos de clusterização permitem uma exploração mais efetivo do espaço de fase próximo da temperatura crítica por serem mais eficientes e de precisarem de menos iterações para terem medidas precisas.
Balanço Detalhado
Para respeitarmos o Balanço Detalhado, precisamos que a mudança da rede de um estado $Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} para um estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} ocorra com a mesma probabilidade da mudança de um estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} , denotamos essa mudança por: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(\mu \to \nu) = A(\nu \to \mu)} , com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x \to y)} sendo a razão de aceitação da mudança de um estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} para um estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} .
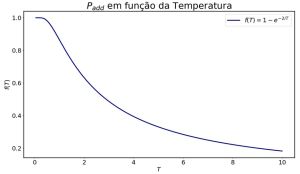
Supondo que estamos mudando de um estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} para outro estado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} , temos que a diferença de energia entre esses dois é resultado da quebra das ligações entre pares de spins orientados na mesma direção que não foram adicionados ao cluster, já que, não há uma garantia que a ida de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu \to \mu } quebre a mesma quantidade de ligações que a volta de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu \to \nu} . A probabilidade de não adicionarmos um spin vizinho ao cluster é dada por: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 - P_{add}} ; uma vez que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{add}} é a probabilidade de incluir esse spin no cluster.
Supondo que existam Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} ligações a serem quebradas na ida de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu \to \mu} , a probabilidade desse evento é dada por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1-P_{add})^m} . Porém, o mesmo pode não valer para a volta de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu \to \nu} , em razão disso, precisamos analisar o caso em que não há o mesmo número de ligações a serem quebradas na volta e então a probabilidade será dada por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1-P_{add})^n} com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} sendo o número de ligações a serem quebradas de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu \to \nu} .
Consideramos agora que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\nu}} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\mu}} sejam as energias associadas aos estados Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu } , respectivamente, temos que: a cada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} ligações que são quebradas de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu \to \nu} a energia aumenta com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle +2J} e para cada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} novas ligações geradas de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu \to \nu} a energia diminui com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2J} . Pode-se escrever então que a diferença de energia entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} é dada por: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\nu} - E_{\mu} = 2mJ -2nJ = 2J(m-n)}
Seguindo a definição do Balanço Detalhado e impondo que o Processo Markoviano dessas mudanças de estados descritas acima respeite a Distribuição de Boltzmann, precisamos que: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{(1-P_{add})^m A(\mu \to \nu)}{(1-P_{add})^n A(\nu \to \mu) } = e^{-\beta(E_{\nu} - E_{\mu})} = (1-P_{add})^{m-n}\frac{A(\mu \to \nu)}{A(\nu \to \mu)}} , tal que, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{A(\mu \to \nu)}{A(\nu \to \mu)} = \big[e^{2\beta J}(1-P_{add})\big]^{n-m}\;\;\;\; \Longrightarrow P_{add} = 1-e^{-2\beta J} \Longrightarrow \frac{(1-P_{add})^m A(\mu \to \nu)}{(1-P_{add})^n A(\nu \to \mu) }=1 }
Algoritmo de Wolf
Dinâmica do Algoritmo
O algoritmo de Wolff baseia-se principalmente em 4 passos. são estes:
- 1 - Escolhe-se um sítio aleatório da rede;
- 2 - Entre seus 4 vizinhos, se o spin do vizinho for igual ao do sítio inicial, adicionamos o vizinho ao cluster com probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{add} = 1-e^{2\beta J}}
- 3 - Para cada vizinho que foi adicionado ao cluster no passo anterior, repetimos o processo do passo 2 adicionando os vizinhos desse vizinho que possuem spin na mesma direção com a mesma probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{add}} . Faz-se isso para todos os sítios que são adicionados ao cluster.
- 4 - Quando todos os vizinhos de todos os sítios adicionados ao cluster tiveram ao menos uma “chance” de serem adicionados ao cluster, flipamos o cluster.
Simulações
Animações
Obs: Nossos gifs ficaram com mais de 2mb, limite da wiki, estamos refazendo...
Propriedades do Algoritmo de Wolff
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{add}\;= \;1 - e^{-2\beta J} }
Códigos Fonte
Função da Dinâmica de Clusterização
def cluster_din(sitio):
stack = []
oldspin = s[sitio]
newspin = (-1)*s[sitio]
s[sitio] = newspin
sp=1
stack.append(sitio)
while (sp):
sp = sp-1
atual = stack[sp]
stack.pop()
for j in range(4):
nn=viz[atual][j]
if s[nn] == oldspin: #IF da orientação do vizinho
rfloat1 = rng.random()
if (rfloat1<prob) : #IF da inclusão no cluster
stack.append(nn)
sp = sp+1
s[nn] = newspin
return