Clusterização: mudanças entre as edições
| Linha 18: | Linha 18: | ||
=== Dinâmica do Algoritmo === | === Dinâmica do Algoritmo === | ||
O algoritmo de Wolff baseia-se principalmente em 4 passos. são estes: | |||
*'''1 - ''' Escolhe-se um sítio aleatório da rede; | |||
*'''2 - '''Entre seus 4 vizinhos, se o spin do vizinho for igual ao do sítio inicial, adicionamos o vizinho ao cluster com probabilidade <math> P_{add} = 1-e^{2\beta J}</math> | |||
*'''3 - ''' Para cada vizinho que foi adicionado ao cluster no passo anterior, repetimos o processo do passo '''2''' adicionando os vizinhos desse vizinho que possuem spin na mesma direção com a mesma probabilidade <math>P_{add}</math>. Faz-se isso para todos os sítios que são adicionados ao cluster. | |||
*'''4 - ''' Quando todos os vizinhos de todos os sítios adicionados ao cluster tiveram ao menos uma “chance” de serem adicionados ao cluster, ''flipamos'' o cluster. | |||
{| class="wikitable" style="text-align: center;" | {| class="wikitable" style="text-align: center;" | ||
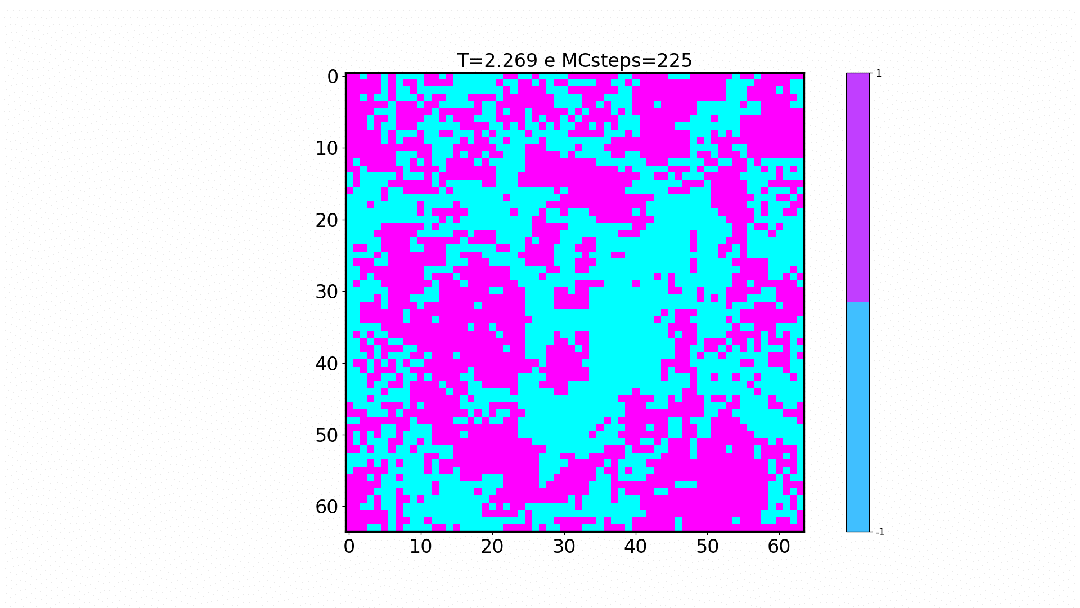
!colspan="2"|Dinâmica do algoritmo. | !colspan="2"|Dinâmica do algoritmo. | ||
Edição das 11h13min de 28 de maio de 2021
PÁGINA EM CONSTRUÇÃO
Clusterização do Modelo de Ising
Clusterização
Balanço Detalhado
Para respeitarmos o Balanço Detalhado, precisamos que a mudança da rede de um estado $ para um estado ocorra com a mesma probabilidade da mudança de um estado para , denotamos essa mudança por: , com sendo a razão de aceitação da mudança de um estado para um estado .
Supondo que estamos mudando de um estado para outro estado , temos que a diferença de energia entre esses dois é resultado da quebra das ligações entre pares de spins orientados na mesma direção que não foram adicionados ao cluster, já que, não há uma garantia que a ida de quebre a mesma quantidade de ligações que a volta de . A probabilidade de não adicionarmos um spin vizinho ao cluster é dada por: ; uma vez que é a probabilidade de incluir esse spin no cluster.
Supondo que existam ligações a serem quebradas na ida de , a probabilidade desse evento é dada por . Porém, o mesmo pode não valer para a volta de , em razão disso, precisamos analisar o caso em que não há o mesmo número de ligações a serem quebradas na volta e então a probabilidade será dada por com sendo o número de ligações a serem quebradas de .
Consideramos agora que e sejam as energias associadas aos estados e , respectivamente, temos que: a cada ligações que são quebradas de a energia aumenta com e para cada novas ligações geradas de a energia diminui com . Pode-se escrever então que a diferença de energia entre e é dada por:
Seguindo a definição do Balanço Detalhado e impondo que o Processo Markoviano dessas mudanças de estados descritas acima respeite a Distribuição de Boltzmann, precisamos que: , tal que,
Algoritmo de Wolf
Dinâmica do Algoritmo
O algoritmo de Wolff baseia-se principalmente em 4 passos. são estes:
- 1 - Escolhe-se um sítio aleatório da rede;
- 2 - Entre seus 4 vizinhos, se o spin do vizinho for igual ao do sítio inicial, adicionamos o vizinho ao cluster com probabilidade
- 3 - Para cada vizinho que foi adicionado ao cluster no passo anterior, repetimos o processo do passo 2 adicionando os vizinhos desse vizinho que possuem spin na mesma direção com a mesma probabilidade . Faz-se isso para todos os sítios que são adicionados ao cluster.
- 4 - Quando todos os vizinhos de todos os sítios adicionados ao cluster tiveram ao menos uma “chance” de serem adicionados ao cluster, flipamos o cluster.
| Dinâmica do algoritmo. | |
|---|---|




















![{\displaystyle {\frac {A(\mu \to \nu )}{A(\nu \to \mu )}}={\big [}e^{2\beta J}(1-P_{add}){\big ]}^{n-m}\;\;\;\;\Longrightarrow P_{add}=1-e^{-2\beta J}\Longrightarrow {\frac {(1-P_{add})^{m}A(\mu \to \nu )}{(1-P_{add})^{n}A(\nu \to \mu )}}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dc7dd4e75a96a1458cc3ccebcb3c98a06bc3d7e)