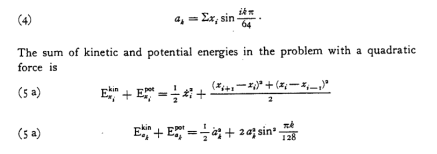Problema de Fermi-Pasta-Ulam: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 44: | Linha 44: | ||
</li> | </li> | ||
</ul></div></center> | </ul></div></center> | ||
== Resultados == | == Resultados == | ||
NOSSO GIF DEU MAIS DE 7 MEGA | |||
[[Arquivo:Estado inicial das particulas.png|center|thumb|500px|legenda.]] | |||
'''negrito''', ''Simultaneous OverRelaxation'' | '''negrito''', ''Simultaneous OverRelaxation'' | ||
| Linha 82: | Linha 59: | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
<center><div><ul> | <center><div><ul> | ||
<li style="display: inline-block;"> [[Arquivo: | <li style="display: inline-block;"> [[Arquivo:Estado inicial das particulas.png|center|thumb|500px|legenda.]] </li> | ||
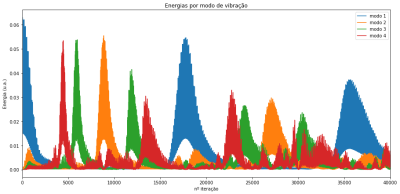
<li style="display: inline-block;"> [[Arquivo: | <li style="display: inline-block;"> [[Arquivo:Energias vibracao2.png|thumb|right|400px|legenda.]] </li> | ||
</ul></div></center> | </ul></div></center> | ||
== Discussões == | |||
Como o intuito era replicar os resultados através da simulação com dinâmica molecular obtivemos resultados muito parecidos comparando estudos já realizados sobre este problema ('''Citar estes artigos''') | |||
== Implementação == | |||
Usamos XX partículas, com modo de oscilação YY | |||
<source lang="haskell" line='line'> | |||
### Exemplo da iteração do movimento utilizando forcacom correção quadrática ### | |||
### código em python | |||
def aceleracao(pos,alpha,k,massa): | |||
size = len(pos) | |||
acel = [0.0 for i in range(size)] | |||
for i in range(1,size-1): | |||
acel[i] = (k/massa) * ((pos[i+1] + pos[i-1] - 2*pos[i]) * ( 1.0 + alpha*(pos[i+1]-pos[i-1]) ) ) | |||
return acel | |||
def velocidade(velo, acel, dt): | |||
size = len(velo) | |||
new_velo = [0.0 for i in range(size)] | |||
for i in range(size): | |||
new_velo[i] = velo[i] + 0.5*acel[i]*dt | |||
return new_velo | |||
[[ | def posicao(pos, velo, dt): | ||
size = len(posY) | |||
new_posY = [0.0 for i in range(size)] | |||
for i in range(size): | |||
new_posY[i] = posY[i] + new_veloY[i]*dt | |||
return new_posY | |||
N = número de partículas | |||
dt = 0.2 | |||
x = np.linspace(0, x_final, dt) | |||
pos = np.sin( 2*x*pi / (N*dt)) | |||
< | while t < tmax: # Loop temporal | ||
plt.scatter(x,pos) # plotagem dos gráficos | |||
acel = aceleracao(pos_old,alpha,k,massa) | |||
velo = velocidade(veloY, new_aceY,dt) | |||
pos = posicao(posY_old, veloY, dt) | |||
pos_old = pos.copy() #sem ".copy()" o python usa o mesmo endereço de memória para 2 variáveis | |||
t = t + td | |||
gera_gif() | |||
</source> | |||
'''Falar um pouco mais da implementação?''' | |||
== Link para Códigos == | == Link para Códigos == | ||
Edição das 00h32min de 26 de maio de 2021
Grupo: Augusto M Giani e Henrique Padovani
O objetivo deste trabalho é replicar os resultados do problema proposto por Fermi-Pasta-Ulam em 1953 [1] sobre sistemas dinâmicos não lineares. As análises serão sobre a solução dos modos de vibração comparados à solução analítica para poucas massas e também sobre a energia do sistema para os modos de oscilação, enquanto o sistema evolui no tempo.
O Problema
O Problema proposto constitui-se de simulações em uma rede de partículas ligadas entre si através de molas que obedecem a Lei de Hooke com uma correção não-linear quadrática ou cúbica [2]
A lei de forças que rege o comportamento deste sistema é:
.
Onde e a deformação a cada 2 massas acopladas (), é a constante elástica da mola, é um parâmetro de deformação arbitrário que controla a correção não linear quadrática e é o parâmetro que controla a correção cúbica. Importante ressaltar que se é possuir assumir um valor não nulo, real, é igual a zero no nosso sistema, ou vice-versa. Não estamos analisando correções quadráticas somadas com correções cúbicas neste trabalho.
Motivação: O que era esperado e o paradoxo XXX
(wiki) In 1966, Izrailev and Chirikov proposed that the system will thermalize, if a sufficient amount of initial energy is provided.[4] The idea here is that the non-linearity changes the dispersion relation, allowing resonant interactions to take place that will bleed energy from one mode to another. A review of such models can be found in Livi et al.[5] Yet, in 1970, Ford and Lunsford insist that mixing can be observed even with arbitrarily small initial energies.[6] There is a long and complex history of approaches to the problem, see Dauxois (2008) for a (partial) survey.[7]
Discretização
A discretização deste problema gira em torno de abrir a equação das forças, e com o termo de aceleração, iterar o movimento das partículas a partir disso [3]. Partimos do problema com correção quadrática, ou seja, . Partindo de:
,
subtituímos pelas variáveis discretas:
,
Chegamos em:
Em que é a aceleração da j-ésima partícula, com ela conseguimos integrar o movimento das partículas.
[TEM QUE ESCREVER AQUI] A Energia do sistema pode ser calculada para cada oscilação, porém para obtermos algum resultado e comparar com o estudo de fermi pasta ulam, calculamos a energia dos primeiros modos de vibração da corda para demontrar o comportamento visívelmente períodico destas energias.
Resultados
NOSSO GIF DEU MAIS DE 7 MEGA
negrito, Simultaneous OverRelaxation
Discussões
Como o intuito era replicar os resultados através da simulação com dinâmica molecular obtivemos resultados muito parecidos comparando estudos já realizados sobre este problema (Citar estes artigos)
Implementação
Usamos XX partículas, com modo de oscilação YY
### Exemplo da iteração do movimento utilizando forcacom correção quadrática ###
### código em python
def aceleracao(pos,alpha,k,massa):
size = len(pos)
acel = [0.0 for i in range(size)]
for i in range(1,size-1):
acel[i] = (k/massa) * ((pos[i+1] + pos[i-1] - 2*pos[i]) * ( 1.0 + alpha*(pos[i+1]-pos[i-1]) ) )
return acel
def velocidade(velo, acel, dt):
size = len(velo)
new_velo = [0.0 for i in range(size)]
for i in range(size):
new_velo[i] = velo[i] + 0.5*acel[i]*dt
return new_velo
def posicao(pos, velo, dt):
size = len(posY)
new_posY = [0.0 for i in range(size)]
for i in range(size):
new_posY[i] = posY[i] + new_veloY[i]*dt
return new_posY
N = número de partículas
dt = 0.2
x = np.linspace(0, x_final, dt)
pos = np.sin( 2*x*pi / (N*dt))
while t < tmax: # Loop temporal
plt.scatter(x,pos) # plotagem dos gráficos
acel = aceleracao(pos_old,alpha,k,massa)
velo = velocidade(veloY, new_aceY,dt)
pos = posicao(posY_old, veloY, dt)
pos_old = pos.copy() #sem ".copy()" o python usa o mesmo endereço de memória para 2 variáveis
t = t + td
gera_gif()
Falar um pouco mais da implementação?
Link para Códigos
Fizemos no ambiente Colab em .ipynb, segue link do github:[1]
Referências
- ↑ ANDRADE, D. X.; ANJOS, P. H. R.; ASSIS, P. E. G.. Sobre a conexão entre alguns modelos físicos não-lineares. Rev. Bras. Ensino Fís., São Paulo , v. 39, n. 1, e1307, 2017 . Disponível em <http://www.scielo.br/scielo.php?script=sci_arttext&pid=S1806-11172017000100407&lng=pt&nrm=iso>. http://dx.doi.org/10.1590/1806-9126-rbef-2016-0083.
- ↑ http://www.physics.utah.edu/~detar/phys6720/handouts/fpu/FermiCollectedPapers1965.pdf - Fermi, Pasta, Ulam, Studies of non linear problems
- ↑ https://en.wikipedia.org/wiki/Fermi%E2%80%93Pasta%E2%80%93Ulam%E2%80%93Tsingou_problem










![{\displaystyle m{\ddot {x_{j}}}=k\left(x_{j+1}-2x_{j}+x_{j-1}\right)\left[1+\alpha \left(x_{j+1}-x_{j-1}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3059ec0ad9ff614c3283f6a55b74997ffd2a83de)