Simulação de Micélio de Fungo: mudanças entre as edições
| Linha 13: | Linha 13: | ||
A criação de novas hifas, em geral, ocorre ao longo do tempo através de dois processos principais: o primeiro, denominado de '''ramificação dicotômica''', consiste na ponta de uma hifa já existente se dividindo ao meio. O segundo processo é chamado de '''ramificação lateral''', no qual, como o nome sugere, formam-se novos ramos e hifas na lateral de uma hifa já existente, como pode ser visto na figura 2. | A criação de novas hifas, em geral, ocorre ao longo do tempo através de dois processos principais: o primeiro, denominado de '''ramificação dicotômica''', consiste na ponta de uma hifa já existente se dividindo ao meio. O segundo processo é chamado de '''ramificação lateral''', no qual, como o nome sugere, formam-se novos ramos e hifas na lateral de uma hifa já existente, como pode ser visto na figura 2. | ||
Tendo em vista o objetivo deste trabalho, é importante entender o porquê e quando as ramificações citadas acimas ocorrem, para que possamos programá-las em nosso modelo computacional. A ramificação, portanto, é atribuída ao acúmulo de partículas de nutrientes e materiais no ambiente, o que estimula a extensão das hifas dos fungos em sua direção. Dessa maneira, '''o crescimento e desenvolvimento dos fungos são altamente dependentes e influenciados pela disponibilidade de nutrientes e materiais no ambiente ao seu redor.''' | |||
== Mecanismos Gerais dos Modelos == | == Mecanismos Gerais dos Modelos == | ||
Edição das 02h35min de 22 de maio de 2021
Grupo: Arthur Dornelles, Bruno Zanette, Gabriel De David e Guilherme Hoss
O objetivo deste trabalho é modelar computacionalmente o desenvolvimento de micélios em fungos com base em mecanismos gerais pré-estabelecidos. O progresso e a complexidade dos modelos cresceram de maneira gradual ao longo do trabalho através de três modelos de crescimento diferentes. O trabalho foi inspirado - principalmente - nos dois primeiros capítulos do artigo de Steven Hopkins [1].
Motivação e Introdução aos Fungos
Fungos estão integrados em grande parte dos ecossistemas do planeta e cumprem importantes funções na manutenção e sobrevivência dos mesmos. De maneira geral, eles produzem enzimas que são responsáveis pela decomposição de matéria orgânica e - portanto - a reciclagem de diversos nutrientes do ambiente ao seu redor [2]. Em muitos casos, fungos formam fusões simbióticas com plantas ou algas e interagem de diferentes maneiras com diferentes organismos vivos. Neste trabalho, todavia, não faremos a análise dessas interações e focaremos no comportamento individual de crescimento de fungos.
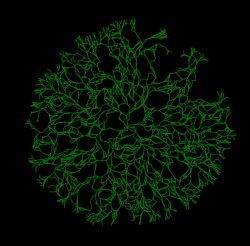
Anatomicamente, fungos são compostos por células que se assemelham a tubos microscópicos, denominadas de hifas. Essas hifas então se ramificam e se fundem umas com as outras em um processo chamado de anastomose, formando uma complexa rede chamada de micélio (figura 1).
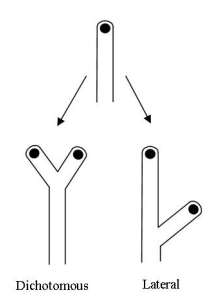
A criação de novas hifas, em geral, ocorre ao longo do tempo através de dois processos principais: o primeiro, denominado de ramificação dicotômica, consiste na ponta de uma hifa já existente se dividindo ao meio. O segundo processo é chamado de ramificação lateral, no qual, como o nome sugere, formam-se novos ramos e hifas na lateral de uma hifa já existente, como pode ser visto na figura 2.
Tendo em vista o objetivo deste trabalho, é importante entender o porquê e quando as ramificações citadas acimas ocorrem, para que possamos programá-las em nosso modelo computacional. A ramificação, portanto, é atribuída ao acúmulo de partículas de nutrientes e materiais no ambiente, o que estimula a extensão das hifas dos fungos em sua direção. Dessa maneira, o crescimento e desenvolvimento dos fungos são altamente dependentes e influenciados pela disponibilidade de nutrientes e materiais no ambiente ao seu redor.
Mecanismos Gerais dos Modelos
Crescimento
A distribuição de nutrientes ocorre de maneira discreta, não contínua.
Transporte de nutriente interno # Não será feito por exigir a computação de cada elemento individualmente toda vez
Fungo nº 1
- Branching na ponta
- Computar só os da ponta
- Crescimento ocorre só com o nutriente que o ponto final está
Fungo nº 2
- Branching lateral
- Morte (implementar idade da linha)
Fungo nº 3
- Junção (computação de cada elemento individualmente toda vez) (anastomosis)
Implementação
Crescimento
def crecimento (x,y):
theta= np.arctan(y/x)
if (x<0) :
theta= theta+ math.pi
aleatorio_theta = random.random()* math.pi/4 - math.pi/8 # angulo de -22.5 até 22.5 (45°)
theta=theta+aleatorio_theta
addx = r * math.cos(theta)
addy = r * math.sin(theta)
fx = x + addx
fy = y + addy
return (fx,fy)
Divisão
def divisao (x,y):
theta= np.arctan(y/x)
if (x<0) :
theta= theta+ math.pi
angulodivisao= random.random()*math.pi/2 #angulo para divisão de no máximo 90°
angulo1= theta- angulodivisao/2
angulo2= theta+ angulodivisao/2
addx1 = r * math.cos(angulo1)
addy1 = r * math.sin(angulo1)
addx2= r * math.cos(angulo2)
addy2= r * math.sin(angulo2)
Ax = x + addx1
Ay = y + addy1
Bx = x + addx2
By= y +addy2
return (Ax,Ay,Bx,By)
Intersecção de linhas: [3]
Referências
[1]HOPKINS, Steven. A Hybrid Mathematical Model of Fungal Mycelia: Tropisms, Polarised Growth and Application to Colony Competition, tese de doutorado, 2011.(https://core.ac.uk/download/pdf/6117416.pdf)
[2]DA SILVA, Priscila. Reino Fungi. InfoEscola (2018). Disponível em: https://www.infoescola.com/biologia/reino-fungi. Acesso em: 15 de Maio de 2021.
[3] Line to line intersection. Wikipédia. Disponível em: https://en.wikipedia.org/wiki/Line%E2%80%93line_intersection