Equação de Fitzhugh-Nagumo

Grupo: Bernardo Boatini, Murilo Kessler Azambuja e Natália Ferrazzo

O objetivo deste trabalho é implementar e estudar a dinâmica do modelo FitzHungh-Nagumo, e das equações que o compõem, para potenciais de ação em células e tecidos excitáveis. O método computacional utilizado para resolver os problemas e implementar o modelo foi o FTCS (Forward Time Centered Space) e o método de Crank-Nicolson.

Potencial de Ação em Neurônios

A células vivas são sistemas eletricamente sensíveis, ou seja, podem reagir a estímulos elétricos. Isso se dá devido ao fato de que substâncias carregadas estão naturalmente vinculadas a seus processos internos de interação com o ambiente, principalmente por intermédio de canais iônicos e proteínas transmebrana como, por exemplo, a Bomba de Sódio e Potássio(Bomba Na⁺/K⁺ ATPase)[1].

Naturalmente todas as células vivas possuem um potencial de repouso(PR) elétrico, ou seja, uma diferença de potencial elétrico, em relação ao meio(cerca de 0,1); mantida por um equilíbrio químico de concentração de íons dentro e fora da membrana plasmática.

Existem células que reagem estímulos elétricos apenas reestabelecendo o PR original por transporte passivo(sem gasto de energia) através da membrana, e estas são ditas células não-excitáveis.

Por outro lado, existem células que sob a ação do mesmo estímulo produzem um tipo de resposta bem característica: potencial de ação(PA); um pulso elétrico intenso(capaz de inverter a polarização do Potencial de Membrana) que se propaga ao longo da membrana da célula, sustentado por uma cadeia de transportes ativos(com gasto de energia) e que não decai ao longo do tempo e espaço; a esse tipo de células damos o nome de excitáveis[1].

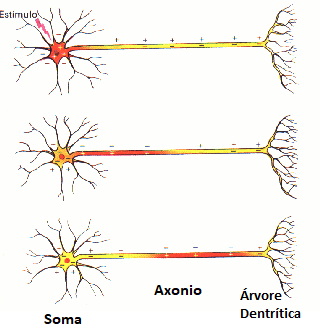
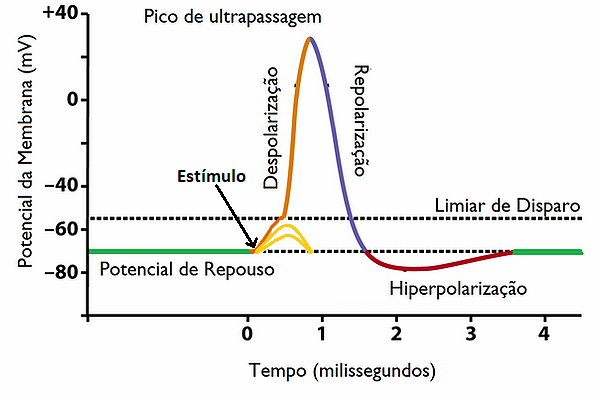
Os Neurônios são as células excitáveis do tecido nervoso(que constituem o encéfalo e medula espinhal, gânglios e nervos do reino animal) e com já vimos são capazes de gerar PA. Um potencial de ação pode assumir diversos formatos, mas ao longo do axônio(Figura 1) de um neurônio eles tendem a uma curva como a da Figura 2.

Figura 1 -Representação de um potencial de ação(vermelho) ao longo de um axônio de neurônio, partindo do soma neural em direção a arvore dentrítica.

Figura 2 -Curva de um Potencial de Ação genérico no tempo, em um ponto do axônio de um neurônio.

Olhando para Figura 2 vemos alguns aspectos importantes:

• O potencial de ação necessita de um estímulo mínimo(limiar) para ser ativado, abaixo desse valor o estímulo decai como em uma célula não excitável;
• Acima desse limiar a célula segue o principio de "Tudo ou Nada", ou seja, assume o valor máximo possivel dentro de sua capacidade, independente do estímulo aplicado;
• A etapa de despolarização(crescimento) é brusca e varia mais rapidamente que a repolarização(decaimento);
• O período que contém a repolarização e hiperpolarização da membrana é chamado período refratário, e se caracteriza por não permitir que ocorra nenhum disparo até que a membrana atinja o potencial de repouso.

Modelo

Equação de Nagumo

Para iniciar a modelagem do sistema, devemos antes enfatizar três condições básicas que o potencial deve obedecer para que seja um PA:

• Deve existir um limiar de voltagem para que um estímulo desencadeie o PA;
• Uma vez atingido o limiar, a voltagem deve aumentar até o máximo possível;
• Caso o estímulo não atinja o limiar, ele deve desaparecer rapidamente.

Podemos assim definir a variável normalizada que fará o papel de voltagem como $\upsilon$, sendo que $\upsilon =0$ é definido como o potencial de repouso, $\upsilon =1$ é o estímulo máximo e $\upsilon =\alpha$ é o limiar de voltagem. Desta forma podemos escrever as condições escritas acima como

Falhou ao verificar gramática (função desconhecida '\label'): {\displaystyle \begin{cases}\label(1) Se\ \upsilon>\alpha \Rightarrow \upsilon \rightarrow 1 \\ Se\ \upsilon<\alpha \Rightarrow \upsilon \rightarrow 0\\ \end{cases} }

Assim, a variação temporal do potencial elétrico na célula pode ser dada por

Falhou ao verificar gramática (função desconhecida '\del'): {\displaystyle \frac{\del \upsilon}{\del t} = f(\upsilon)}

Método de Crank-Nicolson

(explicar o método --> Natália)

Equação de Nagumo Difusiva 1D

(aplicar o método na equação e testar estabilidade --> Natália)

Método FTCS

(explicar o método --> Murilo)

Equação de Recuperação 1D

(aplicar o método na equação e testar estabilidade --> Murilo))

Modelo FitzHung-Nagumo 2D

(aplicar o método na equação e testar estabilidade --> Bernardo)

O sistema de EDP's em 2 dimensões é dado por, assumindo uma difusão isotrópica

${\frac {\partial v}{\partial t}}=D\left({\frac {\partial ^{2}v}{\partial x^{2}}}+{\frac {\partial ^{2}v}{\partial y^{2}}}\right)+f(v)-w$

${\frac {\partial w}{\partial t}}=\epsilon \left(v-\gamma w\right)$

Resultados

Equação de Nagumo Difusiva 1D

(explicar os testes e os gráficos/animações --> Natália)

Modelo FitzHung-Nagumo 1D

(explicar os testes e os gráficos/animações --> Murilo)

Modelo FitzHung-Nagumo 2D

(explicar os testes e os gráficos/animações --> Bernardo)

Discussão

(Contextualizar resultados --> Bernardo)

Referências

• 1. Jorge A. Quillfeldt,"ORIGEM DOS POTENCIAIS ELÉTRICOS DAS CÉLULAS NERVOSAS"
• 2. Eugene M. Izhikevich and Richard FitzHugh, "FitzHugh-Nagumo model"
• 3. Gabriel Perry Natanni Garcia, "NUMERICAL SIMULATION OF THE NAGUMO EQUATION BY FINITE DIFFERENCEMETHOD"
• 4. Binbin Xu, Stéphane Binczak, Sabir Jacquir, Oriol Pont, Hussein Yahia "Parameters Analysis of FitzHugh-Nagumo Model for a Reliable Simulation"