Mínimos Quadrados: mudanças entre as edições
(Criou página com 'Este o nome que se da ao ajuste ou ''fitting'' de uma função (polinômio) a um conjunto de dados. Se <math>(X_i, Y_i)</math> com <math>i=1, N</math> representam o conjunto de ...') |
Sem resumo de edição |
||
| Linha 1: | Linha 1: | ||
<!--- | |||
---> | |||
Este o nome que se da ao ajuste ou ''fitting'' de uma função (polinômio) a um conjunto de dados. | Este o nome que se da ao ajuste ou ''fitting'' de uma função (polinômio) a um conjunto de dados. | ||
Se <math>(X_i, Y_i)</math> com <math>i=1, N</math> representam o conjunto de dados (N) obtidos de um experimento (instrumento) ou | Se <math>(X_i, Y_i)</math> com <math>i=1, N</math> representam o conjunto de dados (N) obtidos de um experimento (instrumento) ou | ||
de uma observação (pesquisa de opinião ou censo) ou de uma simulação numérica. | de uma observação (por exemplo, em pesquisa de opinião ou censo) ou de uma simulação numérica. | ||
E se suspeitamos que existe uma correlação entre os X (variável independente ou de entrada, controlada pelo experimento) | E se suspeitamos que existe uma correlação entre os X (variável independente ou de entrada, controlada pelo experimento) | ||
e os Y (cuja dependência com X queremos testar), primeiro colocamos os pontos num gráfico para ver se o conjunto forma | e os Y (cuja dependência com X queremos testar), primeiro colocamos os pontos num gráfico para ver se o conjunto forma | ||
uma nuvem dispersa (quando não existe correlação aparente, isto é X e Y não conformam uma função), ou se existe | uma nuvem dispersa (quando não existe correlação aparente, isto é X e Y não conformam uma função), ou se existe | ||
correlação (os pontos parecem estar sobre alguma curva). <br> | correlação (os pontos parecem estar sobre alguma curva). <br> | ||
=Equação linear= | |||
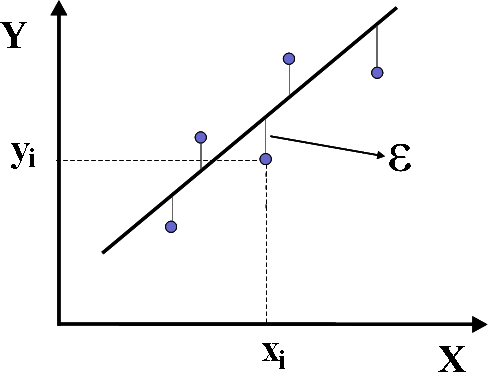
[[Image:minquadlinear.png|right|frame|Exemplo de ajuste linear para um conjunto de pontos.]] | |||
Sendo que um experimento foi realizado e temos <math>N</math> pontos, como descrito acima, e consideramos que um ajuste linear é coerente, uma reta deve ser construída para melhor representar estes pontos. Como mostrado na figura a baixo, para cada ponto, teremos um erro <math>\epsilon_i</math>, que é definido como a distância entre o ponto experimental e a curva (reta neste caso) teórica que desejamos ajustar, ou seja, | |||
:<math>\epsilon_i = Y_i - f(X_i)</math> , | |||
onde | |||
<!--- | |||
:<math>f(x) = \alpha_0 + \alpha_1x + \alpha_2x^2 + \alpha_3x^3 + .... + \alpha_nx^n</math> | |||
---> | |||
:<math>f(x) = \alpha_0 + \alpha_1x </math> | |||
é a função que representa a curva de melhor ajuste. | |||
Para encontrar a reta que melhor se ajusta aos dados experimentais, desejamos minimizar o erro <math>\epsilon</math>. Como o erro pode ter tanto valores negativos quanto positivos, o que importa é minimizar o valor absoluto de <math>\epsilon_i</math>. Isto poderia ser feito minimizando módulo de <math>\epsilon_i</math>, mas como a função módulo tem uma descontinuidade, é mais fácil minimizar o quadrado do erro. Para isto, definimos: | |||
:<math>S = \sum_{i=1}^N \epsilon_i^2</math>, | |||
assim | |||
:<math>S = \sum_{i=1}^N [Y_i - f(X_i)]^2 = \sum_{i=1}^N [Y_i - f(X_i;\alpha_0,\alpha_1)]^2 </math>. | |||
Para obter a melhor reta que se ajusta aos dados experimentais, temos que minimizar <math>S</math> em relação às constantes da função <math>(\alpha_0,\alpha_1)</math>: | |||
:<math>\frac{\partial S}{\partial \alpha_i} = 0</math>. | |||
Como a reta possui apenas dois coeficientes, para o ajuste linear temos duas equações: | |||
:<math>\frac{\partial S}{\partial \alpha_0} = \frac{\partial}{\partial \alpha_0}\sum_{i=1}^N [Y_i - (\alpha_0 + \alpha_1X_i)]^2 = 0</math> | |||
e | |||
:<math>\frac{\partial S}{\partial \alpha_1} = \frac{\partial}{\partial \alpha_1}\sum_{i=1}^N [Y_i - (\alpha_0 + \alpha_1X_i)]^2 = 0</math> . | |||
Derivando as equações acima, temos que | |||
:<math>\sum_{i=1}^N Y_i - \sum_{i=1}^N \alpha_0 - \sum_{i=1}^N \alpha_1X_i = 0</math> | |||
e | |||
:<math>\sum_{i=1}^N Y_iX_i - \sum_{i=1}^N \alpha_0X_i - \sum_{i=1}^N \alpha_1X_i^2 = 0</math> . | |||
Assim, | |||
:<math>\alpha_0\underbrace{\sum_{i=1}^N 1}_N + \alpha_1\underbrace{\sum_{i=1}^N X_i}_X = \underbrace{\sum_{i=1}^N Y_i}_Y </math> | |||
e | |||
:<math>\alpha_0\underbrace{\sum_{i=1}^N X_i}_X + \alpha_1\underbrace{\sum_{i=1}^N X_i^2}_{X^2} = \underbrace{\sum_{i=1}^N Y_iX_i}_{YX}</math> . | |||
Lembre-se de que os valores <math>X_i</math> e <math>Y_i</math> são conhecidos (são dados do problema). Desse modo, terminamos com um sistema linear para resolver, que na notação matricial fica | |||
:<math>\begin{pmatrix}N & X \\ X & X^2\end{pmatrix} \begin{pmatrix} \alpha_0 \\ \alpha_1 \end{pmatrix} = \begin{pmatrix} Y \\ YX \end{pmatrix}</math> . | |||
Cuidado com o fato que <math>(X^2 \neq X*X)</math> e <math>(YX \neq Y*X)</math>. Após construir a matriz, resolva com o método que mais lhe agrade (ha diversos métodos de solução de sistemas lineares, tais como a Regra de Cramer ou a eliminação Gaussiana). | |||
=Equação quadrática= | |||
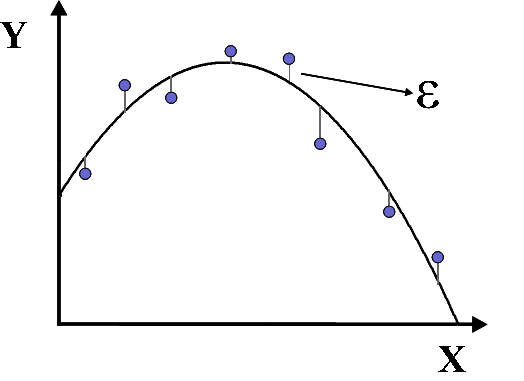
[[Image:minquadquadratico.png|right|frame|Exemplo de ajuste quadrático para um conjunto de pontos.]] | |||
Utilizando o mesmo método descrito para um ajuste linear, considerando que o melhor ajuste para um conjunto de pontos seja uma curva proveniente de função quadrática, temos que a função é dada por | |||
:<math>f(x) = \alpha_0 + \alpha_1x + \alpha_2x^2</math> . | |||
Desse modo, a soma do quadrado do erro fica | |||
:<math>S = \sum_{i=1}^N \epsilon_i^2 = \sum_{i=1}^N [Y_i - (\alpha_0 + \alpha_1X_i + \alpha_2X_i^2)]^2</math>. | |||
Após algumas contas, como feito na seção anterior, temos o sistema linear de 3 equações e 3 incógnitas para resolver: | |||
:<math>\begin{pmatrix} N & X & X^2 \\ X & X^2 & X^3 \\ X^2 & X^3 & X^4 \end{pmatrix} \begin{pmatrix} \alpha_0 \\ \alpha_1 \\ \alpha_2 \end{pmatrix} = \begin{pmatrix} Y \\ YX \\ YX^2 \end{pmatrix} </math> . | |||
Fique atento ao fato de que | |||
:<math>X = \sum_{i=1}^N X_i\, , \, Y = \sum_{i=1}^N Y_i \, , \, X^2 = \sum_{i=1}^N X_i^2 \, , \, X^3 = \sum_{i=1}^N X_i^3 \, , \, X^4 = \sum_{i=1}^N X_i^4 \, , \, YX = \sum_{i=1}^N Y_iX_i \,\, e \,\, YX^2 = \sum_{i=1}^N Y_iX_i^2</math> . | |||
=Polinômio de grau n= | |||
Generalizando o procedimento acima, apresentado para polinômios de grau 1 e 2, podemos ajustar um conjunto de pontos com um polinômio de um grau específico <math>n</math>. Assim, a função será descrita por | |||
<math>\ | :<math>f(x) = \alpha_0 + \alpha_1x + \alpha_2x^2 + \alpha_3x^3 + ... + \alpha_nx^n</math> | ||
e a soma dos quadrados do erro é dada por | |||
<math>\sum_{i=1}^N 2 | :<math>S = \sum_{i=1}^N \epsilon_i^2 = \sum_{i=1}^N [Y_i - f(X_i;\alpha_0,\alpha_1,...,\alpha_n)]^2</math>. | ||
<math>\ | Ao final do procedimento, teremos um sistema linear de <math>n</math> equações e <math>n</math> incógnitas para resolver. O resultado deste sistema são os coeficientes :<math>\alpha_0, \alpha_1, \alpha_2.. \alpha_n</math> que compõem o polinômio que melhor se ajusta aos dados experimentais. | ||
:<math>\begin{pmatrix}N & X & X^2 & \dots & X^n \\ X & X^2 & X^3 & \dots & X^{n+1} \\ X^2 & X^3 & X^4 & \dots & X^{n+2} \\ \vdots & \vdots & \vdots & \, & \vdots \\ X^n & X^{n+1} & X^{n+2} & \dots & X^{2n}\end{pmatrix} \begin{pmatrix} \alpha_0 \\ \alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_n \end{pmatrix} = \begin{pmatrix} Y \\ YX \\ YX^2 \\ \vdots \\ YX^n \end{pmatrix}</math> | |||
=Outros tipos de funções= | |||
Dependendo do tipo de experimento, podem haver outras relações entre os pontos, como funções exponenciais. | |||
==Exponencial 1== | |||
Se os dados de um experimento se ajustarem bem a uma função exponencial do tipo: | |||
:<math>f(x) = \alpha_1 e^{-\alpha_2x} \, , \, \, \, \alpha_1\, , \, \alpha_2 > 0 </math> , | |||
definimos uma nova função : | |||
:<math>f_2(x) = \ln(f(x)) = \ln(\alpha_1 e^{-\alpha_2 x}) = \ln(\alpha_1) - \alpha_2 x</math>. | |||
Assim, recaímos no problema do ajuste linear recém visto: | |||
:<math>f_2(x) = c_1 + c_2x</math>, com <math> c_1 = \ln(\alpha_1) </math> e <math> c_2 = - \alpha_2</math>. | |||
==Exponencial 2== | |||
Se a função exponencial for do tipo: | |||
:<math>f(x) = \alpha_1 \alpha_2^x</math>, | |||
supondo <math>f(x)>0</math>, definimos: | |||
:<math>f_2(x) = \ln(f(x)) = \ln(\alpha_1) + x\ln(\alpha_2)</math>. | |||
Assim, como no caso anterior, voltamos para o problema de ajuste linear: | |||
:<math>f_2(x) = c_1 + c_2x</math>, | |||
com <math> c_1 = \ln(\alpha_1) </math> e <math> c_2=\ln(\alpha_2)</math>. | |||
==Algébrica== | |||
Se a função for do tipo: | |||
:<math>f(x) = \alpha_1 x^{\alpha_2}</math> , | |||
com <math>f(x)>0</math> e <math>x>0</math>, definimos: | |||
:<math>f_2(x) = \ln(f(x)) = \ln(\alpha_1) + \alpha_2\ln(x)</math>. | |||
e assim | |||
:<math>f_2(x) = c_1 + c_2\ln(x)</math> , | |||
onde <math>c_1 = \ln(\alpha_1)</math> e <math>c_2 = \alpha_2</math>. Note também que os valores de x devem ser transformados em <math>\ln(x)</math> para ajustar os pontos. | |||
---- | |||
=Código FORTRAN= | |||
A seguir vemos uma possível implementação do método em linguagem F90.<br> | |||
Observem a simplicidade do mesmo: | |||
<pre> | |||
! programa fortran para ajuste linear de conjunto de dados | |||
Implicit none | |||
Real :: xi,yi, x,y,xy,x2 | |||
Real :: det,a,b | |||
n = 0; x = 0; y = 0; xy = 0; x2 = 0 | |||
Do | |||
Read(*,*,end=100) xi,yi | |||
n = n + 1 ! soma do numero de pontosd | |||
x = x + xi; y = y + yi ! somatorio dos x e y | |||
x2 = x2 + xi**2; xy = xy + xi*y ! somatorio dos x**2 e x*y <- cuidado ha um erro aqui (compila mas ... | |||
End Do | |||
100 det = n*x2 - x**2 | |||
a = y*x2 - xy*x / det ! <- outro erro aqui | |||
b = ... / det ! fica como exercicio | |||
print*, 'a=', a, 'b=', b | |||
end | |||
</pre> | |||
=Ajuste ponderado= | |||
Dependendo da situação, convém fazer um ajuste levando em conta o erro associado a cada ponto, i.e., atribuindo maior peso para pontos com um erro baixo e menor peso para os pontos onde o erro é sabidamente maior.Ou seja, se definirmos <math>w_i</math> como o peso associado ao ponto <math>(X_i,Y_i)</math>, gostaríamos que ele seja maior quanto menor for o erro associado a este ponto. | |||
Se <math>S_{y_i}</math> é o erro associado a este ponto, e considerando que o ajuste proposto é tal que minimiza a distância quadrática, podemos definir então <math>w_i</math> como: | |||
<math>w_i=S_{y_i}^{-2}</math> | |||
E a variável <math>\chi</math>, para o cálculo do ajuste ponderado, será dada por: | |||
<math>\chi = \sum_{i=1}^N (Y_i - a - b X_i)^{2}w_i</math> | |||
Aplicando o mesmo procedimento anterior para minimizar <math> \chi </math>, obtemos as equações | |||
:<math> \begin{bmatrix} | :<math> \begin{bmatrix} | ||
a[ | a[w] + b[Xw] & = &[Yw] \\ | ||
a[ | a[Xw] + b[X^2w] & = & [XYw] | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
Ou seja, | E, portanto, os valores de <math>a</math> e <math>b</math> são: | ||
<math>\Delta = [w][X^2w] - [Xw]^2</math> | |||
<math>a = [Yw][X^2w] - [XYw][Xw] / \Delta</math> | |||
<math>b = [w][XYw] - [Xw][Yw] / \Delta</math> | |||
=Erro dos coeficientes= | |||
Vimos como obter os coeficientes (a e b para uma reta) do ajuste de um conjunto de dados.<br /> | |||
Também como fazer esse ajuste quando os erros na variável dependente y não são todos iguais.<br /> | |||
Mas como saber se esses coeficientes são "bons". Ou seja, que margem de erro eles tem.<br /> | |||
Intuitivamente sabemos que quanto maior seja a dispersão dos <math>y_i</math> em volta | |||
da curva do ajuste, maior será nossa incerteza sobre os coeficientes. | |||
Vamos ver como traduzir isso de forma quantitativa. Voltando as expressões dos coeficientes a e b, | |||
eles são funções de <math>x_i</math> e <math>y_i</math>, onde só os segundos são considerados como | |||
fonte de erro. Assim para ver como o erro neles propaga-se para os coeficientes, escrevemos: | |||
<math>a = a(y_i) \Rightarrow \frac{\partial a}{\partial y_i} = \frac{1}{\Delta} \frac{\partial }{\partial y_i} \left\{[Yw][X^2w] - [XYw][Xw]\right\}</math> | |||
<math>\frac{\partial a}{\partial y_i} = \frac{1}{\Delta}\left\{ w_i[X^2w] - x_i w_i [Xw]\right\}</math> | |||
pois só os termos com y contribuem para a derivada. e como os <math>y_i</math> aparecem somados, ao derivar respeito do i-esimo | |||
sobra apenas o que multiplica ele | |||
Para incluir o efeito do erro de cada y_i deveriamos somar i de 1 a N, mas como o erro pode ser para mais o menos | |||
fazemos uma media quadrática deles: | |||
<math>\Delta a = \sqrt{\sum_{i=1}^N \left( \frac{\partial a}{\partial y_i} \Delta y_i \right)^2}</math> | |||
onde: | |||
<math>\left(\frac{\partial a}{\partial y_i}\Delta y_i \right)^2 = \frac{1}{\Delta^2} \left\{ w_i^2[X^2w]^2 + x_i^2 w_i^2 [Xw]^2 - 2w_i[X^2w] x_i w_i [Xw]\right\}w_i^{-1}</math> | |||
o somatório fica: | |||
<math>\frac{1}{\Delta^2} \sum_{i=1}^N \left(w_i[X^2w]^2 + x_i^2 w_i [Xw]^2 - 2 [X^2w] x_i w_i [Xw]\right) = | |||
\frac{1}{\Delta^2} \left([w][X^2w]^2 + [X^2w][Xw]^2 - 2 [X^2w][Xw][Xw]\right)</math> | |||
e com mais algumas simplificações chegamos a simples relação: | |||
<math>\Delta a = \sqrt{\frac{[X^2w]}{\Delta}}</math> | |||
Analogamente para o b (que resulta ser mais fácil), se chega a: | |||
<math>\Delta b = \sqrt{\frac{[w]}{\Delta}}</math> | |||
Podemos interpretar essa expressões no caso sem ponderar, ou seja quando todos os erros são iguais: | |||
<math>w=1/(\Delta y)^2</math> | |||
:<math>\Rightarrow \Delta = w^2 (N[X^2] - [X]^2)= (w N \sigma)^2</math> | |||
onde <math>\sigma^2 = <x^2> - <x>^2</math> | |||
\ | |||
</math> | |||
resultando: | |||
<math> | <math>\Delta a = \Delta y \sqrt{\frac{<x^2>}{N\sigma^2}}</math> | ||
<math> | <math>\Delta b = \Delta y \sqrt{\frac{1}{N\sigma^2}}</math> | ||
Ou seja quanto maior o número e mais espalhadas no eixo X as medidas melhor | |||
Edição das 11h56min de 18 de outubro de 2011
Este o nome que se da ao ajuste ou fitting de uma função (polinômio) a um conjunto de dados.
Se com representam o conjunto de dados (N) obtidos de um experimento (instrumento) ou
de uma observação (por exemplo, em pesquisa de opinião ou censo) ou de uma simulação numérica.
E se suspeitamos que existe uma correlação entre os X (variável independente ou de entrada, controlada pelo experimento)
e os Y (cuja dependência com X queremos testar), primeiro colocamos os pontos num gráfico para ver se o conjunto forma
uma nuvem dispersa (quando não existe correlação aparente, isto é X e Y não conformam uma função), ou se existe
correlação (os pontos parecem estar sobre alguma curva).
Equação linear
Sendo que um experimento foi realizado e temos pontos, como descrito acima, e consideramos que um ajuste linear é coerente, uma reta deve ser construída para melhor representar estes pontos. Como mostrado na figura a baixo, para cada ponto, teremos um erro , que é definido como a distância entre o ponto experimental e a curva (reta neste caso) teórica que desejamos ajustar, ou seja,
- ,
onde
é a função que representa a curva de melhor ajuste.
Para encontrar a reta que melhor se ajusta aos dados experimentais, desejamos minimizar o erro . Como o erro pode ter tanto valores negativos quanto positivos, o que importa é minimizar o valor absoluto de . Isto poderia ser feito minimizando módulo de , mas como a função módulo tem uma descontinuidade, é mais fácil minimizar o quadrado do erro. Para isto, definimos:
- ,
assim
- .
Para obter a melhor reta que se ajusta aos dados experimentais, temos que minimizar em relação às constantes da função :
- .
Como a reta possui apenas dois coeficientes, para o ajuste linear temos duas equações:
e
- .
Derivando as equações acima, temos que
e
- .
Assim,
e
- .
Lembre-se de que os valores e são conhecidos (são dados do problema). Desse modo, terminamos com um sistema linear para resolver, que na notação matricial fica
- .
Cuidado com o fato que e . Após construir a matriz, resolva com o método que mais lhe agrade (ha diversos métodos de solução de sistemas lineares, tais como a Regra de Cramer ou a eliminação Gaussiana).
Equação quadrática
Utilizando o mesmo método descrito para um ajuste linear, considerando que o melhor ajuste para um conjunto de pontos seja uma curva proveniente de função quadrática, temos que a função é dada por
- .
Desse modo, a soma do quadrado do erro fica
- .
Após algumas contas, como feito na seção anterior, temos o sistema linear de 3 equações e 3 incógnitas para resolver:
- .
Fique atento ao fato de que
- .
Polinômio de grau n
Generalizando o procedimento acima, apresentado para polinômios de grau 1 e 2, podemos ajustar um conjunto de pontos com um polinômio de um grau específico . Assim, a função será descrita por
e a soma dos quadrados do erro é dada por
- .
Ao final do procedimento, teremos um sistema linear de equações e incógnitas para resolver. O resultado deste sistema são os coeficientes : que compõem o polinômio que melhor se ajusta aos dados experimentais.
Outros tipos de funções
Dependendo do tipo de experimento, podem haver outras relações entre os pontos, como funções exponenciais.
Exponencial 1
Se os dados de um experimento se ajustarem bem a uma função exponencial do tipo:
- ,
definimos uma nova função :
- .
Assim, recaímos no problema do ajuste linear recém visto:
- , com e .
Exponencial 2
Se a função exponencial for do tipo:
- ,
supondo , definimos:
- .
Assim, como no caso anterior, voltamos para o problema de ajuste linear:
- ,
com e .
Algébrica
Se a função for do tipo:
- ,
com e , definimos:
- .
e assim
- ,
onde e . Note também que os valores de x devem ser transformados em para ajustar os pontos.
Código FORTRAN
A seguir vemos uma possível implementação do método em linguagem F90.
Observem a simplicidade do mesmo:
! programa fortran para ajuste linear de conjunto de dados
Implicit none
Real :: xi,yi, x,y,xy,x2
Real :: det,a,b
n = 0; x = 0; y = 0; xy = 0; x2 = 0
Do
Read(*,*,end=100) xi,yi
n = n + 1 ! soma do numero de pontosd
x = x + xi; y = y + yi ! somatorio dos x e y
x2 = x2 + xi**2; xy = xy + xi*y ! somatorio dos x**2 e x*y <- cuidado ha um erro aqui (compila mas ...
End Do
100 det = n*x2 - x**2
a = y*x2 - xy*x / det ! <- outro erro aqui
b = ... / det ! fica como exercicio
print*, 'a=', a, 'b=', b
end
Ajuste ponderado
Dependendo da situação, convém fazer um ajuste levando em conta o erro associado a cada ponto, i.e., atribuindo maior peso para pontos com um erro baixo e menor peso para os pontos onde o erro é sabidamente maior.Ou seja, se definirmos como o peso associado ao ponto , gostaríamos que ele seja maior quanto menor for o erro associado a este ponto. Se é o erro associado a este ponto, e considerando que o ajuste proposto é tal que minimiza a distância quadrática, podemos definir então como:
E a variável , para o cálculo do ajuste ponderado, será dada por:
Aplicando o mesmo procedimento anterior para minimizar , obtemos as equações
E, portanto, os valores de e são:
Erro dos coeficientes
Vimos como obter os coeficientes (a e b para uma reta) do ajuste de um conjunto de dados.
Também como fazer esse ajuste quando os erros na variável dependente y não são todos iguais.
Mas como saber se esses coeficientes são "bons". Ou seja, que margem de erro eles tem.
Intuitivamente sabemos que quanto maior seja a dispersão dos em volta
da curva do ajuste, maior será nossa incerteza sobre os coeficientes.
Vamos ver como traduzir isso de forma quantitativa. Voltando as expressões dos coeficientes a e b, eles são funções de e , onde só os segundos são considerados como fonte de erro. Assim para ver como o erro neles propaga-se para os coeficientes, escrevemos:
pois só os termos com y contribuem para a derivada. e como os aparecem somados, ao derivar respeito do i-esimo sobra apenas o que multiplica ele
Para incluir o efeito do erro de cada y_i deveriamos somar i de 1 a N, mas como o erro pode ser para mais o menos fazemos uma media quadrática deles:
onde:
o somatório fica:
e com mais algumas simplificações chegamos a simples relação:
Analogamente para o b (que resulta ser mais fácil), se chega a:
Podemos interpretar essa expressões no caso sem ponderar, ou seja quando todos os erros são iguais:
onde
resultando:
Ou seja quanto maior o número e mais espalhadas no eixo X as medidas melhor








![{\displaystyle S=\sum _{i=1}^{N}[Y_{i}-f(X_{i})]^{2}=\sum _{i=1}^{N}[Y_{i}-f(X_{i};\alpha _{0},\alpha _{1})]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e33e340457504ce25871f12d59c4cbd8483d0b0)



![{\displaystyle {\frac {\partial S}{\partial \alpha _{0}}}={\frac {\partial }{\partial \alpha _{0}}}\sum _{i=1}^{N}[Y_{i}-(\alpha _{0}+\alpha _{1}X_{i})]^{2}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aeae7398e706bcc43c253fa911b740cfadbccdf)
![{\displaystyle {\frac {\partial S}{\partial \alpha _{1}}}={\frac {\partial }{\partial \alpha _{1}}}\sum _{i=1}^{N}[Y_{i}-(\alpha _{0}+\alpha _{1}X_{i})]^{2}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69936051de71788c3abd6e0f1de4aeb997d3c021)










![{\displaystyle S=\sum _{i=1}^{N}\epsilon _{i}^{2}=\sum _{i=1}^{N}[Y_{i}-(\alpha _{0}+\alpha _{1}X_{i}+\alpha _{2}X_{i}^{2})]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e02aef60d147a7470972e92366180c2e00d1358d)




![{\displaystyle S=\sum _{i=1}^{N}\epsilon _{i}^{2}=\sum _{i=1}^{N}[Y_{i}-f(X_{i};\alpha _{0},\alpha _{1},...,\alpha _{n})]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a0d65cee2817a4d962b85c81d8a40c178eb03f5)






















![{\displaystyle {\begin{bmatrix}a[w]+b[Xw]&=&[Yw]\\a[Xw]+b[X^{2}w]&=&[XYw]\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa92608bb1123a6801c44882996b0366b65aca46)


![{\displaystyle \Delta =[w][X^{2}w]-[Xw]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/804c17960bc224e5b13e1c9f18077892ba163ae6)
![{\displaystyle a=[Yw][X^{2}w]-[XYw][Xw]/\Delta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/49b6a732f9d02a1e675a98205112e61e3e2a50c1)
![{\displaystyle b=[w][XYw]-[Xw][Yw]/\Delta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa5d1645a58f4d56429147e8c4274a3d7426f10c)


![{\displaystyle a=a(y_{i})\Rightarrow {\frac {\partial a}{\partial y_{i}}}={\frac {1}{\Delta }}{\frac {\partial }{\partial y_{i}}}\left\{[Yw][X^{2}w]-[XYw][Xw]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c08683d7d84fb50428201d592ba02819b6530cb)
![{\displaystyle {\frac {\partial a}{\partial y_{i}}}={\frac {1}{\Delta }}\left\{w_{i}[X^{2}w]-x_{i}w_{i}[Xw]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c72bfb9bc62f5c5e07d8be159e8a399cb698728a)

![{\displaystyle \left({\frac {\partial a}{\partial y_{i}}}\Delta y_{i}\right)^{2}={\frac {1}{\Delta ^{2}}}\left\{w_{i}^{2}[X^{2}w]^{2}+x_{i}^{2}w_{i}^{2}[Xw]^{2}-2w_{i}[X^{2}w]x_{i}w_{i}[Xw]\right\}w_{i}^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43cc0307fd8d7b0d733f38916540fc5f546b9881)
![{\displaystyle {\frac {1}{\Delta ^{2}}}\sum _{i=1}^{N}\left(w_{i}[X^{2}w]^{2}+x_{i}^{2}w_{i}[Xw]^{2}-2[X^{2}w]x_{i}w_{i}[Xw]\right)={\frac {1}{\Delta ^{2}}}\left([w][X^{2}w]^{2}+[X^{2}w][Xw]^{2}-2[X^{2}w][Xw][Xw]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e04c4d34836141c43638fec41a7b8fed0e426ff)
![{\displaystyle \Delta a={\sqrt {\frac {[X^{2}w]}{\Delta }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59779bd0586bd4f67f895f40da5df8f72a0d989a)
![{\displaystyle \Delta b={\sqrt {\frac {[w]}{\Delta }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03aad5e8f06c46ad5345376b466216026aefdf31)

![{\displaystyle \Rightarrow \Delta =w^{2}(N[X^{2}]-[X]^{2})=(wN\sigma )^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5b1e69a1ebc35b078454703d23c0682112c36f2)


