Grupo2 - Ondas1: mudanças entre as edições
| Linha 176: | Linha 176: | ||
Pensando na condição inicial <math> u(x,0) = \sin{\Big(\frac{\pi x}{L}\Big)} </math>, e estendendo para além da corda (pensando no seno de <math> -\infty<x<\infty </math>), observamos que ela respeita as equações acima. | Pensando na condição inicial <math> u(x,0) = \sin{\Big(\frac{\pi x}{L}\Big)} </math>, e estendendo para além da corda (pensando no seno de <math> -\infty<x<\infty </math>), observamos que ela respeita as equações acima. | ||
== Análise de erros == | == Solução e Análise de erros == | ||
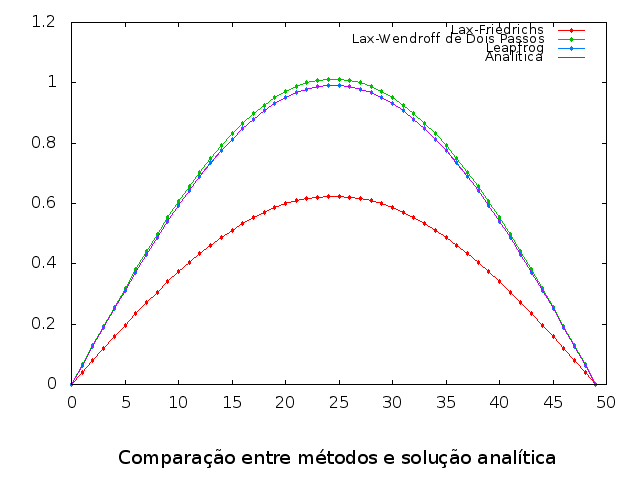
Primeiramente, | Primeiramente, apresentamos abaixo as soluções geradas pelos programas, em comparação com a solução analítica, e, em seguida, será mostrada a análise de erros. | ||
[[Arquivo:Output_comp.png|frame|100px|center|Comparação da solução analítica com as soluções numéricas]] | [[Arquivo:Output_comp.png|frame|100px|center|Comparação da solução analítica com as soluções numéricas]] | ||
Aqui já podemos observar o que foi comentado na seção sobre o método de Lax-Friedrichs: devido à dissipação numérica inerente ao método, há uma diminuição da amplitude da onda ao longo do tempo, embora ela mantenha sua forma. Isso interferirá na análise do erro deste método, o que será apresentado na sequência. | |||
A análise de erros se torna mais evidente durante a escolha do parâmetro <math>k</math>, onde <math>k = \frac{\Delta t}{\Delta x}</math>. Valores grandes trazem pouca acurácia, e valores pequenos necessitam de muito poder de computação (tempo e dinheiro). | A análise de erros se torna mais evidente durante a escolha do parâmetro <math>k</math>, onde <math>k = \frac{\Delta t}{\Delta x}</math>. Valores grandes trazem pouca acurácia, e valores pequenos necessitam de muito poder de computação (tempo e dinheiro). | ||
A partir do cálulo da solução analítica da equação da onda, podemos calcular quanto o valor obtido pelos métodos difere da solução real, o que leva a uma visualização do erro corrente em cada método de integração. | A partir do cálulo da solução analítica da equação da onda, podemos calcular quanto o valor obtido pelos métodos difere da solução real, o que leva a uma visualização do erro corrente em cada método de integração. | ||
Nesse caso, a solução é <math>u(x, t) = \cos{\Big(\frac{\pi t}{L}\Big)}\sin{\Big(\frac{\pi x}{L}\Big)}</math>. | Nesse caso, a solução é <math>u(x, t) = \cos{\Big(\frac{\pi t}{L}\Big)}\sin{\Big(\frac{\pi x}{L}\Big)}</math> <ref> | ||
Weisstein, Eric W. "Wave Equation--1-Dimensional." From MathWorld--A Wolfram Web Resource; disponível em: [http://mathworld.wolfram.com/WaveEquation1-Dimensional.html]; último acesso em 26/11/2017</ref>. | |||
O erro | O erro foi obtido efetuando uma média espacial, ou seja, o programa foi evoluindo até um tempo final <math>t_f = 100</math>, e, em <math>t=t_f</math>, foi feita uma média sobre o valor absoluto da diferença entre a solução analítica e a numérica. Aqui variamos o valor de <math>\Delta t</math>, fixando <math> \Delta x=1</math>, de forma que <math>k=\Delta t</math>. | ||
[[Arquivo:erro_dt.jpeg|frame|400px|center|Comparação do erro global entre os três métodos estudados com escala logarítimica em ambos os eixos]] | |||
Podemos observar | Podemos observar que os erros crescem à medida que o parâmetro k se torna maior, como seria de se esperar. | ||
Além disso, sabendo a ordem do erro dos métodos, podemos determinar a inclinação da reta que melhor se ajusta aos pontos. Se um método tem erro de ordem <math>(\Delta t)^n</math> | |||
<math>\varepsilon _l = \alpha (\Delta t)^n</math> | |||
em que <math>\varepsilon _l</math> é o erro local, ou seja, o erro de um passo do método, e <math>\alpha</math> é uma constante. Assim, o erro global <math>\varepsilon _g</math>, ou seja, o erro após N passos, é dado por | |||
<math>\varepsilon _g = N\varepsilon _l= N\alpha (\Delta t)^n </math> | |||
Como <math>N = \frac{t_f}{\Delta t}</math>, <math>\varepsilon _g = \frac{t_f}{\Delta t}\alpha (\Delta t)^n = \alpha t_f (\Delta t)^{n-1}</math> | |||
Logo, se o erro local é de ordem <math>(\Delta t)^n</math>, o erro global (que é o que calculamos aqui) é de ordem <math>(\Delta t)^{n-1}</math>. Além disso, como utilizamos escala logarítmica para representar os resultados, a função do erro global se torna | |||
<math>\log{\varepsilon _g} = \log{\alpha t_f (\Delta t)^{n-1}}</math> | |||
<math>\log{\varepsilon _g} = \log{\alpha t_f} + (n-1)\log{(\Delta t)}</math> | |||
Ou seja, a inclinação do gráfico do erro global é <math>n-1</math>. | |||
Observamos que se determinarmos a reta que melhor se ajusta às curvas dos métodos de Leapfrog e Lax-Wendroff, ela tem inclinação | Observamos que se determinarmos a reta que melhor se ajusta às curvas dos métodos de Leapfrog e Lax-Wendroff, ela tem inclinação aproximada de 1, já que os métodos são de ordem <math>(\Delta t)^2</math>. Com relação ao gráfico do erro do método de Lax-Friedrichs, é mais complicado de fazer sua análise, uma vez que há o efeito de dissipação numérica, que se intensifica para valores menores de <math>\Delta t</math>. Podemos observar nos dados que o ponto de máximo na parte esquerda do gráfico corresponde a um erro de aproximadamente <math>0,63</math>, que é a média da solução analítica no tempo <math>t = t_f</math> (conforme solução analítica, a amplitude no tempo <math>t=100</math> é <math>\cos{\Big(\frac{100\pi}{49}\Big)} \approx 1</math>, e a média de <math>\sin{\Big(\frac{\pi x}{L}\Big)}</math> vale <math>\frac{2}{\pi} \approx 0.64</math>). Isso significa que, devido à dissipação, a solução numérica é praticamente 0 frente à solução analítica na parte esquerda do gráfico. | ||
== Simulação de Propagação de Onda 2D no Mar Dependente de Topografia == | == Simulação de Propagação de Onda 2D no Mar Dependente de Topografia == | ||
Edição das 14h12min de 26 de novembro de 2017
Integrantes do grupo: Rodrigo Zamin Ferreira (262692), Leonardo Xavier Rodrigues (262696), Maurício Gomes de Queiroz (264889) e Rodrigo Lopes de Sousa Silva (262705)
Introdução
A modelagem numérica vem se tornando cada vez mais uma ferramenta indispensável para um engenheiro. Tal modelagem pode trazer informações importantes para entender como melhor abordar o desenvolvimento de um projeto, neste caso, um que envolva ondas. Nós, como futuros engenheiros físicos, pensamos em trazer um problema mais "concreto", de engenharia costeira e portuária, que pode ou não surgir em nossas vidas profissionais mas cujo método de solução certamente estará presente. Aqui será apresentado um modelo baseado em uma condição inicial e um perfil topográfico do local estudado que descreve a evolução temporal de uma onda.
Inicialmente, para testarmos os diferentes métodos, utilizaremos a equação da onda em uma dimensão, que é uma equação diferencial parcial de segunda ordem, para modelarmos uma corda:
em que é o deslocamento vertical da corda, é a velocidade de propagação da onda e , com o comprimento da corda.
Admitindo ,
.
Uma vez que os métodos citados abaixo são para equações de primeira ordem, é necessário separarmos a equação em um sistema de equações, fazendo a substituição e , de forma que:
As condições de contorno utilizadas aqui são (pontas fixas), e as condições iniciais são e
Algoritmos
Apresentaremos aqui três abordagens diferentes para a solução da equação diferencial parcial apresentada, e após, seus respectivos erros associados. A respeito das discretizações, corresponde à posição, e representa o tempo.
Método de Lax-Friedrichs -
Esse método consiste em inicialmente discretizar as equações no esquema FTCS (Forward Time Centered Space), ou seja, discretizando a derivada temporal utilizando os tempos n e n+1 e a derivada espacial através das posições j-1 e j+1:
,
.
Resultando em
,
.
Entretanto, ao se realizar uma análise de estabilidade de Von Neumann, conclui-se que esse método é instável[1] . Para torná-lo estável, é necessário trocarmos os termos e por suas médias espaciais, chegando, assim, na expressão do esquema de Lax-Friedrichs:
,
.
Para obtermos o valor de , que é o nosso objetivo, discretizamos a equação
,
Embora as médias espaciais sejam necessárias para a estabilidade do método, elas introduzem um problema: surge um efeito chamado de dissipação numérica, ou seja, a amplitude da solução diminui com o tempo. Isso pode ser observado através da análise de Von Neumann ou de uma investigação da equação do esquema Lax-Friedrichs [1] . Por este método, observa-se que ao inserirmos as médias, mudamos a equação original do problema, pois agora há também um termo do tipo difusivo (uma derivada segunda) [1].
Agora vamos unir todas as equações, utilizando, além da equação para obtida acima, as discretizações de e
,
.
Assim, obtemos
.
Método de Leapfrog -
Neste método utilizamos os pontos intermediários na discretização das equações.
Para temos
,
Para temos
,
Para temos
,
Utilizando o fato de que
,
,
chegamos na equação para
,
o que é equivalente a discretizarmos a equação da onda diretamente, utilizando que, para uma função ,
,
sendo a discretização em .
Método de Lax-Wendroff de Dois Passos -
O primeiro passo consiste em calcular o valor de e utilizando o método de Lax-Friedrichs, para posterior cálculo de e :
,
,
,
,
Agora, no tempo :
,
,
Agrupando as equações,
,
,
E finalmente temos a equação unificada em u, utilizando a expressão para e as discretizações de e , como obtidas na seção sobre o Método de Lax-Friedrichs:
,
Programas
Ao implementarmos o método, surgem dois problemas: o problema não é auto-inicializável, pois para calcularmos o valor de , necessitamos de (além de ). Entretanto, isto é rapidamente solucionado quando discretizamos a condição inicial de que :
,
ou seja, para o cálculo de , utilizamos que . Através do método de Leapfrog, dessa forma conseguimos isolar :
,
.
Porém, isso não ocorre com os outros dois métodos, pois surgem termos em diferentes posições para o tempo (de , , até ), sendo necessário resolvermos o sistema como um todo simultaneamente, ou seja, teríamos que inverter uma matriz. Por isso, foi utilizado o método de Leapfrog para o cálculo de em todos os métodos, devido a sua simplicidade.
Além disso, são necessários valores de e de , com correspondendo a , para calcularmos e , para qualquer tempo, utilizando os métodos de Lax-Wendroff de dois passos e Lax-Friedrichs. A solução a este problema foi utilizarmos
.
Pensando na condição inicial , e estendendo para além da corda (pensando no seno de ), observamos que ela respeita as equações acima.
Solução e Análise de erros
Primeiramente, apresentamos abaixo as soluções geradas pelos programas, em comparação com a solução analítica, e, em seguida, será mostrada a análise de erros.
Aqui já podemos observar o que foi comentado na seção sobre o método de Lax-Friedrichs: devido à dissipação numérica inerente ao método, há uma diminuição da amplitude da onda ao longo do tempo, embora ela mantenha sua forma. Isso interferirá na análise do erro deste método, o que será apresentado na sequência.
A análise de erros se torna mais evidente durante a escolha do parâmetro , onde . Valores grandes trazem pouca acurácia, e valores pequenos necessitam de muito poder de computação (tempo e dinheiro).
A partir do cálulo da solução analítica da equação da onda, podemos calcular quanto o valor obtido pelos métodos difere da solução real, o que leva a uma visualização do erro corrente em cada método de integração. Nesse caso, a solução é [2].
O erro foi obtido efetuando uma média espacial, ou seja, o programa foi evoluindo até um tempo final , e, em , foi feita uma média sobre o valor absoluto da diferença entre a solução analítica e a numérica. Aqui variamos o valor de , fixando , de forma que .
Podemos observar que os erros crescem à medida que o parâmetro k se torna maior, como seria de se esperar.
Além disso, sabendo a ordem do erro dos métodos, podemos determinar a inclinação da reta que melhor se ajusta aos pontos. Se um método tem erro de ordem
em que é o erro local, ou seja, o erro de um passo do método, e é uma constante. Assim, o erro global , ou seja, o erro após N passos, é dado por
Como , Logo, se o erro local é de ordem , o erro global (que é o que calculamos aqui) é de ordem . Além disso, como utilizamos escala logarítmica para representar os resultados, a função do erro global se torna
Ou seja, a inclinação do gráfico do erro global é .
Observamos que se determinarmos a reta que melhor se ajusta às curvas dos métodos de Leapfrog e Lax-Wendroff, ela tem inclinação aproximada de 1, já que os métodos são de ordem . Com relação ao gráfico do erro do método de Lax-Friedrichs, é mais complicado de fazer sua análise, uma vez que há o efeito de dissipação numérica, que se intensifica para valores menores de . Podemos observar nos dados que o ponto de máximo na parte esquerda do gráfico corresponde a um erro de aproximadamente , que é a média da solução analítica no tempo (conforme solução analítica, a amplitude no tempo é , e a média de vale ). Isso significa que, devido à dissipação, a solução numérica é praticamente 0 frente à solução analítica na parte esquerda do gráfico.
Simulação de Propagação de Onda 2D no Mar Dependente de Topografia
O modelo mais simples para a propagação de onda dependente da topografia parte da equação da onda [1], incluindo um termo da forma .
,
Sendo uma representação da profundidade em águas calmas. Em uma situação real, pode-se obtê-la por mapeamento eletrônico do terreno por sistema de sonar.
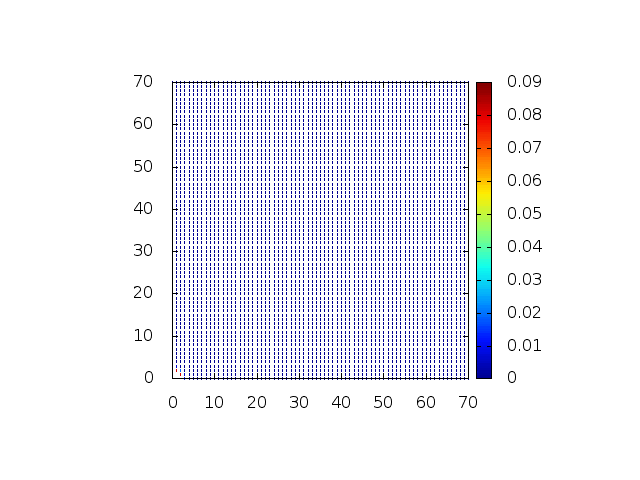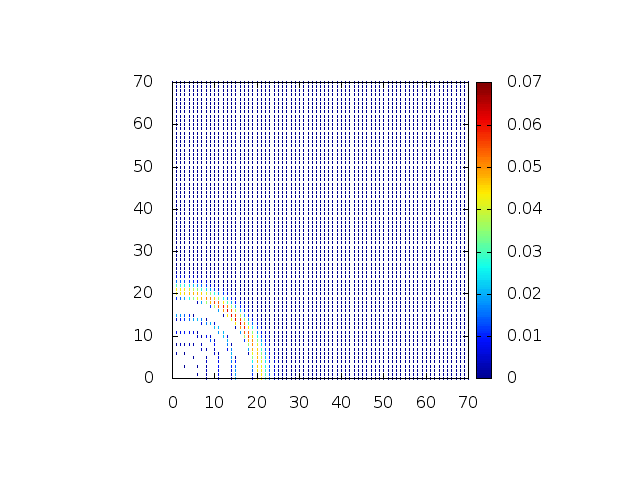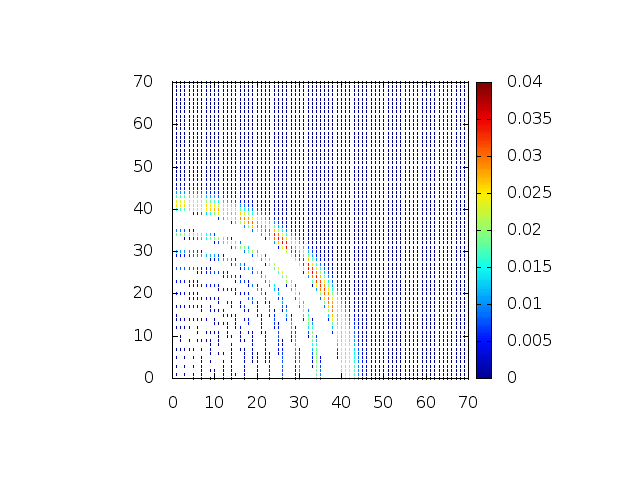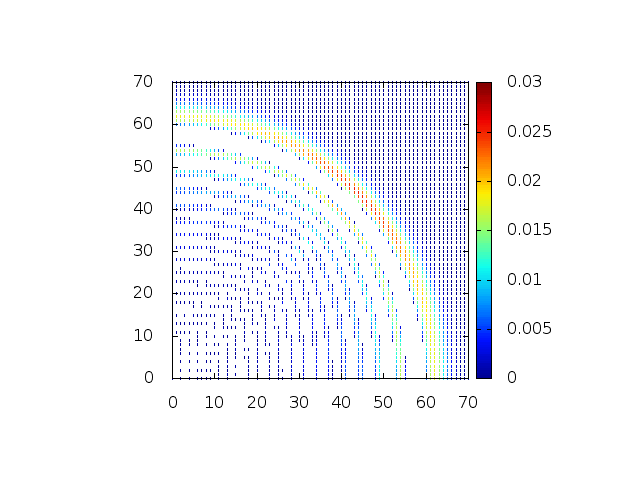
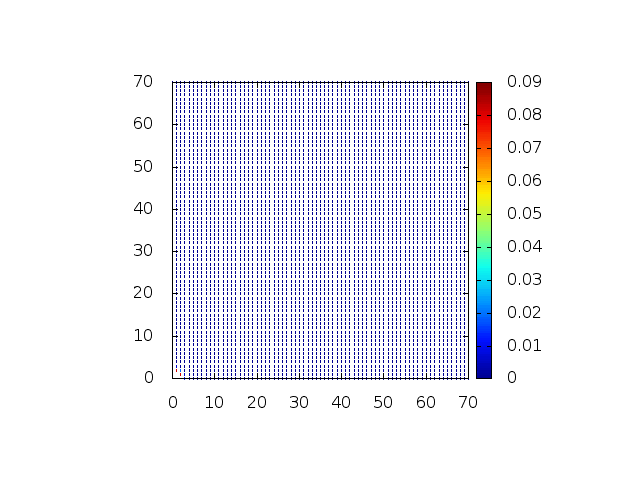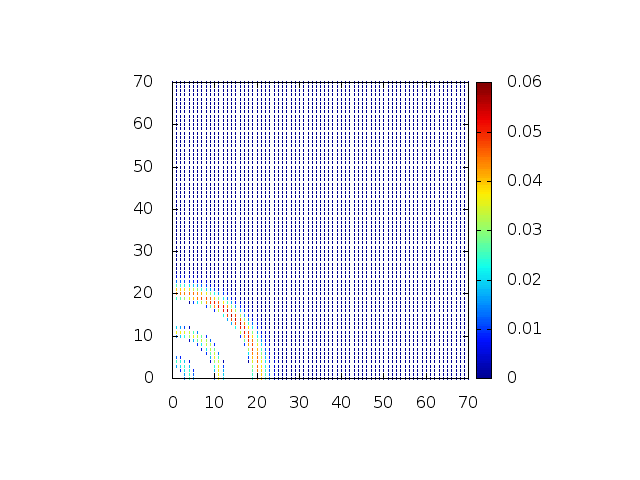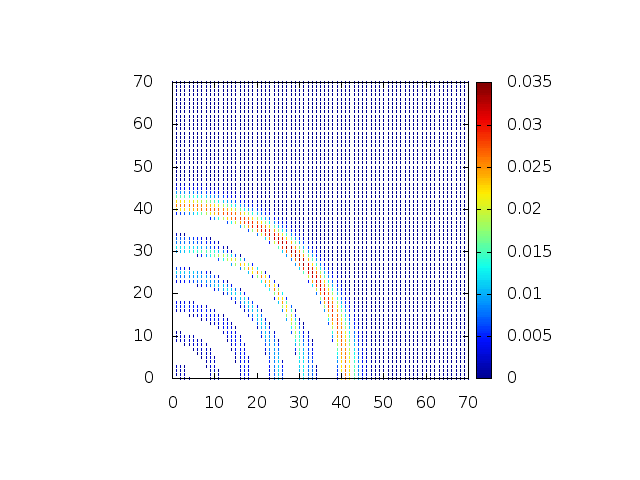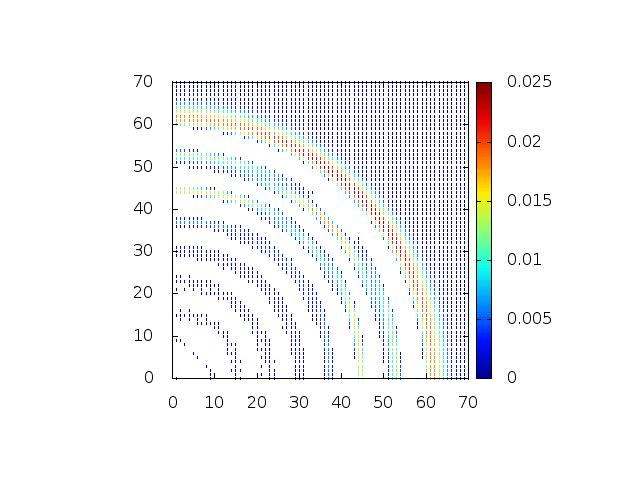
Como primeira abordagem visando uma análise em 2D, a integração da equação em 1D (mesmo sendo uma situação muito idealizada) já traz resultados interessantes. Podemos observar, por exemplo, que a medida que a profundidade diminui, a amplitude da onda e sua frequência crescem [5]. Esta informação por si só ajuda na construção de proteção contra quebra de ondas, pois é obtido o tamanho que as mesmas atingem.
É importante notar o quão poderosa é a integração de equações parciais na vida de um engenheiro.
A dependência em de permite um modelo no qual o terreno se modifica com o tempo. Isto é, pode-se observar o efeito que o deslocamento de placas tectônicas, deslizamentos, e até explosões provocam no comportamento das ondas na costa de um país e o reconhecimento de áreas críticas.
Estendendo o algoritmo do Leap-Frog à situação 2D, obtemos, para uma dada condição inicial e , onde é uma constante de valor igual a 1 e H não depende do tempo, por questão de simplicidade:
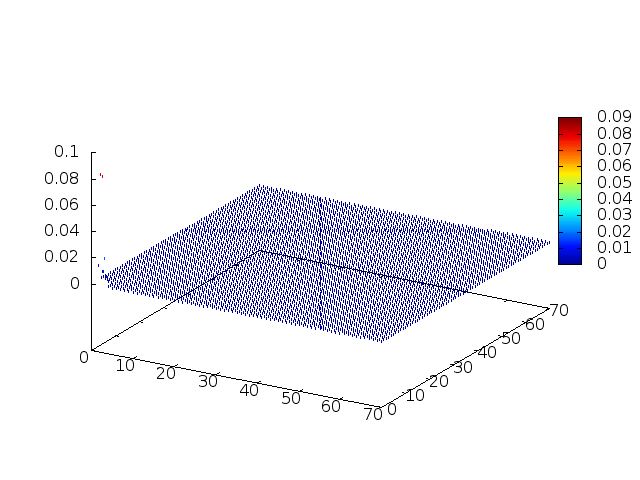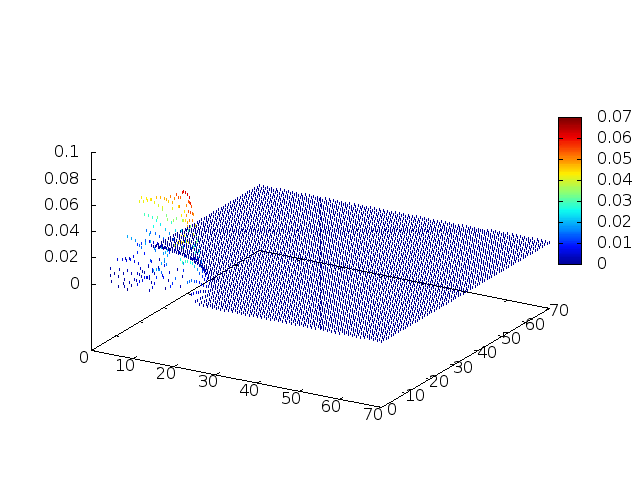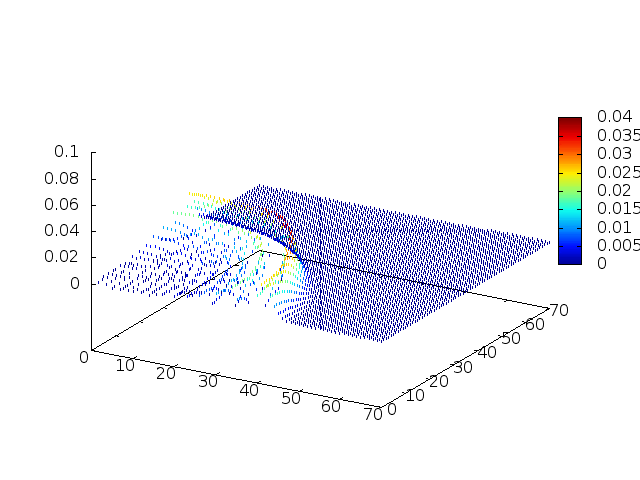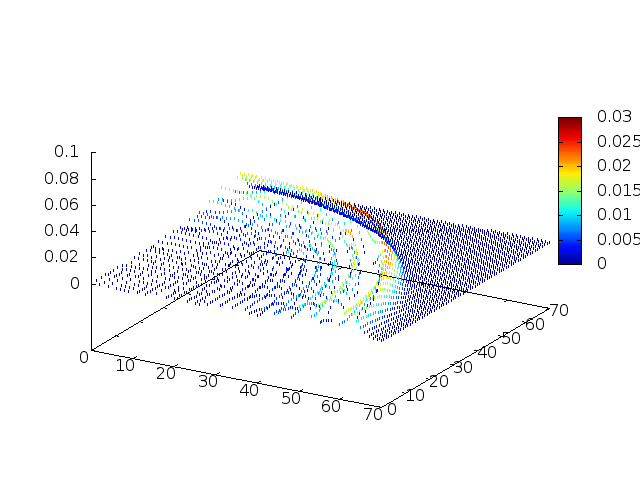
Podemos então, analisar como a mesma condição inicial se porta quando descreve uma gaussiana na origem:
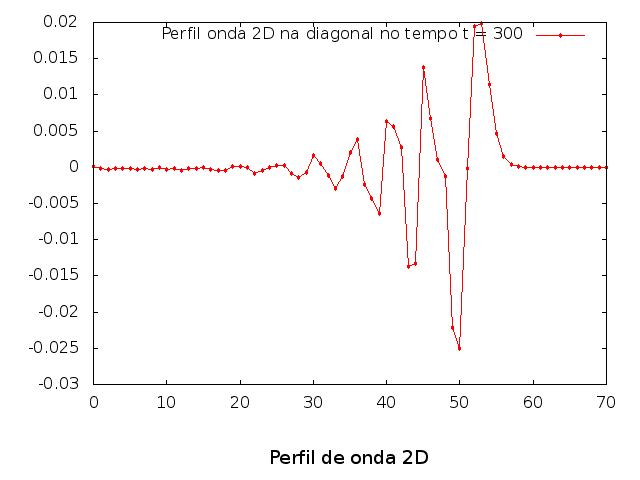
Perfil da onda em sua diagonal:
Bibliografia
- ↑ 1,0 1,1 1,2 Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007). Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8.
- ↑ Weisstein, Eric W. "Wave Equation--1-Dimensional." From MathWorld--A Wolfram Web Resource; disponível em: [1]; último acesso em 26/11/2017
1"The Wave Equation in 1D and 2D," por Knut–Andreas Lie, Dept. of Informatics, University of Oslo; disponível em: [2]; Último acesso em 23/10/2017.
2"Digital terrain mapping of the underside of sea ice from a small AUV," por Wadhams, M. J. Doble; disponível em: DOI: 10.1029/2007GL031921 ; Último acesso em 23/10/2017.
3 Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007). Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8.
4 "Métodos Computacionais da Física C - Aula 2 - 2016/1" por Heitor C. M. Fernandes, Instituto de Física, UFRGS; Último acesso em 23/10/2017.






















































![{\displaystyle w_{j}^{n+1}=w_{j}^{n}+{\frac {\Delta t}{\Delta x}}{\Bigg [}{\frac {1}{2}}(v_{j+1}^{n}-v_{j-1}^{n})+{\frac {\Delta t}{2\Delta x}}(w_{j+1}^{n}-2w_{j}^{n}+w_{j-1}^{n}){\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3a64c670bcee4e22ac06f0fd7bfff9e3f055588)
![{\displaystyle v_{j}^{n+1}=v_{j}^{n}+{\frac {\Delta t}{\Delta x}}{\Bigg [}{\frac {1}{2}}(w_{j+1}^{n}-w_{j-1}^{n})+{\frac {\Delta t}{2\Delta x}}(v_{j+1}^{n}-2v_{j}^{n}+v_{j-1}^{n}){\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f320f92413007a3cb3294078873ba6a1fada3e6)

![{\displaystyle u_{j}^{n+1}=2u_{j}^{n}-u_{j}^{n-1}+{\frac {(\Delta t)^{2}}{2(\Delta x)^{2}}}{\Bigg [}{\frac {1}{2}}u_{j+2}^{n-1}-{\frac {1}{2}}u_{j-2}^{n-1}+u_{j+1}^{n}-u_{j+1}^{n-1}-2u_{j}^{n}+u_{j}^{n-1}+u_{j-1}^{n}-u_{j-1}^{n-1}{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b5c239b890cdd05de6816d2444986009eb19f0f)