Equação de Ginzburg-Landau complexa

A equação de Ginzburg-Landau complexa (CGLE) é uma das equações não lineares mais estudadas da física. Ela oferece uma descrição geral de sistemas com uma fraca dependência não linear. Quando escrita de modo a minimizar o número de constantes, é dada pela equação abaixo:

${\frac {\partial A}{\partial t}}=(1+ic_{1})\nabla ^{2}A+A-(1-ic_{3})A|A|^{2}.$

Em especial, para $c_{1}=0$ e $c_{3}=0$, ela se reduz para a equação de Ginzburg-Landau real. E, para $c_{1}\rightarrow +\infty$ e $c_{3}\rightarrow +\infty$, ela se reduz à equação de Schrödinger não linear. Ela descreve uma variedade enorme de fenômenos, como:

• Ondas não lineares;
• Transições de fase de segunda ordem;
• Supercondutividade;
• Superfluidez;
• Condensado de Bose-Einstein.

Dedução

Figura 1 - Espaço de fase do oscilador harmônico. Fonte - Cross, M., & Greenside, H. (2009)

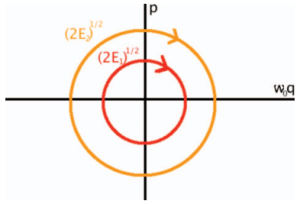
É possível deduzir a CGLE a partir do oscilador linear harmônico por meio de argumentos de simetria, encontrando a equação de Stuart-Landau, e, em seguida, considerando um sistema estendido no espaço. A energia de um oscilador harmônico é expressa pela equação abaixo, onde $E$ é a energia, $q$ e $p$ a coordenada e seu respectivo momento, $m$ é a massa e $\omega _{0}$ a frequência angular

$E={\frac {p^{2}}{2m}}+{\frac {1}{2}}m\omega _{0}^{2}q^{2}.$

Ao realizar as seguintes mudanças de variáveis, $q\rightarrow q/m^{1/2}$ e $p\rightarrow pm^{1/2}$, a equação da energia produz trajetórias circulares no espaço de fase de $\omega _{0}q$ e $p$

$E={\frac {p^{2}}{2}}+{\frac {1}{2}}\omega _{0}^{2}q^{2}.$

Essa é uma importante simetria do oscilador harmônico linear, resultando que a sua energia é proporcional ao quadrado da amplitude de oscilação, não dependendo da fase. Isso sugere uma motivação, qual é o menor termo não linear que pode ser adicionado de modo a preservar essa simetria. Para tanto, o estado do sistema será descrito em coordenadas polares, onde $R$ é a amplitude e $\phi$ a fase

${\dot {R}}=0,\quad {\dot {\phi }}=\omega _{0}.$

Define-se, então, a variável complexa $A=Re^{i\phi }$, portanto a equação acima pode ser reescrita como

${\dot {A}}=i\omega _{0}A.$

Ao realizar a transformação de variável $A\rightarrow Ae^{i\chi }$, com $\chi \in \mathbb {R}$, a equação acima permanece inalterada. Ou seja, a equação é invariante a rotações. Então, busca-se uma função não linear $f(A,A^{*})$ tal que

${\dot {A}}=i\omega _{0}A+f(A,A^{*})$

também seja invariante a rotações.

Então, perante às transformações $A\rightarrow Ae^{i\chi }$ e $A^{*}\rightarrow A^{*}e^{-i\chi }$, a função $f(A,A^{*})$ deve satisfazer

$f(Ae^{i\chi },A^{*}e^{-i\chi })=f(A,A^{*})e^{i\chi },$

para que seja possível fatorar o termo responsável pela rotação e obter novamente a equação original.

Considerando pequenas oscilações, é possível expandir $f(A,A^{*})$ em potências de $A$ e $A^{*}$ até a menor ordem possível que satisfaça a condição e que introduza uma não linearidade à equação. Com isso, obtém-se

$f(A,A^{*})=\alpha _{1}A+\alpha _{2}|A|^{2}A,\quad \alpha _{1}=\alpha _{1r}+i\alpha _{1i},\quad \alpha _{2}=\alpha _{2r}+i\alpha _{2i}$

Utilizando o resultado encontrado e expressando em coordenadas polares por meio de $A=Re^{i\phi }$

${\dot {R}}=\alpha _{1r}R+\alpha _{2r}R^{3},\quad {\dot {\phi }}=\omega _{0}+\alpha _{1i}+\alpha _{2i}R^{2}.$

Em seguida, muda-se para o referencial que gira com a mesma frequência do oscilador harmônico por meio da definição de $\phi =\varphi +\omega _{0}t$. As novas equações obtidas são

${\dot {R}}=\alpha _{1r}R+\alpha _{2r}R^{3},\quad {\dot {\varphi }}=\alpha _{1i}+\alpha _{2i}R^{2}.$

Para encontrar a amplitude estacionária, pode-se tomar ${\dot {R}}=0$ na equação, o que resulta na solução trivial $R^{(est)}=0$ e $R^{(est)}={\sqrt {-\alpha _{1r}/\alpha _{2r}}}$. Então, para que exista uma amplitude estacionária não nula, os sinais de $\alpha _{1r}$ e de $\alpha _{2r}$ devem ser opostos. Além disso, por inspeção observa-se que, caso $\alpha _{1r}<0$ e $\alpha _{2r}>0$, pequenos valores de amplitude irão diminuir e grandes valores de amplitude irão aumentar, o que indica que a solução estacionária não trivial será instável. Portanto, define-se $\alpha _{1r}=\mu \sigma _{1}$ para $\sigma _{1}>0$, $\alpha _{2i}=\mu \omega _{1}$, $\alpha _{2r}=-g_{r}$ com $g_{r}>0$ e $\alpha _{2i}=-g_{i}$. Por fim, ao voltar para a representação no plano complexo, chega-se em

${\dot {A}}=\mu (\sigma _{1}+\omega _{1})A-(g_{r}+ig_{i})|A|^{2}A$

Esta é a equação de Stuart-Landau. Para obter a equação complexa de Ginzburg-Landau, é necessário considerar um sistema espacialmente extenso, em que cada ponto é um oscilador modelado pela equação acima. Para isso, é adicionado um termo proporcional ao laplaciano de A, $(d_{r}+id_{i})\nabla ^{2}A$, cujo significado fica evidente ao discretizar a função. Ele computa a diferença de $A$ no sítio em questão com relação à média dos sítios vizinhos, resultando em uma tendência de pontos próximos oscilarem com amplitudes e fases semelhantes. Ao adicionar esse novo termo e redefinir as constantes de modo a reduzi-las sem perder as características importantes do sistema, chega-se na equação complexa de Ginzburg-Landau

${\frac {\partial A}{\partial t}}=(1+ic_{1})\nabla ^{2}A+A-(1-ic_{3})A|A|^{2}.$

Método FTCS

Para estudar o comportamento das soluções foi utilizados o método FTCS(Foward-Time Central-Space) explícito que consiste em discretizar o domínio temporal e o espacial da equação, resolvemos as derivadas espaciais por uma aproximação dos pontos vizinhos ao ponto que queremos encontrar, enquanto atualizamos a parte temporal, também por uma aproximação como na parte espacial, porém fazemos por diferenciação entre a taxa de variação (solução futura) e a solução atual. A partir da CGLE em duas dimensões: ${\frac {\partial A}{\partial t}}=\alpha ({\frac {\partial ^{2}A}{\partial x^{2}}}+{\frac {\partial ^{2}A}{\partial x^{2}}})+A-\beta A|A|^{2}.$

para

$\alpha =(1+ic_{1});\beta =(1-ic_{3})$

Aplicamos o método da seguinte maneira: ${\frac {A(x,y,t+\Delta t)-A(x,y,t)}{\Delta t}}=\alpha ({\frac {A(x+\Delta x,y,t)-2*A(x,y,t)+A(x-\Delta x,y,t)}{\Delta x^{2}}}+{\frac {A(x,y+\Delta y,t)-2*A(x,y,t)+A(x,y-\Delta y,t)}{\Delta y^{2}}})+A(x,y,t)-\beta A(x,y,t)|A(x,y,t)|^{2}.$

${\frac {A_{i,j}^{N+1}-A_{i,j}^{N}}{\Delta t}}=\alpha ({\frac {A_{i+1,j}^{N}-2*A_{i,j}^{N}+A_{i-1,j}^{N}}{\Delta x^{2}}}+{\frac {A_{i,j+1}^{N}-2*A_{i,j}^{N}+A_{i,j-1}^{N}}{\Delta y^{2}}})+A_{i,j}^{N}-\beta A_{i,j}^{N}|A_{i,j}^{N}|^{2}.$

Agora reorganizando a equação para deixar o tempo futuro na esquerda e o tempo atual na direita e considerando que os passos na direção x tem o mesmo tamanho do que os na direção y ($\Delta y=\Delta x$), chegamos em : $A_{i,j}^{N+1}=A_{i,j}(1+\Delta t(1-\beta |A_{i,j}|^{2}))+{\frac {\Delta t\alpha }{\Delta x^{2}}}(A_{i+1,j}+A_{i-1,j}+A_{i,j+1}+A_{i,j-1}-4*A_{i,j})$

Figura 2 - Condições de contorno periódicas em duas dimensões.

Para as condições de contorno foram utilizados condições periódicas tal que na região de x usamos que quando

i=L+1 estaremos em i=1.

e para y, da mesma forma,

j=L+1 temos que j=1.

A figura 2 é a representação gráfica dessas condições.

Soluções

Figura 3 - Diagrama de fase para soluções da CGLE [3].

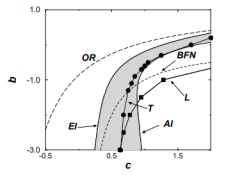
A partir da variação dos parâmetros c1 e c3 temos regiões que implicam em diferentes soluções para a CGLE, nossa ideia central foi começar com condição inicial de onda plana, que em teoria tende a se manter como onda plana, e perturbar essa solução, dependendo da região em que estamos no diagrama de fase a perturbação nos levara para diferentes tipos de solução sendo as principais:

• Soluções de onda plana estável
• Soluções de onda plana instável

que são delimitadas pela condição de Benjamin-Feir-Newell, que descreve a linha BFN no diagrama de fase, a condição para instabilidade é descrita por $1-c1c3<0$, ou seja, acima da linha temos soluções estáveis e abaixo soluções instáveis. Outras soluções que podem ser encontradas são soluções de turbulência, para fase e para a amplitude,

condição tipos de espirais -(c3 + c1)/(1 -c1*c3) = 0.845 Linha OR, interação entre espirais.

esquerda de T dinâmico turbulento, direita "congelado".

L limite da turbulência de fase

Eckhaus-stability boundary EI

boundary of absolute stability AI

Figura 4 -.

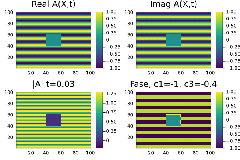
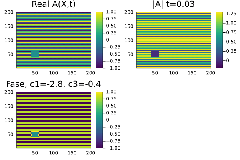
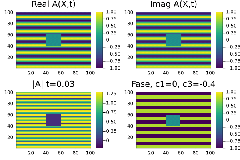
Quando definimos as condições iniciais de onda plana como um seno e um termo perturbando as ocilações em x=[40,60] y=[40,60], com b=-1, c=-0.4 do diagrama de fase em (figura3) o sistema apresenta simetria entre as espirais nos graficos real A() e imag A() também percebemos a presença de defeitos no modulo de A (figura 4). Esses defeitos nao se anularão

Figura 5 - .

Figura 6 - .

Referências

[1] García-Morales, V., & Krischer, K. (2012). The complex Ginzburg–Landau equation: an introduction. Contemporary Physics, 53(2), 79–95. https://doi.org/10.1080/00107514.2011.642554

[2] H. Riecke, (2021). Methods of Nonlinear Analysis

[3] Igor S. Aranson, Lorenz Kramer, (2001). The World of the Complex Ginzburg-Landau Equation

[4] Cross, M., & Greenside, H. (2009). Pattern Formation and Dynamics in Nonequilibrium Systems. Cambridge University Press.

[5] Hugues Chaté, Paul Manneville (1996). Phase diagram of the two-dimensional complex Ginzburg-Landau equation. Physica A: Statistical Mechanics and its Applications