Equação de Ginzburg-Landau complexa

A equação de Ginzburg-Landau complexa (CGLE) surgiu inicialmente em 1969 como um modelo para o inicio de instabilidades em problemas de convecção de fluídos. A partir de então, ela se tornou uma das equações não lineares mais estudadas da física, descrevendo uma variedade enorme de fenômenos como:

• Ondas não lineares;
• Transições de fase de segunda ordem;
• Supercondutividade;
• Superfluidez;
• Condensado de Bose-Einstein.

A equação de Ginzburg-Landau complexa, quando escrita de modo a minimizar o número de constantes, é dada pela equação abaixo:

${\frac {\partial A}{\partial t}}=(1+ic_{1})\nabla ^{2}A+A-(1-ic_{3})A|A|^{2}.$

É possível deduzir a CGLE a partir do oscilador linear harmônico por meio de argumentos de simetria, encontrando a equação de Stuart-Landau, e, em seguida, considerando um sistema estendido no espaço.

Dedução

Espaço de fase do oscilador harmônico

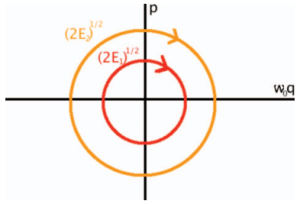
A energia de um oscilador harmônico é expressa pela equação abaixo, onde $E$ é a energia, $q$ e $p$ a coordenada e seu respectivo momento, $m$ é a massa e $\omega _{0}$ a frequência angular

$E={\frac {p^{2}}{2m}}+{\frac {1}{2}}m\omega _{0}^{2}q^{2}.$

Ao realizar as seguintes mudanças de variáveis, $q\rightarrow q/m^{1/2}$ e $p\rightarrow pm^{1/2}$, a equação da energia produz trajetórias circulares no espaço de fase de $\omega _{0}q$ e $p$

$E={\frac {p^{2}}{2}}+{\frac {1}{2}}\omega _{0}^{2}q^{2}.$

Essa é uma importante simetria do oscilador harmônico linear, resultando que a sua energia é proporcional ao quadrado da amplitude de oscilação, não dependendo da fase. Isso sugere uma motivação, qual é o menor termo não linear que pode ser adicionado de modo a preservar essa simetria. Para tanto, o estado do sistema será descrito em coordenadas polares, onde $R$ é a amplitude e $\phi$ a fase

${\dot {R}}=0,\quad {\dot {\phi }}=\omega _{0}.$

Define-se, então, a variável complexa $A=Re^{i\phi }$, portanto a equação acima pode ser reescrita como

${\dot {A}}=i\omega _{0}A.$

Ao realizar a transformação de variável $A\rightarrow Ae^{i\chi }$, com $\chi \in \mathbb {R}$, a equação acima permanece inalterada. Ou seja, a equação é invariante a rotações. Então, busca-se uma função não linear $f(A,A^{*})$ tal que

${\dot {A}}=i\omega _{0}A+f(A,A^{*})$

também seja invariante a rotações.

Então, perante às transformações $A\rightarrow Ae^{i\chi }$ e $A^{*}\rightarrow A^{*}e^{-i\chi }$, a função $f(A,A^{*})$ deve satisfazer

$f(Ae^{i\chi },A^{*}e^{-i\chi })=f(A,A^{*})e^{i\chi },$

para que seja possível fatorar o termo responsável pela rotação e obter novamente a equação original.

Considerando pequenas oscilações, é possível expandir $f(A,A^{*})$ em potências de $A$ e $A^{*}$ até a menor ordem possível que satisfaça a condição e que introduza uma não linearidade à equação. Com isso, obtém-se

$f(A,A^{*})=\alpha _{1}A+\alpha _{2}|A|^{2}A,\quad \alpha _{1}=\alpha _{1r}+i\alpha _{1i},\quad \alpha _{2}=\alpha _{2r}+i\alpha _{2i}$

Utilizando o resultado encontrado e expressando em coordenadas polares por meio de $A=Re^{i\phi }$

${\dot {R}}=\alpha _{1r}R+\alpha _{2r}R^{3},\quad {\dot {\phi }}=\omega _{0}+\alpha _{1i}+\alpha _{2i}R^{2}.$

Em seguida, muda-se para o referencial que gira com a mesma frequência do oscilador harmônico por meio da definição de $\phi =\varphi +\omega _{0}t$. As novas equações obtidas são

${\dot {R}}=\alpha _{1r}R+\alpha _{2r}R^{3},\quad {\dot {\varphi }}=\alpha _{1i}+\alpha _{2i}R^{2}.$

Para encontrar a amplitude estacionária, pode-se tomar ${\dot {R}}=0$ na equação, o que resulta na solução trivial $R^{(est)}=0$ e $R^{(est)}={\sqrt {-\alpha _{1r}/\alpha _{2r}}}$

Método FTCS

Para estudar o comportamento das soluções foi utilizados o método FTCS(Foward-Time Central-Space) que consiste em discretizar a solução temporal e a solução espacial da equação, resolvemos as derivadas espaciais por uma aproximação dos pontos vizinhos ao ponto que queremos encontrar, enquanto atualizamos a parte temporal, também por uma aproximação como na parte espacial porém fazemos por uma diferenciação entre a taxa de variação (solução futura) e a solução atual. A partir da CGLE em duas dimensões: ${\frac {\partial A}{\partial t}}=\alpha ({\frac {\partial ^{2}A}{\partial x^{2}}}+{\frac {\partial ^{2}A}{\partial x^{2}}})+A-\beta A|A|^{2}.$

para

$\alpha =(1+ic_{1});\beta =(1-ic_{1})$

Aplicamos o método da seguinte maneira: ${\frac {A(x,y,t+\Delta t)-A(x,y,t)}{\Delta t}}=\alpha ({\frac {A(x+\Delta x,y,t)-2*A(x,y,t)+A(x-\Delta x,y,t)}{\Delta x^{2}}}+{\frac {A(x,y+\Delta y,t)-2*A(x,y,t)+A(x,y-\Delta y,t)}{\Delta y^{2}}})+A(x,y,t)-\beta A(x,y,t)|A(x,y,t)|^{2}.$

${\frac {A_{i,j}^{N+1}-A_{i,j}^{N}}{\Delta t}}=\alpha ({\frac {A_{i+1,j}^{N}-2*A_{i,j}^{N}+A_{i-1,j}^{N}}{\Delta x^{2}}}+{\frac {A_{i,j+1}^{N}-2*A_{i,j}^{N}+A_{i,j-1}^{N}}{\Delta y^{2}}})+A_{i,j}^{N}-\beta A_{i,j}^{N}|A_{i,j}^{N}|^{2}.$

Agora reorganizando a equação para deixar o tempo futuro na esquerda e o tempo atual na direita e considerando que os passos na direção x tem o mesmo tamanho do que os na direção y ($\Delta y=\Delta x$), chegamos em : $A_{i,j}^{N+1}=A_{i,j}(1+\Delta t(1-\beta |A_{i,j}|^{2}))+{\frac {\Delta t\alpha }{\Delta x^{2}}}(A_{i+1,j}+A_{i-1,j}+A_{i,j+1}+A_{i,j-1}-4*A_{i,j})$