Corda Vibrante: mudanças entre as edições
(análise espectral: bases enumeráveis) |
(simulação de uma corda de violão) |
||
| Linha 16: | Linha 16: | ||
</center> | </center> | ||
E podemos extrair suas coordenadas (<math>a(\omega)</math> e <math>b(\omega)</math>), fazendo o produto escalar com os elementos da base | E podemos extrair suas coordenadas (também chamadas de transformada de fourier do sinal) (<math>a(\omega)</math> e <math>b(\omega)</math>), fazendo o produto escalar com os elementos da base | ||
<center> | <center> | ||
| Linha 40: | Linha 40: | ||
</center> | </center> | ||
É impossível falar sobre bases enumeráveis de um sub-espaço de <math> \mathbb{R}^{\mathbb{R}} </math> sem representar esse canhão matemático com uma animação. Abaixo segue uma | É impossível falar sobre bases enumeráveis de um sub-espaço de <math> \mathbb{R}^{\mathbb{R}} </math> sem representar esse canhão matemático com uma animação. Abaixo segue uma visualização que calcula as primeiras <math>N</math> coordenadas (<math>a_0,\dots,a_N</math> e <math>b_1,\dots,b_N</math>) de um sinal qualquer e sobrepõem a série obtida incrementando <math>N</math> até as duas curvas serem indistinguíveis a olho nu. | ||
Agora, considerando uma corda vibrante, o | <center> | ||
[[Arquivo:Serie_fourier_ana_julia.gif|frame|center|Animação de uma série de fourier. É interessante notar que a série converge muito bem com apenas uma dúzia de frequências.]] | |||
</center> | |||
=== Potência espectral === | |||
Agora, considerando uma corda vibrante, adiante vamos ver que o sinal sonoro provém da vibração de um ponto específico da mesma, digamos em <math>x=x_o</math>, então a função que representa esse sinal é <math>y(x_o, t)</math>. Como estamos interessados nas frequências que compõem o sinal, será calculado a transformada de fourier de <math>y(x_o, t)</math> e vamos definir que a potência da frequência <math>f = \omega/(2\pi)</math> é <math>a_\omega^2 + b_\omega^2</math>. A potência em função da frequência é o resultado da análise espectral. | |||
== Simulando uma corda de violão == | |||
Uma corda de violão geralmente é excitada por uma pancada dada por uma palheta ou pelo próprio dedo/unha do violonista. Essa pancada define uma condição inicial para a equação de onda. Uma suposição razoável da condição gerada é a seguinte | |||
<math> | |||
\begin{aligned} | |||
y(x, t=0) &= \begin{cases} | |||
\frac{h}{x_0}x &, ~ 0 \leq x \leq x_0\\ | |||
\frac{h}{L-x_0}(-x + L) &, ~ x_0 \leq x \leq L\\ | |||
\end{cases} \\ | |||
\frac{\partial}{\partial t} y(x, t=0) &= 0 | |||
\end{aligned} | |||
</math> | |||
supondo que a corda possui comprimento <math>L</math> e a pancado ocorreu em <math>x_o</math>, causando uma deslocamento máximo <math>h</math>. A imagem a seguir ilustra o estado da corda logo após a excitação | |||
<center> | |||
[[Arquivo:Init_cond_ana_julia.png|thumb|upright=2|center|Condição inicial de uma corda de violão.]] | |||
</center> | |||
Dado essa condição inicial, podemos evoluir temporalmente o estado da corda utilizando a equação da onda, mantendo as bordas fixas (<math>y(x=0, t) = y(x=L, t) = 0</math>), mas como extrair som dessa simulação? Para responder essa pergunta precisamos saber como um violão gera som. Ao contrário do que inicialmente pareça, as ondas sonoras não são diretamente geradas pela vibração das cordas, mas sim da caixa do violão, que está diretamente conectada com as cordas em uma peça chamada ponte. A vibração das cordas gera uma força dependente do tempo que atua na caixa através da ponte, assim vibrando a caixa e gerando o som que escutamos. Portanto, para gerar som de forma realista, precisaríamos fisicamente simular a caixa, levando em consideração a sua geometria e as propriedades física do seu material, e então determinar as ondas de pressão que seriam geradas por essa vibração, o que está fora do escopo do presente trabalho. Felizmente, as seguintes simplificações vão nos permitir calcular as ondas de pressão: | |||
* A força que a ponte exerce na caixa é aproximadamente proporcional a sua velocidade (Dinâmica aristotélica). | |||
* A onda de pressão produzida pela caixa é aproximadamente proporcional a sua velocidade. | |||
A força que a ponte exercer na caixa (<math>F(t)</math>) é a força que a corda exerce na ponte (pois a ponte está firmemente conectada na caixa), e essa força é proporcional a inclinação da corda, ou seja | |||
<center> | |||
<math> | |||
F(t) = T \frac{\partial}{\partial x}y(x=0, t) \approx T\frac{y(\Delta x, t) - \overbrace{y(0, t)}^{0}}{\Delta x} = \frac{T}{\Delta x} y(\Delta x, t) | |||
</math> | |||
</center> | |||
em que <math>T</math> é a tensão na corda. Portando, o sinal da onda de pressão pode ser aproximado como o deslocamento de um ponto da corda próximo a ponte. Para gerar som com esse sinal, o tipo de arquivo [https://en.wikipedia.org/wiki/WAV#:~:text=Waveform%20Audio%20File%20Format%20(WAVE,1991%20by%20IBM%20and%20Microsoft. WAV]] é utilizado, pois o seu dado de entrada pode ser justante o sinal da onda de pressão. | |||
Agora tudo está pronto para fazermos uma simulação, vamos tentar reproduzir a nota lá (<math>f = 440</math> Hz). Primeiro precisamos descobrir qual deve ser a velocidade de propagação das ondas (<math>c</math>) para gerar a nota em questão. Resolvendo a equação da onda ideal, obtemos que as possíveis frequência que existem na solução são <math>f_n = \frac{nc}{2L} </math>, então não é possível fazer a corda vibrar apenas com uma frequência, mas quando músicos se referem a uma nota, eles realmente estão se referindo a <math>f_1</math>, a primeira frequência que compõem o sinal, então | |||
<center> | |||
<math> f_1 = \frac{c}{2L} = 440~Hz \Rightarrow c = L \cdot 880 Hz</math> | |||
</center> | |||
Assumindo <math>L=1~m</math>, temos que <math>c = 880~m/s</math>. Resolvendo a equação da onda realista pela método FTCS com os seguinte parâmetros | |||
{| class="wikitable" | |||
|+ Parâmetros da condição inicial | |||
|- | |||
! Parâmetros !! Valor | |||
|- | |||
| x_o || <math>0,5 L</math> | |||
|- | |||
| h || 1 cm | |||
|} | |||
{| class="wikitable" | |||
|+ Parâmetros da integração | |||
|- | |||
! Parâmetros !! Valor | |||
|- | |||
| k || 1/4 | |||
|- | |||
| c || 880 m/s | |||
|- | |||
| <math>\Delta x</math> || 0.01 m | |||
|- | |||
| L || 1 m | |||
|- | |||
| b || 5 1/s | |||
|- | |||
| <math>\epsilon</math> || <math>10^{-9}</math> | |||
|} | |||
obtemos o seguinte resultado | |||
[[Arquivo:Corda_vibrando_ana_julia.gif|frame|center|Solução da equação de onda ideal e realista.]] | |||
Na animação acima, por questão de comparação, também foi coloca a solução de uma simulação com os mesmos parâmetros, apenas com a modificação <math>b=\epsilon=0</math>, que seria o caso ideal (sem amortecimento e rigidez). | |||
Realizando a análise espectral do deslocamento de um ponto próximo de <math>x=0</math>, obtemos o seguinte gráfico | |||
<center> | |||
[[Arquivo:La_power_ana_julia.png |thumb|upright=2|center|Espectro do deslocamento de um ponto próximo de <math>x=0</math>]] | |||
</center> | |||
As linhas verticais pretas e tracejadas representam as possíveis frequências da solução do caso ideal, ou seja, a primeira linha está em <math>f = 440 Hz </math> como era de se esperar, mas é notável que a segunda e quarta linhas possuem uma potência praticamente nula, isso ocorre porque a excitação inicial foi exatamente no meio, e as frequência correspondentes a essas linhas provém de ondas estacionário que possum um nodo em <math>x=L/2</math>, logo elas não foram excitadas pela condição inicial. Mudando o ponto de excitação inicial, podemos ver essas frequências aparecendo, rodando a simulação novamente, mas com <math>x_o = 0.2L</math>, obtemos o seguinte espectro | |||
<center> | |||
[[Arquivo:La_power_bridge_ana_julia.png |thumb|upright=2|center|Espectro do deslocamento de um ponto próximo de <math>x=0</math>]] | |||
</center> | |||
Por fim, conforme descrito anteriormente, podemos gerar som com as dados da simulação, mas infelizmente essa wiki não nos permite upar arquivos de áudio. No entanto, áudio das duas simulações discutidas podem ser encontrados no repositório do projeto [https://github.com/marcos1561/ana-julia ana-julia] dentro da pasta "sound". | |||
== Notas == | == Notas == | ||
Edição das 17h33min de 20 de abril de 2024
A equação da onda
Método FTCS
Sobre estabilidade
Análise espectral
Uma possível forma para quantitativamente analisar o som gerado por uma corda vibrante é estudar as frequências que compõem o seu movimento, técnica essa chamada de análise espectral. Antes de prosseguirmos vamos recapitular alguns resultados da álgebra linear
Supremacia da álgebra linear
O seguinte conjunto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^{\mathbb{R}} = \{ f~|~f: \mathbb{R} \to \mathbb{R} \} } é o espaço de funções reais de uma variável. Esse conjunto é um espaço vetorial, logo podemos utilizar toda a artilharia da álgebra linear, em especial, estamos interessados no sub-espaço gerado pela base Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B = \{sen(\omega t) / \sqrt{\pi}, cos(\omega t) / \sqrt{\pi} \}_{\omega \in \mathbb{R^+}} } [1], pois elementos de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle B } , interpretados como sinais sonoros, representam um frequência pura de valor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f=\omega/(2\pi)} . Dessa forma, um sinal arbitrário Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s(t)} pode ser escrito em termos das frequências puras que o formam
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s(t) = \frac{1}{\sqrt{\pi}}\int_{0}^{\infty}[a(\omega)cos(\omega t) + b(\omega)sen(\omega t]d\omega }
E podemos extrair suas coordenadas (também chamadas de transformada de fourier do sinal) (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a(\omega)} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle b(\omega)} ), fazendo o produto escalar com os elementos da base
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{aligned} a(\omega) &= \int_{-\infty}^{\infty}s(t)\frac{1}{\sqrt{\pi}}cos(\omega t)dt \\ b(\omega) &= \int_{-\infty}^{\infty}s(t)\frac{1}{\sqrt{\pi}}sen(\omega t)dt \end{aligned} }
Se o domínio de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s(t)} é limitado, digamos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t \in [0, T]} , então uma base infinita com cardinalidade enumerável (em contraste com a base anterior, que possui cardinalidade não enumerável) é suficiente para representar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s(t)} , uma possível base ortonormal é a seguinte: Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigg\{ \sqrt{\frac{1}{T}}, \sqrt{\frac{2}{T}}sen(\omega_n t), \sqrt{\frac{2}{T}}cos(\omega_n t) \bigg\}_{n \in \mathbb{N^*}}} , em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_n = \frac{n\pi}{T} } . Dessa forma, a representação e coordenadas de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s(t)} ficam
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{aligned} s(t) &= a_0\sqrt{\frac{1}{T}} + \sqrt{\frac{2}{T}}\sum_{n=1}^{\infty}\bigg[a_n cos(\omega_n t) + b_n sen(\omega_n) \bigg] \\ a_0 &= \int_0^T s(t) \sqrt{\frac{1}{T}}dt \\ a_n &= \int_0^T s(t) \sqrt{\frac{2}{T}}cos(\omega_n t)dt \\ b_n &= \int_0^T s(t) \sqrt{\frac{2}{T}}sen(\omega_n t)dt \\ \end{aligned} }
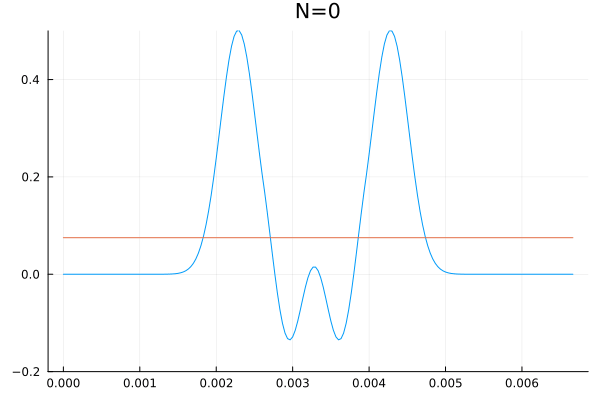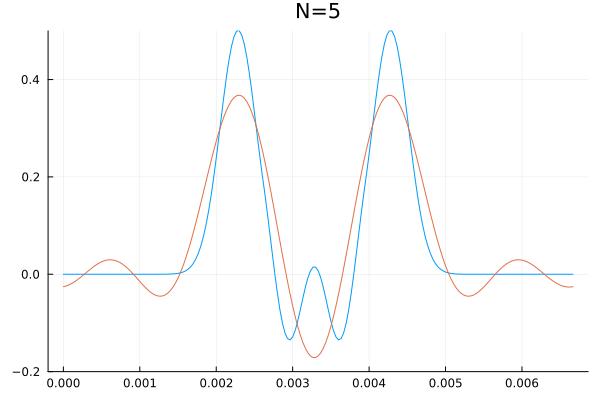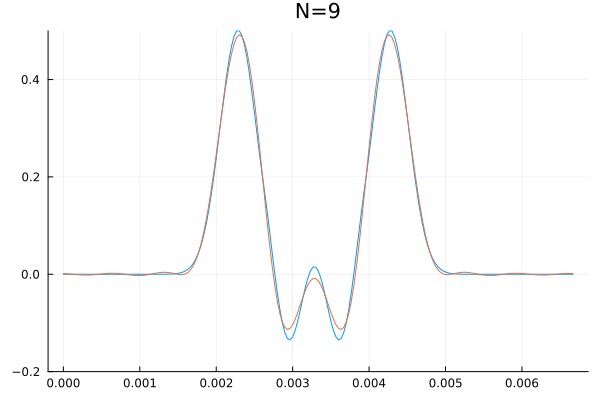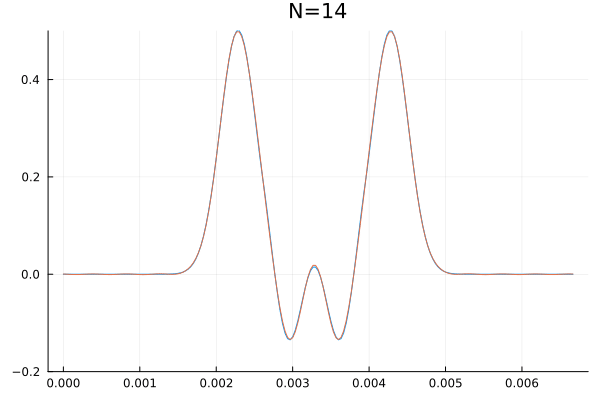
É impossível falar sobre bases enumeráveis de um sub-espaço de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^{\mathbb{R}} } sem representar esse canhão matemático com uma animação. Abaixo segue uma visualização que calcula as primeiras Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} coordenadas (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_0,\dots,a_N} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_1,\dots,b_N} ) de um sinal qualquer e sobrepõem a série obtida incrementando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} até as duas curvas serem indistinguíveis a olho nu.
Potência espectral
Agora, considerando uma corda vibrante, adiante vamos ver que o sinal sonoro provém da vibração de um ponto específico da mesma, digamos em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=x_o} , então a função que representa esse sinal é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y(x_o, t)} . Como estamos interessados nas frequências que compõem o sinal, será calculado a transformada de fourier de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y(x_o, t)} e vamos definir que a potência da frequência Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = \omega/(2\pi)} é Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_\omega^2 + b_\omega^2} . A potência em função da frequência é o resultado da análise espectral.
Simulando uma corda de violão
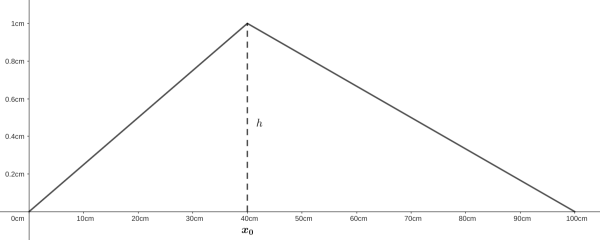
Uma corda de violão geralmente é excitada por uma pancada dada por uma palheta ou pelo próprio dedo/unha do violonista. Essa pancada define uma condição inicial para a equação de onda. Uma suposição razoável da condição gerada é a seguinte
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{aligned} y(x, t=0) &= \begin{cases} \frac{h}{x_0}x &, ~ 0 \leq x \leq x_0\\ \frac{h}{L-x_0}(-x + L) &, ~ x_0 \leq x \leq L\\ \end{cases} \\ \frac{\partial}{\partial t} y(x, t=0) &= 0 \end{aligned} }
supondo que a corda possui comprimento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} e a pancado ocorreu em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_o} , causando uma deslocamento máximo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} . A imagem a seguir ilustra o estado da corda logo após a excitação
Dado essa condição inicial, podemos evoluir temporalmente o estado da corda utilizando a equação da onda, mantendo as bordas fixas (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y(x=0, t) = y(x=L, t) = 0} ), mas como extrair som dessa simulação? Para responder essa pergunta precisamos saber como um violão gera som. Ao contrário do que inicialmente pareça, as ondas sonoras não são diretamente geradas pela vibração das cordas, mas sim da caixa do violão, que está diretamente conectada com as cordas em uma peça chamada ponte. A vibração das cordas gera uma força dependente do tempo que atua na caixa através da ponte, assim vibrando a caixa e gerando o som que escutamos. Portanto, para gerar som de forma realista, precisaríamos fisicamente simular a caixa, levando em consideração a sua geometria e as propriedades física do seu material, e então determinar as ondas de pressão que seriam geradas por essa vibração, o que está fora do escopo do presente trabalho. Felizmente, as seguintes simplificações vão nos permitir calcular as ondas de pressão:
- A força que a ponte exerce na caixa é aproximadamente proporcional a sua velocidade (Dinâmica aristotélica).
- A onda de pressão produzida pela caixa é aproximadamente proporcional a sua velocidade.
A força que a ponte exercer na caixa (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(t)} ) é a força que a corda exerce na ponte (pois a ponte está firmemente conectada na caixa), e essa força é proporcional a inclinação da corda, ou seja
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(t) = T \frac{\partial}{\partial x}y(x=0, t) \approx T\frac{y(\Delta x, t) - \overbrace{y(0, t)}^{0}}{\Delta x} = \frac{T}{\Delta x} y(\Delta x, t) }
em que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} é a tensão na corda. Portando, o sinal da onda de pressão pode ser aproximado como o deslocamento de um ponto da corda próximo a ponte. Para gerar som com esse sinal, o tipo de arquivo WAV] é utilizado, pois o seu dado de entrada pode ser justante o sinal da onda de pressão.
Agora tudo está pronto para fazermos uma simulação, vamos tentar reproduzir a nota lá (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = 440} Hz). Primeiro precisamos descobrir qual deve ser a velocidade de propagação das ondas (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} ) para gerar a nota em questão. Resolvendo a equação da onda ideal, obtemos que as possíveis frequência que existem na solução são Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_n = \frac{nc}{2L} } , então não é possível fazer a corda vibrar apenas com uma frequência, mas quando músicos se referem a uma nota, eles realmente estão se referindo a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_1} , a primeira frequência que compõem o sinal, então
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_1 = \frac{c}{2L} = 440~Hz \Rightarrow c = L \cdot 880 Hz}
Assumindo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L=1~m} , temos que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle c = 880~m/s} . Resolvendo a equação da onda realista pela método FTCS com os seguinte parâmetros
| Parâmetros | Valor |
|---|---|
| x_o | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0,5 L} |
| h | 1 cm |
| Parâmetros | Valor |
|---|---|
| k | 1/4 |
| c | 880 m/s |
| Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x} | 0.01 m |
| L | 1 m |
| b | 5 1/s |
| Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-9}} |
obtemos o seguinte resultado
Na animação acima, por questão de comparação, também foi coloca a solução de uma simulação com os mesmos parâmetros, apenas com a modificação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle b=\epsilon=0} , que seria o caso ideal (sem amortecimento e rigidez).
Realizando a análise espectral do deslocamento de um ponto próximo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0} , obtemos o seguinte gráfico
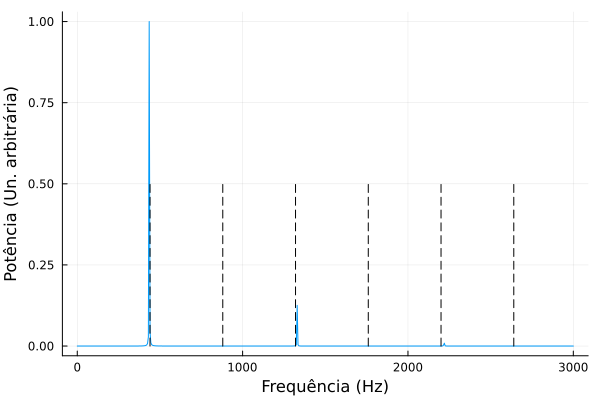
As linhas verticais pretas e tracejadas representam as possíveis frequências da solução do caso ideal, ou seja, a primeira linha está em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = 440 Hz } como era de se esperar, mas é notável que a segunda e quarta linhas possuem uma potência praticamente nula, isso ocorre porque a excitação inicial foi exatamente no meio, e as frequência correspondentes a essas linhas provém de ondas estacionário que possum um nodo em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=L/2} , logo elas não foram excitadas pela condição inicial. Mudando o ponto de excitação inicial, podemos ver essas frequências aparecendo, rodando a simulação novamente, mas com , obtemos o seguinte espectro
Por fim, conforme descrito anteriormente, podemos gerar som com as dados da simulação, mas infelizmente essa wiki não nos permite upar arquivos de áudio. No entanto, áudio das duas simulações discutidas podem ser encontrados no repositório do projeto ana-julia dentro da pasta "sound".
Notas
- ↑ A constante está presente por questão de normalização. Esse caso pode parecer um pouco estranho, dado que não é possível normalizar os cossenos e senos, pois sua integral em todo a reta não é definida, mas o que se deseja é a seguinte propriedade que é safisfeita quando