Equação de Kuramoto–Sivashinsky

André Becho Guimarães

Este trabalho tem como objetivo estudar o comportamento das soluções para a equação de Kuramoto-Sivashinsky de contorno periódico, para isso são utilizados dois métodos: diferenças finitas e fast fourier transform. Os resultados obtidos são apresentados e discussões são feitas sob à luz da teoria de caos.

Equação

A equação de Kuramoto-Sivashinsky (KS) foi inicialmente proposta por Yoshiki Kuramoto e Gregory Sivashinsky para a modelagem das instabilidades da frente de uma chama laminar.

$u_{t}+u_{xx}+u_{xxxx}+{\frac {1}{2}}u_{x}^{2}=0$

No entanto, a forma diferencial $v=u_{x}$ da equação foi descoberta independentemente na área de dinâmica de fluidos, onde ficou mais conhecida para a modelagem de filmes finos.

$v_{t}+v_{xx}+v_{xxxx}+vv_{x}=0$

A equação apresenta comportamentos caóticos ao ser estudada em geometrias anelares, ou seja, condições de contorno periódicas; por isso esse será o caso estudado aqui.

Métodos de Solução

Diferenças Finitas (FTCS)

O método mais simples foi aplicado a fim de entender o comportamento da equação. Tentativas de linearização resultaram em uma equação de comportamento muito distinto do descrito na literatura; e portanto, não é de nosso interesse estudá-la. É importante relembrar que a aplicação do método FTCS não é recomendado no caso de não linearidades pois o método tem baixa precisão e pode acumular erros.

Como esperado, a solução numérica teve sua estabilidade atrelada à suas condições iniciais; ou seja, a solução é instável (exceto em casos bem específicos, onde ela se comporta de forma análoga à equação da difusão).

Solução FTCS de condição inicial $\sin {\left({\frac {\pi }{20}}x\right)}^{2}$

Solução FTCS de condição inicial $\sin {\left({\frac {\pi }{10}}x\right)}^{2}$

Método Espectral (FFT)

Utilizando o método fft em conjunto com as propriedades da transformada de fourier, pode-se resolver a EDP utilizando a forma de derivada espectral. Esse método possui alta precisão e é capaz de incorporar o comportamento ondulatório de soluções, algo característico da equação de Kuramoto-Sivashinsky.

A derivada espectral é caracterizada pela transformada de fourier de uma derivada, o que facilita a resolução de equações diferenciais parciais:

${\mathcal {F}}(v_{x})=ik{\mathcal {F}}(v)\longrightarrow v_{x}={\mathcal {F^{-1}}}\left(ik{\mathcal {F}}(v)\right)$.

Essa propriedade permite que a resolução da parte espacial da equação de Kuramoto-Sivashinsky diferencial seja dada por

$v_{t}={\mathcal {F^{-1}}}(k^{2}{\hat {v}})-{\mathcal {F^{-1}}}(k^{4}{\hat {v}})-{\frac {v{\mathcal {F^{-1}}}(ik{\hat {v}})}{2}}$,

onde ${\hat {v}}\equiv {\mathcal {F}}(v)$. A parte temporal também pode ser resolvida da mesma forma, mas o método de Runge-Kutta (RK45) foi aplicado em seu lugar por sua maior simplicidade e velocidade de processamento.

Resultados e Discussões

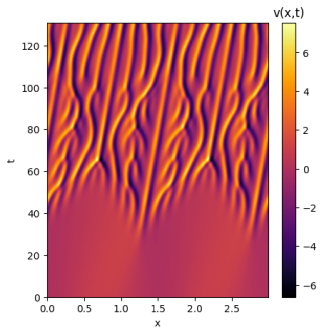
Através do método espectral foi possível estudar o comportamento da Equação de Kuramoto-Sivashinsky em sua forma diferencial. Para uma melhor interpretação das soluções, os dados são dispostos em dois modelos de gráfico: um gif em que a passagem de tempo é representada pela mudança de frames, e um gráfico com escala de cores; onde os eixos representam o tempo e o espaço.

Solução espectral de condição inicial $\sin {\left({\frac {2\pi }{3}}x\right)}^{2}$

Mapa temporal de condição inicial $\sin {\left({\frac {2\pi }{3}}x\right)}^{2}$

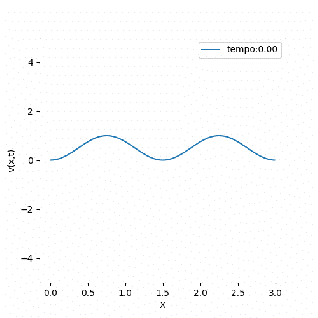
Ao partir de uma condição inicial senoidal, a equação se mantém estável por longos períodos de tempo, o que atrasa a chegada de seu comportamento mais característico: a formação de faixas. Esse comportamento é mais perceptível ao se analisar o mapa temporal da solução, deixando clara a tendência da equação de concentrar mínimos e máximos próximos, gerando picos e vales que se relacionam de forma complexa. No entanto, é fácil perceber que o comportamento simulado não é caótico e sim quase periódico. Isso está atrelado a um fator muito importante para o estudo da equação, o tamanho da periodicidade simulada, ou seja, seu domínio (L).

Caos gerado pelo Domínio (L)

É esperado que a solução para a equação dependa das condições iniciais escolhidas, mas uma relação entre a solução e o tamanho do domínio estudado é algo bem mais surpreendente. A equação KS apresenta esse comportamento inesperado e por isso é objeto de estudo até mesmo em teorias de caos. Sua forma simples apresenta três elementos importantes:

Um termo crescente, com funcionamento inverso à equação do calor:

$-v_{xx}$;

um termo dissipador, responsável pelo amortecimento de picos e vales estreitos:

$-v_{xxxx}$;

e um termo não linear, provavelmente responsável pelo comportamento ondulatório da equação, transferindo energia entre os estados crescentes e amortecidos:

$-vv_{x}$.

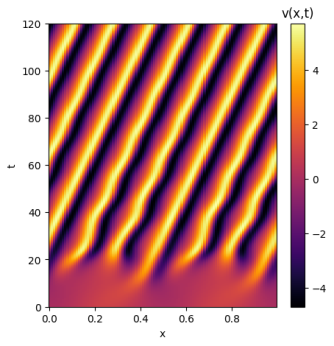
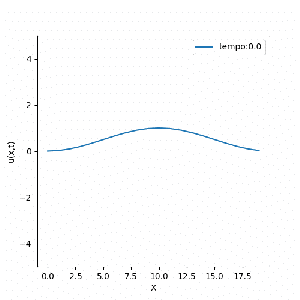
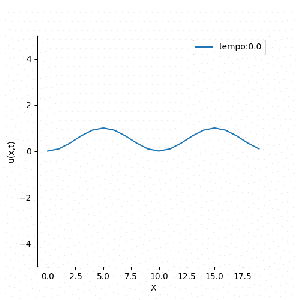
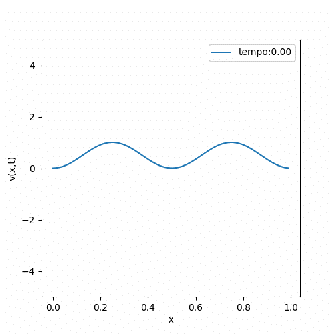
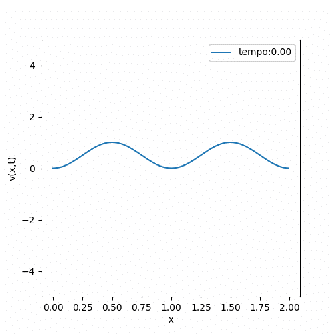
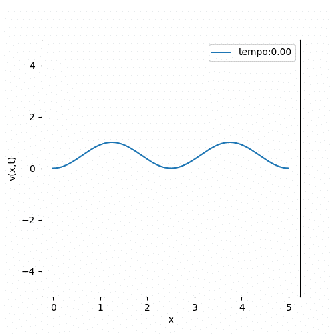
A soma desses comportamentos faz com que em domínios periódicos pequenos, a equação consiga se manter estável, atingindo resultados constantes ou ondas planas. Isso pode ser identificado nas soluções abaixo, que apesar de possuírem a mesma condição inicial ( $\sin {\left({\frac {2\pi }{L}}x\right)}^{2}$ ), são mapeadas em domínios de tamanhos diferentes.

Solução espectral para $L=1$

Mapa temporal para $L=1$

Solução espectral para $L=2$

Mapa temporal para $L=2$

Solução espectral para $L=5$

Mapa temporal para $L=5$

É notável a diferença entre as soluções encontradas, mas alguns pontos merecem destaque. Primeiramente existe uma forte relação entre a mudança de fase da equação e seu domínio, ou seja, domínios pequenos são atraídos mais rapidamente para a solução final; enquanto domínios maiores tendem a se manter estáveis por mais tempo. Por outro lado, a solução final tem forma mais simples para domínios pequenos, enquanto domínios maiores tendem a apresentar padrões mais intrincados.

A fim de estudar o caos gerado pela equação, é necessário que pequenas variações (ruído) sejam inseridas. Para tanto, a condição inicial se manteve a mesma já estudada, mas somada à valores gerados aleatoriamente a partir do intervalo $[-0.01,0.01]$ para cada ponto do domínio.

Mapa temporal para $L=1$ sem ruído

Mapa temporal para $L=2$ sem ruído

Mapa temporal para $L=5$ sem ruído

Mapa temporal para $L=1$ com ruído

Mapa temporal para $L=2$ com ruído

Mapa temporal para $L=5$ com ruído

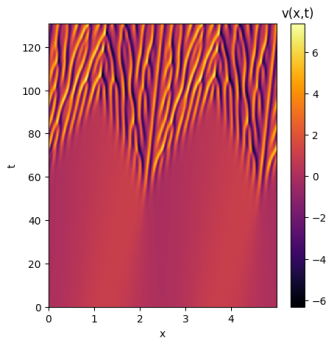
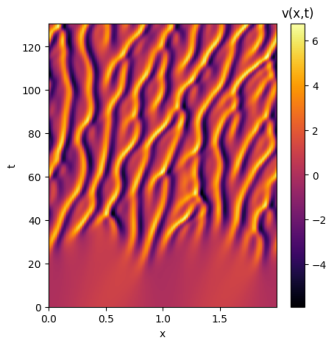
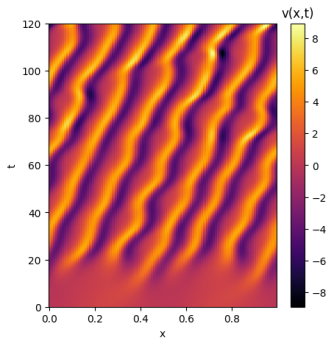
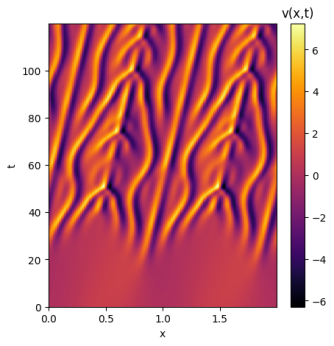
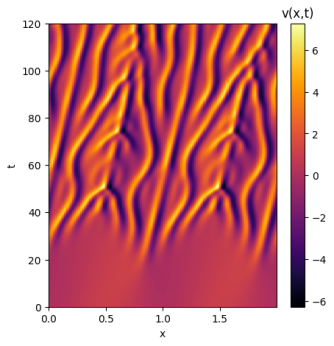
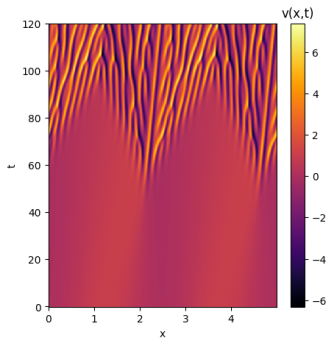
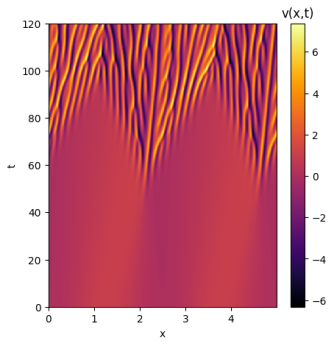
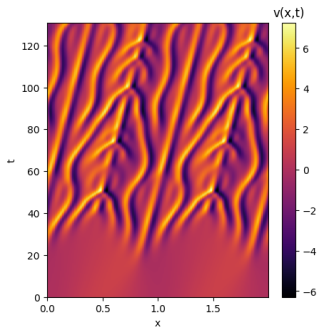
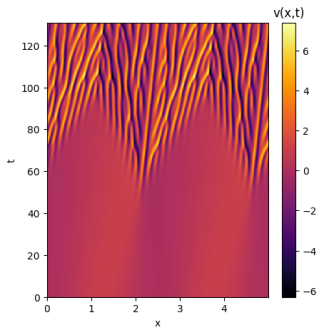
Ao analisar as soluções com ruído é possível perceber a sensibilidade de cada solução às condições iniciais. A solução de domínio $L=1$ se manteve quase inalterada, atingindo um resultado muito similar ao da solução original. Já o domínio $L=2$ apresentou uma sensibilidade muito maior às pequenas variações do ruído; inicialmente a solução aparenta seguir o mesmo caminho, mas aos poucos deformidades começam a surgir e a solução perde suas simetrias e periodicidades. Por fim, a solução de domínio $L=5$ teve seu comportamento quase completamente alterado; sua maior estabilidade deixa de estar presente e seus padrões não apresentam qualquer simetria.

Como é possível perceber, com o aumento de L as soluções para a equação de Kuramoto-Sivashinsky se tornam caóticas, apresentando padrões muito sensíveis às condições iniciais. Para entender melhor a sensibilidade de cada domínio, as soluções a seguir terão um único ponto de diferença entre si: seu ponto central será somado a valores levemente maiores até que seu comportamento geral seja alterado. Isso permitirá identificar os limites de atração para as soluções de cada domínio. Para fins de melhor comparação, a condição inicial já utilizada será repetida para todos os domínios: $\sin {\left({\frac {2\pi }{L}}x\right)}^{2}$.

Antes de analisar os resultados é importante destacar um ponto essencial da implementação do algoritmo: a discretização espacial é feita de forma a manter "dx" constante, independentemente do tamanho do domínio estudado. Ou seja, ao aumentar o tamanho do domínio, sua resolução permanece inalterada. Isso torna o algoritmo mais preciso, permitindo que domínios maiores mantenham a mesma precisão de domínios menores. Por outro lado, isso torna o processamento de domínios maiores lento e ineficaz, limitando o estudo a domínios de escala próxima a $L=10$.

Domínio L=1

Mapa temporal para $L=1$ com ruído pontual 0

Mapa temporal para $L=1$ com ruído pontual 0.405326

Para o domínio $L=1$ o comportamento da solução quase não é alterado pela alteração de um único ponto, é necessária uma alteração significativa para que o comportamento comece a se alterar. O ponto preciso de transição é infinitesimal e por isso não é possível definir um limite exato; mas para os testes feitos, é possível dizer com segurança que a transição entre as soluções ocorre para alterações de aproximadamente $\pm 0.405326$ em um único ponto. É fácil perceber mudanças gerais de comportamento que tornaram as faixas mais oscilantes e menos estáveis; além de um aumento da diferença entre mínimos e máximos.

Domínio L=2

Mapa temporal para $L=2$ com ruído pontual 0

Mapa temporal para $L=2$ com ruído pontual 0.00005

Para o domínio $L=2$ o comportamento da solução é bem sensível à alterações de um único ponto, é suficiente uma pequena alteração para que o comportamento comece a se alterar. O ponto preciso de transição é infinitesimal e por isso não é possível definir um limite exato; mas para os testes feitos, é possível dizer com segurança que a transição entre as soluções ocorre para alterações de aproximadamente $\pm 0.00005$ em um único ponto. É fácil perceber pequenas mudanças de comportamento na solução, principalmente a partir de $t=100$.

Domínio L=5

Mapa temporal para $L=5$ com ruído pontual 0

Mapa temporal para $L=5$ com ruído pontual 0.0000001

Para o domínio $L=5$ o comportamento da solução é extremamente sensível à alterações de um único ponto, é suficiente uma alteração quase infinitesimal para que o comportamento comece a se alterar. O ponto preciso de transição é infinitesimal e por isso não é possível definir um limite exato; mas para os testes feitos, é possível dizer com segurança que a transição entre as soluções ocorre para alterações de aproximadamente $\pm 0.0000001$ em um único ponto. As alterações geradas em um único ponto demoram a se espalhar em um domínio tão grande, mas já é possível notar uma quebra de simetria na parte central da solução, principalmente a partir de $t=100$.

Códigos em Python

Diferenças Finitas (FTCS)

#Importação de bibliotecas
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
import glob


#Parâmetros Gerais
h = 1
dt = 1/20
k = dt/h
beta = 0
m = 1

L = 20
t_max = 260
X = np.arange(L)
plot = 1


#Declaração das condições iniciais
F = np.zeros(L)
for i in range(L):
  F[i] = np.sin(2*np.pi*i/L)**2
G = F.copy()
t = 0

V = np.zeros((t_max,L))
T = np.arange(t,t_max) * k*h


#Atualização temporal
while t < t_max:
  V[t][0:] = F[0:]
  if t%10==0:
    fig = plt.figure(figsize=(5,5))
    plt.plot(X,F,label='tempo:{}'.format(t*k*h))
    plt.xlabel("X")
    plt.ylabel("u(x,t)")
    plt.legend()
    plt.ylim(-5,5)
    fig.savefig('./grafs/%c.PNG'% (plot))
    plt.close()
    plot+=1

  #Casos extremo esquerdo com contorno periódico
  G[0] = F[0] + k * F[0]**m * (F[L-1] - F[1]) + k*beta/h**2 * (F[L-3] - F[3] + 3 * (F[1] - F[L-1])) + k/h**3 * ((4-h**2) * (F[2] + F[L-2]) + F[0] * (2*h**2 - 6) - F[4] - F[L-4])
  G[1] = F[1] + k * F[1]**m * (F[0  ] - F[2]) + k*beta/h**2 * (F[L-2] - F[4] + 3 * (F[2] - F[0  ])) + k/h**3 * ((4-h**2) * (F[3] + F[L-1]) + F[1] * (2*h**2 - 6) - F[5] - F[L-3])
  G[2] = F[2] + k * F[2]**m * (F[1  ] - F[3]) + k*beta/h**2 * (F[L-1] - F[5] + 3 * (F[3] - F[1  ])) + k/h**3 * ((4-h**2) * (F[4] + F[0  ]) + F[2] * (2*h**2 - 6) - F[6] - F[L-2])
  G[3] = F[3] + k * F[3]**m * (F[2  ] - F[4]) + k*beta/h**2 * (F[0  ] - F[6] + 3 * (F[4] - F[2  ])) + k/h**3 * ((4-h**2) * (F[5] + F[1  ]) + F[3] * (2*h**2 - 6) - F[7] - F[L-1])

  #Casos gerais com contorno periódico
  G[4:L-4] = F[4:L-4] + k * F[4:L-4]**m * (F[3:L-5] - F[5:L-3]) + k*beta/h**2 * (F[1:L-7] - F[7:L-1] + 3 * (F[5:L-3] - F[3:L-5])) + k/h**3 * ((4-h**2) * (F[6:L-2] + F[2:L-6]) + F[4:L-4] * (2*h**2 - 6) - F[8:] - F[0:L-8])


  #Casos extremo direito com contorno periódico
  G[L-4] = F[L-4] + k * F[L-4]**m * (F[L-5] - F[L-3]) + k*beta/h**2 * (F[L-7] - F[L-1] + 3 * (F[L-3] - F[L-5])) + k/h**3 * ((4-h**2) * (F[L-2] + F[L-6]) + F[L-4] * (2*h**2 - 6) - F[0] - F[L-8])
  G[L-3] = F[L-3] + k * F[L-3]**m * (F[L-4] - F[L-2]) + k*beta/h**2 * (F[L-6] - F[0  ] + 3 * (F[L-2] - F[L-4])) + k/h**3 * ((4-h**2) * (F[L-1] + F[L-5]) + F[L-3] * (2*h**2 - 6) - F[1] - F[L-7])
  G[L-2] = F[L-2] + k * F[L-2]**m * (F[L-3] - F[L-1]) + k*beta/h**2 * (F[L-5] - F[1  ] + 3 * (F[L-1] - F[L-3])) + k/h**3 * ((4-h**2) * (F[0  ] + F[L-4]) + F[L-2] * (2*h**2 - 6) - F[2] - F[L-6])
  G[L-1] = F[L-1] + k * F[L-1]**m * (F[L-2] - F[0  ]) + k*beta/h**2 * (F[L-4] - F[2  ] + 3 * (F[0  ] - F[L-2])) + k/h**3 * ((4-h**2) * (F[1  ] + F[L-3]) + F[L-1] * (2*h**2 - 6) - F[3] - F[L-5])

  #Propagação para próxima iteração
  F = G.copy()
  t +=1


#Criação do GIF
frames = (Image.open(f) for f in sorted(glob.glob("./grafs/*.PNG")))
frame_one = next(frames)
frame_one.save("animado.gif", format="GIF", append_images=frames, save_all=True, duration=300, loop=0)

Método Espectral (FFT)

#Importação de bibliotecas
from scipy.fft import fft, ifft, fftshift
from scipy import integrate
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
import glob

#Parâmetros Gerais
L = 3
N = L*100
t_max = 120

dx = L/N

X = np.arange(0,L,dx)
K = 4*np.pi/L * np.arange(-L/2,L/2,dx)
K = fftshift(K)

#Forma diferencial da Equação KS
def KS(t,F,K=K):
  fourier = fft(F)
  return ifft(K**2 * fourier) - ifft(K**4 * fourier) - F/2 * ifft(K * 1j* fourier)

#Forma integral da Equação KS
def IKS(t,F,K=K):
  fourier = fft(F)
  return ifft(K**2 * fourier) - ifft(K**4 * fourier) - (ifft(K * 1j* fourier))**2

#Declaração das condições iniciais
F0 = np.sin(2*np.pi*X/L)**2 + 0j
plot = 1

V = []
T = []


#Solução por RK45
sol=integrate.RK45(KS,0,F0,t_max)

while sol.t < t_max:
  T.append(sol.t)
  V.append(sol.y)
  sol.step()


#Criação dos Frames
for i in range(len(T)//500):
  t = T[i*500]
  y = V[i*500]
  fig = plt.figure(figsize=(5,5))
  plt.plot(X,y.real,label='tempo:%.2f'% (t))
  plt.xlabel('X')
  plt.ylabel('v(x,t)')
  plt.legend(loc='upper right')
  plt.ylim(-5,5)
  fig.savefig('./grafs/%c.PNG'% (i+1))
  plt.close()


# Criação do GIF
frames = (Image.open(f) for f in sorted(glob.glob("./grafs/*.PNG")))
frame_one = next(frames)
frame_one.save("animado.gif", format="GIF", append_images=frames, save_all=True, duration=150, loop=0)



#Criação mapa de cores real
fig = plt.figure(figsize=(5,5))
graf = plt.pcolormesh(X,T,np.array(V).real,cmap="inferno",vmin=-5,vmax=5)
plt.xlabel('x')
plt.ylabel('t')
cbar = fig.colorbar(graf)
cbar.ax.set_title('v(x,t)')
fig.savefig("mapa_temporal.png")
plt.close()