Equação de Kuramoto–Sivashinsky: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 21: | Linha 21: | ||
Como esperado, a solução numérica teve sua estabilidade atrelada à suas condições iniciais; ou seja, a solução é instável (exceto em casos bem específicos, onde ela se comporta de forma análoga à equação da difusão). | Como esperado, a solução numérica teve sua estabilidade atrelada à suas condições iniciais; ou seja, a solução é instável (exceto em casos bem específicos, onde ela se comporta de forma análoga à equação da difusão). | ||
<center> | |||
{| | {| | ||
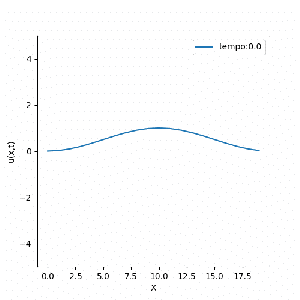
|[[Arquivo:FTCS_instavel.gif|thumb|upright=0.0|center|Solução FTCS de condição inicial <math>\sin{(\frac{\pi | |[[Arquivo:FTCS_instavel.gif|thumb|upright=0.0|center|Solução FTCS de condição inicial <math>\sin{\left( \frac{\pi}{20} x \right) }^2</math>|300px]] | ||
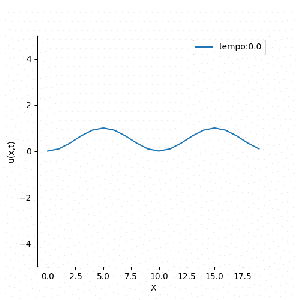
|[[Arquivo:FTCS_estavel.gif|thumb|upright=0.0|center|Solução FTCS de condição inicial <math>\sin{(\frac{\pi | |[[Arquivo:FTCS_estavel.gif|thumb|upright=0.0|center|Solução FTCS de condição inicial <math>\sin{\left( \frac{\pi}{10} x \right) }^2</math>|300px]] | ||
|} | |} | ||
</center> | |||
== Método Espectral (FFT) == | |||
Utilizando o método fft em conjunto com as propriedades da transformada de fourier, pode-se resolver a EDP utilizando a forma de derivada espectral. Esse método possui alta precisão e é capaz de incorporar o comportamento ondulatório de soluções, algo característico da equação de Kuramoto-Sivashinsky. | |||
A derivada espectral é caracterizada pela transformada de fourier de uma derivada, o que facilita a resolução de equações diferenciais parciais. | |||
<center><math> \mathcal{F} (v_x) = ik \mathcal{F} (v) \longrightarrow v_x = \mathcal{F^{-1}} \left( ik \mathcal{F} (v) \right) </math></center> | |||
Essa propriedade permite que a resolução da parte espacial da equação de Kuramoto-Sivashinsky diferencial seja dada por | |||
<center><math> v_t = \mathcal{F^{-1}} (k^2 \hat{v}) - \mathcal{F^{-1}} (k^4 \hat{v}) - \frac{ v \mathcal{F^{-1}} (ik \hat{v})}{2} </math></center>, | |||
onde <math> \hat{v} \equiv \mathcal{F} (v) </math>. A parte temporal também pode ser resolvida da mesma forma, mas o método de Runge-Kutta (RK45) foi aplicado em seu lugar por sua maior simplicidade e velocidade de processamento. | |||
Edição das 14h09min de 16 de dezembro de 2023
Nesta página apresentamos uma simulação de Dinâmica Molecular utilizando o potencial de Lennard-Jones como potencial de interação entre as partículas.
Equação
A equação de Kuramoto-Sivashinsky (KS) foi inicialmente proposta por Yoshiki Kuramoto e Gregory Sivashinsky para a modelagem das instabilidades da frente de uma chama laminar.
No entanto, a forma diferencial da equação foi descoberta independentemente na área de dinâmica de fluidos, onde ficou mais conhecida para a modelagem de filmes finos.
A equação apresenta comportamentos caóticos ao ser estudada em geometrias anelares, ou seja, condições de contorno periódicas; por isso esse será o caso estudado aqui.
Métodos de Solução
Diferenças Finitas (FTCS)
O método mais simples foi aplicado a fim de entender o comportamento da equação. Tentativas de linearização resultaram em uma equação de comportamento muito distinto do descrito na literatura; e portanto, não é de nosso interesse estudá-la. É importante relembrar que a aplicação do método FTCS não é recomendado no caso de não linearidades pois o método tem baixa precisão e pode acumular erros.
Como esperado, a solução numérica teve sua estabilidade atrelada à suas condições iniciais; ou seja, a solução é instável (exceto em casos bem específicos, onde ela se comporta de forma análoga à equação da difusão).
Método Espectral (FFT)
Utilizando o método fft em conjunto com as propriedades da transformada de fourier, pode-se resolver a EDP utilizando a forma de derivada espectral. Esse método possui alta precisão e é capaz de incorporar o comportamento ondulatório de soluções, algo característico da equação de Kuramoto-Sivashinsky.
A derivada espectral é caracterizada pela transformada de fourier de uma derivada, o que facilita a resolução de equações diferenciais parciais.
Essa propriedade permite que a resolução da parte espacial da equação de Kuramoto-Sivashinsky diferencial seja dada por
,
onde . A parte temporal também pode ser resolvida da mesma forma, mas o método de Runge-Kutta (RK45) foi aplicado em seu lugar por sua maior simplicidade e velocidade de processamento.