Equação de Kuramoto–Sivashinsky: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 23: | Linha 23: | ||
{| | {| | ||
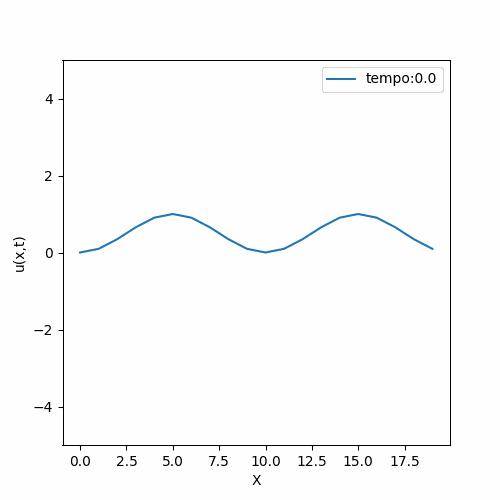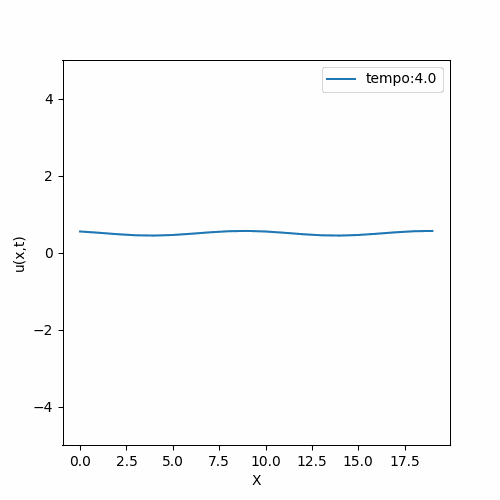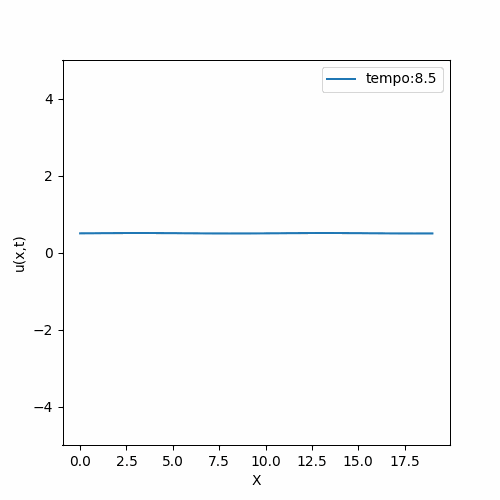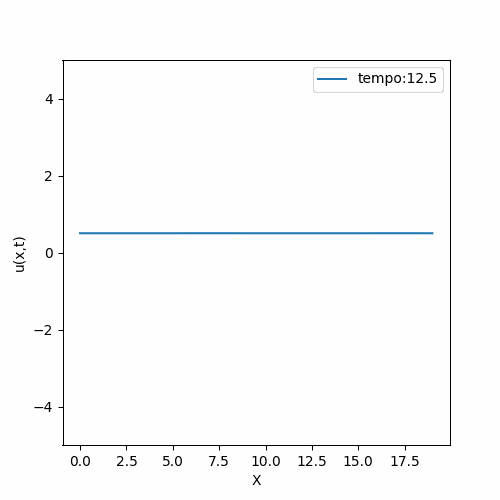
|[[Arquivo:FTCS_instavel.gif|thumb|upright=0.0|center|Solução FTCS de condição inicial <math>\sin{(\frac{\pi x}{20})}^2</math>|500px]] | |[[Arquivo:FTCS_instavel.gif|thumb|upright=0.0|center|Solução FTCS de condição inicial <math>\sin{(\frac{\pi x}{20})}^2</math>|500px]] | ||
|[[Arquivo:FTCS_estavel.gif|thumb|upright=0.0|center|Solução FTCS de condição inicial <math>\sin{(\frac{\pi x}{ | |[[Arquivo:FTCS_estavel.gif|thumb|upright=0.0|center|Solução FTCS de condição inicial <math>\sin{(\frac{\pi x}{10})}^2</math>|500px]] | ||
|} | |} | ||
Edição das 12h19min de 16 de dezembro de 2023
Nesta página apresentamos uma simulação de Dinâmica Molecular utilizando o potencial de Lennard-Jones como potencial de interação entre as partículas.
Equação
A equação de Kuramoto-Sivashinsky (KS) foi inicialmente proposta por Yoshiki Kuramoto e Gregory Sivashinsky para a modelagem das instabilidades da frente de uma chama laminar.
No entanto, a forma diferencial da equação foi descoberta independentemente na área de dinâmica de fluidos, onde ficou mais conhecida para a modelagem de filmes finos.
A equação apresenta comportamentos caóticos ao ser estudada em geometrias anelares, ou seja, condições de contorno periódicas; por isso esse será o caso estudado aqui.
Métodos de Solução
Diferenças Finitas (FTCS)
O método mais simples foi aplicado a fim de entender o comportamento da equação. Tentativas de linearização resultaram em uma equação de comportamento muito distinto do descrito na literatura; e portanto, não é de nosso interesse estudá-la. É importante relembrar que a aplicação do método FTCS não é recomendado no caso de não linearidades pois o método tem baixa precisão e pode acumular erros.
Como esperado, a solução numérica teve sua estabilidade atrelada à suas condições iniciais; ou seja, a solução é instável (exceto em casos bem específicos, onde ela se comporta de forma análoga à equação da difusão).