Modelo de Blume-Capel bidimensional

Modelo de Ising

No contexto de transições de fase ferromagnéticas, um modelo muito simples, mas não trivial, que incorpora interações de curto alcance (vizinhos próximos) é o Modelo de Ising. Proposto em 1925 pelo físico alemão alemão Ernst Ising (1900-1998), possui o seguinte formato:

${\mathcal {H}}=-J\sum _{<i,j>}\sigma _{i}\sigma _{j}-H\sum _{i=1}^{N}\sigma _{i},$

onde $\sigma _{i}$ é uma variável aleatória que pode assumir os valores $\pm 1$ nos sítios $i=1,2,...,N$ de uma rede cristalina. O primeiro termo da soma, referente aos vizinhos próximos <i,j>, representa as energias de interação que devem dar origem a um estado ferromagnético (se J>0). Já o segundo termo, que representa a interação do sistema com um campo magnético externo H, é de caráter puramente paramagnético.

Pode-se interpretar as variáveis de spin de diferentes maneiras:

1.Componentes do spin dos átomos, na direção do campo externo, que podem "apontar para cima ou para baixo";
2.Como uma indicação de que o sítio i pode estar ocupado por um átomo de tipo A ou B;
3.Como um número de ocupação, que assinala a presença ou a ausência de uma molécula numa determinada célula de um "gás de rede".

A multiplicidade de interpretações permite inferir o caráter universal do modelo. Trata-se de um excelente ponto de partida para o estudo de modelos mais sofisticados.

A solução analítica, conforme demonstrado por Ising em 1925 para o caso unidimensional, passa inevitavelmente pelo cálculo da função de partição canônica,

$Z_{N}=\sum _{\sigma _{i}}exp(-\beta {\mathcal {H}}),$

cuja soma abrange todas as $2^{N}$ configurações. Na equação acima, $\beta ={\frac {1}{k_{b}T}}$. Para fins de simplificação, foi feita a suposição de que $k_{b}=1$.

No equilíbrio termodinâmico, a uma temperatura T, a probabilidade $P(\sigma )$ de encontrar o sistema na configuração $\sigma$ é

$P(\sigma )={\frac {1}{Z}}e^{-\beta E(\sigma )}.$

Outra função de estado particularmente relevante é a magnetização total, dada pela relação

${\mathcal {M}}=\sum _{i}\sigma _{i}.$

Já a energia do sistema, bem como as variações desta, é calculada, naturalmente, através do hamiltoniano que descreve o modelo de Ising.

Modelo de Blume-Capel

O modelo de Blume-Capel, batizado em honra aos proponentes Martin Blume (1932-2021) e Hans Willelm Capel (1936-), é uma generalização do modelo de Ising na medida em que agora os spins podem se alinhar paralelamente, antiparalelamente e ortogonalmente. Em outras palavras, o modelo de Blume-Capel trata do caso de um sistema de partículas com spin s=1, com as três configurações possíveis (-1, 0, +1), ao passo que o modelo de Ising tratava do caso em que $s={\frac {1}{2}}$, com somente duas configurações possíveis (-1,+1). Matematicamente:

${\mathcal {H}}=-J\sum _{<i,j>}\sigma _{i}\sigma _{j}+D\sum _{i}\sigma _{i}^{2},$

onde D representa a anisotropia do sistema. No caso limite em que D=0, recupera-se os resultados do modelo de Ising.

Para o cálculo da magnetização e energia do sistema, o raciocínio é o mesmo aplicado ao modelo de Ising, com a diferença de que agora deve-se levar em conta o termo quadrático bem como o fator D.

Por fim, é interessante citar uma peculiaridade deste modelo, o chamado ponto tricrítico. Trata-se de uma singularidade no diagrama de fase caracterizada por uma temperatura crítica $T_{c}$, que de acordo ...., é da ordem de $T_{c}=0.69$. A análise realizada neste trabalho não contemplou tal fenômeno, mas trata-se de uma possibilidade para um eventual prosseguimento da atividade.

Método de Monte Carlo

Neste trabalho utilizou-se o método de Monte Carlo, muito eficaz para obter o comportamento de sistemas magnéticos. Grosso modo, a ideia do método de Monte Carlo é escolher uma sequência de configurações independentes, constituindo uma cadeia de Markov. Algumas configurações iniciais são geradas longe do equilíbrio, mas à medida que o tempo passa devem ser geradas muitas configurações típicas de equilíbrio, a partir das quais pode-se realizar uma média aritmética, por exemplo. Pelo fato do referido método ter sido utilizado inúmeras vezes em trabalhos anteriores, julgou-se que apresentar uma abordagem teórica mais aprofundada soaria demasiado repetitivo.

No subtópico a seguir, realizou-se uma breve discussão acerca da implementação do Algoritmo de Metrópolis.

Algoritmo de Metropolis

Neste trabaho utilizou-se o Algoritmo de Metropolis, bastante discutido em atividades anteriores, para obter os dados do comportamento dos observáveis do sistema. Os passos para implementação do algoritmo:

1. Escolher uma condição inicial, e.g, aleatória;
2. Calcular a energia correspondente à configuração escolhida;
3. Escolher um sítio da rede e propôr uma nova direção para o seu spin;
4. Calcular a energia do estado recém gerado bem como a diferença energética $\Delta E$;
5. Se $\Delta E$ for negativo, aceitar a nova configuração gerada;
6. Se $\Delta E$ for positivo, calcular $e^{-\beta \Delta E}$ e sortear um número aleatório, r, entre 0 e 1:
 6.1) Se $r<e^{-\beta \Delta E}$, aceitar a nova configuração;
 6.2) Se $r>e^{-\beta \Delta E}$, continuar com a configuração inicial;	
7. Voltar ao item 3 e repetir o procedimento.

Resultados

Em função do tempo [MCS]

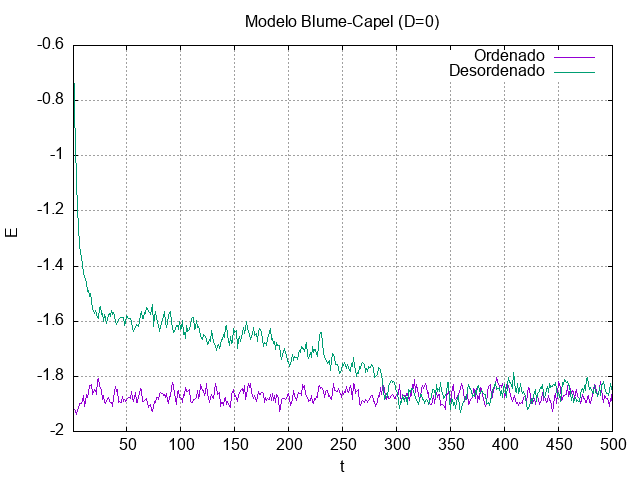
T=1.1

Energia vs tempo para uma temperatura fixa T=1.1

No gráfico acima, observa-se o comportamento da energia do em função do tempo. Para o sistema inicializado de forma desordenada, na forma de uma matriz L x L, onde L=32, a energia inicial da amostra é da ordem de -0.7. O sistema converge para a menor energia possível, mas isso só ocorre após a chamada termalização, ou seja, após uma determinada quantidade de passos temporais (na ordem de 300). Em outras palavras, é necessário que os componentes do sistema interajam de modo a atingirem a configuração de energia minimizada. Dessa forma, observa-se que em uma cadeia temporal relativamente curta, todos os spins são flipados e atingem a sua configuração menos energética.

O caso ordenado, onde o sistema foi inicializado com todos os spins para baixo, apresenta uma energia que flutua ao redor da energia inicial (menor) do sistema.

Magnetização vs tempo para uma temperatura fixa T=1.1

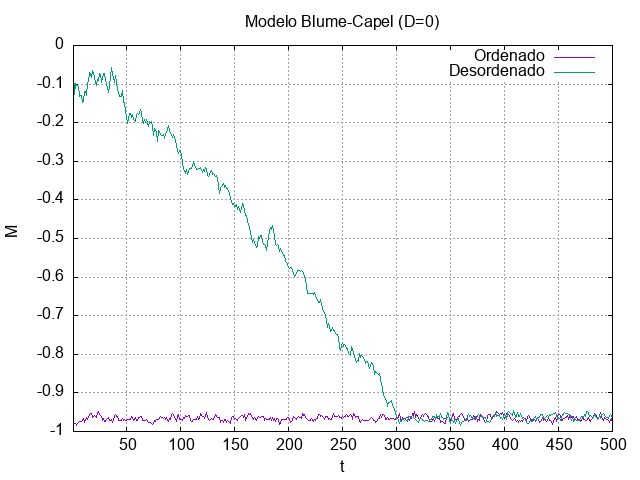
No gráfico acima, observa-se que o sistema inicializado de forma aleatória possui uma magnetização inicial muito próxima de zero, o que faz sentido físico tendo em vista a aleatoriedade da distribuição dos spins. A convergência para o caso ordenado demora o mesmo número de passos, 300, que no caso energético, o que era esperado.

No caso ordenado, a magnetização flutua ao redor do valor inicial de -1 durante a realização da simulação.

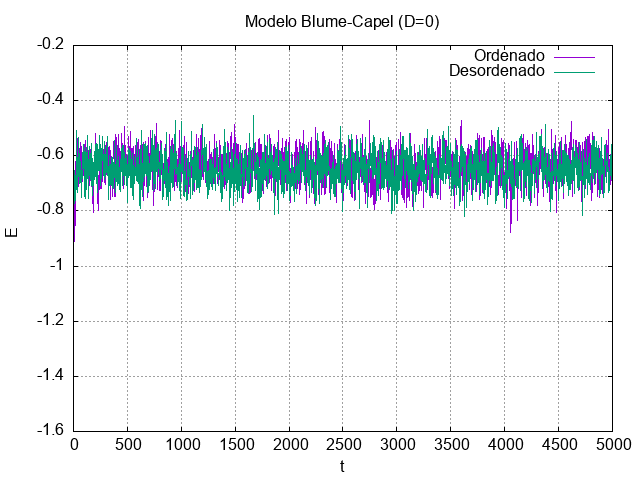
T=2.1

Energia vs tempo para uma temperatura fixa T=2.1

Diferentemente do caso T=1.1, agora o comportamento energético denota que tanto o sistema inicializado de forma ordenada quanto desordenada convergem rapidamente (em poucos passos temporais) para um valor central de energia, em torno de -0.7. Isso se deve à maior temperatura de inicialização do sistema, o que implica uma maior desordem configuracional. No decorrer da simulação, a energia flutua ao redor do referido valor central.

Magnetização vs tempo para uma temperatura fixa T=2.1

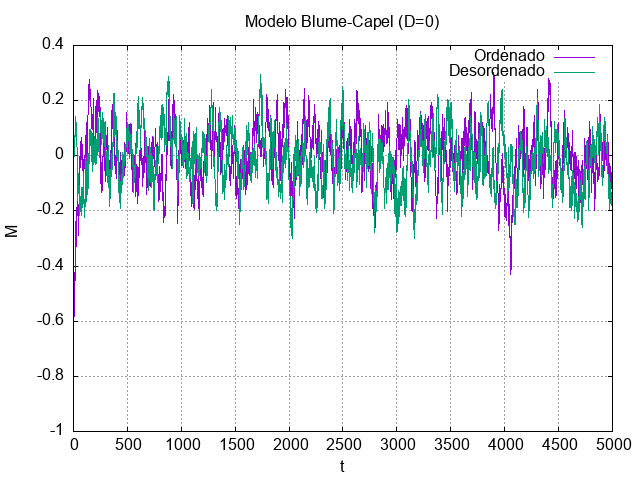
Diferentemente do caso energético, a magnetização se descorrelaciona mais devagar, levando quase 50 passos temporais para tanto. No decorrer da simulação, a magnetização flutua ao redor de 0.

Em função da temperatura

Energia vs Temperatura, para diferentes tamanhos do sistema.

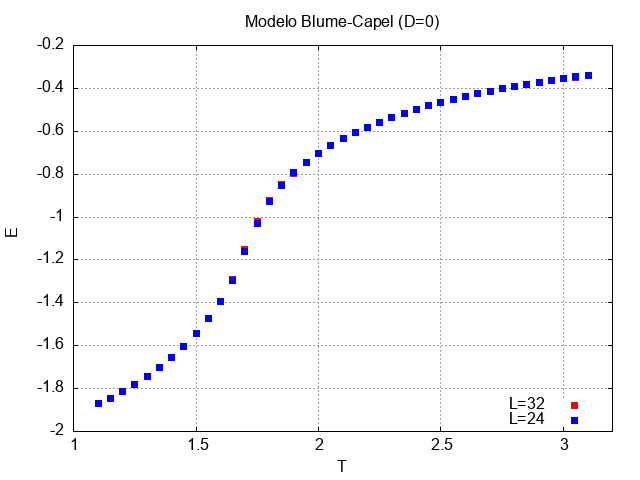
O gráfico acima apresenta o comportamento energético de um sistema 24 x 24 e outro de 32 x 32. Os valores plotados representam o somatório das energias de cada configuração dividido pelo fator $L^{2}$. Não faz sentido, no presente caso, pensar em inicialização aleatória ou ordenada visto que o valor plotado representa uma média dos valores de energia após 10000 interações. Em outras palavras, a média é tirada quando o sistema já está em equilíbrio, por assim dizer.

Para ambos os casos, o comportamento energético é praticamente idêntico: por se tratar de D=0, isso emula o comportamento observado no modelo de Ising.

Magnetização vs Temperatura, para diferentes tamanhos do sistema.

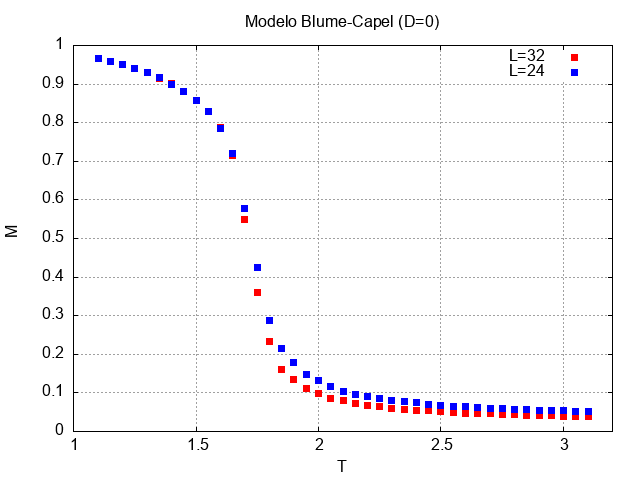
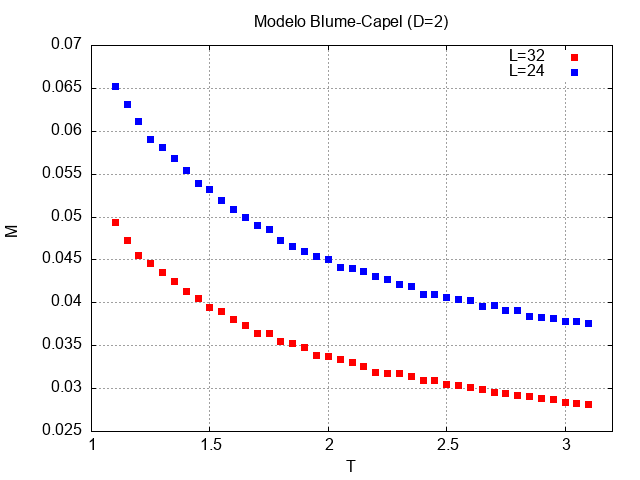
Para o caso da magnetização em função da temperatura, é interessante notar que foi plotado o somatório dos módulos das magnetizações de cada sítio, sendo novamente esse valor dovidido por $L^{2}$.

Inicialmente a magnetização de ambos os sistemas apresentava o mesmo comportamento. Conforme a temperatura aumentava, no entanto, a magnetização do sistema de L=32 diminuía mais rapidamente, até que por volta de T=2.5, ambos os comportamentos voltavam a se igualar. Novamente, isso confirma o resultado do modelo de Ising.

Energia vs Temperatura, para diferentes tamanhos do sistema.

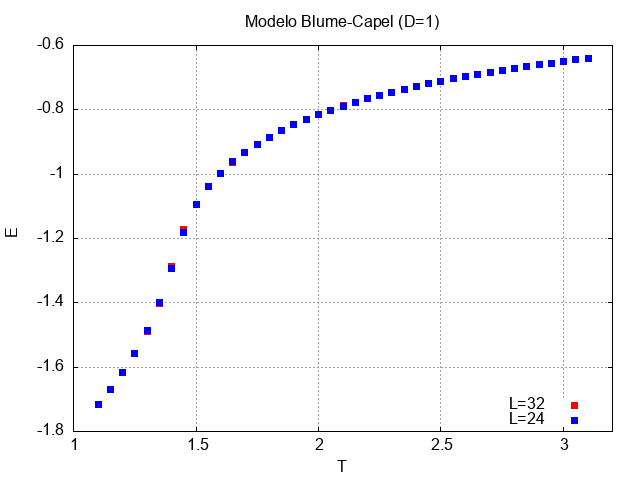
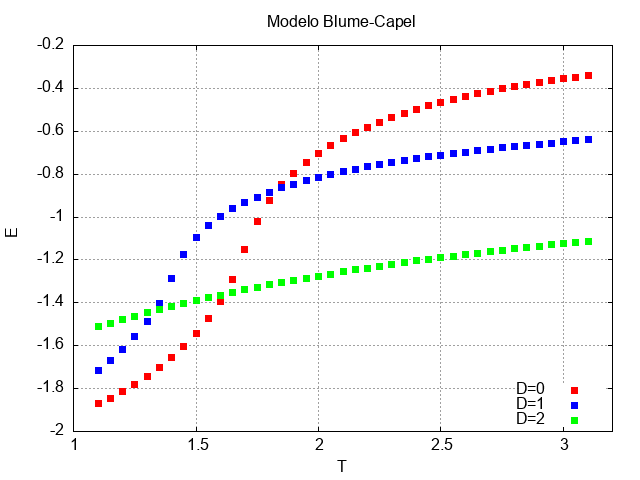
O gráfico acima descreve um comportamento semelhante àquele observado quando D=0: ambos os sistema sapreesentam um comportamento energético quase idêntico.

Magnetização vs Temperatura, para diferentes tamanhos do sistema.

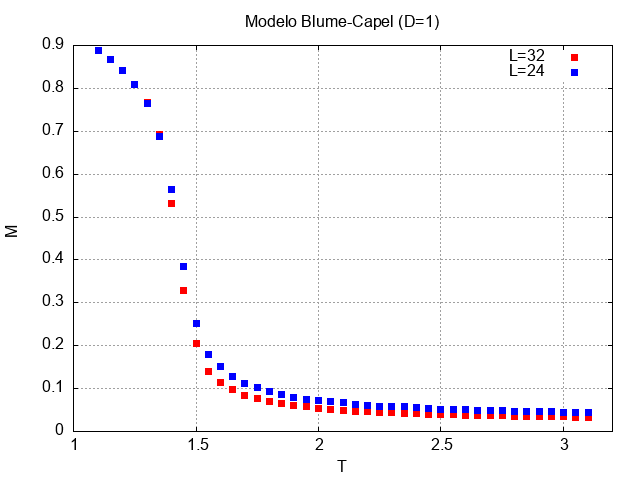
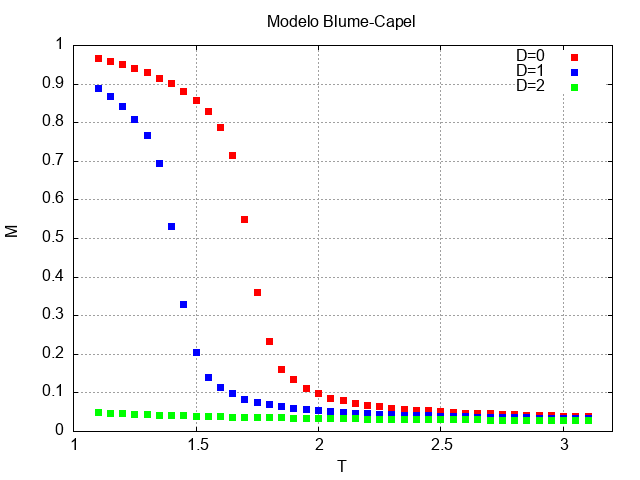
Novamente observa-se um comportamento semelhante àquele obtido no caso D=0. Agora, no entanto, as magnetizações dos dois sistemas distintos passam a apresentar o mesmo comportamento a partir de uma temperatura maior, em torno de T=2,5.

Energia vs Temperatura, para diferentes tamanhos do sistema.

É interessante notar que, no presente caso, as magnetizaçãos são praticamente idênticas e quase nulas.

Magnetização vs Temperatura, para diferentes tamanhos do sistema.

É interessante notar que, no presente caso, as magnetizaçãos são muito semelhantes, ambas muito próximas do valor nulo. Isso se deve ao fato da constate D, para este caso, ser igual a dois.

Energia vs Temperatura, para diferentes valores de D e L=32.

Mgnetização vs Temperatura, para diferentes valores de D e L=32.

Considerações Finais

Neste trabalho foi realizada uma análise do modelo de Blume-Capel bidimensional, variando-se o parâmetro anisotrópico (D) e a energia do sistema. Obteve-se resultados interessantes na medida em que vieram de encontro ao comportamento fisicamente esperado, e.g., diminuição da magnetização com aumento da temperatura, diferentes evoluções de sistemas inicializados heterogeneamente, dentre outros. Apesar dos resultados obtidos, não foi possível, tendo em vista o limitado escopo inicial da atividade, observar o fenômeno do ponto tricrítico: para tanto seria necessário construir um diagrama de fase do sistema, tarefa que demandaria muito mais esforço e tempo, tendo sido este último fator o maior impeditivo para a realização do intento.

Nesse contexto, há de se salientar que, de acordo com a literatura consultada, a temperatura crítica do sistema é da ordem de 0,69. Tendo em vista que o Algoritmo de Metropolis apresenta problemas para lidar com um sistema em baixas temperaturas, seria necessário implementar uma outra abordagem, e.g., mudar o algoritmo ou implementar um híbrido entre o Metropolis e algum outro método conveniente. Trata-se de uma motivação para um futuro prosseguimento do trabalho desenvolvido.

Referências Bibliográficas

Salinas, Sílvio R. A., Introdução à Física Estatística. São Paulo: Editora da Universidade de São Paulo, Brasil, 2ª ed., 2013.

M. E. J. Newman, G. T. Barkema, Monte Carlo Methods in Statistical Physics. Oxford University Press Inc., New York, 1999.

Hu, Wenjian e Singh, Rajiv R.P. e Scalettar, Richar T. Discovering phases, phase transitions, and crossovers through unsupervised machine learning: A critical examination. Phys. Rev. E, 95, 6, 14, Jun, 2017. Disponível em: https://link.aps.org/doi/10.1103/PhysRevE.95.062122

Códigos

Blume_Capel

Agradecimentos

Ao professor Heitor Fernandes, por gentilmente ter disponibilizado um de seus códigos - que serviu de base para a realização do presente estudo -, pela paciência em sanar dúvidas e auxiliar no que fosse preciso.