|
|
| Linha 3: |
Linha 3: |
| | | |
| O objetivo deste trabalho é aplicar o Shooting method (método do chute) para encontrar as primeiras funções de onda espaciais da Equação de Schrödinger para o caso do poço de potencial infinito. Após, será realizada a evolução temporal através do Método de Crank-Nicolson. | | O objetivo deste trabalho é aplicar o Shooting method (método do chute) para encontrar as primeiras funções de onda espaciais da Equação de Schrödinger para o caso do poço de potencial infinito. Após, será realizada a evolução temporal através do Método de Crank-Nicolson. |
|
| |
| ==Shooting Method==
| |
| Muitos métodos numéricos (e.g. Runge-Kutta, Forward Euler) requerem os valores da função e de sua derivada no ponto inicial. Acontece que podem haver problemas em que estes valores não estarão disponíveis, principalmente o valor da derivada em questão. Uma alternativa seria conjecturar o valor da condição inicial e integrar, através de um método apropriado, em direção à outra condição de contorno: um "chute" apropriado faria com que a integração evoluísse e retornasse um valor muito próximo, a depender da acurácia necessária, ao da condição de contorno. A ideia seria executar os seguintes passos:
| |
|
| |
| # Supor um valor para a condição de contorno desconhecida (e.g. <math>y(0)</math> ou <math>y'(0)</math>);
| |
| # Integrar o problema através de um método conhecido até a próxima condição de contorno (e.g., <math>y(L)</math>);
| |
| # Se o chute inicial não fez com que o sistema evoluísse até <math>y(L)</math>, então deve-se supor outro valor para a condição inicial e repetir o procedimento.
| |
|
| |
| O método descrito acima de forma simplificada recebe o nome, em inglês, de ''Shooting method'', o que em português seria algo como "Método do tiro" ou "Método do chute". Na próxima seção esse método será aplicado para o caso do poço infinito de potencial.
| |
|
| |
| ===Poço de potencial infinito===
| |
| Seja a equação <math>\frac{d^2\psi}{dx^2}=-k\psi E</math>, onde <math>k=\frac{2m}{\hbar^2}</math>.
| |
|
| |
| Escrevendo com outra notação: <math>\ddot{\psi}=-k\psi E</math>.
| |
|
| |
| Dividindo o problema em <math>\Delta x </math>'s pequenos, pode-se reescrever a equação acima da seguinte forma:
| |
|
| |
| <center><math> \ddot{\psi}=\frac{\Delta \dot{\psi}}{\Delta x}=\frac{\dot{\psi_2}-\dot{\psi_1}}{\Delta x} \implies \dot{\psi_2}=\ddot{\psi} \Delta x + \dot{\psi_1}</math></center>.
| |
|
| |
| Também:
| |
| <center><math>\dot{\psi}=\frac{\Delta \psi}{\Delta x}=\frac{\psi_2-\psi_1}{\Delta x} \implies \psi_2 = \dot{\psi}\Delta x + \psi_1</math></center>.
| |
|
| |
| Além disso:
| |
| <center><math>\Delta x = x_2-x_1 \implies x_2 = x_1 +\Delta{x}</math></center>.
| |
|
| |
| A integração, então, é realizada utilizando as relações 8, 9, 10 e 11, até que se atinja a borda do poço, isto é, <math>x=L</math>.
| |
|
| |
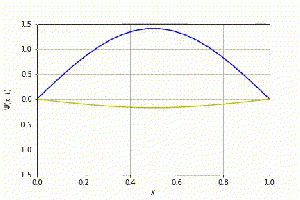
| Com a discretização acima, foi possível implementar o algoritmo. Das condições de contorno do problema, sabe-se que <math>\psi(0)=0</math>, de modo que <math>\psi_1=0</math>. No entanto, o valor da derivada <math>\dot{\psi_1}</math> não é conhecido, de modo que supõe-se que seja uma constante, a saber, <math>\dot{\psi_1}=1</math>. Chutando que <math>E=0</math>, utilizando a massa do elétron e <math>L=1</math>, obtém-se a primeira solução estacionária:
| |
| [[Arquivo:n=1.png|300px|thumb|center|Solução estacionária (n=1)]]
| |
| Pode-se observar que o valor de energia obtido numericamente é cerca de 4% menor do que aquele obtido analiticamente.
| |
|
| |
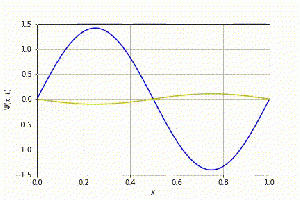
| Para o caso n=2:
| |
| [[Arquivo:n=2.png|300px|thumb|center|Solução estacionária (n=2)]]
| |
| Aqui, o valor obtido numericamente é aproximadamente 5% maior do que o valor obtido analiticamente.
| |
|
| |
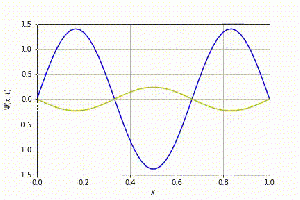
| Para o caso n=3:
| |
| [[Arquivo:n=3.png|300px|thumb|center|Solução estacionária (n=3)]]
| |
| Para este caso, o valor numérico é cerca de 1% menor do que o valor analítico.
| |
|
| |
|
| ==Método de Crank-Nicolson== | | ==Método de Crank-Nicolson== |
Edição das 19h28min de 12 de fevereiro de 2023
O objetivo deste trabalho é aplicar o Shooting method (método do chute) para encontrar as primeiras funções de onda espaciais da Equação de Schrödinger para o caso do poço de potencial infinito. Após, será realizada a evolução temporal através do Método de Crank-Nicolson.
Método de Crank-Nicolson
Seja a equação diferencial
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial f}{\partial t}=L_1{\textbf{r}}f(\textbf{r},t)}
,
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{\textbf{r}}}
é um operador diferencial linear em r.
Em forma discretizada no tempo, pode-se escrever
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^{n+1}(\textbf{r})-f^{n}(\textbf{r})= L_{\textbf{r}}f^{n}(\textbf{r})dt }
.
Por simetria, pode-se escrever a equação acima utilizando um f à direita:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^{n+1}(\textbf{r})-f^{n}(\textbf{r})= L_{\textbf{r}}f^{n+1}(\textbf{r})dt . }
A equação acima é dita "explícita" pois, para o cálculo de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^{n+1}}
, só é utilizado o valor já explicitamente calculado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^{n}}
. Já a equação anterior é chamada implícita pois Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^{n+1}}
está presente explicitamente. Em termos numéricos, um método peca pelo excesso enquanto o outro o faz pela falta, de modo que um resultado mais satisfatório pode ser obtido ao tomar-se a média dos dois:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^{n+1}(\textbf{r})-f^{n}(\textbf{r})=\frac{dt}{2}(L_{\textbf{r}}f^{n+1}(\textbf{r})+L_{\textbf{r}}f^n(\textbf{r})). }
Após alguma álgebra:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^{n+1}(\textbf{r})=\left(1-\frac{dt}{2}L_{\textbf{r}}\right)^{-1}\left(1+\frac{dt}{2}L_{\textbf{r}}\right)f^{n}(\textbf{r}) }
.
Chamando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle M=I+\frac{dt}{2}L_{\textbf{r}} }
e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=I-\frac{dt}{2}L_{\textbf{r}} }
, onde I indica a matriz identidade, pode-se reescrever a equação acima na seguinte maneira:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^{n+1}=E^{-1}Mf^{n} }
.
Trata-se do método de Crank-Nicolson, mais estável e preciso do que os métodos implícito e explícito. Caso o problema apresentar condições de contorno, estas serão devidamente implementadas nos elementos das matrizes M e E.
Equação de Schrödinger
Seja a equação de Schrödinger unidimensional
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial\Psi}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^2 \Psi}{\partial x^2}+V\Psi }
.
Efetuando a discretização das variáveis através do Método de Crank-Nicolson, obtém-se:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial \Psi}{\partial t}= \frac{\Psi_{j}^{n+1}-\Psi_{j}^{n}}{\Delta t} ;}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\hbar^2}{2m}\frac{\partial^2 \Psi}{\partial x^2} = \frac{\hbar^2}{2m}\left[\frac{(\Psi_{j+1}^{n+1}-2\Psi_{j}^{n+1}+\Psi_{j-1}^{n+1})+ (\Psi_{j+1}^{n}-2\Psi_{j}^{n}+\Psi_{j-1}^{n})}{2\Delta x^2}\right] ;}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\Psi = \frac{1}{2}[V_{j}^{n+1}\Psi_{j}^{n+1}+V_{j}^{n}\Psi_{j}^{n}] .}
Substituindo as discretizações na eq. de Schrödinger:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\left(\frac{\Psi_{j}^{n+1}-\Psi_{j}^{n}}{\Delta t}\right)=-\frac{\hbar^2}{4m(\Delta x)^2} \left[(\Psi_{j+1}^{n+1}-2\Psi_{j}^{n+1}+\Psi_{j-1}^{n+1})+ (\Psi_{j+1}^{n}-2\Psi_{j}^{n}+\Psi_{j-1}^{n})\right]+\frac{1}{2}[V_{j}^{n+1}\Psi_{j}^{n+1}+V_{j}^{n}\Psi_{j}^{n}].}
Supondo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar=m=1}
e separando as partes explícita e implícita, obtém-se, após alguma álgebra:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi_{j}^{n+1}\left[1+\frac{i\Delta t}{2}\left(\frac{1}{\Delta x^2}+V_{j}^{n+1}\right)\right]+\Psi_{j-1}^{n+1}\left[-\frac{i\Delta t}{4\Delta x^2}\right]+\Psi_{j+1}^{n+1}\left[-\frac{i\Delta t}{4\Delta x^2}\right] = \Psi_{j}^{n}\left[1-\frac{i\Delta t}{2}\left(\frac{1}{\Delta x^2}+V_{j}^{n}\right)\right]+\Psi_{j-1}^{n}\left[-\frac{i\Delta t}{4\Delta x^2}\right]+\Psi_{j+1}^{n}\left[\frac{i\Delta t}{4\Delta x^2}\right].}
Definindo
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a\equiv\frac{-i\Delta t}{4(\Delta x)^2}}
e
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_{j}\equiv\left(1+\frac{i\Delta t}{2}\right)\left(\frac{1}{\Delta x^2}+V_j\right),}
obtém-se:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi_{j}^{n+1}b_{j}+\Psi_{j-1}^{n+1}a+\Psi_{j+1}^{n+1}a = \Psi_{j}^{n}b_{j}^{*}+\Psi_{j-1}^{n}a^{*}+\Psi_{j+1}^{n}a^{*} .}
A equação acima pode ser escrita em forma matricial, de modo que:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{C}\Psi^{n+1}=\hat{D}\Psi^{n},}
onde
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{C} = \begin{bmatrix} b _{0} &a &0 & &... &0 \\ a & b_{1} &a &0 &... &0\\ 0 & a &b_{2} &a & 0 &0 \\ 0 & 0 & \ddots & \ddots &\ddots \\ ... & ... &... & a &b_{j-1} &a \\ 0 & 0 &... & 0 &a &b_{j}\\ \end{bmatrix} }
e
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{D} = \begin{bmatrix} b_{0}^{*} &a &0 & &... &0 \\ a^{*} & b_{1}^{*} &a^{*} &0 &... &0\\ 0 & a^{*} &b_{2}^{*} &a^{*} & 0 &0 \\ 0 & 0 & \ddots & \ddots &\ddots \\ ... &... &... & a^{*} &b_{j-1}^{*} &a^{*} \\ 0 & 0 &... & 0 &a^{*} &b_{j}^{*}\\ \end{bmatrix} }
Para avaliar a evolução temporal do sistema, é necessário encontrar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi^{n+1}}
. Utilizando resultados anteriores, pode-se obter Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi^{n+1}}
através da seguinte relação:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi^{n+1}=\hat{C}^{-1}\hat{C^{*}}\Psi^{n} }
Poço de potencial infinito
Para o presente caso a ideia é obter a evolução temporal do sistema, impondo condições de contorno iguais a zero, de modo que os operadores Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{C}}
e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{D}}
ficam:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{C} = \begin{bmatrix} 1 &0 &0 & &... &0 \\ a & b &a &0 &... &0\\ 0 & a &b &a & 0 &0 \\ 0 & 0 & \ddots & \ddots &\ddots \\ ... &... &... & a &b &a \\ 0 & 0 &... & 0 &0 &1\\ \end{bmatrix} }
e
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{D} = \begin{bmatrix} 1 &0 &0 & &... &0 \\ a^{*} & b^{*} &a^{*} &0 &0... &0\\ 0 & a^{*} &b^{*} &a^{*} & 0 &0 \\ 0 & 0 & \ddots & \ddots &\ddots \\ ... &... &... & a^{*} &b^{*} &a^{*} \\ 0 & 0 &... & 0 &0 &1\\ \end{bmatrix} }
A ideia é que o primeiro e o último termo do tanto do vetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi^{n}}
quanto do vetor Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi^{n+1}}
seja constante, o que satisfaz as condições de contorno do presente caso. Também é interessante notar que os índices Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle b}
são todos constantes, visto que no presente caso o potencial dentro do poço é nulo.
Implementando o algoritmo descrito acima, obteve-se:
Evolução temporal para o caso n=1. Nesta animação e nas subsequentes, foram sobrepostas as partes real e imaginária da equação de Schrödinger: a linha azul diz respeito à parte real enquanto a amarela, à imaginária.
Na figura acima, tem-se a evolução do caso n=2.
Por último, o caso n=3.