Equação de Langevin: mudanças entre as edições
Sem resumo de edição |
|||
| Linha 76: | Linha 76: | ||
É importante lembrar que entre os dois últimos passos é necessário atualizar o termo <math>\vec{f}</math>, já que ele pode depender de termos já atualizados como <math>\vec{p}</math> ou <math>\vec{r}</math>. | É importante lembrar que entre os dois últimos passos é necessário atualizar o termo <math>\vec{f}</math>, já que ele pode depender de termos já atualizados como <math>\vec{p}</math> ou <math>\vec{r}</math>. | ||
== Implementação == | |||
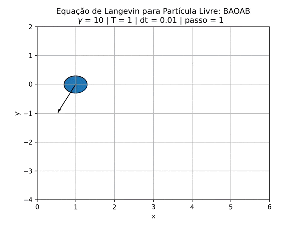
[[Arquivo:Livre_g10T1_c.gif|thumb|center|300px|Simulação de uma partícula livre sob o efeito da Equação de Langevin.]] | |||
=== Referências === | === Referências === | ||
<references/> | <references/> | ||
Edição das 16h13min de 17 de outubro de 2022
Artur Uhlik Fröhlich e Leonardo Dasso Migotto
O objetivo deste trabalho é resolver computacionalmente a equação de Langevin utilizando o método BAOAB[LEIMKUHLER.] Serão explorados os casos de partículas individuais livres ou sujeitas a um campo potencial, estudando os efeitos da variação do coeficiente de atrito no desvio quadrático médio e na transisão de fases.
Equação de Langevin
Esta equação diferencial estocástica descreve a evolução de um sistema quando sujeito a forças do tipo determinísticas e estocásticas simultâneamente. A sua aplicação mais popular é relativa ao movimento Browniano, o movimento de uma partícula macroscópica imersa em um fluído, sujeita à força de atrito excercida pelas partículas microscópicas do fluído. Neste caso, a equação pode ser escrita como:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\vec{v}}{dt} = -\gamma \vec{v}/m + \Epsilon (t). }
Na equação acima, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} é o coeficiente de atrito e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Epsilon(t)} é um ruído estocástico branco, que segue o Teorema Central do Limite com média 0 e desvio padrão relacionado à temperatura, a Constante de Boltzmann, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} e a massa da partícula. A partir desta expressão, é possível descobrir a relação do coeficiente de difusão do fluído e os valores envolvidos na equação:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D = \frac{2k_{B}T}{\gamma m} }
Onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} é o coeficiente de difusão do meio, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B} é a constante de Boltzmann, Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} é a temperatura e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} é a massa da partícula macroscópica. Outra relação presente no livro do Frenkel [FRENKEL], desenvolvida teoricamente, é a do coeficiente de difusão e o deslocamento quadrático médio de uma partícula no meio:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \langle \left( r(t) - r_0(t) \right)^2 \right \rangle = 2dDt }
Método BAOAB
O método numérico escolhido para realizar a integração da equação é conhecido como BAOAB, desenvolvido por Leimkuhler e Mattews [1] utilizado para resolver equações diferenciais estocásticas.
Ele é baseado na solução exata para o momentum,
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\vec{p} = -\gamma \vec{p}dt + \sqrt{2\gamma mk_{B}T}d\vec{W} , }
e faz o uso de um método de separação das equações entre as denominadas A, B e O, respectivamente representadas:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}\left(t+\frac{\Delta t}{2}\right) = \vec{r}(t) +\frac{\Delta t}{2}\vec{p}\left ( t +\frac{\Delta t}{2}\right )\frac{1}{m} }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{p}\left(t + \frac{\Delta t}{2}\right) = \vec{p}(t) + \frac{\Delta t}{2}\vec{f}(t) }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{p'}\left(t + \frac{\Delta t}{2}\right) = exp(-\gamma \Delta t)\vec{p}\left(t + \frac{\Delta t}{2}\right) + \sqrt{1-exp(-2\gamma \Delta t)}\sqrt{mk_{B}T}\vec{G} }
O Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{G}} aqui representa um número aleatório Gaussiano que faz o papel da força estocástica.
A equação "A" realiza meio passo no tempo da distância, a "B" realiza um meio passo para o momentum e o "O" contabiliza a contribuição estocástica equação.
Essas equações podem formar vários algoritmos de integração mas o utilizado nesse trabalho será o BAOAB:
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{p}\left(t + \frac{\Delta t}{2}\right) = \vec{p}(t) + \frac{\Delta t}{2}\vec{f}(t) \quad (1) }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}\left(t+\frac{\Delta t}{2}\right) = \vec{r}(t) +\frac{\Delta t}{2}\vec{p}\left ( t +\frac{\Delta t}{2}\right )\frac{1}{m} \quad (2) }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{p'}\left(t + \frac{\Delta t}{2}\right) = exp(-\gamma \Delta t)\vec{p}\left(t + \frac{\Delta t}{2}\right) + \sqrt{1-exp(-2\gamma \Delta t)}\sqrt{mk_{B}T}\vec{G} \quad (3) }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}(t + \Delta t) = \vec{r}\left(t + \frac{\Delta t}{2}\right) +\frac{\Delta t}{2}\vec{p'}\left ( t +\frac{\Delta t}{2}\right )\frac{1}{m} \quad (4) }
- Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{p}(t + \Delta t) = \vec{p'}\left(t + \frac{\Delta t}{2}\right) + \frac{\Delta t}{2}\vec{f}(t) \quad (5) }
É importante lembrar que entre os dois últimos passos é necessário atualizar o termo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{f}} , já que ele pode depender de termos já atualizados como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{p}} ou Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}} .
Implementação
Referências
- ↑ Leimkuhler, B., & Matthews, C. (2015). Molecular Dynamics: With Deterministic and Stochastic Numerical Methods. (Interdisciplinary Applied Mathematics; Vol. 39). Springer. https://doi.org/10.1007/978-3-319-16375-8