Modelos Epidemiológicos

Em construção

Grupo: Gabriel Schmökel, Julia Remus e Luis Gustavo Lang Gaiato

O objetivo do trabalho é realizar a implementação do modelo SIR e de um modelo simplificado do proposto pelo artigo "An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics" utilizando Monte Carlo.

Será apresentada uma breve introdução sobre o tema e as equações que envolvem o desenvolvimento dos cálculos, as implementações e seus respectivos resultados.

Introdução

O objetivo do trabalho é realizar a implementação do modelo SIR e de um modelo simplificado do proposto pelo artigo "An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics" utilizando Monte Carlo.

O modelo apresentado por Marco Amaral, et al propõe que o indivíduo escolha fazer a quarentena dependendo do risco que observa a partir da quantidade de infectados no sistema. Acoplada à escolha pela quarentena está o modelo SIR com parâmetros distintos para indivíduos não isolados e isolados. Para realizar a simulação os autores utilizam a teoria de campo médio, obtendo ondas de infecção ao longo do tempo.

Neste trabalho, a escolha do indivíduo pela quarentena se dará de acordo com o estado do seus vizinhos mais próximos - utilizado o dilema do prisioneiro -, enquanto a evolução dos infectados no sistema será realizada com o modelo SIR tal como na referência citada. Para a simulação foi utilizado o método de Monte Carlo.

O esquemático do modelo SIR com a escolha da quarentena pode ser visto na seção Modelo SIR com quarentena voluntária.

Modelos

Modelo SIR

Esquemáto modelo SIR

Em 1927 Kermack e McKendrick elaboraram o modelo SIR que tinha como função descrever o comportamento de uma pandemia . O modelo SIR é um dos mais simples modelos comportamentais, o qual descreve a variação de três parâmetros ao longo do tempo:

• Suscetível (S): Número de indivíduos suscetíveis. Quando um indivíduo suscetível e um infectado entram em contato, o indivíduo suscetível tem uma probabilidade de contrair a doença, caso contraia o indivíduo deixa de ser suscetível e torna-se infectado.

• Infectado (I): Número de indivíduos infectados. Indivíduos infectados tem uma probabilidade de infectar indivíduos suscetíveis quando em contato, e uma probabilidade de tornar-se indivíduos removidos a medida que tempo avança.

• Recuperado ou Removido (R): Número de indivíduos removidos (recuperados ou mortos pela doença). Indivíduos que foram infectados, tornam-se recuperados ou mortos pela doença, desta forma entram na classificação de indivíduos removidos, já que não são mais suscetíveis a pegar a doença, pois adquiriram imunidade. Assumindo que o número de mortos é irrelevante ao se comparar com a população total, então o parâmetro R recebe o nome de indivíduos recuperados ou resistentes.

A dinâmica de uma epidemia geralmente é mais rápida do que os números de nascimentos e óbitos, por essa razão se omite estás quantidades no modelo comportamental simples do SIR. Usando uma população fixa, Kermack e McKendrick chegaram nas seguintes equações diferencias que descrevem a dinâmica de uma epidemia :

${\frac {dS}{dt}}=-\beta IS\qquad (1)$

${\frac {dI}{dt}}=\beta IS-\gamma I\qquad (2)$

${\frac {dR}{dt}}=\gamma I\qquad (3)$

O sistema descrito pelas equações acima é não linear, porém é possível derivar uma solução analítica de forma implícita .

A população total no SIR é constante, e pode ser expressa pela soma total dos indivíduos suscetíveis, infectados e removidos. Abaixo segue a expressão:

$S+I+R=N\qquad (4)$

Na forma normalizada a expressão (4) é representada por:

$s+i+r=1\qquad (5)$

A taxa de transmissão da doença é dada pela variável beta, está depende de outras duas variáveis. A primeira indica a "transmissibilidade", definida por Tau, a segunda indica o "número médio de contatos" entre infectados e suscetíveis, indicada por "c barra". Portanto, pode-se escrever a taxa de transmissão pela expressão:

$\beta =\tau {\bar {c}}\qquad (6)$

A taxa de remoção da doença, indicada por γ, é o inverso do período infeccioso, indicada por d, que o indivíduo permanecerá doente. Note, que quanto maior o período infeccioso, mais demorada é a remoção de Infectados para Removidos.

$d={\frac {1}{\gamma }}\qquad (7)$

Dinâmica do Modelo SIR e o Número de Reprodução

O número básico de reprodução, $R_{0}$, corresponde ao número médio de pessoas que serão contagiadas pela doença quando um indivíduo infectado é introduzido em uma população completamente suscetível .

$R_{0}={\frac {\beta }{\gamma }}S_{0}\qquad (8)$

Conforme o valor de $R_{0}$ temos o seguinte comportamento :

• $R_{0}>1\Rightarrow$ epidemia crescente;
• $R_{0}=1\Rightarrow$ equilíbrio endêmico;
• $R_{0}<1\Rightarrow$ epidemia decrescente.

Podemos interpretar melhor o comportamento do número de reprodução analisando o comportamento da curva I(S), para obter essa função iremos dividir a expressão (2) pela expressão (1) e posteriormente integrar ambos os lados da igualdade, desta forma chegamos em:

$I(S)={\frac {\gamma }{\beta }}lnS-{\frac {\gamma }{\beta }}lnS_{0}-S+I_{0}+S_{0}\qquad (9)$

Derivando a expressão (9) em relação a S observa-se que a função atinge o ponto de máximo quando S = γ/β. Nas situações em que temos S < γ/β e S > γ/β, obtemos respectivamente o comportamento crescente e decrescente para função I(S). Na sequência é plotada a curva I(S) para diferentes valores de $S_{0}$. Observe que o sentido da abscissa S é negativo para o avanço da pandemia.

Figura

Quando a condição inicial $S_{0}$ está a direita da reta S = γ/β a epidemia irá aumentar o seu número de infectados, pois $R_{0}$ é maior que um. O número de infectados irá aumentar até o número de indivíduos suscetíveis ser igual a γ/β, posteriormente o número de infectados irá decair. Já quando a condição inicial $S_{0}$ está a esquerda da reta S = γ/β a epidemia irá diminuir o seu número de infectados, pois $R_{0}$ é menor do que um.

Modelo SIR com quarentena voluntária

Esquemáto modelo SIR com quarentena voluntária em suscetíveis

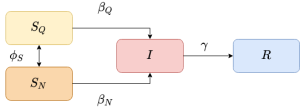
No esquemático pode-se ver o modelo utilizado no trabalho, ele é uma simplificação do artigo escrito por Amaral, et al . Nele temos:

• Componentes suscetíveis podem estar ou não em quarentena. A probabilidade $\phi _{S}$ para a escolha da quarentena ocorrer depende de quantos infectados há nos vizinhos.

• Ao escolher estar ou não em quarentena, esses componentes tem probabilidades diferentes de adquirir a doença ($\beta _{Q}$ e $\beta _{N}$) e se tornar infectados.

• Infectados possuem a mesma probabilidade de se tornarem recuperados.

• Após recuperados da doença, as pessoas não conseguem adquiri-lá novamente.

• Todos os indivíduos escolhem estar ou não isolados, modificando a escolha do vizinho, mas somente a quarentena dos suscetíveis afeta a evolução SIR.

Para simular a quarentena voluntária é utilizado o jogo definido pelo Dilema do Prisioneiro. Esse dilema descreve a situação onde dois condenados (A e B) precisam decidir se colaboram ou não sem saber a decisão do seu par. Para isso temos 4 possibilidades: A e B colaboram (ambos saem com uma recompensa R), A colabora mas B não colabora (B ficaria com o valor da tentação T e A com o custo do sonso S), o caso contrário onde A não colabora e B colabora e A e B não colaboram (ambos ganham com uma penalidade P).

Essas possibilidades podem ser resumidas em uma matriz de perdas e ganhos (matriz de payoff):

	A coopera	A não coopera
B coopera	R / R	S / T
B não coopera	T / S	P / P

Os valores da matriz payoff devem obedecer a ordem T > R > P > S. Além disso, para simulações com várias iterações deve ser obedecido que 2R > T + S.

A proposta de observar a evolução da infecção dependendo da quarentena precisa utilizar mais de um par de interagentes, por isso é definido uma rede onde cada componente possui um ponto fixo. A partir disso, cada um desses componentes interagem com seus quatro vizinhos mais próximos (para os pontos do contorno é utilizado que as bordas são unidas por condições de contorno periódicas).

Segundo Hauert e Szabó , os colaboradores tendem a ser extintos em jogos que consideram a interação aleatória, independente da sua concentração inicial, ou seja, todos tendem a não ganhar nada (não colaborar mutuamente) a fim de reduzir custos. Enquanto isso, se for proposto que um componente só escolhe uma estratégia conforme seus vizinhos, é visto é a formação de clusters de cooperadores e de não cooperadores; com isso, os componentes que estão na borda desses espaços, ganham na interação com os vizinhos colaboradores e perdem com a outra interação.

Esse jogo de quarentena é acoplado ao sistema SIR anteriormente descrito. A única diferença para o SIR sem o jogo é que as probabilidades de um componente S se tornar infectado mudam a partir do seu estado de quarentena.

Implementação

Os códigos da simulação foram implementados na linguagem C, para a visualização foi utilizada a linguagem Python. Ambos scripts estão disponíveis no projeto criado no Replit

Implementação modelo SIR com quarentena voluntária

Algumas modificações são realizadas no código anterior: a probabilidade do indivíduo passar de suscetível a infectado depende da escolha pela quarentena e é adicionada a parte da escolha individual.

Inicialmente é definida a matriz de payoff, os diferentes parâmetros de infecção para indivíduos suscetíveis e os vetores que conterão os estados de quarentena. A seguir é possível visualizar o fluoxograma para cálculo.

Resultados e Discussão

• ?

• evolução temporal monte carlo SIR com jogo

• evolução temporal monte carlo SIR com jogo e quantidade de quarentenados por passo

• evolução temporal monte carlo SIR com jogo e SIR normal

• animações com quarentenados e sir (acho que o pessoal gosta)

Os resultados obtidos mostram que a quarentena voluntária diminui significativamente o número de infectados em um primeiro momento bem como a taxa de contaminação (em relação ao SIR normal), o que era esperado uma vez que os dados da evolução da Covid-19, em países que conseguiram obter níveis de isolamento adequados, expressam um comportamento semelhante. [referencia pra essa frase].

Outro comportamento observado nos dados da Covid-19, foi o aparecimento de ondas de contaminação, isto é, uma sucessão de aumentos e diminuições na taxa de contaminação ao longo do tempo. Esse comportamento foi atribuído pelo grupo à adesão (ou não) da população à estratégia da quarentena voluntária, fator que dependeria da percepção da pandemia pela população. Assim como observados em outros artigos, esperava-se que esse comportamento fosse replicado nas simulações. Apesar disso, foi observado que tanto os parâmetros da matriz de payoff e os da dinâmica SIR quanto o sistema inicial da quarentena, interferem na evolução da doença de maneiras diferentes, esse conjunto de parâmetros ideais (supondo que existam) para obter as ondas de infecção ao longo do tempo não foram encontrados.

O não aparecimento das ondas de contaminação pode ser resultado do método utilizado, já que essa abordagem considera apenas os primeiros vizinhos no momento da escolha da estratégia, e não o total.

Abaixo são comparadas as curvas do modelo SIR com quarentena voluntária variando o estado inicial do sistema em relação ao isolamento dos indivíduos.

- % de quarentenas random - todos eles de um lado - todos eles no centro