Clusterização

PÁGINA EM CONSTRUÇÃO

Clusterização do Modelo de Ising

Balanço Detalhado

Para respeitarmos o Balanço Detalhado, precisamos que a mudança da rede de um estado $$\nu$ para um estado $\mu$ ocorra com a mesma probabilidade da mudança de um estado $\mu$ para $\nu$, denotamos essa mudança por: $A(\mu \to \nu )=A(\nu \to \mu )$, com $A(x\to y)$ sendo a razão de aceitação da mudança de um estado $x$ para um estado $y$.

Supondo que estamos mudando de um estado $\nu$ para outro estado $\mu$, temos que a diferença de energia entre esses dois é resultado da quebra das ligações entre pares de spins orientados na mesma direção que não foram adicionados ao cluster, já que, não há uma garantia que a ida de $\nu \to \mu$ quebre a mesma quantidade de ligações que a volta de $\mu \to \nu$. A probabilidade de não adicionarmos um spin vizinho ao cluster é dada por: $1-P_{add}$; uma vez que $P_{add}$ é a probabilidade de incluir esse spin no cluster.

Supondo que existam $m$ ligações a serem quebradas na ida de $\nu \to \mu$, a probabilidade desse evento é dada por $(1-P_{add})^{m}$. Porém, o mesmo pode não valer para a volta de $\mu \to \nu$, em razão disso, precisamos analisar o caso em que não há o mesmo número de ligações a serem quebradas na volta e então a probabilidade será dada por $(1-P_{add})^{n}$ com $n$ sendo o número de ligações a serem quebradas de $\mu \to \nu$.

Consideramos agora que $E_{\nu }$ e $E_{\mu }$ sejam as energias associadas aos estados $\nu$ e $\mu$, respectivamente, temos que: a cada $m$ ligações que são quebradas de $\mu \to \nu$ a energia aumenta com $+2J$ e para cada $n$ novas ligações geradas de $\mu \to \nu$ a energia diminui com $-2J$. Pode-se escrever então que a diferença de energia entre $\mu$ e $\nu$ é dada por: $E_{\nu }-E_{\mu }=2mJ-2nJ=2J(m-n)$

Seguindo a definição do Balanço Detalhado e impondo que o Processo Markoviano dessas mudanças de estados descritas acima respeite a Distribuição de Boltzmann, precisamos que: ${\frac {(1-P_{add})^{m}A(\mu \to \nu )}{(1-P_{add})^{n}A(\nu \to \mu )}}=e^{-\beta (E_{\nu }-E_{\mu })}=(1-P_{add})^{m-n}{\frac {A(\mu \to \nu )}{A(\nu \to \mu )}}$, tal que, ${\frac {A(\mu \to \nu )}{A(\nu \to \mu )}}={\big [}e^{2\beta J}(1-P_{add}){\big ]}^{n-m}\;\;\;\;\Longrightarrow P_{add}=1-e^{-2\beta J}\Longrightarrow {\frac {(1-P_{add})^{m}A(\mu \to \nu )}{(1-P_{add})^{n}A(\nu \to \mu )}}=1$

Algoritmo de Wolf

Dinâmica do Algoritmo

O algoritmo de Wolff baseia-se principalmente em 4 passos. são estes:

• 1 - Escolhe-se um sítio aleatório da rede;
• 2 - Entre seus 4 vizinhos, se o spin do vizinho for igual ao do sítio inicial, adicionamos o vizinho ao cluster com probabilidade $P_{add}=1-e^{2\beta J}$
• 3 - Para cada vizinho que foi adicionado ao cluster no passo anterior, repetimos o processo do passo 2 adicionando os vizinhos desse vizinho que possuem spin na mesma direção com a mesma probabilidade $P_{add}$. Faz-se isso para todos os sítios que são adicionados ao cluster.
• 4 - Quando todos os vizinhos de todos os sítios adicionados ao cluster tiveram ao menos uma “chance” de serem adicionados ao cluster, flipamos o cluster.

Dinâmica do algoritmo.
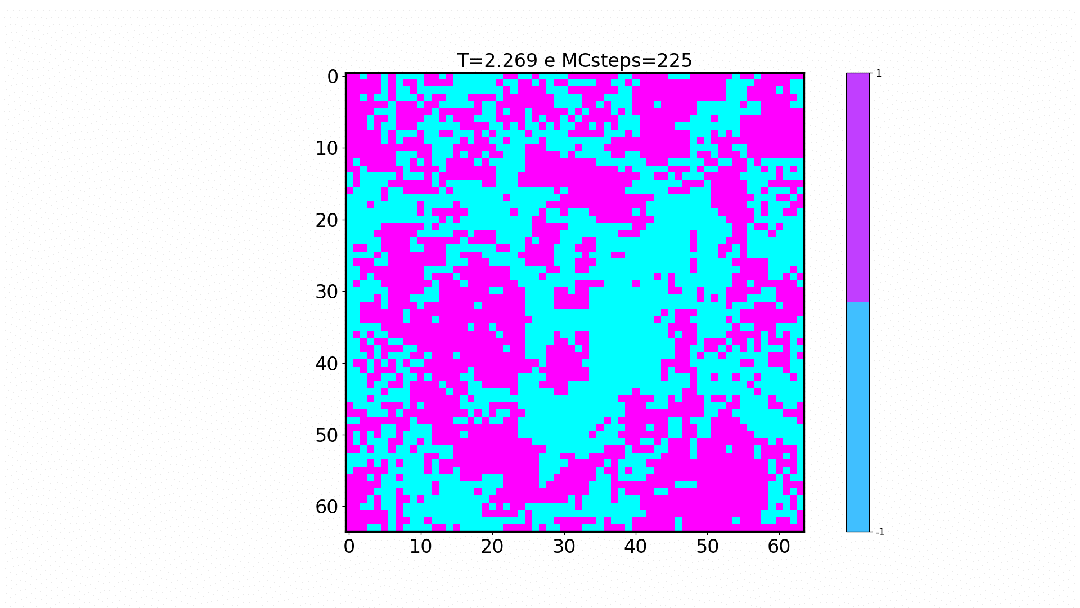Demonstração da dinâmica de clusterização do algoritmo na temperatura crítica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \; T_c = 2.269J } .

Simulações

Animações

Animações do algoritmo de Wolff em função da Temperatura Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} .
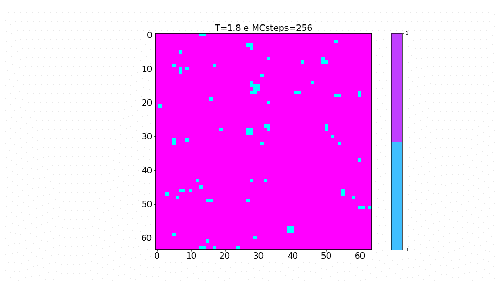Simulação para temperatura abaixo da temperatura crítica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} .	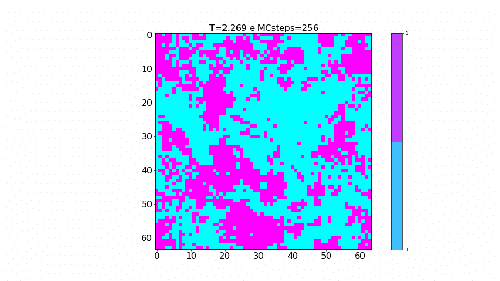Simulação na temperatura crítica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} .	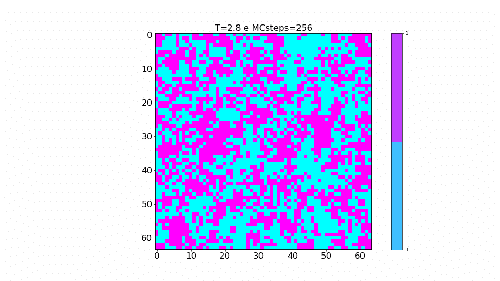Simulação para tempetura acima da temperatura crpitica Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c} .

Obs: Nossos gifs ficaram com mais de 2mb, limite da wiki, estamos refazendo...

Propriedades do Algoritmo de Wolff

Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{add}\;= \;1 - e^{-2\beta J} }

Probabilidade em função da temperatura.

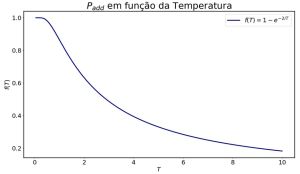Gráfico da probabilidade de aceitação Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{add}} em função de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T}