Problema de Fermi-Pasta-Ulam

Grupo: Augusto M Giani e Henrique Padovani

O objetivo deste trabalho é replicar os resultados do problema proposto por Fermi-Pasta-Ulam em 1953 sobre sistemas dinâmicos não lineares. As análises serão sobre a solução dos modos de vibração comparados à solução analítica para poucas massas e também sobre a energia do sistema para os modos de oscilação, enquanto o sistema evolui no tempo.

O Problema

O Problema proposto constitui-se de simulações em uma rede de partículas ligadas entre si através de molas que obedecem a Lei de Hooke com uma correção não-linear quadrática ou cúbica

• 

  Figura 1. Problema de Fermi-Pasta-Ulam, molas acopladas.

A lei de forças que rege o comportamento deste sistema é:

$F=-k\Delta x-\alpha k\Delta x^{2}-\beta k\Delta x^{3}$.

Onde $\Delta x$ e a deformação a cada 2 massas acopladas ($x_{i+1}-x_{i}$), $k$ é a constante elástica da mola, $\alpha$ é um parâmetro de deformação arbitrário que controla a correção não linear quadrática e $\beta$ é o parâmetro que controla a correção cúbica. Importante ressaltar que se $\alpha$ é possuir assumir um valor não nulo, real, $\beta$ é igual a zero no nosso sistema, ou vice-versa. Não estamos analisando correções quadráticas somadas com correções cúbicas neste trabalho.

Motivação: O que era esperado e o paradoxo XXX

Escrever a motivação ...

Discretização

A discretização deste problema gira em torno de abrir a equação das forças, e com o termo de aceleração, iterar o movimento das partículas a partir disso . Partimos do problema com correção quadrática, ou seja, $\beta =0$. Partindo de:

$F=-k\Delta x-\alpha k\Delta x^{2}$,

subtituímos pelas variáveis discretas:

$m{\ddot {x_{j}}}=-k\left((x_{j+1}-x_{j})-(x_{j}-x_{j-1})\right)-\alpha k\left((x_{j+1}-x_{j})-(x_{j}-x_{j-1})\right)$,

Chegamos em:

$m{\ddot {x_{j}}}=k\left(x_{j+1}-2x_{j}+x_{j-1}\right)\left[1+\alpha \left(x_{j+1}-x_{j-1}\right)\right]$

Em que ${\ddot {x_{j}}}$ é a aceleração da j-ésima partícula, com ela conseguimos integrar o movimento das partículas.

Implementação

Usamos XX partículas, com modo de oscilação YY

Resultados

SUBTITULOS

negrito, Simultaneous OverRelaxation

${\begin{cases}\Phi (x=0,y)=\Phi _{0}=1\\\Phi (x=L,y)=\Phi (x,y=0)=\Phi (x,y=L)=0\\\end{cases}}$

• 

  Problema da borda carregada eletricamente.
• 

  Gráfico da solução analítica somando até o termo n=199.

### Exemplo da evolução temporal no método de relaxação ###
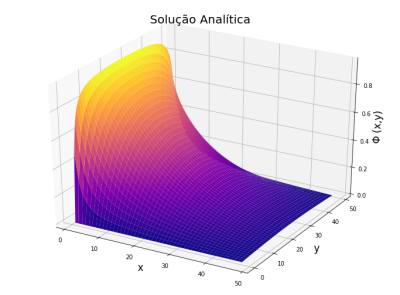
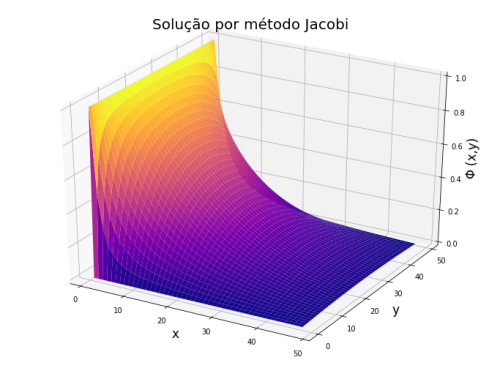
### Exemplo para o algoritmo de jacobi, Equação de Laplace ###
# P é a matriz do potencial no tempo n
# Q é a matriz do potencial no tempo n+1

while t < tmax: # Loop temporal
  
  for i in range(1,L+1):  # Loop em x
    for j in range(1,L+1): # Loop em y
      Q[i][j] = (P[i+1][j] + P[i-1][j] + P[i][j+1] + P[i][j-1])/4 
  
  P = Q.copy()
  t = t + td

plt.plot(x,y,P) # plotagem dos gráficos

Solução numérica do problema da borda carregada.

• 

  Erro relativo médio para a solução de Gauss-Seidel para várias iterações.

Link para Códigos

Fizemos no ambiente Colab em .ipynb, segue link do github:[1]