Julia

Julia é uma linguagem relativamente nova de programação que começou a ser desenvolvida em 2009 por Jeff Bezanson, Stefan Karpinski, Viral B. Shah, e Alan Edelman, um grupo do MIT. Ela foi oficialmente lançada para o mundo em 2012.

Em uma entrevista, quando perguntaram a Alan o por quê do nome Julia, ele disse que numa conversa anos atrás alguém sugeriu que Julia seria um bom nome para uma linguagem de programação.

Julia pode ser usada para propósitos gerais de programação, assim como Python, mas em sua criação foi visada a utilização de Julia para Cálculo Numérico.

Aspectos Gerais

Julia é uma linguagem de alto nível, isso significa, de maneira sucinta, que ela não é executada utilizando somente o processador, assim como acontece com linguagens de baixo nível, como Assembly, por exemplo.

É escrita em C, C++, e Scheme, usando a estrutura do compilador LLVM (para melhor entendimento, o compilador de C é o GCC, por exemplo), enquanto a maior parte da biblioteca padrão de Julia é implementada na própria Julia.

Um fato importante sobre Julia para os programadores de Python é que todas as bibliotecas de Python são usáveis através de um comando simples: PyCall.

Um fato importante sobre Julia para os programadores de C é que Julia possui APIs (Interfaces de Programação de Aplicativos) especiais para chamada de funções em C diretamente.

Velocidade

De acordo com testes feitos pelos próprios criadores de Julia, sua velocidade é similar com a de C.

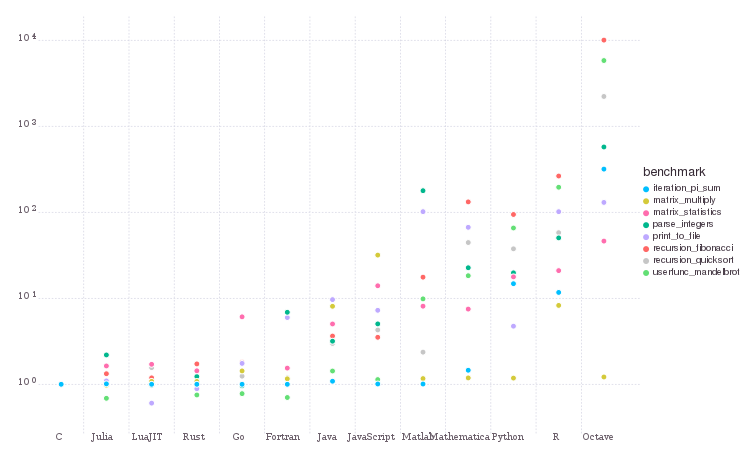
Fonte: [1]

Testes de Velocidade

A fim de pessoalmente testar a velocidade da linguagem de programação, foi escrito um programa em Julia de maneira similar ao programa de Python para o FTCS aplicado na Equação de Difusão (também conhecida como Equação do Calor).

A Equação da Difusão em uma dimensão pode ser escrita da forma:

${\frac {df}{dt}}={\frac {d^{2}f}{dx^{2}}}$

No método de FTCS (Forward-Time Central-Space) definimos a derivada em t na forma não simetrizada (forward) e as derivadas em x na forma simetrizada:

${\frac {df}{dt}}={\frac {f(x,t+dt)-f(x,t)}{dt}}$

${\frac {d^{2}f}{dx^{2}}}={\frac {f(x+dx,t)+f(x-dx,t)-2f(x,t)}{dx^{2}}}$

E substuindo na equação da difusão, em notação discreta temos:

$f_{j}^{n+1}=f_{j}^{n}+D{\frac {dt}{(dx)^{2}}}[f_{j+1}^{n}+f_{j-1}^{n}-2f_{j}^{n}]$

Observação: esse procedimento funciona bem se $k=D{\frac {dt}{(dx)^{2}}}<=1/2$, segundo análise de estabilidade do método.

Dessa forma, foi escrito um programa para integrar a Equação de Difusão através do método de FTCS nas linguagens Python e Julia.

Para Python:

//FTCS aplicado na equacao da difusao. Linguagem: PYTHON

import copy
import numpy as np
import matplotlib.pyplot as plt

def init():
	L=50;D=1.;dt=0.05;dx=1.;t=0;tmax=100.
	k=D*dt/(dx*dx)    
	return L,k,dt,t,tmax

L,k,dt,t,tmax = init()

x = np.arange(0,L,1)	
f = np.zeros(x.shape)

a = int(L/3)
b = int(2*L/3)
f[a:b]=1.
f1 = copy.deepcopy(f)	
f2 = copy.deepcopy(f)

while t<tmax:
    t+=dt
    f1[1:L-1]=f[1:L-1]+k*(f[0:L-2]+f[2:L]-2*f[1:L-1])
    f1[L-1]=f[L-1]+k*(f[L-2]+f[0]-2*f[L-1])	
    f1[0]=f[0]+k*(f[1]+f[L-1]-2*f[0])		
    f=copy.deepcopy(f1)		

sum0=sum(f1)
sum1=sum(f2)	

print("Integral em t=0: %7.4f" % sum0)
print("Integral em tmax: %7.4f" % sum1)

plt.plot(x,f,x,f2)
plt.show()

Em Julia:

//FTCS aplicado na equacao da difusao. Linguagem: JULIA

using PyPlot

L=50
D=1.
dt=0.05
dx=1.
t=0
tmax=100.
k=D*dt/(dx*dx)  

x = collect(0:1:L-1)
f = zeros(L)
f1 = zeros(L)

a = trunc(Int, L/3) 
b = trunc(Int, 2*L/3)

f[a+1:b] .= 1.
f2 = deepcopy(f)

while t<tmax
	global t+=dt	
	f1[2:L-1] = f[2:L-1] + k*(f[1:L-2] + f[3:L] - 2*f[2:L-1])		
	f1[L] = f[L] + k*(f[L-1] + f[1] - 2*f[L])
	f1[1] = f[1] + k*(f[2] + f[L] - 2*f[1])	
	global f = deepcopy(f1)		
end

sum0 = sum(f1)
sum1 = sum(f2)

println("Integral em t=0: ", sum0)
println("Integral em tmax: ", sum1)

plt.plot(x,f,x,f2)
plt.show()