Grupo - Conservação do Parâmetro de Ordem: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| Linha 4: | Linha 4: | ||
Apesar da estrutura matemática muito similar ao modelo de Ising, o modelo de CPO com sua simples condição de conservação do parâmetro de ordem aliado a condições de contorno permite que se modele sistemas marcadamente diferentes do tradicional sistema de ferromagneto tais como o gás de rede onde é possível estudar o comportamento de interfaces vapor-sólido ou vapor-líquido em condições de equilíbrio como por exemplo o equilíbrio entre água líquida e seu vapor ou entre gelo e vapor d'água. | Apesar da estrutura matemática muito similar ao modelo de Ising, o modelo de CPO com sua simples condição de conservação do parâmetro de ordem aliado a condições de contorno permite que se modele sistemas marcadamente diferentes do tradicional sistema de ferromagneto tais como o gás de rede onde é possível estudar o comportamento de interfaces vapor-sólido ou vapor-líquido em condições de equilíbrio como por exemplo o equilíbrio entre água líquida e seu vapor ou entre gelo e vapor d'água. | ||
O gás de rede é um modelo simplificado de um gás real onde se associa a cada ponto da rede uma partícula (átomo) ou sua ausência (vacância). Ao contrário do gás real a coordenada do movimento não é contínua, pois as partículas se movem de maneira discreta somente pelos vértices da rede. | O gás de rede é um modelo simplificado de um gás real onde se associa a cada ponto da rede uma partícula (átomo) ou sua ausência (vacância). Ao contrário do gás real a coordenada do movimento não é contínua, pois as partículas se movem de maneira discreta somente pelos vértices da rede. | ||
| Linha 125: | Linha 123: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>\frac{1}{2}(1-|m|) = \rho_- \le \rho \le \rho_+ = \frac{1}{2}(1+|m|)</math></div> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>\frac{1}{2}(1-|m|) = \rho_- \le \rho \le \rho_+ = \frac{1}{2}(1+|m|)</math></div> | ||
Para valores de <math>\rho</math> fora do intervalo <math>\rho_- \le \rho \le \rho_+</math> ainda é possível que uma região do sistema favoreça uma das duas densidades preferenciais. Suponha que se tenha <math>\rho < \rho_-</math>. Nesse caso o sistema possui menos partículas do que precisa pra atingir o a densidade <math>\rho_+</math>. Ainda que localmente seja possível o sistema atingir a densidade <math>\rho_+</math> isso leva a uma falta ainda maior de partículas em outras regiões do sistema sendo, portanto, energeticamente custoso. A opção energeticamente mais favorável adotada pelo sistema é distribuir as poucas partículas homegeneamente pela rede. Esse comportamento é observado na simulação. | Para valores de <math>\rho</math> fora do intervalo <math>\rho_- \le \rho \le \rho_+</math> ainda é possível que uma região do sistema favoreça uma das duas densidades preferenciais. Suponha que se tenha <math>\rho < \rho_-</math>. Nesse caso o sistema possui menos partículas do que precisa pra atingir o a densidade <math>\rho_+</math>. Ainda que localmente seja possível o sistema atingir a densidade <math>\rho_+</math> isso leva a uma falta ainda maior de partículas em outras regiões do sistema sendo, portanto, energeticamente custoso. A opção energeticamente mais favorável adotada pelo sistema é distribuir as poucas partículas homegeneamente pela rede. Esse comportamento é observado na simulação. | ||
| Linha 134: | Linha 130: | ||
* E outra em que <math>\rho\not\in[\rho_-,\rho_+]</math> tendo densidade homogênea | * E outra em que <math>\rho\not\in[\rho_-,\rho_+]</math> tendo densidade homogênea | ||
Com <math> | Com <math>\rho</math> sujeito ao intervalo <math>\frac{1}{2}(1-|m|) \le \rho \le \frac{1}{2}(1+|m|)</math> conclui-se que <math>/rho</math> pode assumir um intervalo menor de valores a medida que <math>|m|</math> diminui. A magnetização diminui sob o aumento da temperatura. Acima da temperatura crítica a <math>|m|=0</math> e portanto o intervalo <math>\frac{1}{2}(1-|m|) \le \rho \le \frac{1}{2}(1+|m|)</math> reduz-se a zero evidenciando que não existe mais um valor de <math>\rho</math> que evite a homogeinização da rede. | ||
A discussão acima pode ser apresentada resumidamente pelo diagrama de fases: | A discussão acima pode ser apresentada resumidamente pelo diagrama de fases: | ||
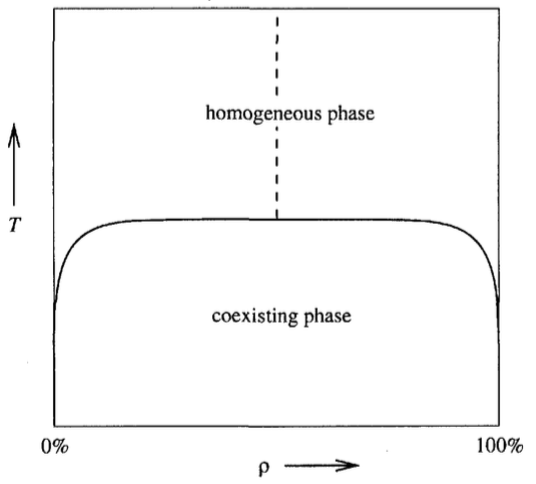
[[Arquivo:Cop_phase_diagram.png|frame| | [[Arquivo:Cop_phase_diagram.png|frame|50px|center|Diagrama de fases do modelo CPO. Fase homogênea para temperaturas além da temperatura crítica e fase coexistente abaixo com densidades preferenciais <math>\rho_+</math> e <math>\rho_-</math>]] | ||
Esse comportamento é observado quando se diminui a temperatura de vapor d'agua que passa a formar gotas líquidas que coexistem com o vapor para um intervalo de temperaturas. A fase condensada do gás de rede, no entanto, é mais adequadamente interpretada como um sólido devido a posição fixa das partículas (análogas a moléculas ou átomos) na rede, dessa forma, falamos de interface vapor/sólido ao invés de vapor/líquido. | Esse comportamento é observado quando se diminui a temperatura de vapor d'agua que passa a formar gotas líquidas que coexistem com o vapor para um intervalo de temperaturas. A fase condensada do gás de rede, no entanto, é mais adequadamente interpretada como um sólido devido a posição fixa das partículas (análogas a moléculas ou átomos) na rede, dessa forma, falamos de interface vapor/sólido ao invés de vapor/líquido. | ||
| Linha 144: | Linha 140: | ||
==Implementação== | ==Implementação== | ||
Sistemas físicos em equilíbrio com muitos graus de liberdade e no limite termodinâmico comportam-se de tal forma que ao flutuarem de um estado <math>\mu</math> para um estado <math>\nu</math> tem-se que <math>\nu</math> difere pouco de <math>\mu</math>. Outra maneira de dizer isso é que as flutuações dessa tipo de sistema físico são muito pequenas em relação ao número de configurações possíveis e que portanto o sistema passa a maior parte do tempo alternando entre um pequeno conjunto de configurações. A consequência disso é que pode-se escolher uma estratégia de visitar com maior probabilidade apenas a fração de estados do sistema, as quais mais contribuem para atingir o equilíbrio ao invés de se visitar todos os estados indistintamente. No modelo de ferromagneto, por exemplo, com uma rede <math>10\times 10\times 10</math>, há <math>2^{1000} \simeq 10^{300}</math> configurações possíveis sendo que mesmo com um supercomputador seria impraticável realizar essa simulação. O método de Monte Carlo consiste em visitar eficientemente uma pequena fração desses estados e atingir rapidamente o equilíbrio em poucos passos e o peso que define como visitar o estado seguinte é dado pela distribuição de Boltzmann <math>e^{\beta(E_\nu-E_\mu)}</math> onde fica claro que quanto mais diferente <math>\nu</math> for de <math>\mu</math> menor a change de fazer a transição <math>\mu\to\mu</math> | |||
Dessa forma impõe-se que no equilíbrio o sistema obedeça a distribuição de Boltzmann, portanto a condição de balanço detalhado dá liberdade na escolha de <math>P(\mu\to\nu)</math> e <math>P(\nu\to\mu)</math> desde que seja satisfeita: | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>\frac{g(\mu)}{g(\nu)}\frac{A(\mu\to\nu)}{A(\nu\to\mu)} = e^{\beta(E_\nu-E_\mu)}</math></div> | |||
Uma possível escolha para <math>A(\mu\to\nu)</math> seria: | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>A(\mu\to\nu)=A_0e^{-\frac{1}{2}\beta(E_\nu-E_\mu)}</math></div> | |||
Como <math>A_0</math> é cancelada na razão entre probabilidades de aceitação temos a liberdade na sua escolha desde que mantenha a probabilidade menor ou igual a um. No modelo de Ising, por exemplo, a maior diferença de energia que se pode obter entre estados é <math>\Delta E = E_\nu-E_\mu = \pm 2zJ</math> o que significa que o maior valor de <math>e^{-\frac{1}{2}\beta(E_\nu-E_\mu)}</math> é justamente <math>e^{\beta zJ}</math>. Assim, para garantir que a probabilidade seja menor ou igual a 1 deve-se escolher <math>A_0 \le e^{-\beta zJ}</math> | |||
Para que o algoritmo seja eficiente deseja-se que a probabilidade de aceitação seja a maior possível, pois do contrário estaríamos utilizando tempo computacional apenas para rejeitar trocas de estado. Portanto queremos que <math>A_0</math> assuma o maior valor possível <math>A_0 = e^{\beta zJ}</math>, maximizando <math>A(\mu\to\nu)</math>: | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>A(\mu\to\nu)=e^{-\frac{1}{2}\beta(E_\nu-E_\mu+2\beta z J)}</math></div> | |||
Devido a condição de balanço detalhado, essa escolha implica: | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>A(\nu\to\mu)=e^{-\beta z J}</math></div> | |||
Metropolis percebeu que desde que a condição de balanço detalhado seja satisfeita tem-se liberdade na escolha das probabilidades de aceitação. Então ele decidiu atribuir o maior valor possível para a probabilidade de aceitação que tem o maior valor entre as duas, no caso <math>A(\nu\to\mu)</math>, ou seja: | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>A(\nu\to\mu)=1</math></div> | |||
O que implica: | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>A(\mu\to\nu)=e^{-\beta(E_\nu-E_\mu)}</math></div> | |||
Dessa forma a transição de estados sempre ocorre se <math>E_\nu < E_\mu</math> ou seja <math>\Delta E <= 0</math> mas pode ou não ocorrer caso seja <math>\Delta E > 0</math> com uma probabilidade dada por <math>e^{-\beta(E_\nu-E_\mu)}</math>. Em suma: | |||
<math> | |||
A(\mu\to\nu) = \begin{cases} | |||
e^{-\beta(E_\nu-E_\mu)} \ \mbox{ se } \ E_\nu - E_\mu > 0\\ | |||
1 \ \mbox{ caso contrario}\\ | |||
\end{cases} | |||
</math> | |||
===Gás de rede=== | |||
Para obedecer a condição de conservação da magnetização não é permitido alterar um spin individualmente (ou um número ímpar de spins). Uma maneira de tratar a dinâmica desse sistema foi proposta por Kawasaki e consiste em simplesmente alternar o estado de spin de um par de | |||
partículas que tenham estados de spin oposto, ou seja: | |||
<math> | |||
\begin{cases} | |||
\uparrow \uparrow ou \downarrow \downarrow \quad\to\quad \text{nada a fazer} \\ | |||
\uparrow \downarrow \quad\to\quad \downarrow \uparrow\\ | |||
\downarrow \uparrow \quad\to\quad \uparrow \downarrow\\ | |||
\end{cases} | |||
</math> | |||
É evidente que nesse caso a mudança na magnetização é conservada pois a troca de spins resulta em variação de magnetização nula. | |||
Cada ponto da rede possui <math>z</math> vizinhos e portanto a cada passo de iteração deve-se sortear com qual dos vizinhos será feita uma tentativa de troca de spins. Essa escolha é feita aleatoriamente (uniforme). Uma vez escolhido um vizinho deve-se decidir se a troca deve ser feita ou não. Essa decisão é tomada com base no método de Monte Carlo, em particular, com a probabilidade de aceitação de Metropolis exatamente como exposto na seção acima. | |||
A '''ergodicidade''' é satisfeita pelo sistema pois um passo de Monte Carlo corresponde a uma troca entre vizinhos que numa rede finita pode ser efetuada a partir de outro estado qualquer em número finito de passos | |||
Como já foi mencionado a rede possui <math>N</math> pontos e número de coordenação <math>z</math> o que resulta em <math>\frac{1}{2}zN</math> pares de primeiros vizinhos, portanto, a probabilidade de selecionar um par qualquer é dada por: | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>g(\mu\to\nu) = \frac{1}{\frac{1}{2}zN} = \frac{2}{zN}</math></div> | |||
A probabilidade de seleção <math>g(\nu\to\mu)</math> é a mesma fazendo com que esses termos se cortem na condição de balanço detalhado e permitindo que se aplique a escolha de Metropolis discutida acima sem alterações. | |||
Para efetivamente tomar a decisão sobre a troca entre vizinhos onde <math>\Delta E</math> é necessário especificar como é feito seu cálculo. <math>\Delta E</math> é dado pela seguinte expressão: | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>\Delta E = E_\nu-E_\mu = 2J\left[s_k^\mu\sum_{i\not\in\{k',k\}}s_i^\mu+s_{k'}^\mu\sum_{j\not\in\{k,k'\}}s_j^\mu\right]</math></div> | |||
Seja um ponto da rede <math>k</math> e <math>k'</math> primeiro vizinho de <math>k</math>. Deseja-se calcular a energia de interação entre esse par. A expressão acima apenas diz que deve-somar os produtos do spin de <math>k</math>, <math>(s_k)</math>, com seus primeiros vizinhos <math>s_i</math> excluindo-se da soma tanto <math>k</math> quanto <math>k'</math>. Faz-se o mesmo procedimento para <math>k'</math>, ou seja, soma-se os produtos do spin <math>k'</math>, <math>(s_{k'})</math>, com todos os seus primeiros vizinhos <math>s_j</math> exceto ele mesmo e <math>k</math>. A soma dessas duas quantidades multiplicadas por <math>2J</math> é igual a diferença de energia entre a configuração <math>\mu</math> e a <math>\nu</math> | |||
==Simulação== | |||
Foram simulados três sistemas diferentes os quais são discutidos a seguir. | |||
===Interface linear=== | |||
Esse sistema como condição inicial uma rede com a região da metade inferior completamente populada por partículas | |||
[[Arquivo:cop500iterinstepsof10.gif|frame|center|description]] | |||
===Interface circular=== | |||
[[Arquivo:copSquare500iterinstepsof10.gif|frame|center|description]] | |||
[[Arquivo:copSquare100-iloveimg-compressed.gif|frame|center|description]] | |||
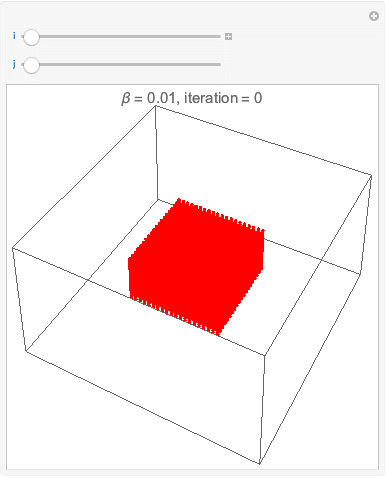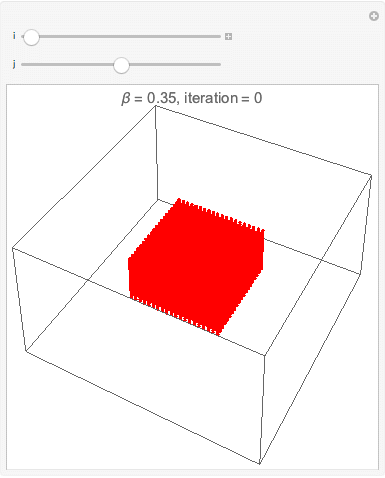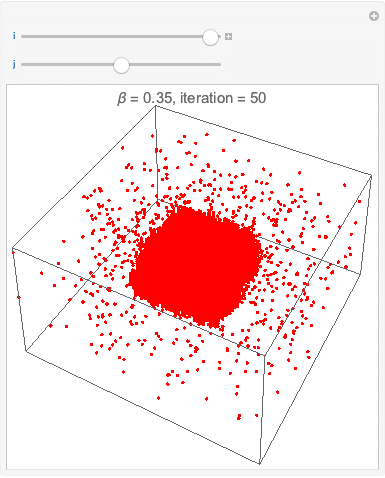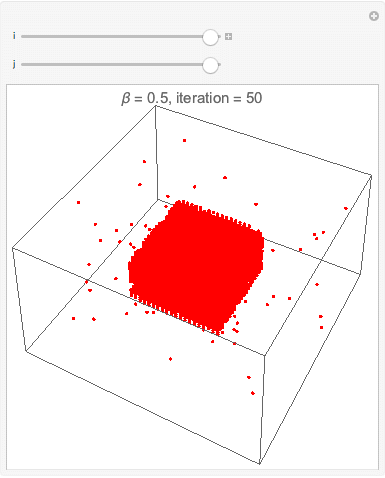
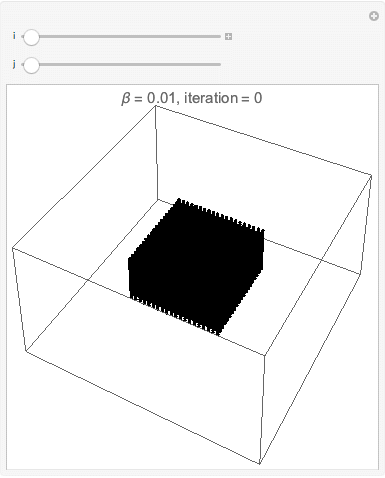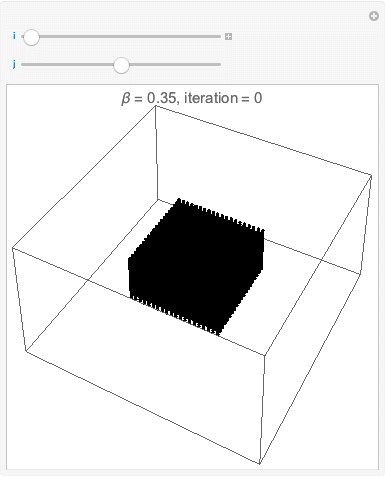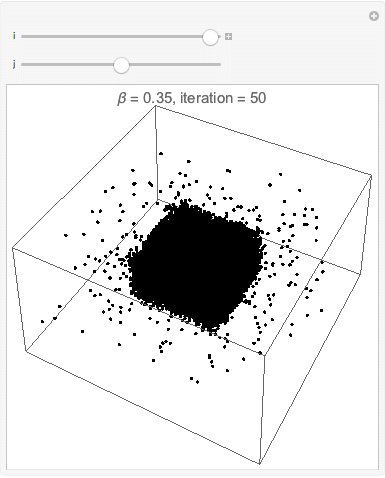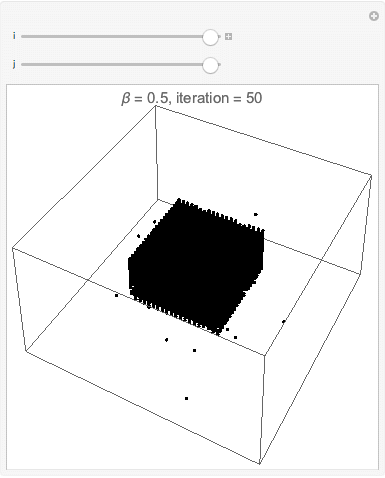
===Interface esférica=== | |||
[[Arquivo:cop3D500instepsof10.gif|frame|center|description]] | |||
[[Arquivo:cop3D250instepsof5.gif|frame|center|description]] | |||
[[Arquivo:cop3D250instepsof5round.gif|frame|center|description]] | |||
==Equilíbrio== | ==Equilíbrio== | ||
Edição das 19h19min de 24 de janeiro de 2018
Introdução
O modelo de Ising possui características universais que permitem aplicá-lo a situações diversas sendo tão versátil a ponto de descrever desde ferromagnetos até interações sociais. Dentro dessa gama de possibilidades existe o modelo de Conservação do Parâmetro de Ordem (CPO) em que, como o nome indica, mantém-se o parâmetro de ordem constante. No caso de um ferromagneto o parâmetro de ordem é a magnetização, portanto, um modelo de Ising sujeito CPO a grandeza análoga à magnetização se manteria constante a cada passo da simulação.
Apesar da estrutura matemática muito similar ao modelo de Ising, o modelo de CPO com sua simples condição de conservação do parâmetro de ordem aliado a condições de contorno permite que se modele sistemas marcadamente diferentes do tradicional sistema de ferromagneto tais como o gás de rede onde é possível estudar o comportamento de interfaces vapor-sólido ou vapor-líquido em condições de equilíbrio como por exemplo o equilíbrio entre água líquida e seu vapor ou entre gelo e vapor d'água.
O gás de rede é um modelo simplificado de um gás real onde se associa a cada ponto da rede uma partícula (átomo) ou sua ausência (vacância). Ao contrário do gás real a coordenada do movimento não é contínua, pois as partículas se movem de maneira discreta somente pelos vértices da rede. Pode-se refinar o modelo de diversas formas:
- Conferindo inércia às partículas
- Alterando a forma da rede (quadrada, hexagonal, fcc, bcc, cúbica)
- Incluindo partículas de tipos diferentes com interações comum a seu respectivo tipo
- Presença e/ou tipos de colisões
No entanto, uma versão simplificada (e simples de simular) desse modelo é suficiente para reproduzir qualitativamente o comportamento de interfaces.
Teoria
No modelo simplificado do gás de rede as partículas (sem inércia), movem-se de forma aleatória sob excitação térmica e satisfazem as seguintes condições:
- O número total de partículas é fixo: nenhuma partícula deixa ou entra no sistema, portanto, caso desapareça a partícula deve reaparecer em outro ponto da rede no mesmo passo de simulação.
- Um ponto da rede pode ser ocupado por uma única partícula ou permanecer vazio (não ocupado). Essa é uma maneira grosseira de assimilar o caráter físico de repulsão do gás real onde partículas não podem interpenetrar-se devido a exclusão de Pauli.
- Se duas partículas são primeiras vizinhas uma da outra elas sentem uma atração que é a mesma para qualquer par de partículas. Essa condição modela o efeito de atração entre partículas de um gás real.
As forças de atração e repulsão num gás real não possuem alcance de mesma ordem. A repulsão é de curto alcance enquanto a atração é de longo-alcance. Embora o presente modelo trate as partículas como se o alcance de repulsão e atração fossem da mesma ordem, ainda é possível extrair propriedades físicas que tem paralelo com o gás real tais como transições de fase e formato de interfaces.
A cada ponto da rede associamos o valor se houver uma partícula nesse ponto ou caso contrário. Representamos essa variável por , ou seja, no iésimo ponto da rede a variável pode assumir apenas os valores ou , ou resumidamente:
A conservação do número de partículas exige que se tenha:
Onde é a densidade de partículas e é o número total de partículas, sendo, portanto, o número de pontos ocupados da rede.
O hamiltoniano do sistema é modelado a partir da condição 2 exposta acima em que é especificado que um par de primeiros vizinhos na rede contribui para a diminuição da energia do sistema por uma quantidade :
Onde denota soma sobre todos os pares de primeiros vizinhos da rede.
Equivalência ao modelo de Ising
Para mostrar a equivalência com o modelo de Ising definimos a seguinte variável:
Essa nova variável é nada mais do que o spin no modelo de Ising para um ferromagneto assumindo os valores:
- quando , ou seja, posição ocupada por partícula; ou
- quando , ou seja, posição não ocupada
Em termos da variável de spin é dada por:
Substituindo no Hamiltoniano tem-se:
Seja o número de coordenação da rede, ou seja, o número de primeiros vizinhos ( para rede quadrada e para rede cúbica simples). Para uma dada rede existem possíveis pares distintos
Pode-se simplificar esssa expressão com base nas seguintes observações:
- Os somatórios em e são idênticos exceto pelo índice.
- A soma sobre pares de vizinhos é equivalente a somar vezes sobre o número de pontos da rede:
- pode ser escrito em termos das constantes e assim como ocorre com
Dessa forma o Hamiltoniano se reduz a:
Seja J = e observando que é uma constante pois todos seus termos são constantes, chegamos na equivalência com o Hamiltoniano do modelo de Ising na ausência de campo magnético:
O valor esperado de qualquer quantidade física não é alterado pela adição de uma constante ao hamiltoniano:
Conservação do parâmetro de ordem
A magnetização do sistema é nada mais do que a soma de spins que já calculamos acima:
No entanto, e devem permanecer constantes durante toda a simução, isso implica que a magnetização também é sempre constante, ou seja, a magneticação é o parâmetro de ordem conservado nesse sistema fato que dá nome ao método.
É vantajoso tratar o modelo de gás de rede sob a perspectiva de um modelo de Ising pois todo o arcabouço de técnicas amplamente conhecidas e extensivamente estudadas para o modelo de Ising podem ser aplicadas.
Apesar das similaridades, o gás de rede, como definido, possui muito menos estados válidos pois não é permitido alterar a magnetização do sistema enquanto no modelo de Ising qualquer spin individual pode ser invertido sem restrições pois a magnetização não precisa se manter constante.
Transição de fase
Aproveitando a equivalência estabelecida entre gás de rede e o modelo de Ising sabe-se que o sistema possui uma transição de fase que ocorre a uma temperatura crítica . Rearranjando a densidade de pontos (equivalente agora a spins up) tem-se:
No modelo de Ising sabe-se também que abaixo da temperatura crítica existem dois valores de equilíbrio para a magnetização que são e , portanto, para favorecer a coexistência de fases tem-se que:
Para valores de fora do intervalo ainda é possível que uma região do sistema favoreça uma das duas densidades preferenciais. Suponha que se tenha . Nesse caso o sistema possui menos partículas do que precisa pra atingir o a densidade . Ainda que localmente seja possível o sistema atingir a densidade isso leva a uma falta ainda maior de partículas em outras regiões do sistema sendo, portanto, energeticamente custoso. A opção energeticamente mais favorável adotada pelo sistema é distribuir as poucas partículas homegeneamente pela rede. Esse comportamento é observado na simulação.
Dessa forma, no caso de o sistema possui duas fases:
- Uma em que se dividindo em dois domínios cada qual favorecendo uma das duas densidades
- E outra em que tendo densidade homogênea
Com sujeito ao intervalo conclui-se que pode assumir um intervalo menor de valores a medida que diminui. A magnetização diminui sob o aumento da temperatura. Acima da temperatura crítica a e portanto o intervalo reduz-se a zero evidenciando que não existe mais um valor de que evite a homogeinização da rede.
A discussão acima pode ser apresentada resumidamente pelo diagrama de fases:
Esse comportamento é observado quando se diminui a temperatura de vapor d'agua que passa a formar gotas líquidas que coexistem com o vapor para um intervalo de temperaturas. A fase condensada do gás de rede, no entanto, é mais adequadamente interpretada como um sólido devido a posição fixa das partículas (análogas a moléculas ou átomos) na rede, dessa forma, falamos de interface vapor/sólido ao invés de vapor/líquido.
Implementação
Sistemas físicos em equilíbrio com muitos graus de liberdade e no limite termodinâmico comportam-se de tal forma que ao flutuarem de um estado para um estado tem-se que difere pouco de . Outra maneira de dizer isso é que as flutuações dessa tipo de sistema físico são muito pequenas em relação ao número de configurações possíveis e que portanto o sistema passa a maior parte do tempo alternando entre um pequeno conjunto de configurações. A consequência disso é que pode-se escolher uma estratégia de visitar com maior probabilidade apenas a fração de estados do sistema, as quais mais contribuem para atingir o equilíbrio ao invés de se visitar todos os estados indistintamente. No modelo de ferromagneto, por exemplo, com uma rede , há configurações possíveis sendo que mesmo com um supercomputador seria impraticável realizar essa simulação. O método de Monte Carlo consiste em visitar eficientemente uma pequena fração desses estados e atingir rapidamente o equilíbrio em poucos passos e o peso que define como visitar o estado seguinte é dado pela distribuição de Boltzmann onde fica claro que quanto mais diferente for de menor a change de fazer a transição
Dessa forma impõe-se que no equilíbrio o sistema obedeça a distribuição de Boltzmann, portanto a condição de balanço detalhado dá liberdade na escolha de e desde que seja satisfeita:
Uma possível escolha para seria:
Como é cancelada na razão entre probabilidades de aceitação temos a liberdade na sua escolha desde que mantenha a probabilidade menor ou igual a um. No modelo de Ising, por exemplo, a maior diferença de energia que se pode obter entre estados é o que significa que o maior valor de é justamente . Assim, para garantir que a probabilidade seja menor ou igual a 1 deve-se escolher
Para que o algoritmo seja eficiente deseja-se que a probabilidade de aceitação seja a maior possível, pois do contrário estaríamos utilizando tempo computacional apenas para rejeitar trocas de estado. Portanto queremos que assuma o maior valor possível , maximizando :
Devido a condição de balanço detalhado, essa escolha implica:
Metropolis percebeu que desde que a condição de balanço detalhado seja satisfeita tem-se liberdade na escolha das probabilidades de aceitação. Então ele decidiu atribuir o maior valor possível para a probabilidade de aceitação que tem o maior valor entre as duas, no caso , ou seja:
O que implica:
Dessa forma a transição de estados sempre ocorre se ou seja mas pode ou não ocorrer caso seja com uma probabilidade dada por . Em suma:
Gás de rede
Para obedecer a condição de conservação da magnetização não é permitido alterar um spin individualmente (ou um número ímpar de spins). Uma maneira de tratar a dinâmica desse sistema foi proposta por Kawasaki e consiste em simplesmente alternar o estado de spin de um par de partículas que tenham estados de spin oposto, ou seja:
É evidente que nesse caso a mudança na magnetização é conservada pois a troca de spins resulta em variação de magnetização nula.
Cada ponto da rede possui vizinhos e portanto a cada passo de iteração deve-se sortear com qual dos vizinhos será feita uma tentativa de troca de spins. Essa escolha é feita aleatoriamente (uniforme). Uma vez escolhido um vizinho deve-se decidir se a troca deve ser feita ou não. Essa decisão é tomada com base no método de Monte Carlo, em particular, com a probabilidade de aceitação de Metropolis exatamente como exposto na seção acima.
A ergodicidade é satisfeita pelo sistema pois um passo de Monte Carlo corresponde a uma troca entre vizinhos que numa rede finita pode ser efetuada a partir de outro estado qualquer em número finito de passos
Como já foi mencionado a rede possui pontos e número de coordenação o que resulta em pares de primeiros vizinhos, portanto, a probabilidade de selecionar um par qualquer é dada por:
A probabilidade de seleção é a mesma fazendo com que esses termos se cortem na condição de balanço detalhado e permitindo que se aplique a escolha de Metropolis discutida acima sem alterações.
Para efetivamente tomar a decisão sobre a troca entre vizinhos onde é necessário especificar como é feito seu cálculo. é dado pela seguinte expressão:
Seja um ponto da rede e primeiro vizinho de . Deseja-se calcular a energia de interação entre esse par. A expressão acima apenas diz que deve-somar os produtos do spin de , , com seus primeiros vizinhos excluindo-se da soma tanto quanto . Faz-se o mesmo procedimento para , ou seja, soma-se os produtos do spin , , com todos os seus primeiros vizinhos exceto ele mesmo e . A soma dessas duas quantidades multiplicadas por é igual a diferença de energia entre a configuração e a
Simulação
Foram simulados três sistemas diferentes os quais são discutidos a seguir.
Interface linear
Esse sistema como condição inicial uma rede com a região da metade inferior completamente populada por partículas




















































![{\displaystyle \rho \in [\rho _{-},\rho _{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc499e595fcf8c8a7ff5bb02b94a9231e387d12d)

![{\displaystyle \rho \not \in [\rho _{-},\rho _{+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c5527be819a2d89bab9d4105ca6dbf947319821)





































![{\displaystyle \Delta E=E_{\nu }-E_{\mu }=2J\left[s_{k}^{\mu }\sum _{i\not \in \{k',k\}}s_{i}^{\mu }+s_{k'}^{\mu }\sum _{j\not \in \{k,k'\}}s_{j}^{\mu }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa23051c87414cc6c8c16aaa2fd2255a1d1c79a9)