Grupo - Lennard Jones: mudanças entre as edições
| Linha 46: | Linha 46: | ||
Um problema da amostragem simples é que ela utiliza uma distribuição uniforme, que pode, pra uma função que decaia rapidamente a zero, demorar muito a estimar corretamente o valor médio da função. Porém, podemos utilizar uma distribuição <math> w(x) </math> que tenha um formato semelhante à função que queremos integrar, reescrevendo a integral | Um problema da amostragem simples é que ela utiliza uma distribuição uniforme, que pode, pra uma função que decaia rapidamente a zero, demorar muito a estimar corretamente o valor médio da função. Porém, podemos utilizar uma distribuição <math> w(x) </math> que tenha um formato semelhante à função que queremos integrar, reescrevendo a integral | ||
<math> F = \int_a^b{\frac{f(x)}{w(x)} w(x) dx} </math> | <math> F = \int_a^b{\frac{f(x)}{w(x)} w(x) dx} </math> | ||
Usando isso, faz-se a mesma integral por um processo um pouco diferente; a média, agora, será dos valores da função razão <math> \frac{f(x)}{w(x)} </math> com distribuição <math> w(x) </math> para sorteio dos pontos. Esse método faz com que seja muito mais rápida a convergência do estimador da média da função, usada para o cálculo da integral. | |||
=== Algoritmo de Metropolis === | === Algoritmo de Metropolis === | ||
Edição das 11h13min de 15 de janeiro de 2018
O potencial devido a interação entre duas partículas separadas por uma distância Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r'} pode ser modelado pelo potencial de Lennard Jones:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U'(r') = 4 \epsilon \left [ \left ( \frac{\sigma}{r'} \right )^{12} + \left ( \frac{\sigma}{r'} \right )^{6} \right ]}
Posto em unidades reduzidas (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r \equiv r'/ \sigma} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U \equiv U' / \epsilon} ), o potencial reduz-se a:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(r) = 4 \left [ \left ( \frac{1}{r} \right )^{12} + \left ( \frac{1}{r} \right )^{6} \right ]}
Trabalha-se, por conveniência, com o seguintes sistema de unidades básicas:
| Grandeza | Comprimento | Tempo | Massa | Temperatura | Energia | Pressão | Densidade |
|---|---|---|---|---|---|---|---|
| Unidade | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma \sqrt{m_p / \epsilon}} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_p} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon/k_B} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon / \sigma^3} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 / \sigma^{3}} |
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_p} é a massa da partícula e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B} é a constante de Boltzmann.
Método Monte Carlo
Denomina-se método de Monte Carlo métodos estatísticos que se baseiam em amostragem aleatória massiva para cálculo numérico.
Amostragem simples
Pode-se querer calcular uma integral numericamente utilizando Monte Carlo. Uma forma de fazer isso parte de que uma integral pode ser reescrita como
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = \int_a^b{f(x) dx} = (b - a)\langle f(x) \rangle }
Dessa forma, utiliza-se amostragem aleatória massiva para estimar Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle f(x) \rangle } , que é a média da função no intervalo de interesse.
Amostragem por importância
Um problema da amostragem simples é que ela utiliza uma distribuição uniforme, que pode, pra uma função que decaia rapidamente a zero, demorar muito a estimar corretamente o valor médio da função. Porém, podemos utilizar uma distribuição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w(x) } que tenha um formato semelhante à função que queremos integrar, reescrevendo a integral
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = \int_a^b{\frac{f(x)}{w(x)} w(x) dx} }
Usando isso, faz-se a mesma integral por um processo um pouco diferente; a média, agora, será dos valores da função razão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{f(x)}{w(x)} }
com distribuição Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle w(x) }
para sorteio dos pontos. Esse método faz com que seja muito mais rápida a convergência do estimador da média da função, usada para o cálculo da integral.
Algoritmo de Metropolis
Dado uma amostra com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} partículas, a abordagem introduzida por Metropolis segue o seguinte esquema:
(1) Selecionar uma partícula aleatóriamente, e calcular sua energia Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(r)}
;
(2) Dado o deslocamento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r_n} = \mathbf{r} + \mathbf{\Delta}}
, calcular Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(r_n)}
;
(3) Aceitar o movimento Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r} \rightarrow \mathbf{r_n}}
com probabilidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p = min\{1; \exp[-\beta (U(r_n) - U(r))]\}}
Estimadores no Equilíbrio
Em todos os exemplos tratados aqui, será usado o ensemble NVT (com o número de partículas, volume e temperatura constantes). Dado isso, os sistemas são caracterizados com um densidade e uma temperatura. Com tais sistema no equilíbrio, são estimadas (média de sucessivas medidas) a energia total e a pressão, dadas respectivamente por
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_T = \sum_i \sum_{j>i}U(r_{ij}) }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \frac{\rho}{\beta} + \frac{2}{3V}\sum_i \sum_{j>i}\mathbf{f(\mathbf{r_{ij}})} \cdot \mathbf{r_{ij}} }
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r_{ij}} = \mathbf{r_{j}} - \mathbf{r_{i}}} . Além disso, é interessante a análise da capacidade térmica
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_v = \frac{\langle U_T^2 \rangle - \langle U_T \rangle ^2}{k_BT^2}}
Detalhes Técnicos
Condições de Contorno
Qualquer sistema possível de ser feito hoje com método Monte Carlo, apesar do grande poder computacional disponível, fica distante do limite termodinâmico. As condições de contorno podem ser estabelecidas de forma a tentar driblar isso. As condições utilizadas neste trabalho foram condições de contorno periódicas, que permitem uma simulação de preenchimento, e funciona bem para sistemas isotrópicos.
Truncamento nas interações
Um problema da condição de contorno periódica é que, a princípio, cada partícula interagiria com todas as outras do sistema, que devido ao fato de ser periodicamente repetido, seriam infinitas. Como o potencial utilizado é de curto alcance, deve ser possível, de alguma forma, limitar as interações entre as partículas sem perda dos significados numéricos da simulação. Pode-se, truncar as interações de uma partícula Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } a partir de uma distância Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_c } de forma que há uma descontinuidade no potencial dessa partícula no círculo de raio Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_c } . Assim o potencial simulado é:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{trunc}(r) = \begin{cases}U_{LJ}(r) & , r \leq r_c\\0 & , r > r_c \end{cases} }
Esse é o chamado truncamento simples. O subíndice LJ se refere ao potencial de Lennard Jones. O problema é que isso cria uma contribuição indesejada à pressão, já que há uma força de impulso por conta dessa descontinuidade do potencial.
Pode-se, então, usar o truncamento com deslocamento, que evita essa descontinuidade fazendo uma subtração em todo ponto do módulo do potencial de Lennard Jones à distância Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_c } . Assim, o potencial simulado é:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{deslocado}(r) = \begin{cases}U_{LJ}(r) - U_{LJ}(r_c) & , r \leq r_c\\0 & , r > r_c \end{cases} }
Com esse potencial, que é contínuo, as forças serão sempre finitas, o que retira a força de impulso que alteraria medidas de pressão.
Translação
A possível nova posição de uma partícula será Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_n, y_n, z_n)} tal que
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_n = x + \Delta (r - 0.5)}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_n = y + \Delta (r - 0.5)}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_n = z + \Delta (r - 0.5)}
sendo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} números randômicos uniformemente distribuídos e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta } o deslocamento máximo permitido. Se a nova posição for aceita seguindo o algorítmo de Metrópolis, a partícula assumirá essa posição.
Diagramas de fase
Dado um sistema com densidade Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho } e temperatura Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} , os diagramas foram feitos com:
(A) Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = 500 }
partículas
(B) Cubo de lado Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L = (N / \rho)^{1/3} }
com condições de contorno periódicas
(C) Incialização aleatória
(D) Distância de corte Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_c = L/2 }
(E) Deslocamento máximo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta = L/2 }
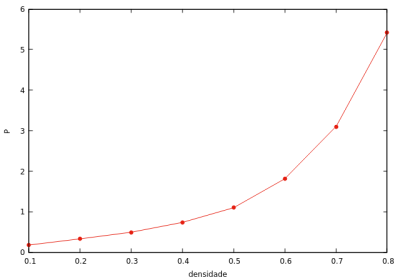
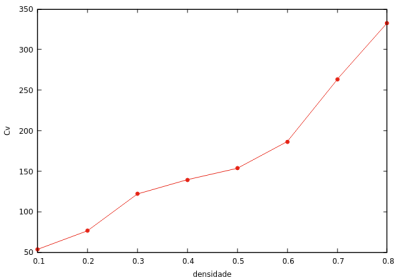
T = 2.0 (acima do valor crítico)
Nessa situação (acima do valor crítico de temperatura), o gráfico pressão - densidade (esquerda) mostra sua injetividade, e por tanto, a não coexistência de fases (como esperado). O gráfico capacidade térmica - densidade (direita) é monotonicamente crescente, por consequência.
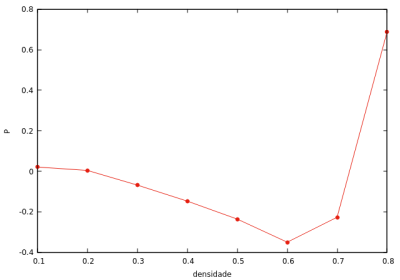
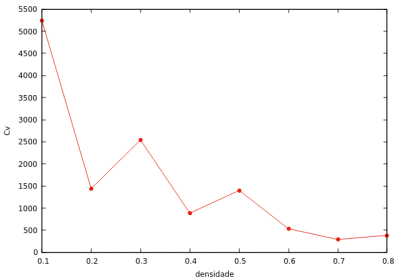
T = 0.9 (abaixo do valor crítico)
Nessa situação (abaixo do valor crítico de temperatura), o gráfico pressão - densidade (esquerda) mostra sua não-injetividade, e por tanto, a coexistência de fases líquido-vapor, apresentando metaestabilidade com pressões negativas na região. Esse efeito é devido ao tamanho pequeno da amostra, que tem um alto custo de energia livre para a criação de uma interface de vapor de líquido, por isso se torna pouco aconselhavel utilisar o ensemble NVT para diagramas de coexistência de fases.
Referências
- Cohen-Tannoudji C., Diu B., Laloe F. Quantum mechanics. Volume 1. Wiley, 1991.
- Numerical Resolution Of The Schrödinger Equation. Jorgensen L., Lopes Cardozo D., Thivierge E. http://web.pa.msu.edu/people/duxbury/courses/phy480/SchrodingerDynamics.pdf
- Crank, J.; Nicolson, P. (1947). "A practical method for numerical evaluation of solutions of partial differential equations of the heat conduction type". Proc. Camb. Phil. Soc. 43 (1): 50–67. doi:10.1007/BF02127704.
- Sherer, Philipp O.J., Computational Physics simulation of Classical and Quantum Systems. Springer, 2010.
- Born M., Nobel lecture: The statistical interpretation of quantum mechanics. 11 de Dezembro de 1954. https://www.nobelprize.org/nobel_prizes/physics/laureates/1954/born-lecture.pdf