Termostato de Andersen: mudanças entre as edições
| Linha 29: | Linha 29: | ||
<math> | <math></math> | ||
== TERMOSTATO DE ANDERSEN == | == TERMOSTATO DE ANDERSEN == | ||
Edição das 20h10min de 9 de dezembro de 2024
INTRODUÇÃO
A dinâmica molecular é uma técnica que naturalmente simula sistemas clássicos compostos por N partículas interagindo dentro de um volume V. Nesse contexto, as posições das partículas são atualizadas com base no potencial de interação escolhido. Sob a suposição de ergodicidade — ou seja, que as médias temporais equivalem às médias de ensemble —, as simulações resultam em amostragens do ensemble microcanônico (NVE). Nesse ensemble, o número de partículas N, o volume V, e a energia total E permanecem constantes (aproximadamente).
Ao colocar um sistema em contato com um reservatório térmico a uma temperatura T, mudamos do ensemble microcanônico (NVE), onde a energia é mantida constante, para o ensemble canônico (NVT), no qual a temperatura do sistema é constante. Nesse novo ensemble, a distribuição de probabilidade das velocidades das partículas segue a forma da distribuição de Maxwell-Boltzmann, uma distribuição gaussiana associada à temperatura T. Um dos métodos mais simples para realizar uma amostragem correta do ensemble canônico é o termostato de Andersen. Neste estudo, focaremos na análise desse termostato, explorando sua implementação, características e aplicação na simulação de sistemas termodinâmicos.
FUNDAMENTO TEÓRICO
Temperatura
A definição de temperatura em um sistema clássico em função das velocidades das partículas pode ser obtida pela equipartição de energia:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \frac{1}{2} m v_\alpha^2 \right\rangle = \frac{1}{2} k_B T }
Temos então:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T(t) = \frac{1}{k_B N_f} \sum_{i=1}^{N_f} m_i v_i^2}
onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_f} é o número de graus de liberdade do sistema. No ensemble microcanônico, como o momento é conservado, temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_f=3N-3} , mas no ensemble canônico, e portanto no termostato de Andersen, o momento não é conservado e utilizamos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_f=3N} .
Condições de Contorno Periódicas
As condições de contorno periódicas são fundamentais para garantir que simulações computacionais de sistemas físicos representem com precisão o comportamento de sistemas grandes e infinitos. Elas ajudam a evitar efeitos de borda que não são representativos do comportamento real de partículas em um espaço muito grande, permitindo simulações mais realistas e precisas.
É utilizada a convenção da imagem mínima, que calcula a menor distância entre as partículas, sendo essa sempre menor ou igual a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle L/2} .
Integração de Velocity-Verlet
Escolhido principalmente por não ser de ORDEM N² como o RK2, por exemplo. Precisamos calcular apenas 1 vez a força em cada passo do algoritmo. Assim, é o melhor "custo-benefício" dentre os possíveis algoritmos, tendo uma precisão razoável.
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle }
TERMOSTATO DE ANDERSEN
Para simular o contato do sistema com um reservatório térmico, a cada passo de tempo Δt é realizado um procedimento de Monte Carlo. Nesse processo, N partículas são selecionadas aleatoriamente, uma de cada vez, e suas velocidades são atualizadas. Essas novas velocidades são sorteadas a partir da distribuição gaussiana centrada em zero com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = \sqrt{T}} . Essa abordagem introduz um elemento de estocasticidade ao modelo, permitindo que a temperatura média do sistema oscile em torno da temperatura T do reservatório.
Na prática, a interação entre o sistema e o reservatório é controlada pela frequência de colisão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} . Para cada partícula, é gerado um número aleatório Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} no intervalo [0,1]. Caso Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r<\nu * \Delta t } a velocidade da partícula é atualizada conforme descrito.
Algoritmo
Podemos descrever o algoritmo em 4 passos:
1. Inicia-se com um conjunto de posições e velocidades.
2. Integra-se as equações do movimento para um passo Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta t} .
3. N partículas são selecionadas para colidir com o reservatório térmico.
4. Para cada partícula selecionada, definir nova velocidade a partir da distribuição de Maxwell-Boltzmann correspondente à temperatura T do reservatório.
RESULTADOS
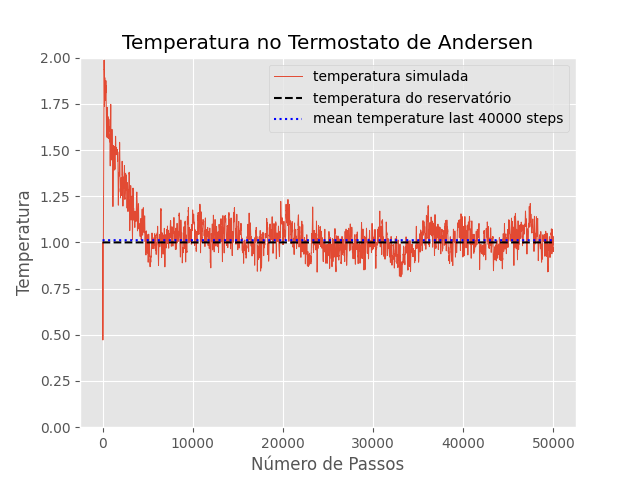
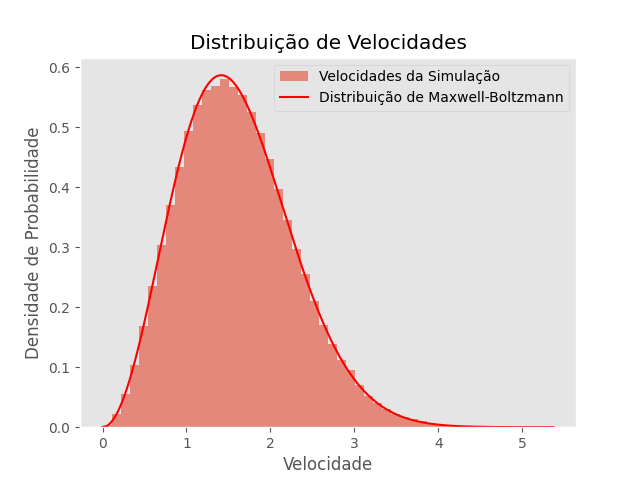
T=1 Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu = 1.011} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = 0.067}
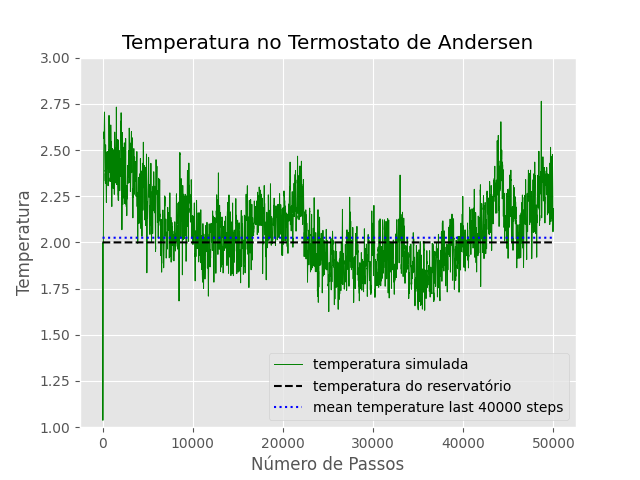
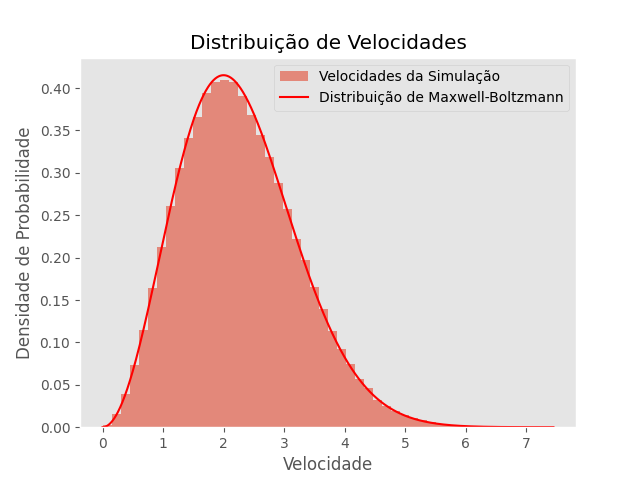
T=2
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu = 2.025}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = 0.166}
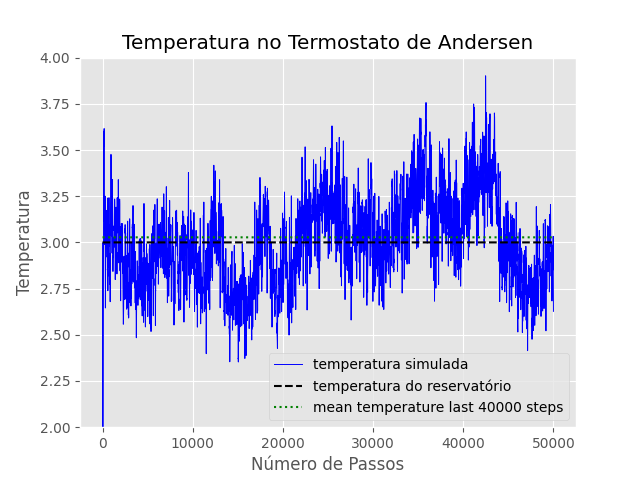
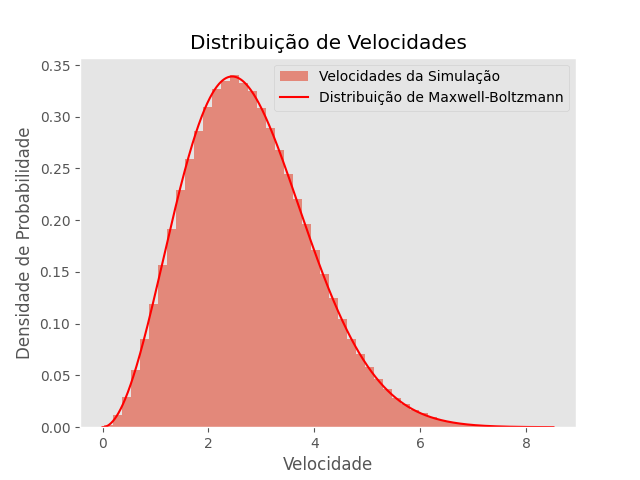
T=3
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu = 3.027}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = 0.247}