Grupo5 - Eq. Schroedinger: mudanças entre as edições
| (25 revisões intermediárias por 4 usuários não estão sendo mostradas) | |||
| Linha 16: | Linha 16: | ||
e as discretizações de <math>\frac{\partial \Psi}{\partial t}</math> (explícita e implícita, respectivamente): | e as discretizações de <math>\frac{\partial \Psi}{\partial t}</math> (explícita e implícita, respectivamente): | ||
<math>\frac{\ | <math>\frac{\partial \Psi}{\partial t} = \frac{\Psi^{n+1}_{j} - \Psi^{n}_{j}}{\Delta t}</math> (explícita) | ||
<math>\frac{\partial \Psi}{\partial t} = \frac{\Psi^{n}_{j} - \Psi^{n-1}_{j}}{\Delta t}</math> (implícita) | |||
O método de Crank-Nicolson consiste em uma média aritmética dos métodos explícito e implícito. Excetuando manipulações algébricas triviais, verifica-se que a relação de recorrência do método é dada por: | No método implícito as diferenças são tomadas no tempo <math> n+1 </math> ao invés de tomá-las no tempo <math> n </math> como no método explícito. | ||
<math>\frac{\Psi^{n+1}_{j} - \Psi^{n}_{j}}{\Delta t} = \frac{\Psi^{n+1}_{j+1} - 2\Psi^{n+1}_{j} + \Psi^{n+1}_{j-1}}{\left(\Delta x \right)^2}</math> | |||
fazendo <math>\lambda = \frac{\Delta t}{(\Delta x)^2}</math>, temos: | |||
<math>\Psi^{n}_{j} = - \lambda\Psi^{n+1}_{j+1} + (1 + 2 \lambda)\Psi^{n+1}_{j} - \lambda\Psi^{n+1}_{j-1}</math> | |||
Considerando <math>0 \leq j \leq M </math> temos <math> M - 1 </math> equações simultâneas. O método implícito converge à solução da EDP desde que <math> \Delta x \rightarrow 0 </math> e <math> \Delta t \rightarrow 0 </math> independente do valor de <math>\lambda</math>. | |||
Para obter os valores no dado tempo <math> n+1 </math> se resolve o conjunto de equações simultaneamente dado pela equação acima que pode ser escrita na forma matricial, | |||
:<math> | |||
\begin{pmatrix} | |||
-\lambda & (1+2\lambda) & -\lambda & \cdots & 0 & 0 & 0\\ 0 & -\lambda & (1+2\lambda) & -\lambda & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots& \vdots& \vdots \\ 0 & 0 & 0 & \cdots & -\lambda & (1+2\lambda) & -\lambda | |||
\end{pmatrix} | |||
\begin{pmatrix} \Psi_0^{n+1} \\ \Psi_1^{n+1} \\ \vdots \\ \Psi_{j-1}^{n+1}\end{pmatrix} | |||
= | |||
\begin{pmatrix} \Psi_0^{n} \\ \Psi_1^{n} \\ \vdots \\ \Psi_{j-1}^{n} \end{pmatrix} | |||
</math> | |||
Tanto no método explícito quanto no método implícito não é conservada a norma do estado (o que é estritamente necessário, já que o estado pode ser interpretado como uma onda de probabilidade). Por esse motivo, utiliza-se o método de Crank-Nicolson, o qual tem essa propriedade. | |||
O método de Crank-Nicolson consiste em uma média aritmética dos métodos explícito e implícito. Essa combinação dá a estabilidade do método implícito e a precisão do método explícito, apesar de causar oscilações numéricas (podendo ser contornadas usando passos de tempo menores). Excetuando manipulações algébricas triviais, verifica-se que a relação de recorrência do método é dada por: | |||
<math>a\Psi^{n+1}_{j-1} + b_{j}\Psi^{n+1}_{j} + a\Psi^{n+1}_{j+1} = a^* \Psi^{n}_{j-1} + b_{j}^{*} \Psi^{n}_{j} + a^*\Psi^{n}_{j+1},</math> | <math>a\Psi^{n+1}_{j-1} + b_{j}\Psi^{n+1}_{j} + a\Psi^{n+1}_{j+1} = a^* \Psi^{n}_{j-1} + b_{j}^{*} \Psi^{n}_{j} + a^*\Psi^{n}_{j+1},</math> | ||
| Linha 66: | Linha 89: | ||
==Implementação em C== | ==Implementação em C== | ||
| Linha 72: | Linha 95: | ||
<source lang="c"> | <source lang="c"> | ||
#include <stdio.h> | |||
#include <math.h> | |||
#include <complex.h> | |||
#define N_steps 100000 | |||
#define L 1000 | |||
#define dt 1 | |||
#define dx 4.0 | |||
#define w 0.002 | |||
double V(int x_rel) | |||
{ | { | ||
/ | return - pow(w,2) * pow(x_rel - 500,2) / 2.0; //SHO | ||
// | //return 0; | ||
} | |||
// | double complex b(int i) | ||
{ | |||
return 0.5 * dt * I * (1.0 / pow(dx,2.0) + V(i)) + 1.0; | |||
} | |||
double u_0(int x_rel) | |||
{ | |||
//return sqrt(2 / L) * sin(5*x_rel * M_PI / L); //eigenstate of infinite square well | |||
//return (1.0/ sqrt(5 * M_PI)) * exp(I * 0.5 * x_rel) * exp(-pow(x_rel - 500, 2) / (2 * 25)); //gaussian packet | |||
return (w / M_PI) * exp(-w * pow(x_rel - 500, 2) / 2.0); | |||
} | |||
void CN(double complex *u, double complex *u_aux, double complex *u_next, double complex a, int bi) | |||
{ | |||
//bi = 1 (bounded); bi = 0 (periodic) | |||
int i; | int i; | ||
for(i = bi; i <= L - bi; i++) u_aux[i] = conj(a) * (u[(i-1+L)%L] + u[(i+1+L)%L]) + conj(b(i)) * u[i]; | |||
//thomas algorithm | |||
// | |||
double complex c_new[L+1], d_new[L+1]; | double complex c_new[L+1], d_new[L+1]; | ||
c_new[ | c_new[bi] = a / b(bi); | ||
for(i = | for(i = 1 + bi; i <= L - bi; i++) c_new[i] = a / (b(i) - c_new[i-1] * a); | ||
d_new[ | d_new[bi] = u_aux[bi] / b(bi); | ||
for(i = | for(i = 1 + bi; i <= L - bi; i++) d_new[i] = (u_aux[i] - d_new[i-1] * a) / (b(i) - c_new[i-1] * a); | ||
u_next[0] = u_next[L] = 0; | if (bi == 1) u_next[0] = u_next[L] = 0; | ||
u_next[L- | u_next[L-bi] = d_new[L-bi]; | ||
for(i = L- | for(i = L-1-bi; i >= bi; i --) u_next[i] = d_new[i] - c_new[i] * u_next[i+1]; | ||
// | //u = u_next | ||
for(i = 0; i <= L; i++) u[i] = u_next[i]; | for(i = 0; i <= L; i++) u[i] = u_next[i]; | ||
} | } | ||
int main(void) | |||
{ | |||
int i, j, n = 0; | |||
double complex u[L+1], u_next[L+1], u_aux[L+1], a = - 0.25 * I * dt / pow(dx,2.0); | |||
//Initial Contition | |||
for(i = 0; i <= L; i ++) u[i] = u_0(i); | |||
while(n < N_steps) | |||
{ | |||
CN(u, u_aux, u_next, a, 0); | |||
printf("set title 'Time = %d'\nplot \'-' w lp pt 7 ps 0.1", n); | |||
for(i = 0; i <= L; i ++) printf("%d\t%.10lf\n",i,pow(creal(u[i]),2) + pow(cimag(u[i]),2)); | |||
//for(i = 0; i <= L; i ++) printf("%d\t%lf\n",i,cimag(u[i])); | |||
//for(i = 0; i <= L; i ++) printf("%d\t%lf\n",i,creal(u[i])); | |||
printf("e\npause 0.1\n"); | |||
n ++; | |||
} | |||
return 0; | |||
} | |||
</source><br /> | </source><br /> | ||
==Aplicações== | |||
===Linearidade da função de onda=== | |||
[[Arquivo:gaussian_sho.gif]] | |||
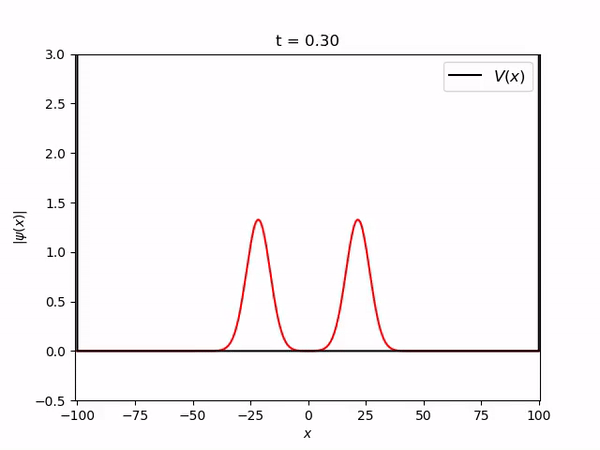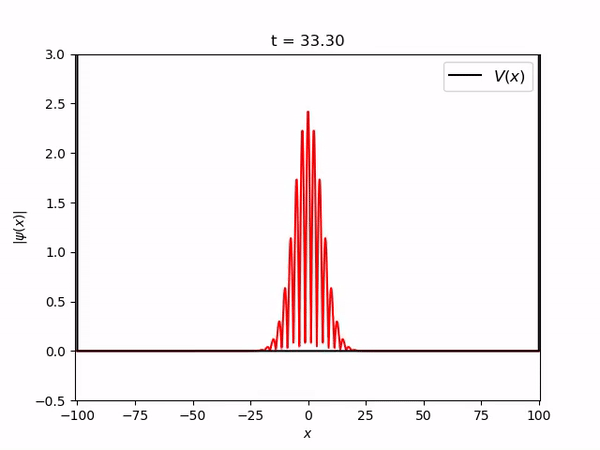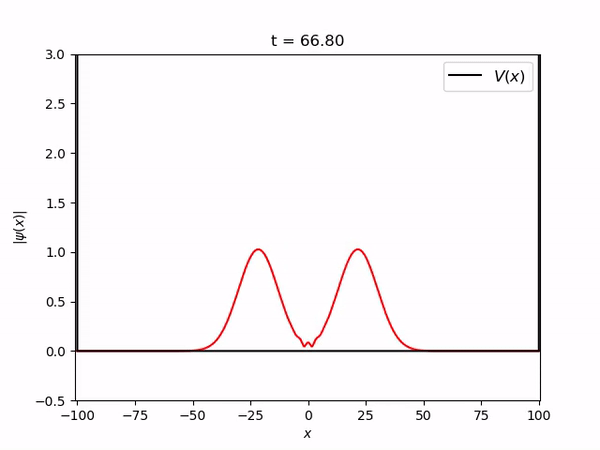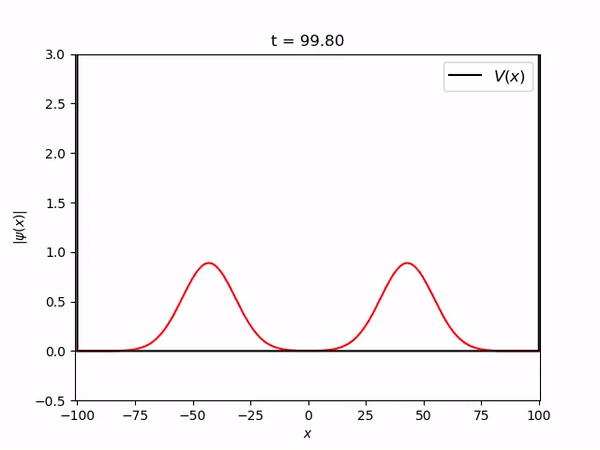
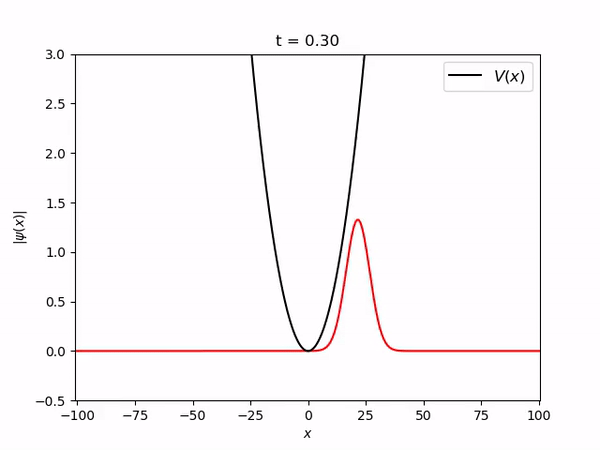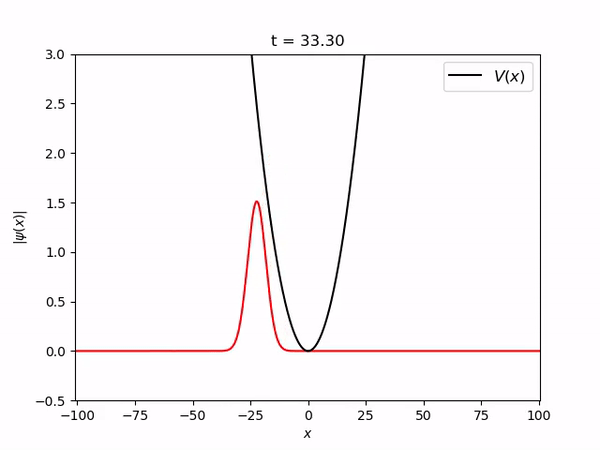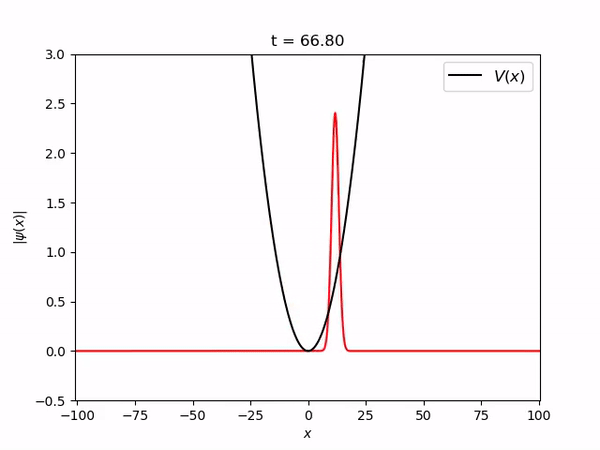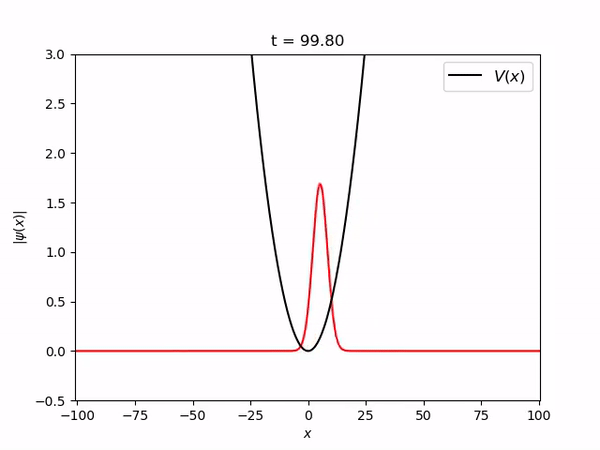
===Pacote gaussiano estacionário num oscilador harmônico=== | |||
[[Arquivo:gaussian_linearity.gif]] | |||
===Pacote gaussiano tunelando uma berreira de potencial=== | |||
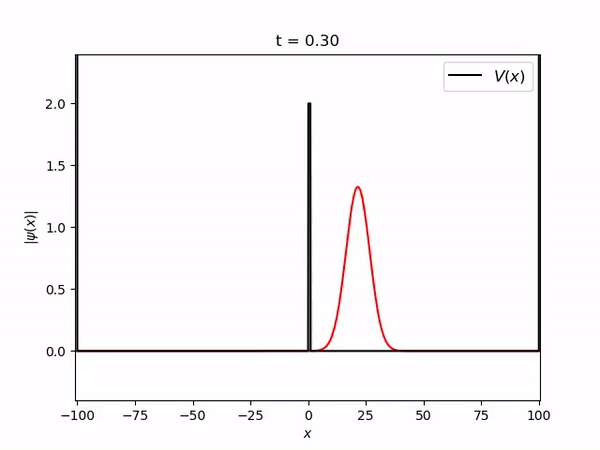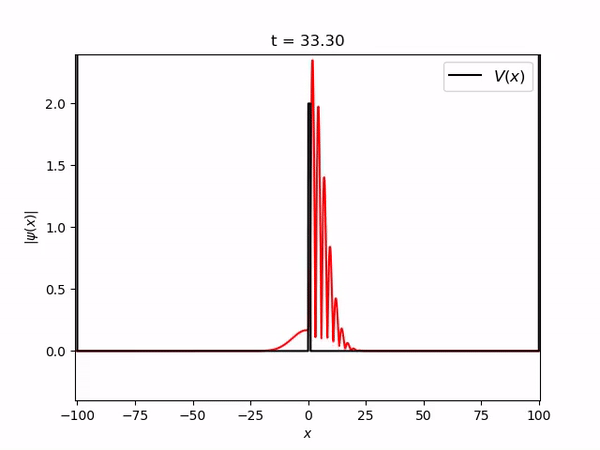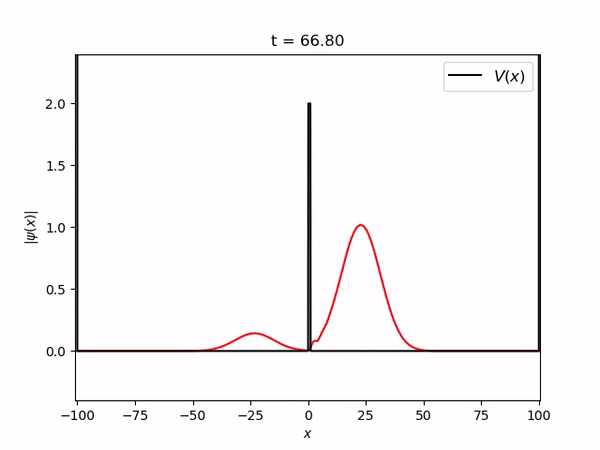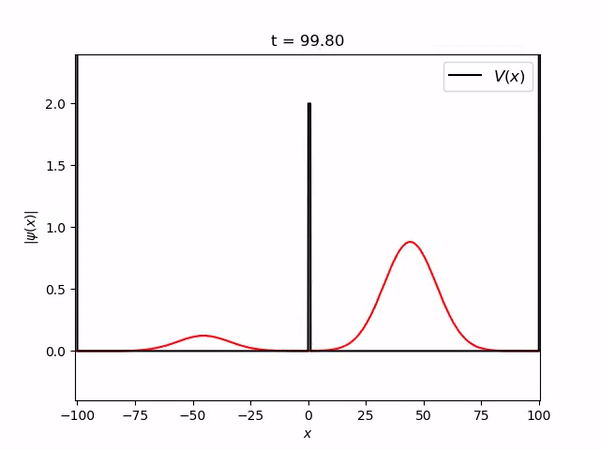
[[Arquivo:gaussian_barrier.gif]] | |||
==Referências== | ==Referências== | ||
*Cohen-Tannoudji C., Diu B., Laloe F. Quantum mechanics. Volume 1. Wiley, 1991. | *Cohen-Tannoudji C., Diu B., Laloe F. Quantum mechanics. Volume 1. Wiley, 1991. | ||
*Numerical Resolution Of The Schrödinger Equation. Jorgensen L., Lopes Cardozo D., Thivierge E. http://web.pa.msu.edu/people/duxbury/courses/phy480/SchrodingerDynamics.pdf | *Numerical Resolution Of The Schrödinger Equation. Jorgensen L., Lopes Cardozo D., Thivierge E. http://web.pa.msu.edu/people/duxbury/courses/phy480/SchrodingerDynamics.pdf | ||
*Crank, J.; Nicolson, P. (1947). "A practical method for numerical evaluation of solutions of partial differential equations of the heat conduction type". Proc. Camb. Phil. Soc. 43 (1): 50–67. doi:10.1007/BF02127704. | |||
*Sherer, Philipp O.J., Computational Physics simulation of Classical and Quantum Systems. Springer, 2010. | *Sherer, Philipp O.J., Computational Physics simulation of Classical and Quantum Systems. Springer, 2010. | ||
*Born M., Nobel lecture: The statistical interpretation of quantum mechanics. 11 de Dezembro de 1954. https://www.nobelprize.org/nobel_prizes/physics/laureates/1954/born-lecture.pdf | |||
Edição atual tal como às 12h52min de 17 de janeiro de 2018
A evolução temporal do estado quântico é dada pela equação de Schrödinger, a qual é postulada como:
Posto em unidades atômicas (onde e são unitários), o caso unidimensional de um elétron num potencial independente do tempo reduz-se a:
Método numérico
Buscando resolver a equação numericamente, tem-se a discretização de :
e as discretizações de (explícita e implícita, respectivamente):
(explícita)
(implícita)
No método implícito as diferenças são tomadas no tempo ao invés de tomá-las no tempo como no método explícito.
fazendo , temos:
Considerando temos equações simultâneas. O método implícito converge à solução da EDP desde que e independente do valor de .
Para obter os valores no dado tempo se resolve o conjunto de equações simultaneamente dado pela equação acima que pode ser escrita na forma matricial,
Tanto no método explícito quanto no método implícito não é conservada a norma do estado (o que é estritamente necessário, já que o estado pode ser interpretado como uma onda de probabilidade). Por esse motivo, utiliza-se o método de Crank-Nicolson, o qual tem essa propriedade.
O método de Crank-Nicolson consiste em uma média aritmética dos métodos explícito e implícito. Essa combinação dá a estabilidade do método implícito e a precisão do método explícito, apesar de causar oscilações numéricas (podendo ser contornadas usando passos de tempo menores). Excetuando manipulações algébricas triviais, verifica-se que a relação de recorrência do método é dada por:
onde
e .
A integração numérica depende, portanto, do potencial em que o elétron está sujeito, bem como da sua condição inicial e suas das condições de contorno.
Que condições podemos impor para a fronteira? Quando se trata do problema analiticamente, costuma-se considerar que a função de onda tende a zero no infinito. Numericamente, pode-se fazer uma transposição disso, criando uma condição para bordas em pontos suficientemente distantes do centro da distribuição da função de onda, igualando-as a zero. Outra forma de tratar o problema numericamente é criando condições de contorno periódicas, em que para as bordas vale para todo (ou, para as bordas e há a relação para todo ).
Condições de contorno iguais a zero
Para as condições de contorno , a iteração reduz-se à equação matricial:
Condições de contorno periódicas
De maneira semelhante, a iteração do caso das condições de contorno periódicas - - reduz-se à equação matricial:
Condição inicial
Já a condição inicial é arbitrária, pois define o estado inicial do sistema que queremos tratar. Fazendo uma referência ao tratamento de sistemas clássicos, seria como definir posição e momento iniciais. É claro que, para ter o sentido físico de uma função de onda, deve-se ter o cuidado de criar uma condição inicial normalizada, satisfazendo
bastando, então, inseri-la no programa.
Implementação em C
#include <stdio.h>
#include <math.h>
#include <complex.h>
#define N_steps 100000
#define L 1000
#define dt 1
#define dx 4.0
#define w 0.002
double V(int x_rel)
{
return - pow(w,2) * pow(x_rel - 500,2) / 2.0; //SHO
//return 0;
}
double complex b(int i)
{
return 0.5 * dt * I * (1.0 / pow(dx,2.0) + V(i)) + 1.0;
}
double u_0(int x_rel)
{
//return sqrt(2 / L) * sin(5*x_rel * M_PI / L); //eigenstate of infinite square well
//return (1.0/ sqrt(5 * M_PI)) * exp(I * 0.5 * x_rel) * exp(-pow(x_rel - 500, 2) / (2 * 25)); //gaussian packet
return (w / M_PI) * exp(-w * pow(x_rel - 500, 2) / 2.0);
}
void CN(double complex *u, double complex *u_aux, double complex *u_next, double complex a, int bi)
{
//bi = 1 (bounded); bi = 0 (periodic)
int i;
for(i = bi; i <= L - bi; i++) u_aux[i] = conj(a) * (u[(i-1+L)%L] + u[(i+1+L)%L]) + conj(b(i)) * u[i];
//thomas algorithm
double complex c_new[L+1], d_new[L+1];
c_new[bi] = a / b(bi);
for(i = 1 + bi; i <= L - bi; i++) c_new[i] = a / (b(i) - c_new[i-1] * a);
d_new[bi] = u_aux[bi] / b(bi);
for(i = 1 + bi; i <= L - bi; i++) d_new[i] = (u_aux[i] - d_new[i-1] * a) / (b(i) - c_new[i-1] * a);
if (bi == 1) u_next[0] = u_next[L] = 0;
u_next[L-bi] = d_new[L-bi];
for(i = L-1-bi; i >= bi; i --) u_next[i] = d_new[i] - c_new[i] * u_next[i+1];
//u = u_next
for(i = 0; i <= L; i++) u[i] = u_next[i];
}
int main(void)
{
int i, j, n = 0;
double complex u[L+1], u_next[L+1], u_aux[L+1], a = - 0.25 * I * dt / pow(dx,2.0);
//Initial Contition
for(i = 0; i <= L; i ++) u[i] = u_0(i);
while(n < N_steps)
{
CN(u, u_aux, u_next, a, 0);
printf("set title 'Time = %d'\nplot \'-' w lp pt 7 ps 0.1", n);
for(i = 0; i <= L; i ++) printf("%d\t%.10lf\n",i,pow(creal(u[i]),2) + pow(cimag(u[i]),2));
//for(i = 0; i <= L; i ++) printf("%d\t%lf\n",i,cimag(u[i]));
//for(i = 0; i <= L; i ++) printf("%d\t%lf\n",i,creal(u[i]));
printf("e\npause 0.1\n");
n ++;
}
return 0;
}
Aplicações
Linearidade da função de onda
Pacote gaussiano estacionário num oscilador harmônico
Pacote gaussiano tunelando uma berreira de potencial
Referências
- Cohen-Tannoudji C., Diu B., Laloe F. Quantum mechanics. Volume 1. Wiley, 1991.
- Numerical Resolution Of The Schrödinger Equation. Jorgensen L., Lopes Cardozo D., Thivierge E. http://web.pa.msu.edu/people/duxbury/courses/phy480/SchrodingerDynamics.pdf
- Crank, J.; Nicolson, P. (1947). "A practical method for numerical evaluation of solutions of partial differential equations of the heat conduction type". Proc. Camb. Phil. Soc. 43 (1): 50–67. doi:10.1007/BF02127704.
- Sherer, Philipp O.J., Computational Physics simulation of Classical and Quantum Systems. Springer, 2010.
- Born M., Nobel lecture: The statistical interpretation of quantum mechanics. 11 de Dezembro de 1954. https://www.nobelprize.org/nobel_prizes/physics/laureates/1954/born-lecture.pdf

![{\displaystyle i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,t)=\left[-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}+V(\mathbf {r} ,t)\right]\Psi (\mathbf {r} ,t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4f4ed7764bdfd41744d5dc7d6bb8e424eed9f78)


![{\displaystyle {\frac {\partial }{\partial t}}\Psi (x,t)=\left[{\frac {i}{2}}{\frac {\partial ^{2}}{\partial x^{2}}}-iV(x)\right]\Psi (x,t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe0e5089dff6294c3f2f642acbd48b06dbf5ca88)


















![{\displaystyle b_{j}\equiv 1+{\frac {i\Delta t}{2}}\left[{\frac {1}{(\Delta x)^{2}}}+V(j\Delta x)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65f521dd672396892e351759cfb730f4475f17ed)