Grupo4 - FFT: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| (15 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
A Transformada rápida de Fourier (em inglês '''Fast Fourier Transform''', ou '''FFT''') é um algoritmo que torna o cálculo da Transformada Discreta de Fourier (DFT) | A Transformada rápida de Fourier (em inglês '''Fast Fourier Transform''', ou '''FFT''') é um algoritmo que torna viável o cálculo da Transformada Discreta de Fourier (DFT), que é a forma discretizada da [[https://pt.wikipedia.org/wiki/Transformada_de_Fourier Transformada de Fourier]]. | ||
A '''FFT''' permite transformar de forma rápida uma série de sinais discretos em uma amostra contendo as frequências desses sinais, desde que satisfaça algumas propriedades. | |||
| Linha 16: | Linha 18: | ||
A transformada também pode ser expressa em forma vetorial, como | A transformada também pode ser expressa em forma vetorial, como | ||
<math>\vec{ | <math>\vec{A} = \mathbf{W^{nk}} \vec{a} ~ </math> onde <math> ~ \mathbf{W^{nk}} ~ </math> é definido como | ||
<math>\mathbf{W^{nk}} = \begin{bmatrix} | <math>\mathbf{W^{nk}} = \begin{bmatrix} | ||
| Linha 26: | Linha 29: | ||
O cálculo dessa expressão leva em torno de <math>N^2</math> passos para o resultado. Uma amostra com 3,000 pontos precisa de 9,000,000 operações para a transformada ser obtida, tornando a DFT inviável para aplicações rápidas. | O cálculo dessa expressão leva em torno de <math>N^2</math> passos para o resultado. Uma amostra com 3,000 pontos precisa de 9,000,000 operações para a transformada ser obtida, tornando a DFT inviável para aplicações rápidas. | ||
== Transformada Rápida de Fourier == | == Transformada Rápida de Fourier == | ||
| Linha 95: | Linha 97: | ||
onde | onde | ||
<math>n = n_1 \cdot r_2 + n_0</math> , <math> | <math>k = k_1 \cdot r_1 + k_0 ~~~~~~~~ k_0 = 0,1,...,r_1-1 ~~~~~~~~ k_1 = 0,1,...,r_2-1</math> | ||
<math>n = n_1 \cdot r_2 + n_0 ~~~~~~~~ n_0 = 0,1,...,r_2-1 ~~~~~~~~ n_1 = 0,1,...,r_1-1</math> | |||
assim a transformada que antes necessitava de N cálculos, agora pode ser vista como <math>r_1 + r_2</math> cálculos. | |||
Uma outra alternativa para o calculo da FFT é adicionar pontos 0 no fim da sequência. Por exemplo, para uma FFT de 5 pontos, basta adicionar 3 pontos 0 e calcular uma FFT pelos métodos já mostrados. Uma dificuldade dessa alternativa é que a transformada terá também 8 pontos, e apesar de corresponder ao mesmo formato da função original, está amostrada numa frequência diferente. | |||
=== Algorítmo (usando recursão) === | |||
<math>>>\mathbf{function} ~ FFT(N,\vec{a})</math> | |||
<math> >>> ~~~~ \mathbf{if} ~ N = 1 ~ \mathbf{then}</math> | |||
<math> >>> ~~~~~~~~ return ~ \vec{a};</math> | |||
<math> >>> ~~~~ \mathbf{else}</math> | |||
<math> >>>~~~~~~~~ E = FFT(N/2, (a_0, a_2, ..., a_{N-2}));</math> | |||
<math> >>>~~~~~~~~ O = FFT(N/2, (a_1, a_3, ..., a_{N-1}));</math> | |||
<math> >>>~~~~~~~~ \mathbf{for} ~ k = 0 ~ to ~ k <= N/2 -1 ~ \mathbf{do}</math> | |||
<math> >>>~~~~~~~~~~~~ A_k=E_k+exp(-i2\pi k/N) * O_k;</math> | |||
<math> >>>~~~~~~~~~~~~ A_{k+N/2}=E_k-exp(-i2\pi k/N) * O_k;</math> | |||
<math> >>>~~~~ return ~ \vec{A};</math> | |||
== Implementação == | |||
A natureza recursiva do algoritmo da transformada rápida de fourier o torna ideal para implementações em linguagens funcionais como Haskell. Abaixo exibimos as partes mais relevantes do código, onde omitimos inclusões de bibliotecas e a definição das funções auxiliares evens e odds. | |||
<source lang="haskell" line='line'> | |||
--esse termo multiplica o somatório de termos ímpares | |||
f xs n = exp $ -(0:+2*pi)*n / genericLength xs | |||
--caso a função seja chamada com apenas dois termos, temos o caso base | |||
ffti [x,y] n = x + y * (exp $ -(0:+pi)*n) | |||
--caso contrário aplique a função recursivamente separando o somatório em | |||
-- termos com índice par e com índice ímpar | |||
ffti xs n = ffti (evens xs) n + f xs n * ffti (odds xs) n | |||
--função que calcula os n coeficientes (ffti calcula um coeficiente) | |||
fft xs [] = [] | |||
fft xs (y:ys) = (ffti xs y):(fft xs ys) | |||
--exemplo | |||
fft [0, 1, 4, 9] [0,1,2,3] | |||
--saída ( :+ indica número complexo em Haskell) | |||
[14.0 :+ 0.0, -4.0 :+ 8.0, -6.0 :+ 0.0, -4.0 :+ -8.0)] | |||
</source> | |||
Embora não seja uma linguagem puramente funcional Wolfram Mathematica também se presta a uma implementação direta e clara. | |||
<source lang="css" line='line'> | |||
// caso base de uma lista contendo apenas dois termos | |||
fft[{x_, y_}, n_] := x + y Exp[-I Pi n ] | |||
// caso contrário, divida a lista entre termos com índice ímpar e par | |||
// e aplique a função recursivamente | |||
fft[f_List, n_] := fft[Downsample[f, 2, 1], n] + | |||
Exp[-((I 2 Pi n )/Length[f])] fft[Downsample[f, 2, 2], n] | |||
//acima calcula-se com um coeficiente abaixo calcula-se todos | |||
fft[f_List] := Table[fft[f, n] // N, {n, 0, Length[f] - 1}] | |||
//exemplo | |||
fft[{0, 1, 4, 9}] | |||
{14., -4. + 8. I, -6., -4. - 8. I} | |||
</source> | |||
== Exemplos == | |||
Abaixo encontra-se alguns exemplos básicos da transformada de fourier com base no código acima porém com modificações para lidar com o caso em que o intervalo de amostragem é diferente de <math>[0, 2\pi]</math> e cuja taxa de amostragem é qualquer (diferente de <math>\frac{2\pi k}{N}</math> como assumido acima) | |||
=== Gaussiana === | |||
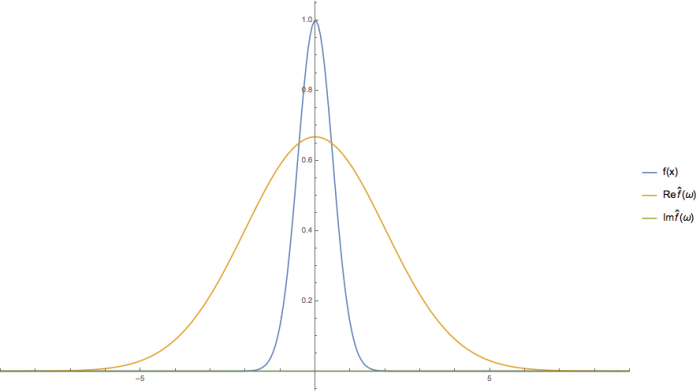
A menos de uma normalização a função gaussiana é definida por: <math>f(x) = e^{-\frac{(x - <x>)^2}{2 \sigma^2}}</math> | |||
Aplicando a transformada de fourier na curva gaussiana obtem-se outra gaussiana. | |||
[[Arquivo:gaussian1.png|700px]] | |||
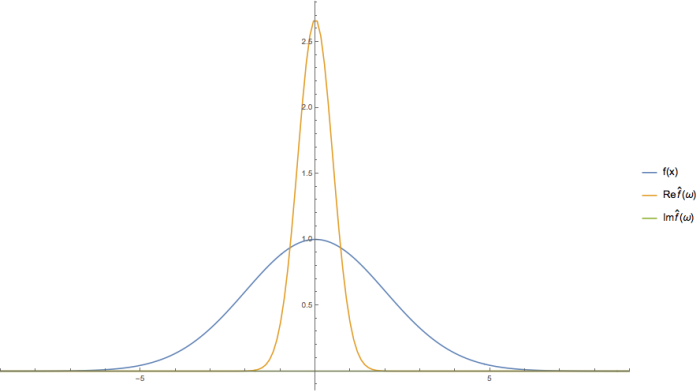
Observa-se que uma curva larga no espaço real corresponde a uma curva estreita no espaço de fourier e vice-versa. Esse é um fato matemático amplamente conhecido e se exprime também na física pelo Princípio da Incerteza de Heisenberg. | |||
Abaixo uma curva gaussiana mais larga que a anterior e sua transformada correspondentemente mais estreita. | |||
[[Arquivo:gaussian2.png|700px]] | |||
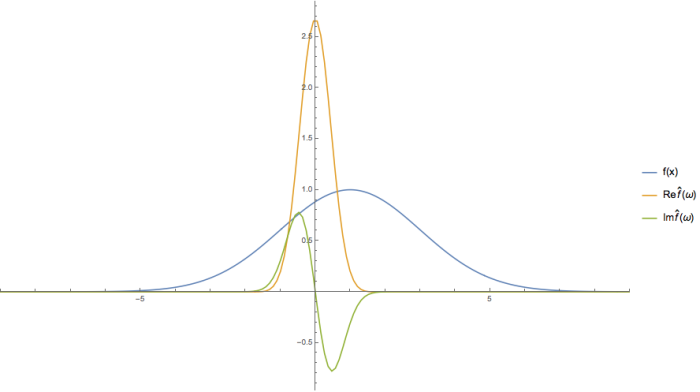
Uma função par em relação à origem possui uma expansão em fourier com termos ímpares nulos, no entanto, deslocando a gaussiana um pouco para a direita e, portanto, quebrando sua simetria, vemos que a sua transformada possui uma parte complexa: | |||
[[Arquivo:gaussian3.png|700px]] | |||
=== Oscilador Harmônico Amortecido === | |||
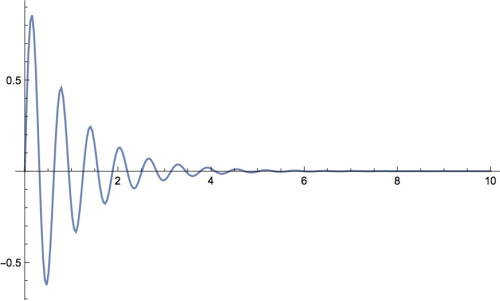
A curva que representa um oscilador harmônico amortecido é descrita por <math>f(x) = sin(a x) e^{-bx}</math> onde o termo senoidal, periódico, é amortecido pelo termo exponencial que leva a oscilação rapidamente a zero. | |||
[[Arquivo:osch.jpg|500px]] | |||
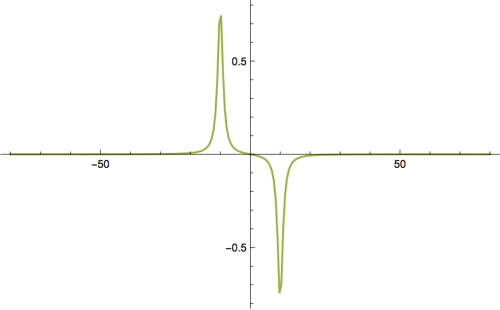
A transformada de fourier dessa curva possui parte real e imaginária, da parte imaginária dessa curva é possível obter a frequência de ressonância do fenômeno representado por ela. No caso abaixo vemos que a frequência de ressonância vale <math>\pm 10Hz</math> | |||
[[Arquivo:oschim.png|500px]] | |||
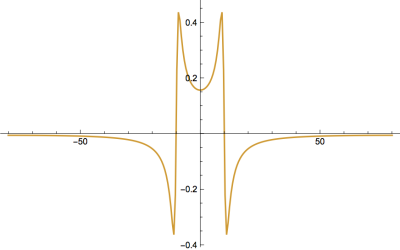
Abaixo a parte real da transformada: | |||
[[Arquivo:oschre.png|400px]] | |||
== Aplicações == | |||
=== Equação de Schrödinger: propagação de onda de probabilidade === | |||
O cálculo da evolução temporal da equação de schrödinger é computacionalmente exigente. A cada passo de tempo é necessário recalcular a posição da onda de probabilidade que representa a partícula em cada ponto do domínio. Portanto, torna-se vantajoso o uso da transformada de fourier rápida. Além disso a própria transformada faz parte da solução, pois também deseja-se obter a sua evolução temporal no espaço de momento. O código foi desenvolvido em python por [https://jakevdp.github.io/blog/2012/09/05/quantum-python/ Jake Vanderplas], no entanto, sob extensas modificações foi possível não apenas entender o código mas também modifica-lo para representar situações diferentes das propostas pelo autor. No site do autor encontra-se a explicação da teoria por trás do problema e também o funcionamento do algoritmo. A seguir exploramos a interação de uma onda de probabilidade com potenciais de diferentes formas. | |||
A parte principal do código modificado é exibida abaixo. Nota-se que o autor utilizou o método Leapfrog para integrar as equações de movimento fazendo a seguinte sequência de operações: dar um meio passo no espaço real, tomar a transformada, dar um passo no espaço de momento, tomar a transformada inversa e finalmente dar um passo completo no espaço real. | |||
<source lang="python" line='line'> | |||
def time_step(): | |||
global t, psi_mod_x, psi_mod_k, t_max | |||
psi_mod_x *= x_evolve_half | |||
for i in range(N_steps): | |||
psi_mod_k = fft(psi_mod_x) | |||
psi_mod_k *= k_evolve | |||
psi_mod_x = ifft(psi_mod_k) | |||
psi_mod_x *= x_evolve_half*x_evolve_half | |||
psi_mod_k = fft(psi_mod_x) | |||
t += dt * N_steps | |||
t_max = t_max - 1 | |||
</source> | |||
O restante do código ocupa-se somente de inicialização de valores, definição do potencial e escrita dos resultados. | |||
==== Potencial Quadrado ==== | |||
O potencial quadrado foi o exemplo escolhido pelo autor do código. Nesse exemplo fica visível que uma porção da onda de probabilidade atravessa o potencial embora classicamente não tenha energia suficiente para tal feito. Essa é uma demonstração numérica do efeito de tunelamento. | |||
[[Arquivo:Square.gif]] | |||
==== Potencial Triangular ==== | |||
O potencial triangular, por ter uma base mais larga, coíbe o efeito de tunelamento, no entanto, uma pequena porção da onda incidente ainda consegue transpor a barreira. | |||
[[Arquivo:Triangular.gif]] | |||
==== Potencial Batman ==== | |||
Em cursos básicos de quântica normalmente resolve-se apenas o potencial quadrado, às vezes, excepcionalmente, apresenta-se o potencial triangular. Isso se deve a dificuldade em tratar casos de potenciais irregulares analiticamente. Mas em casos reais os potenciais são extremamente irregulares. A solução numérica trata tais casos com naturalidade e sem qualquer alteração. Em particular, um potencial tipo batman é encarado sem problemas: | |||
[[Arquivo:Batman.gif]] | |||
A parte superior da curva é apenas ilustrativa (pois não faz sentido matemático nem físico) | |||
=== Padrões de Difração === | |||
A transformada rápida é muito utilizada no tratamento de imagens. Software como ImageJ ou Matlab possuem muitas ferramentas que fazem uso da técnica. Uma aplicação específica da FFT é na análise de imagens de partículas nanométricas obtidas por um microscópio eletrônico de transmissão. Esse equipamento produz um interferograma que (a menos de correções) representa a imagem real do que se está observando mas também produz uma segunda imagem, localizada no ponto focal da lente, que é o padrão de difração da imagem real. Essa imagem é uma visualização do espaço recíproco, ou seja, da transformada do espaço real. | |||
Abaixo está uma imagem de um plano de átomos de ouro obtida por um microscópio de transmissão eletrônica com uma escala de 2 nanômetros na qual destacamos uma região (quadrado vermelho) na qual tomaremos a transformada de fourier. A imagem em si é representada por uma matrix 800x800 onde cada elemento da matrix é um valor de intensidade sendo 0 para totalmente escuro e 255 para totalmente claro. | |||
[[Arquivo:Region.png|600px]] | |||
Utilizando, por exemplo o software Matlab podemos tomar a transformada inversa dessa imagem. A transformada de fourier produz o padrão de difração que revela a periodicidade da imagem. | |||
O código em Matlab é bem simples: | |||
<source lang="python" line='line'> | |||
function imagefft(I) | |||
F = fft2(I); | |||
F = fftshift(F); % centraliza a FFT | |||
F = abs(F); % obtem a magnitude (desnecessário, nossa imagem varia de 0 a 255) | |||
F = log(F+1); % escala logaritmica, +1 por que log(0) é indefinido | |||
F = mat2gray(F); % renormaliza a imagem de 0-255 para 0-1 | |||
imshow(F,[]) % exibe o resultado | |||
end | |||
</source> | |||
[[Arquivo:Matlab fft.png|600px]] | |||
Cada par de pontos simétricos em relação ao ponto central representa um conjunto de planos paralelos no espaço real, sendo a imagem real o conjunto de todos os planos representados por todos os pontos somado ao ruído da imagem. Observe que a imagem original, além de ruído, apresenta três planos diferentes como pode-se notar pela orientação dos átomos. Isso explica a presença de linhas claras ao redor dos pontos de difração. Um cristal perfeito, por outro lado, possuiria um padrão de difração de pontos localizados e não discos com linhas como vemos num cristal real. | |||
A seguir vejamos como decompor essas informações. Aplicando uma máscara sobre a imagem podemos selecionar apenas um par de pontos e ver a qual conjunto de planos do espaço real ele está relacionado: | |||
[[Arquivo:Applied mask.png|900px]] | |||
Para descobrir qual é o conjunto de planos tomamos a transformada inversa: | |||
[[Arquivo:Inverse fft.png|900px]] | |||
Como mencionado se selecionarmos todos os pontos e tomarmos a transformada inversa obteremos a imagem original, no entanto, removendo boa parte dos ruídos - a parte que deixamos de fora da máscara. | |||
[[Arquivo:Full mask.png|900px]] | |||
[[Arquivo:Removed all noise.png|900px]] | |||
Se quisermos ver a composição do ruído podemos tomar a máscara inversa e aplicar a transformada inversa, obtendo: | |||
[[Arquivo:Negative mask.png|900px]] | |||
[[Arquivo:Noise.png|900px]] | |||
== Referências Bibliográficas== | |||
[1] [https://web.stanford.edu/class/cme324/classics/cooley-tukey.pdf An Algorithm for the Machine Calculation of. Complex Fourier Series. By James W. Cooley and John W. Turkey]. | |||
[2] Kreyszig, Erwin. Advanced Engineering Mathematics. Wiley, 2011. | |||
[3] Scherer, Claudio. Métodos Computacionais da Física. | |||
[4] Richard; Faires, Douglas. Numerical Analysis, 2011 | |||
Edição atual tal como às 23h35min de 28 de janeiro de 2018
A Transformada rápida de Fourier (em inglês Fast Fourier Transform, ou FFT) é um algoritmo que torna viável o cálculo da Transformada Discreta de Fourier (DFT), que é a forma discretizada da [Transformada de Fourier]. A FFT permite transformar de forma rápida uma série de sinais discretos em uma amostra contendo as frequências desses sinais, desde que satisfaça algumas propriedades.
Transformada Discreta de Fourier
Em muitas aplicações se tem informação sobre um conjunto de dados, ao invés de uma função contínua. A Transformada Discreta de Fourier transforma esse conjunto de dados em um conjunto de tamanho igual com informação sobre as frequências da função que satisfaz o conjunto de dados.
Para um conjunto de dados igualmente espaçados, pode-se, ao considerar os dados como um período de uma função periódica, cujo período normalmente é considerado entre Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle [-\pi, \pi]} para facilitar o cálculo (e que pode sempre ser transformada em uma função nesse interválo), mostrar que a transformada discreta de Fourier pode ser dada pela equação:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_k = \sum_{n=0}^{N-1} f_n e^{-i2\pi nk/N}}
A sua inversa é, em paralelo ao caso da transformada contínua,
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_n = \frac{1}{N} \sum_{n=0}^{N-1} F_k e^{i2\pi nk/N}}
A transformada também pode ser expressa em forma vetorial, como
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{A} = \mathbf{W^{nk}} \vec{a} ~ } onde Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle ~ \mathbf{W^{nk}} ~ } é definido como
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{W^{nk}} = \begin{bmatrix} e^{-2\pi i 0\cdot0/N} & e^{-2\pi i 0\cdot1/N} & \cdots & e^{-2\pi i 0\cdot k/N}\\ e^{-2\pi i 1\cdot0/N} & e^{-2\pi i 1\cdot1/N} & \cdots & e^{-2\pi i 1\cdot k/N}\\ \vdots & \vdots & \ddots & \vdots\\ e^{-2\pi i n\cdot0/N} & e^{-2\pi i n\cdot1/N} & \cdots & e^{-2\pi i n\cdot k/N} \end{bmatrix}}
O cálculo dessa expressão leva em torno de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N^2} passos para o resultado. Uma amostra com 3,000 pontos precisa de 9,000,000 operações para a transformada ser obtida, tornando a DFT inviável para aplicações rápidas.
Transformada Rápida de Fourier
É possível calcular a transformada com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N \log_{2} N} passos. Para isso se dispõe de um algoritmo chamado Transformada Rápida de Fourier. Considera-se um conjunto de pontos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = 2^p} (com Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} inteiro, então, da definição da DFT
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_k =\sum_{n=0}^{N-1} f_n \cdot e^{-i \frac{2 \pi}{N}\cdot k\cdot n} }
podemos dividir o somatório em 2:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_k =\color{red}\sum_{n=0}^{N/2-1} f_{2n} \cdot e^{-i \frac{2 \pi}{N}\cdot k\cdot 2n} \color{black}+ \color{blue}\sum_{n=0}^{N/2-1} f_{2n+1} \cdot e^{-i \frac{2 \pi}{N}\cdot k\cdot (2n+1)} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \color{black}F_k =\color{red}\sum_{n=0}^{N/2-1} f_{2n} \cdot e^{-i \frac{2 \pi}{N/2}\cdot k\cdot n} \color{black}+ \color{blue}e^{-i\frac{2\pi}{N}k} \sum_{n=0}^{N/2-1} f_{2n+1} \cdot e^{-i \frac{2 \pi}{N/2}\cdot k\cdot n} }
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \color{black}F_k =\color{red}\sum_{n=0}^{N/2-1} f_{2n} \cdot e^{-i \frac{2 \pi}{N/2}\cdot k\cdot n} \color{black}+ \color{blue}~ C(k) ~ \sum_{n=0}^{N/2-1} f_{2n+1} \cdot e^{-i \frac{2 \pi}{N/2}\cdot k\cdot n} }
onde a soma em vermelho é a parte par e a soma em azul é a parte ímpar da transformada. As duas somas tem o mesmo expoente, que agora é dividido por Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N/2} . Desse expoente, é evidente a relação entre o ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} e o ponto Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k + N/2}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{-i \frac{2 \pi}{N/2}\cdot k\cdot n} = e^{-i \frac{2 \pi}{N/2}\cdot (k+N/2)\cdot n} = e^{-i \frac{2 \pi}{N/2}\cdot k\cdot n} \cdot e^{-i \frac{2 \pi}{N/2}\cdot N/2\cdot n} = e^{-i \frac{2 \pi}{N/2}\cdot k\cdot n} \cdot 1}
Com essa relação, podemos ver que Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_k} e Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{k+N/2}} tem o mesmo expoente e podem ser calculadas ao mesmo tempo. Mais que isso, a nova forma da transformada pode ser sucessivamente dividida, cada vez produzindo somas com limites menores.
Exemplo
Suponha que temos a função sinusoidal Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a(t) = sin(2\pi \cdot 1Hz \cdot t)} e fazemos quatro medidas no intervalo de 1 segundo, resultando em
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_0 = 0.00} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_1 = 1.00} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_2 = 0.00} Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_3 = -1.00}
Com essas 4 medidas, podemos dividir a soma 2 vezes:
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_k = \sum_{t=0}^3 a_t \cdot e^{-i \frac{2\pi}{4}\cdot k \cdot t}}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_k = \sum_{t_1=0}^1 a_{2t_1} \cdot e^{-i \frac{2\pi}{2}\cdot k \cdot t_1} + C_k^1\sum_{t_1=0}^1 a_{2t_1+1} \cdot e^{-i \frac{2\pi}{2}\cdot k \cdot t_1}}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_k = \sum_{t_2=0}^0 a_{4t_2} \cdot e^{-i \frac{2\pi}{1}\cdot k \cdot t_2} + C_k^2\sum_{t_2=0}^0 a_{4t_2+2} \cdot e^{-i \frac{2\pi}{1}\cdot k \cdot t_2} + C_k^1\sum_{t_2=0}^0 a_{4t_2+1} \cdot e^{-i \frac{2\pi}{1}\cdot k \cdot t_2} + C_k^3\sum_{t_2=0}^0 a_{4t_2+3} \cdot e^{-i \frac{2\pi}{1}\cdot k \cdot t_2}}
e como temos Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_k^j = (e^{-i\frac{2\pi}{N}k})^j} podemos calcular
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_0 = 1.00 \cdot C_0^1 - 1.00 \cdot C_0^3 = 0.00 + i0.00}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_1 = 1.00 \cdot C_1^1 - 1.00 \cdot C_1^3 = 0.00 - i2.00}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_2 = 1.00 \cdot C_2^1 - 1.00 \cdot C_2^3 = 0.00 + i0.00}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_3 = 1.00 \cdot C_3^1 - 1.00 \cdot C_3^3 = 0.00 + i2.00}
FFT para N diferente de uma potência de 2
Mesmo com a FFT sendo um algoritmo extremamente eficiente para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = 2^p} , esse dificilmente é o caso que encotramos. Ainda assim, para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} altamente composto (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = r_1\cdot r_2 \cdot ... \cdot r_m} ) o algoritmo ainda resulta em uma boa queda no tempo de cálculo.
Para o caso mais simples Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = r_1 \cdot r_2} a transformada pode ser escrita como
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(k_1,k_0) = \sum_{n_0=0}^{r_2-1}\left [ \sum_{n_1=0}^{r_1-1} x(n_1,n_0) e^{-i2\pi\cdot k \cdot n_1 \cdot r_2} \right ] e^{-i2\pi \cdot k \cdot n_0}}
onde
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k = k_1 \cdot r_1 + k_0 ~~~~~~~~ k_0 = 0,1,...,r_1-1 ~~~~~~~~ k_1 = 0,1,...,r_2-1}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = n_1 \cdot r_2 + n_0 ~~~~~~~~ n_0 = 0,1,...,r_2-1 ~~~~~~~~ n_1 = 0,1,...,r_1-1}
assim a transformada que antes necessitava de N cálculos, agora pode ser vista como Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_1 + r_2} cálculos.
Uma outra alternativa para o calculo da FFT é adicionar pontos 0 no fim da sequência. Por exemplo, para uma FFT de 5 pontos, basta adicionar 3 pontos 0 e calcular uma FFT pelos métodos já mostrados. Uma dificuldade dessa alternativa é que a transformada terá também 8 pontos, e apesar de corresponder ao mesmo formato da função original, está amostrada numa frequência diferente.
Algorítmo (usando recursão)
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle >>\mathbf{function} ~ FFT(N,\vec{a})}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle >>> ~~~~ \mathbf{if} ~ N = 1 ~ \mathbf{then}}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle >>> ~~~~~~~~ return ~ \vec{a};}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle >>> ~~~~ \mathbf{else}}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle >>>~~~~~~~~ E = FFT(N/2, (a_0, a_2, ..., a_{N-2}));}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle >>>~~~~~~~~ O = FFT(N/2, (a_1, a_3, ..., a_{N-1}));}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle >>>~~~~~~~~ \mathbf{for} ~ k = 0 ~ to ~ k <= N/2 -1 ~ \mathbf{do}}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle >>>~~~~~~~~~~~~ A_k=E_k+exp(-i2\pi k/N) * O_k;}
Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle >>>~~~~~~~~~~~~ A_{k+N/2}=E_k-exp(-i2\pi k/N) * O_k;}
Implementação
A natureza recursiva do algoritmo da transformada rápida de fourier o torna ideal para implementações em linguagens funcionais como Haskell. Abaixo exibimos as partes mais relevantes do código, onde omitimos inclusões de bibliotecas e a definição das funções auxiliares evens e odds.
--esse termo multiplica o somatório de termos ímpares
f xs n = exp $ -(0:+2*pi)*n / genericLength xs
--caso a função seja chamada com apenas dois termos, temos o caso base
ffti [x,y] n = x + y * (exp $ -(0:+pi)*n)
--caso contrário aplique a função recursivamente separando o somatório em
-- termos com índice par e com índice ímpar
ffti xs n = ffti (evens xs) n + f xs n * ffti (odds xs) n
--função que calcula os n coeficientes (ffti calcula um coeficiente)
fft xs [] = []
fft xs (y:ys) = (ffti xs y):(fft xs ys)
--exemplo
fft [0, 1, 4, 9] [0,1,2,3]
--saída ( :+ indica número complexo em Haskell)
[14.0 :+ 0.0, -4.0 :+ 8.0, -6.0 :+ 0.0, -4.0 :+ -8.0)]
Embora não seja uma linguagem puramente funcional Wolfram Mathematica também se presta a uma implementação direta e clara.
// caso base de uma lista contendo apenas dois termos
fft[{x_, y_}, n_] := x + y Exp[-I Pi n ]
// caso contrário, divida a lista entre termos com índice ímpar e par
// e aplique a função recursivamente
fft[f_List, n_] := fft[Downsample[f, 2, 1], n] +
Exp[-((I 2 Pi n )/Length[f])] fft[Downsample[f, 2, 2], n]
//acima calcula-se com um coeficiente abaixo calcula-se todos
fft[f_List] := Table[fft[f, n] // N, {n, 0, Length[f] - 1}]
//exemplo
fft[{0, 1, 4, 9}]
{14., -4. + 8. I, -6., -4. - 8. I}
Exemplos
Abaixo encontra-se alguns exemplos básicos da transformada de fourier com base no código acima porém com modificações para lidar com o caso em que o intervalo de amostragem é diferente de e cuja taxa de amostragem é qualquer (diferente de como assumido acima)
Gaussiana
A menos de uma normalização a função gaussiana é definida por: Aplicando a transformada de fourier na curva gaussiana obtem-se outra gaussiana.
Observa-se que uma curva larga no espaço real corresponde a uma curva estreita no espaço de fourier e vice-versa. Esse é um fato matemático amplamente conhecido e se exprime também na física pelo Princípio da Incerteza de Heisenberg. Abaixo uma curva gaussiana mais larga que a anterior e sua transformada correspondentemente mais estreita.
Uma função par em relação à origem possui uma expansão em fourier com termos ímpares nulos, no entanto, deslocando a gaussiana um pouco para a direita e, portanto, quebrando sua simetria, vemos que a sua transformada possui uma parte complexa:
Oscilador Harmônico Amortecido
A curva que representa um oscilador harmônico amortecido é descrita por onde o termo senoidal, periódico, é amortecido pelo termo exponencial que leva a oscilação rapidamente a zero.
A transformada de fourier dessa curva possui parte real e imaginária, da parte imaginária dessa curva é possível obter a frequência de ressonância do fenômeno representado por ela. No caso abaixo vemos que a frequência de ressonância vale
Abaixo a parte real da transformada:
Aplicações
Equação de Schrödinger: propagação de onda de probabilidade
O cálculo da evolução temporal da equação de schrödinger é computacionalmente exigente. A cada passo de tempo é necessário recalcular a posição da onda de probabilidade que representa a partícula em cada ponto do domínio. Portanto, torna-se vantajoso o uso da transformada de fourier rápida. Além disso a própria transformada faz parte da solução, pois também deseja-se obter a sua evolução temporal no espaço de momento. O código foi desenvolvido em python por Jake Vanderplas, no entanto, sob extensas modificações foi possível não apenas entender o código mas também modifica-lo para representar situações diferentes das propostas pelo autor. No site do autor encontra-se a explicação da teoria por trás do problema e também o funcionamento do algoritmo. A seguir exploramos a interação de uma onda de probabilidade com potenciais de diferentes formas.
A parte principal do código modificado é exibida abaixo. Nota-se que o autor utilizou o método Leapfrog para integrar as equações de movimento fazendo a seguinte sequência de operações: dar um meio passo no espaço real, tomar a transformada, dar um passo no espaço de momento, tomar a transformada inversa e finalmente dar um passo completo no espaço real.
def time_step():
global t, psi_mod_x, psi_mod_k, t_max
psi_mod_x *= x_evolve_half
for i in range(N_steps):
psi_mod_k = fft(psi_mod_x)
psi_mod_k *= k_evolve
psi_mod_x = ifft(psi_mod_k)
psi_mod_x *= x_evolve_half*x_evolve_half
psi_mod_k = fft(psi_mod_x)
t += dt * N_steps
t_max = t_max - 1
O restante do código ocupa-se somente de inicialização de valores, definição do potencial e escrita dos resultados.
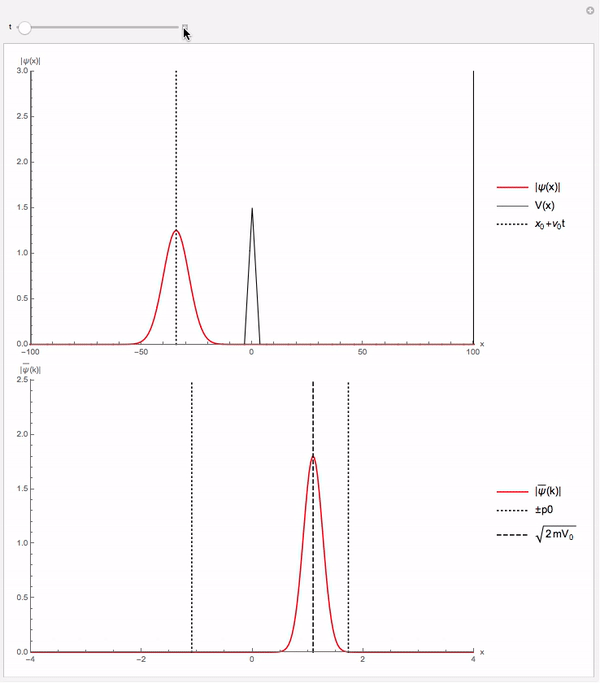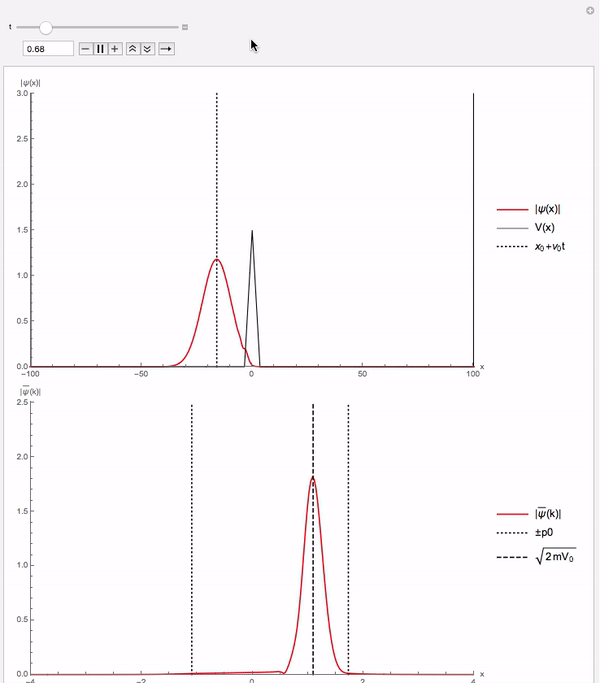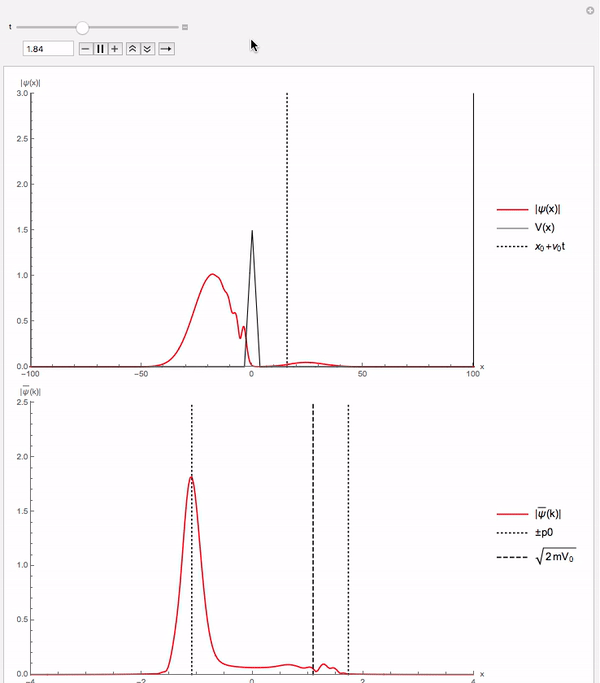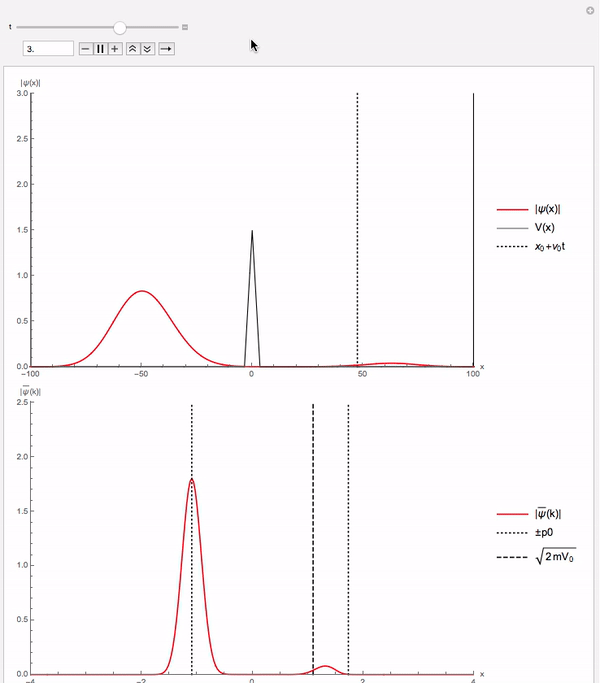
Potencial Quadrado
O potencial quadrado foi o exemplo escolhido pelo autor do código. Nesse exemplo fica visível que uma porção da onda de probabilidade atravessa o potencial embora classicamente não tenha energia suficiente para tal feito. Essa é uma demonstração numérica do efeito de tunelamento.
Potencial Triangular
O potencial triangular, por ter uma base mais larga, coíbe o efeito de tunelamento, no entanto, uma pequena porção da onda incidente ainda consegue transpor a barreira.
Potencial Batman
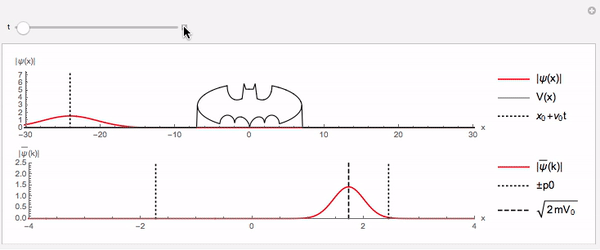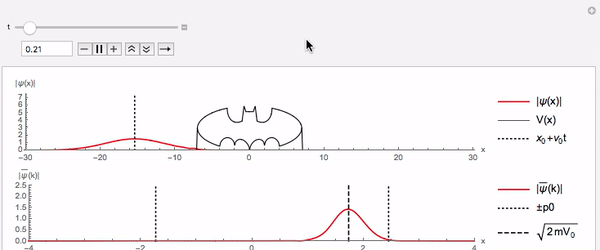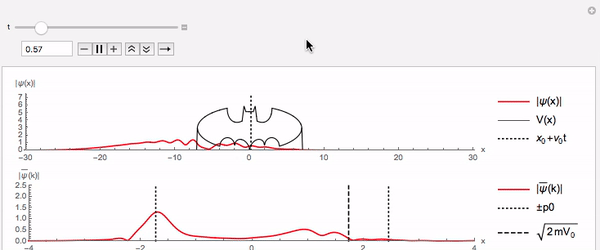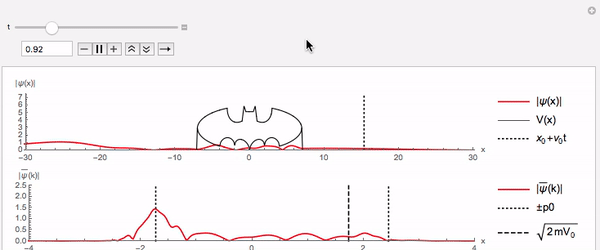
Em cursos básicos de quântica normalmente resolve-se apenas o potencial quadrado, às vezes, excepcionalmente, apresenta-se o potencial triangular. Isso se deve a dificuldade em tratar casos de potenciais irregulares analiticamente. Mas em casos reais os potenciais são extremamente irregulares. A solução numérica trata tais casos com naturalidade e sem qualquer alteração. Em particular, um potencial tipo batman é encarado sem problemas:
A parte superior da curva é apenas ilustrativa (pois não faz sentido matemático nem físico)
Padrões de Difração
A transformada rápida é muito utilizada no tratamento de imagens. Software como ImageJ ou Matlab possuem muitas ferramentas que fazem uso da técnica. Uma aplicação específica da FFT é na análise de imagens de partículas nanométricas obtidas por um microscópio eletrônico de transmissão. Esse equipamento produz um interferograma que (a menos de correções) representa a imagem real do que se está observando mas também produz uma segunda imagem, localizada no ponto focal da lente, que é o padrão de difração da imagem real. Essa imagem é uma visualização do espaço recíproco, ou seja, da transformada do espaço real.
Abaixo está uma imagem de um plano de átomos de ouro obtida por um microscópio de transmissão eletrônica com uma escala de 2 nanômetros na qual destacamos uma região (quadrado vermelho) na qual tomaremos a transformada de fourier. A imagem em si é representada por uma matrix 800x800 onde cada elemento da matrix é um valor de intensidade sendo 0 para totalmente escuro e 255 para totalmente claro.
Utilizando, por exemplo o software Matlab podemos tomar a transformada inversa dessa imagem. A transformada de fourier produz o padrão de difração que revela a periodicidade da imagem. O código em Matlab é bem simples:
function imagefft(I)
F = fft2(I);
F = fftshift(F); % centraliza a FFT
F = abs(F); % obtem a magnitude (desnecessário, nossa imagem varia de 0 a 255)
F = log(F+1); % escala logaritmica, +1 por que log(0) é indefinido
F = mat2gray(F); % renormaliza a imagem de 0-255 para 0-1
imshow(F,[]) % exibe o resultado
end
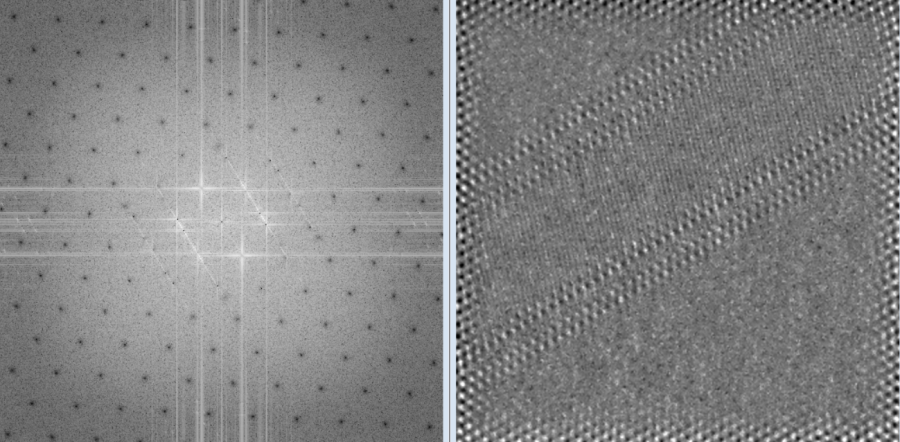
Cada par de pontos simétricos em relação ao ponto central representa um conjunto de planos paralelos no espaço real, sendo a imagem real o conjunto de todos os planos representados por todos os pontos somado ao ruído da imagem. Observe que a imagem original, além de ruído, apresenta três planos diferentes como pode-se notar pela orientação dos átomos. Isso explica a presença de linhas claras ao redor dos pontos de difração. Um cristal perfeito, por outro lado, possuiria um padrão de difração de pontos localizados e não discos com linhas como vemos num cristal real.
A seguir vejamos como decompor essas informações. Aplicando uma máscara sobre a imagem podemos selecionar apenas um par de pontos e ver a qual conjunto de planos do espaço real ele está relacionado:
Para descobrir qual é o conjunto de planos tomamos a transformada inversa:
Como mencionado se selecionarmos todos os pontos e tomarmos a transformada inversa obteremos a imagem original, no entanto, removendo boa parte dos ruídos - a parte que deixamos de fora da máscara.
Se quisermos ver a composição do ruído podemos tomar a máscara inversa e aplicar a transformada inversa, obtendo:
Referências Bibliográficas
[2] Kreyszig, Erwin. Advanced Engineering Mathematics. Wiley, 2011.
[3] Scherer, Claudio. Métodos Computacionais da Física.
[4] Richard; Faires, Douglas. Numerical Analysis, 2011

![{\displaystyle [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/348d40bf3f8b7e1c00c4346440d7e2e4f0cc9b91)