Motility-Induced Phase Separation(MIPS): mudanças entre as edições
| (74 revisões intermediárias pelo mesmo usuário não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
'''Grupo: Bernardo Boatini e Murilo Kessler Azambuja''' | '''Grupo: Bernardo Boatini e Murilo Kessler Azambuja''' | ||
Neste trabalho iremos seguir de perto o artigo "''Critical motility-induced phase separation belongs to the Ising universality class''" <ref name = BENJAMIN> </ref> de Benjamin Partridge e Chiu Fan Lee. | |||
==Introdução== | ==Introdução== | ||
A matéria ativa é um tipo de sistema fora do equilíbrio termodinâmico, onde cada "partícula" ou "agente" do sistema tem a capacidade dissipar energia na forma de forças mecânicas exercidas sobre o ambiente no qual está imerso. Esses sistemas muitas vezes podem exibir vários fenômenos novos, como movimentos coletivos quando exige-se um alinhamento das partículas ( | A matéria ativa é um tipo de sistema fora do equilíbrio termodinâmico, onde cada "partícula" ou "agente" do sistema tem a capacidade dissipar energia na forma de forças mecânicas exercidas sobre o ambiente no qual está imerso. Esses sistemas muitas vezes podem exibir vários fenômenos novos, como movimentos coletivos quando exige-se um alinhamento das partículas (como bio-polímeros que se auto organizam, tipo os microtúbulos que são parte do citoesqueleto celular, ou cardumes de peixe, por exemplo), ou os chamados MIPS (Motility-Induced Phase Separation) que são sistemas que apresentam uma mudança de fase física devido à interações entre partículas que proíbem a ocupação simultânea de um volume do espaço além delas apresentarem persistência em uma certa direção de movimento. Nestes sistemas, os agentes possuem a capacidede de auto-propulsão, de forma que a condição de balanço detalhado é quebrada no nível microscópico <ref name = BENJAMIN></ref>, uma vez que as partículas possuem uma direção preferencial de movimento.Estes tipos de sistema muitas vezes podem ser tratados a partir de uma abordagem hidrodinâmica, na qual são chamados de fluidos ativos, e divergem do comportamento usual de fluidos compostos de matéria | ||
usual inativa, os quais são descritos pela equação de Navier-Stokes. | usual inativa, os quais são descritos pela equação de Navier-Stokes. | ||
Apesar desses sistemas fundamentalmente quebrarem a condição do balanço detalhado, ainda não é claro se o comportamento estatístico universal de sistemas de fluidos ativos necessariamente divergem daqueles | Apesar desses sistemas fundamentalmente quebrarem a condição do balanço detalhado, ainda não é claro se o comportamento estatístico universal de sistemas de fluidos ativos necessariamente divergem daqueles de sistemas em equilíbrio. A investigação de comportamentos universais nestes tipos de sistema, além de ser um interece central na física, também pode nos permitir utilizar conhecimentos já bem estabelecidos (como a transição de fase em sistemas de matéria em equilíbrio termodinâmico) para descrever sistemas novos. Neste trabalho foi reproduzido o artigo <ref name=BENJAMIN> https://arxiv.org/pdf/1810.06112.pdf Benjamin Partridge, Chiu Fan Lee, "CRITICAL MOTILITY-INDUCED PHASE SEPARATION BELONGS TO THE ISING UNIVERSALITY CLASS" </ref> onde foi investigada o comportamento crítico de um sistema com MIPS e se viu que este tipo de sistema pertence à classe de universalidade de sistemas em equilíbrio como o modelo de Ising para spin. Para tal, foi utilizada três abordagens diferentes: um modelo hidrodinâmico, uma descrição baseada em teoria de campos e a simulação de um modelo de rede hexagonal. | ||
==Modelo== | ==Modelo== | ||
| Linha 13: | Linha 15: | ||
[[Arquivo: foto.png|thumb|upright=2|center|none|alt=Alt text|FIGURA 1: Imagem retirada de <ref NAME = BENJAMIN></ref>. Em (a) vemos a difusão devido à rotação da direção de movimento preferencial da partícula, em (b) temos o "movimento balístico" (seta verde) e a difusão devido à translação da partícula (setas azuis) e, em (c), vemos a interação entre partículas em sítios vizinhos, impedindo a ocupação simultânea do mesmo sítio por duas partículas.]] | [[Arquivo: foto.png|thumb|upright=2|center|none|alt=Alt text|FIGURA 1: Imagem retirada de <ref NAME = BENJAMIN></ref>. Em (a) vemos a difusão devido à rotação da direção de movimento preferencial da partícula, em (b) temos o "movimento balístico" (seta verde) e a difusão devido à translação da partícula (setas azuis) e, em (c), vemos a interação entre partículas em sítios vizinhos, impedindo a ocupação simultânea do mesmo sítio por duas partículas.]] | ||
Uma forma de modelar este sistema é considerá-lo um fluido ativo polar e compressível sem interações de alinhamento entre partículas, de forma que não se espera observar movimentos coletivos. Tal sistema é descrito de forma contínua pela chamada equação de Toner-Tu. | Uma forma de modelar este sistema é considerá-lo um fluido ativo polar e compressível sem interações de alinhamento entre partículas, de forma que não se espera observar movimentos coletivos. Tal sistema é descrito de forma contínua pela chamada equação de Toner-Tu <ref name = BENJAMIN> </ref>. | ||
De um ponto de vista microscópico, podemos usar uma formulação discreta baseada na teoria de campos. Neste caso, consideramos uma rede hexagonal bidimensional, com o numero de ocupação de cada sítio da rede restringido por uma constante <math>M</math> (futuramente diremos que <math>M =1</math>, de forma que apenas uma partícula pode ocupar cada sítio). | De um ponto de vista microscópico, podemos usar uma formulação discreta baseada na teoria de campos. Neste caso, consideramos uma rede hexagonal bidimensional, com o numero de ocupação de cada sítio da rede restringido por uma constante <math>M</math> (futuramente diremos que <math>M =1</math>, de forma que apenas uma partícula pode ocupar cada sítio). | ||
| Linha 19: | Linha 21: | ||
===Modelo no Continuo=== | ===Modelo no Continuo=== | ||
As equações de Tuner-Tu são dadas por <ref NAME = BENJAMIN></ref> | As equações de Tuner-Tu para o modelo em questão são dadas por <ref NAME = BENJAMIN></ref> | ||
<center><math> \partial_t \rho + \nabla \cdot \mathbf{g} = 0, \qquad (1a) </math> | <center><math> \partial_t \rho + \nabla \cdot \mathbf{g} = 0, \qquad (1a) </math> | ||
<math> \partial_t \mathbf{g} = -\zeta \nabla\rho - \kappa \mathbf{g} + \mu \nabla^2\mathbf{g} + \mathbf{f} | <math> \partial_t \mathbf{g} = -\zeta \nabla\rho - \kappa \mathbf{g} + \mu \nabla^2\mathbf{g} + \mathbf{f}, \qquad (1b) </math> | ||
</center> | </center> | ||
onde <math> \rho </math> é o campo de densidade de massa e <math> \mathbf{g} </math> é o campo de densidade de momentum. A equação (1a) diz respeito à conservação de massa do sistema como um todo. A equação (1b) se assemelha muito à equação de Navier-Stokes, assim podemos ver que o primeiro termo da equação caracteriza a compressibilidade do fluido, o segundo termo representa uma difusão do campo de momentum (o sinal negativo indica que o campo de momentum diminui com o passar do tempo), o terceiro termo representa a viscosidade do fluido e <math> \mathbf{f} </math> é um ruído Gaussiano com estatísticas espaço-temporais dadas por | |||
<center> | <center> | ||
<math> \langle \mathbf{f}(t, \mathbf{r}) \rangle = 0,\ \langle\mathbf{f}(t, \mathbf{r})\mathbf{f}(t', \mathbf{r'})\rangle = 2D \delta(t-t')\delta(\mathbf{r}-\mathbf{r'}),</math> | <math> \langle \mathbf{f}(t, \mathbf{r}) \rangle = 0,\ \langle\mathbf{f}(t, \mathbf{r})\mathbf{f}(t', \mathbf{r'})\rangle = 2D \delta(t-t')\delta(\mathbf{r}-\mathbf{r'}),</math> | ||
</center> | </center> | ||
onde <math> D </math> é a intensidade do ruído. | onde <math> D </math> é a intensidade do ruído. | ||
= | No mesmo artigo <ref name = BENJAMIN></ref> os autores argumentam que, devido à ausência de interações de alinhamento entre partículas, a emergência de movimento coletivo é impossível. Por este motivo, temos que o campo de densidade de momentum deve ir à zero no limite hidrodinâmico, de forma que <math> \mathbf{g} </math> não é uma variável livre e pode ser escrita em função de <math> \rho </math>. Desta forma, <ref name = BENJAMIN> </ref> obtêm que | ||
<center> | |||
<math> | |||
\mathbf{g} = -\nabla \Big [(a_1\phi+a_2\phi^2+a_3\phi^3) - (\nabla^2(b\phi)) \Big ] + \mathbf{f}, | |||
</math> | |||
</center> | |||
Como já foi dito antes, no modelo discreto é utilizado uma rede bidimensional hexagonal com número de ocupação máximo <math> M </math> para cada sítio da rede. Os agentes são divididos em seis tipos distintos de partículas ativas, cada uma se move em uma direção <math> \theta_i </math> (as diagonais do hexágono) e somente vai saltar para o sítio adjacente ao longo desta direção, com uma taxa que depende da ocupação do sítio em questão. Além disso, é possível que uma partícula se transforme em outra, com uma taxa <math> \sigma </math>, correspondendo assim a um ruído rotacional de cada partícula. Utilizando a notação utilizada em <ref NAME = BENJAMIN> </ref>, temos que a rede hexagonal é caracterizado pelo conjunto de vetores <math> \mathbf{R} </math> e a orientação ou tipo da partícula ativa pelo índice <math> i </math>. Desta forma o número de partículas do tipo <math> i </math> ocupando o sítio <math> \mathbf{R} </math> da rede é denotado por <math> A^{\theta_i}_{\mathbf{R}} </math>. Com o formalismo desenvolvido em <ref name=ALEXANDRE> Disponível em: https://arxiv.org/pdf/0709.1325.pdf Alexandre Lefèvre, Giulio Biroli, "DYNAMICS OF INTERACTING PARTICLE SYSTEMS: STOCHASTIC PROCESS AND FIELD THEORY" </ref>, temos que a teoria de campos nos fornece | de modo que, ao substituir em (1a), temos | ||
<center> | |||
<math> | |||
\partial_t \phi = \nabla^2 \frac{\delta H}{\delta \phi} + \nabla \cdot \mathbf{f}, \qquad (2) | |||
</math> | |||
</center> | |||
onde <math> \phi(\mathbf{r})=\rho (\mathbf{r}) - \rho_0 </math> para alguma constante <math> \rho_0 </math> e <math> H = \frac{a_1}{2}\phi^2 + \frac{a_2}{3}\phi^3 + \frac{a_3}{4}\phi^4 + \frac{b}{2}\big( \nabla \phi \big)^2</math> é o Hamiltoniano de Ginzburg-Landau. A partir da equação (2), vemos que é possível descrever o sistema a partir da manipulação de dois parâmetros principais: o campo de densidade de partículas <math> \rho </math> (ou <math> \phi </math>, a menos de uma constante) e a intensidade <math> D </math> do ruído <math> \mathbf{f} </math>. | |||
===Modelo no Espaço Discreto=== | |||
Como já foi dito antes, no modelo discreto é utilizado uma rede bidimensional hexagonal com número de ocupação máximo <math> M </math> para cada sítio da rede. Os agentes são divididos em seis tipos distintos de partículas ativas, cada uma se move em uma direção <math> \theta_i </math> (as diagonais do hexágono) e somente vai saltar para o sítio adjacente ao longo desta direção, com uma taxa que depende da ocupação do sítio em questão. Além disso, é possível que uma partícula se transforme em outra, com uma taxa <math> \sigma </math>, correspondendo assim a um ruído rotacional de cada partícula. Utilizando a notação utilizada em <ref NAME = BENJAMIN> </ref>, temos que a rede hexagonal é caracterizado pelo conjunto de vetores <math> \mathbf{R} </math> e a orientação ou tipo da partícula ativa pelo índice <math> i </math>. Desta forma o número de partículas do tipo <math> i </math> ocupando o sítio <math> \mathbf{R} </math> da rede é denotado por <math> A^{\theta_i}_{\mathbf{R}} </math>. Com o formalismo desenvolvido em <ref name=ALEXANDRE> Disponível em: https://arxiv.org/pdf/0709.1325.pdf Alexandre Lefèvre, Giulio Biroli, "DYNAMICS OF INTERACTING PARTICLE SYSTEMS: STOCHASTIC PROCESS AND FIELD THEORY" </ref>, temos que a teoria de campos nos fornece uma ação dada por | |||
<center> | <center> | ||
<math> | <math> | ||
S = \int dt \sum_{\mathbf{R}} \Bigg \{ \sum_i \Bigg [ \hat{A}^{\theta_i}_{\mathbf{R}} \partial_t A^{\theta_i}_{\mathbf{R}} | S = \int dt \sum_{\mathbf{R}} \Bigg \{ \sum_i \Bigg [ \hat{A}^{\theta_i}_{\mathbf{R}} \partial_t A^{\theta_i}_{\mathbf{R}} | ||
</math> | </math> | ||
<math> | <math> | ||
-\gamma\Big (M-N_{\mathbf{R}+\mathbf{e}_{\theta_i}} \Big ) A^{\theta_i}_{\mathbf{R}} \Big ( e^{ \hat{A}^{\theta_i}_{\mathbf{R}+\mathbf{e}_{\theta_i}} - \hat{A}^{\theta_i}_{\mathbf{R}}} - 1 \Big ) \Bigg ] \qquad ( | -\gamma\Big (M-N_{\mathbf{R}+\mathbf{e}_{\theta_i}} \Big ) A^{\theta_i}_{\mathbf{R}} \Big ( e^{ \hat{A}^{\theta_i}_{\mathbf{R}+\mathbf{e}_{\theta_i}} - \hat{A}^{\theta_i}_{\mathbf{R}}} - 1 \Big ) \Bigg ] \qquad (3) | ||
</math> | </math> | ||
<math> | <math> | ||
-\sum_{\langle i,j \rangle} \sigma A^{\theta_i}_{\mathbf{R}} \Big (e^{\hat{A}^{\theta_j}_{\mathbf{R}-\hat{A}{\theta_i}_{\mathbf{R | -\sum_{\langle i,j \rangle} \sigma A^{\theta_i}_{\mathbf{R}} \Big (e^{\hat{A}^{\theta_j}_{\mathbf{R}} - \hat{A}^{\theta_i}_{\mathbf{R}}}-1 \Big ) \Bigg \}, | ||
</math> | </math> | ||
</center> | </center> | ||
onde <math> N_\mathbf{R} = \sum_j A_{\mathbf{R}}^{\theta_j}</math> é o número de partículas total ocupando o sítio <math> \mathbf{R} </math>. A segunda linha da equação (3) diz respeito ao termo de transição entre uma posição <math> \mathbf{R} </math> e uma posição <math> \mathbf{R}+\mathbf{e}_{\theta_i} </math> na rede hexagonal. Esta transição ocorre à uma taxa <math> \gamma \Big (M-N_{\mathbf{R} + \mathbf{e}_{\theta_i}} \Big ) </math>, de forma que a taxa de transição para o sítio decresce com o aumento do número de partículas ocupando o mesmo. Se o número de partículas ocupando o sítio é <math> M </math>, então a taxa de transição é nula, indicando que não será possível que ocorra uma transição para este sítio. Este termo modela as interações de exclusão de volume discutidas anteriormente. Em nosso caso específico tomaremos <math> M=1 </math>. Além disso, na terceira linha da equação (3) corresponde à transição de tipo da partícula, i.e., à transição do movimento preferencial da partícula de uma orientação <math> \theta_i </math> para uma <math> \theta_j </math>. Esta transição ocorre com uma taxa <math> \sigma </math> e a notação <math> \langle i,j \rangle </math> indica que a partícula somente trocará para uma orientação <math> \theta_j</math> que seja adjascente à orientação <math> \theta_i </math> inicial. | |||
==Implementação== | ==Implementação== | ||
| Linha 71: | Linha 94: | ||
Em modelos do tipo LGCA(Lattice Gas Celular Automata) o tipo de rede, bem como as topologias usadas, podem ser determinantes para as medidas e caracterizações do estado macroscópico. A simetria hexagonal se mostra uma boa alternativa para aumentar os graus de liberdade de uma partícula numa rede, quando comparada com a simetria quadrada. Na geometria hexagonal, assim como na quadrada, todos os sítios vizinhos possuem uma mesma distancia entre si só que com 6 graus de liberdade ao invés de quatro. | Em modelos do tipo LGCA(Lattice Gas Celular Automata) o tipo de rede, bem como as topologias usadas, podem ser determinantes para as medidas e caracterizações do estado macroscópico. A simetria hexagonal se mostra uma boa alternativa para aumentar os graus de liberdade de uma partícula numa rede, quando comparada com a simetria quadrada. Na geometria hexagonal, assim como na quadrada, todos os sítios vizinhos possuem uma mesma distancia entre si só que com 6 graus de liberdade ao invés de quatro. | ||
[[Arquivo: Hex_grid.png|thumb|upright= | [[Arquivo: Hex_grid.png|thumb|upright=3|center|none|alt=Alt text|FIGURA 2: Imagem adaptada de <ref NAME = CELULAR></ref>. As setas duplas em verde sinalizam os sentidos que seguem trajetórias fechadas passando por só uma borda na topologia "armchair"(a) e "zigzag" (b)]] | ||
Existem duas topologias possíveis em uma rede hexagonal: "zigzag" e "armchair"<ref NAME = CELULAR> HATZIKIROU, Haralambos et al. Extracting cellular automaton rules from physical Langevin equation models for single and collective cell migration. Journal of Mathematical Biology, [s. l.], 2017. </ref>, e a diferença das duas está principalmente na implementação das condições de contorno periódicas. No caso da topologia em "zigzag"( | Existem duas topologias possíveis em uma rede hexagonal: "zigzag" e "armchair"<ref NAME = CELULAR> HATZIKIROU, Haralambos et al. Extracting cellular automaton rules from physical Langevin equation models for single and collective cell migration. Journal of Mathematical Biology, [s. l.], 2017. </ref>, e a diferença das duas está principalmente na implementação das condições de contorno periódicas. No caso da topologia em "zigzag"(FIG.2b), o espaço é representado em um paralelogramo, e existem 4 sentidos em que cruzando uma parede a partícula fecha sua trajetória sem ter que cruzar nova mente outra parede do sistema. Na topologia "armchair"(FIG.2a) por outro lado só existem 2 sentidos em que isso acontece. | ||
===Sub-Box Sampling Method=== | ===Sub-Box Sampling Method=== | ||
O método das subcaixas consiste em dividir o sistema em uma certa quantidade de subsistemas de interesse, permitindo observar | O método das subcaixas consiste em dividir o sistema em uma certa quantidade de subsistemas de interesse, permitindo observar as flutuações de densidades, para um valor fixo de partículas no sistema, apenas nessas regiões. | ||
Nesse trabalho o sistema foi dividido em 4 caixas de tamanho <math>L \times L</math>: 2 centradas no centro de massa horizontal do sistema e duas centradas na região horizontal "mais rarefeita", que consequentemente esta a uma distancia de <math> 3L</math> do centro de massa. | Nesse trabalho o sistema foi dividido em 4 caixas de tamanho <math>L \times L</math>: 2 centradas no centro de massa horizontal do sistema e duas centradas na região horizontal "mais rarefeita", que consequentemente esta a uma distancia de <math> 3L</math> do centro de massa. | ||
| Linha 82: | Linha 105: | ||
Quando os parâmetros permitem que haja separação de fase, duas subcaixas ficam posicionadas exatamente sobre o centro da fase liquida e a mesma coisa para a fase gasosa, permitindo uma medição mais precisa das flutuações de densidade sem considerar as regiões de fronteira. | Quando os parâmetros permitem que haja separação de fase, duas subcaixas ficam posicionadas exatamente sobre o centro da fase liquida e a mesma coisa para a fase gasosa, permitindo uma medição mais precisa das flutuações de densidade sem considerar as regiões de fronteira. | ||
Porém, essas flutuações se tornam especialmente relevantes no ponto crítico, onde o uso de subcaixas se torna | Porém, essas flutuações se tornam especialmente relevantes no ponto crítico, onde o uso de subcaixas se torna muito importante na extração medidas para classificar a transição de fase do modelo em análise. | ||
===Medida 1=== | ===Medida 1=== | ||
A primeira medida utilizada para comparar o MIPS com o Ising foi a compressibilidade isotérmica dos subsistemas <math> \chi_L </math> definida da seguinte forma | |||
<math> \chi_L = \frac{\langle N^{2} \rangle_L - \langle N \rangle_L^2}{\langle N \rangle_L}</math> | |||
onde <math> \langle N \rangle_L </math> denota a média do número de partículas contidas em um subsistema de tamanho L. | |||
A compressibilidade isotérmica possui um fator de escala com o tamanho do sistema(<math> \chi_L \alpha L^{\gamma / \nu} </math>), que é conhecido para o caso do Ising 2D (<math> \gamma / \nu = 7/4 </math>). | |||
===Medida 2=== | ===Medida 2=== | ||
A segunda medida proposta é a derivada do cumulante de quarta ordem (<math> U_{4} </math>) com relação a distância adimensional do ponto crítico (<math> \tau = \frac{\sigma - \sigma_{c}}{\sigma} </math>) calculada no ponto crítico(<math> \tau = 0 </math>). O cumulante é definido da seguinte forma | |||
<math> U_{4} = \frac{\langle \Delta \rho^2 \rangle_L^2}{\langle \Delta \rho^4 \rangle_L} </math> | |||
<math> \Delta \rho = \rho - \langle \rho \rangle_L </math> | |||
Em <ref NAME = BENJAMIN></ref> <math> \langle . \rangle_L </math> é descrito como: "''[...] an average over the four sub-boxes of finite size L [...]''" | |||
O cumulante de quarta ordem possui a propriedade de ser invariante frente a escala do sistema no ponto crítico(FIG.3), e por isso a sua derivada no ponto critico se torna um fator de escala importante para comparar o estado macroscópico do MIPS e do Ising. | |||
[[Arquivo: Cumulante.png|thumb|upright=2|center|none|alt=Alt text|FIGURA 3: Imagem retirada de <ref NAME = BENJAMIN></ref>. Mostra o comportamento esperado do cumulante de quarta ordem para o modelo de MIPS nas proximidades da criticidade em sistemas de diferentes tamanhos.]] | |||
Em <math> \tau = 0 </math> a derivada do cumulante de quarta ordem, com respeito a <math> \tau </math>, possui um fator de escala <math> \alpha L^{1/ \nu} </math>, que também pode ser encontrado no modelo de Ising(<math> \nu = 1 </math>). | |||
==Resultados== | ==Resultados== | ||
Com base nos Diagrama de Fase do sistema(FIG.4) foi possivel extrair os parâmetros característicos dos principais comportamentos do sistema, e testar a simulação nesses diferentes casos. O tempo de relaxação do sistema <math> t_{relax} = 5\times10^5 MCS </math>(medido a partir do tem pode correlação) foi o mesmo utilizado no artigo. a densidade do sistema foi fixada em <math>\rho = 0.522</math> em todos as simulações. Embora o artigo <ref NAME = BENJAMIN></ref> não especifique a topologia de rede utilizada, nesta análise foi adotada a topologia "armchair". | |||
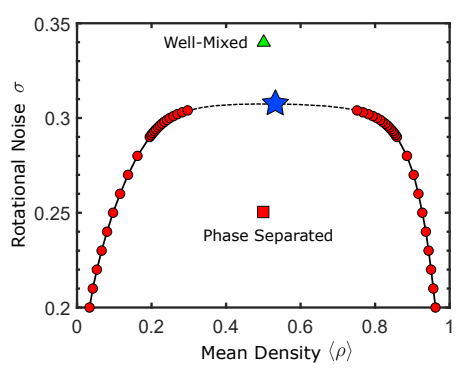
[[Arquivo: Diagrama_MIPS.png|thumb|upright=2.5|center|none|alt=Alt text|FIGURA 4: Imagem retirada de <ref NAME = BENJAMIN></ref>. Mostra o diagrama de fase do sistema.]] | |||
No estado de equilíbrio, após o <math>t_{relax}</math>, para <math>\sigma = 0.34</math> tem-se um comportamento visualmente mais homogêneo(FIG.5), onde o ruído é tão intenso que nenhuma fase é formada no sistema. | |||
[[Arquivo: Well_Mixed.png|thumb|upright=3|center|none|alt=Alt text|FIGURA 5:Imagem de simulação por Bernardo Boatini. Sistema Homogêneo no estado estacionário. L=36]] | |||
Quando <math>\sigma = 0.25</math> é possível simular um estado estacionário, após <math>t_{relax}</math>, em que ocorre separação de fase. Na figura 6 é evidente a distinção entre fase densa e fase rarefeita. | |||
[[Arquivo: Phase_Separated.png|thumb|upright=3|center|none|alt=Alt text|FIGURA 6:Imagem de simulação por Bernardo Boatini. Sistema em separação de fase no estado estacionário. L=36]] | |||
Nesses dois casos nenhum dado de ocupação(e consequentemente densidade) das subcaixas foi extraído. | |||
Por fim, temos uma imagem do sistema(FIG.7) em ponto crítico <math>\sigma = 0.305</math>, onde qualitativamente constata-se que a fase densa e a fase rarefeita não são distinguíveis no sistema e ambas não encontram uma região de estabilidade ao longo da simulação. Além disso, as flutuações de densidade nas subcaixas, que podem ser medidas através do numero de partículas em cada subcaixa(TABELAS 1 e 2) dividido pela área de cada uma, são, em princípio, diferentes, e isso que permite as análises do fator de escala que virão a seguir. | |||
[[Arquivo: Tabela2.png|thumb|upright=2.8|right|none|alt=Alt text|TABELA 2: Número de partículas(ocupação) em cada uma das subcaixas do sistema em 10 estados de equilíbrios diferentes para L=30 e L=36]] | |||
[[Arquivo: Tabela1.png|thumb|upright=2.8|left|none|alt=Alt text|TABELA 1: Número de partículas(ocupação) em cada uma das subcaixas do sistema em 10 estados de equilíbrios diferentes para L=18 e L=24]] | |||
[[Arquivo: Critical_Point.png|thumb|upright=3|center|none|alt=Alt text|FIGURA 7:Imagem de simulação por Bernardo Boatini. Sistema para <math>\sigma</math> crítico no estado estacionário. L=36]] | |||
Para realizar a comparação dos fatores de escala 10 amostras independentes(amostradas a cada <math>t_{relax}</math>) foram medidas em 4 tamanhos de rede diferentes L = {18, 24, 30, 36}, em cada uma das 10 amostras, 4 subcaixas mediram o número de partículas em diferentes estados estacionários(TABELAS 1 e 2). A análise de dados com respeito a Medida 1 são apresentados na FIGURA 8. | |||
[[Arquivo: Incompressibilidade.png|thumb|upright=3|center|none|alt=Alt text|FIGURA 8: Compressibilidade Isotérmica(<math>\Chi_L</math>) como função de L no sistema de partículas ativas(azul) e para o Ising 2D(laranja)<ref NAME = BENJAMIN></ref>. Gráfico em escala log-linear com barras de erro iguais ao maior erro padrão extraído dentre os 4 pontos.]] | |||
É possível ver, que com uma precisão de <math>R^2 = 0.9805</math> a tendência de escala do <math>\Chi_L</math> do sistema de partículas ativas(aproximadamente <math>\alpha L^{1.4714}</math>) é similar a lei de potência do <math>\Chi_L</math> no Ising 2D. | |||
Os dados nas proximidades do ponto crítico foram extraídos, mas os valores de <math>U_4</math> resultantes não foram satisfatórios. Aparentemente a definição de <math>\langle . \rangle_L</math> é diferente para as 2 medidas propostas, e por esse motivo a analise de dados foi prejudicada; ou seria necessário uma amostragem com mais de 10 amostra para desprezar o ruído nas medidas, já que em <ref NAME = BENJAMIN></ref> o numero de estados estacionários utilizados na estatística é da ordem de <math>10^3</math>. | |||
==Código== | |||
<source lang="c"> | |||
#include <stdio.h> | |||
#include <stdlib.h> | |||
#include <time.h> | |||
#include <math.h> | |||
#include "mc.h" | |||
#define L 30 //L = 18, 24, 30, 36 no papper | |||
#define h 2 //h = 2 no papper | |||
#define c 6 //c = 6 no papper | |||
#define S 10800 //S = (h*L)*(c*L) | |||
#define N 5638 //rho = N/S = 0.522 no papper | |||
int ngb[S][6]; | |||
int sb[h*2][L*L]; | |||
void sb_creator(void) { | |||
int i, j, n, aux; | |||
//cria subcaixas | |||
for(n=0; n<h*2; n++){ | |||
j = 0; | |||
aux = n*c*L*L + (c*L/2 - L/2 + j*c*L); | |||
if(n<h){ | |||
for(i=0; i<L*L; i++){ | |||
if(i == (j+1)*L){ | |||
j = j+1; | |||
} | |||
aux = n*c*L*L + (c*L/2 - L/2 + j*c*L); | |||
sb[n][i] = aux + i - j*L; | |||
} | |||
} | |||
else{ | |||
aux = h*2 - (n+1); | |||
for(i=0; i<L*L; i++){ | |||
if(i == (j+1)*L){ | |||
j = j+1; | |||
} | |||
if(i-j*L < L/2){ | |||
sb[n][i] = sb[aux][i] + c*L/2; | |||
} | |||
if(i-j*L >= L/2){ | |||
sb[n][i] = sb[aux][i] - c*L/2; | |||
} | |||
} | |||
} | |||
} | |||
} | |||
void ngb_creator(void) { | |||
int i, j, n; | |||
//cria matriz de vizinhos | |||
ngb[0][0]= S - c*L + 1; //superior direita | |||
ngb[0][1]= 1; //direita | |||
ngb[0][2]= c*L + 1; //inferior direita | |||
ngb[0][3]= c*L; //inferior esquerda | |||
ngb[0][4]= c*L - 1; //esquerda | |||
ngb[0][5]= S - c*L; //superior esquerda | |||
for(i=1;i<c*L-1;i++){ | |||
ngb[i][0]= i + S - c*L + 1; | |||
ngb[i][1]= i + 1; | |||
ngb[i][2]= i + c*L + 1; | |||
ngb[i][3]= i + c*L; | |||
ngb[i][4]= i - 1; | |||
ngb[i][5]= i + S - c*L; | |||
} | |||
ngb[c*L-1][0]= S - c*L; | |||
ngb[c*L-1][1]= 0; | |||
ngb[c*L-1][2]= c*L; | |||
ngb[c*L-1][3]= 2*c*L - 1; | |||
ngb[c*L-1][4]= c*L - 2; | |||
ngb[c*L-1][5]= S - 1; | |||
j = 1; | |||
n = 2; | |||
for(i=c*L;i<S-c*L;i++){ | |||
if(i == j*c*L){ | |||
j = j + 1; | |||
if(j%2 == 0){ | |||
ngb[i][0]= i - c*L; | |||
ngb[i][1]= i + 1; | |||
ngb[i][2]= i + c*L; | |||
ngb[i][3]= i + 2*c*L - 1; | |||
ngb[i][4]= i + c*L - 1; | |||
ngb[i][5]= i - 1; | |||
} | |||
else{ | |||
ngb[i][0]= i - c*L + 1; | |||
ngb[i][1]= i + 1; | |||
ngb[i][2]= i + c*L + 1; | |||
ngb[i][3]= i + c*L; | |||
ngb[i][4]= i + c*L - 1; | |||
ngb[i][5]= i - c*L; | |||
} | |||
} | |||
else if(i == n*c*L - 1){ | |||
n = n + 1; | |||
if(n%2 == 0){ | |||
ngb[i][0]= i - 2*c*L + 1; | |||
ngb[i][1]= i - c*L + 1; | |||
ngb[i][2]= i + 1; | |||
ngb[i][3]= i + c*L; | |||
ngb[i][4]= i - 1; | |||
ngb[i][5]= i - c*L; | |||
} | |||
else{ | |||
ngb[i][0]= i - c*L; | |||
ngb[i][1]= i - c*L + 1; | |||
ngb[i][2]= i + c*L; | |||
ngb[i][3]= i + c*L - 1; | |||
ngb[i][4]= i - 1; | |||
ngb[i][5]= i - c*L -1; | |||
} | |||
} | |||
else{ | |||
if(j%2 == 0){ | |||
ngb[i][0]= i - c*L; | |||
ngb[i][1]= i + 1; | |||
ngb[i][2]= i + c*L; | |||
ngb[i][3]= i + c*L - 1; | |||
ngb[i][4]= i - 1; | |||
ngb[i][5]= i - c*L - 1; | |||
} | |||
else{ | |||
ngb[i][0]= i - c*L + 1; | |||
ngb[i][1]= i + 1; | |||
ngb[i][2]= i + c*L + 1; | |||
ngb[i][3]= i + c*L; | |||
ngb[i][4]= i - 1; | |||
ngb[i][5]= i - c*L; | |||
} | |||
} | |||
} | |||
j = j + 1; | |||
ngb[S-c*L][0]= (S - c*L) - c*L; | |||
ngb[S-c*L][1]= (S - c*L) + 1; | |||
ngb[S-c*L][2]= 0; | |||
ngb[S-c*L][3]= c*L - 1; | |||
ngb[S-c*L][4]= (S - c*L) + c*L - 1; | |||
ngb[S-c*L][5]= (S - c*L) - 1; | |||
for(i=(S-c*L+1);i<S-1;i++){ | |||
ngb[i][0]= i - c*L; | |||
ngb[i][1]= i + 1; | |||
ngb[i][2]= i - (j - 1)*c*L; | |||
ngb[i][3]= i - (j - 1)*c*L - 1; | |||
ngb[i][4]= i - 1; | |||
ngb[i][5]= i - c*L - 1; | |||
} | |||
ngb[S-1][0]= (S-1) - c*L; | |||
ngb[S-1][1]= (S-1) - c*L + 1; | |||
ngb[S-1][2]= c*L - 1; | |||
ngb[S-1][3]= c*L - 2; | |||
ngb[S-1][4]= (S-1) - 1; | |||
ngb[S-1][5]= (S-1) - c*L - 1; | |||
return ; | |||
} | |||
int main(void) { | |||
int i, j, n, nn, r, REP, destiny, MCS_MAX, index, rand, PP[N][2], Space[S], Space_CM[S], d, sum[4]; | |||
double Prob, sigma, randf, x, y, aux, CM; | |||
REP = 10; | |||
Prob = 24.0/30.0; | |||
sigma = 0.305; | |||
MCS_MAX = 500000; | |||
//-----------------------------------------------INICIA O RNG--------------------------------------------------------- | |||
srand48(time(NULL)); | |||
seed = start_randomic(); | |||
//-----------------------------------------------MATRIZ DE VIZINHOS--------------------------------------------------- | |||
ngb_creator(); | |||
sb_creator(); | |||
//-----------------------------------------------CRIA O ESTADO INICIAL------------------------------------------------ | |||
for(i=0;i<S;i++){ | |||
Space[i] = 0; | |||
Space_CM[i] = 0; | |||
} | |||
for(i=0;i<N;i++){ | |||
index = S*drand48(); | |||
if(Space[index]==0){ | |||
PP[i][0] = index; | |||
Space[index] = 1; | |||
} | |||
else{ | |||
i = i - 1; | |||
} | |||
} | |||
for(i=0;i<N;i++){ | |||
index = 6*drand48(); | |||
PP[i][1] = index; | |||
} | |||
//-----------------------------------------------DINÂMICA DE MONTE CARLO------------------------------------------------ | |||
for(r=0;r<REP;r++){ | |||
for(n=0;n<MCS_MAX;n++){ | |||
//printf("\nTempo = %d\n", n+1); | |||
for(nn=0;nn<N;nn++){ | |||
index = N*drand48(); | |||
rand = round(sigma*ngaussian()); //checar histograma | |||
// muda polaridade | |||
if(PP[index][1] + rand > 5){ | |||
PP[index][1] = PP[index][1] + rand - 6; | |||
} | |||
else if(PP[index][1] + rand < 0){ | |||
PP[index][1] = PP[index][1] + rand + 6; | |||
} | |||
else{ | |||
PP[index][1] = PP[index][1] + rand; | |||
} | |||
// movimenta | |||
randf = drand48(); | |||
if(Prob >= randf){ | |||
destiny = ngb[PP[index][0]][PP[index][1]]; | |||
if(Space[destiny] == 0){ | |||
Space[PP[index][0]] = 0; | |||
PP[index][0] = destiny; | |||
Space[destiny] = 1; | |||
} | |||
} | |||
else{ | |||
rand = 6*drand48(); | |||
destiny = ngb[PP[index][0]][rand]; | |||
if(Space[destiny] == 0){ | |||
Space[PP[index][0]] = 0; | |||
PP[index][0] = destiny; | |||
Space[destiny] = 1; | |||
} | |||
} | |||
} | |||
} | |||
//-----------------------------------------------CALCULA CENTRO DE MASSA------------------------------------------------ | |||
aux = 0; | |||
j = 0; | |||
for(i=0;i<S;i++){ | |||
if(i == (j+1)*c*L){ | |||
j = j + 1; | |||
} | |||
if(Space[i] == 1){ | |||
aux = aux + (i - j*c*L); | |||
} | |||
} | |||
CM = aux/N; | |||
//printf("Achei o CM=%f\n", CM); | |||
//-----------------------------------------------DESLOCA O SISTEMA------------------------------------------------------ | |||
destiny = round(c*L/2); | |||
index = CM; | |||
d = destiny - 1 - index; | |||
//printf("vou deslocar d=%d\n", d); | |||
for(i=0;i<S;i++){ | |||
if(Space[i]==1){ | |||
destiny = i; | |||
for(j=0; j*j<d*d; j++){ | |||
if(d<0){ | |||
destiny = ngb[destiny][4]; | |||
} | |||
if(d>0){ | |||
destiny = ngb[destiny][1]; | |||
} | |||
} | |||
Space_CM[destiny] = 1; | |||
} | |||
} | |||
//-----------------------------------------------CONTA PARTICULAS NAS SUBCAIXAS-------------------------------------------- | |||
for(i=0; i<h*2; i++){ | |||
sum[i] = 0; | |||
} | |||
for(i=0; i<h*2; i++){ | |||
for(j=0; j<L*L; j++){ | |||
sum[i] = sum[i] + Space_CM[sb[i][j]]; | |||
} | |||
} | |||
printf("%d\t%d\t%d\t%d\n", sum[0], sum[1], sum[2], sum[3]); | |||
/* | |||
//-----------------------------------------------GERA COORDENADAS PARA PLOT------------------------------------------------ | |||
for(i=0;i<h*L;i++){ | |||
aux = (1 + pow(-1,i))/4.0; | |||
for(j=i*c*L;j<(i+1)*c*L;j++){ | |||
y = h*L - i*0.866025403; | |||
x = 1.0*j - i*c*L + aux; | |||
if(Space[j]==1){ | |||
printf("%f\t%f\n", x, y); | |||
} | |||
} | |||
} | |||
*/ | |||
/* | |||
//-----------------------------------------------CHECA MATRIZ DE PARTICULAS------------------------------------------------ | |||
printf("Site\tPolarity\n"); | |||
for(i=0;i<N;i++){ | |||
printf("%d\t%d\n", PP[i][0], PP[i][1]); | |||
} | |||
*/ | |||
/* | |||
//-----------------------------------------------CHECA MATRIZ ESPACIAL----------------------------------------------------- | |||
printf("normal\n"); | |||
nn = 0; | |||
for(i=0;i<h*L;i++){ | |||
for(j=nn*c*L;j<(nn+1)*c*L;j++){ | |||
if(j == ((nn+1)*c*L)-1){ | |||
printf(" %d\n", Space[j]); | |||
} | |||
else{ | |||
printf(" %d", Space[j]); | |||
} | |||
} | |||
nn = nn + 1; | |||
} | |||
//-----------------------------------------------CHECA MATRIZ CENTRALIZADA------------------------------------------------ | |||
printf("\ncentralizada\n"); | |||
// checa matriz espacial no CM | |||
nn = 0; | |||
for(i=0;i<h*L;i++){ | |||
for(j=nn*c*L;j<(nn+1)*c*L;j++){ | |||
if(j == ((nn+1)*c*L)-1){ | |||
printf(" %d\n", Space_CM[j]); | |||
} | |||
else{ | |||
printf(" %d", Space_CM[j]); | |||
} | |||
} | |||
nn = nn + 1; | |||
} | |||
*/ | |||
/* | |||
//-----------------------------------------------CHECA MATRIZ DE VIZINHOS------------------------------------------------ | |||
for (i=0; i<S; i++){ | |||
printf("%d|%d\t%d\t%d\t%d\t%d\t%d\n", i, ngb[i][0], ngb[i][1], ngb[i][2], ngb[i][3], ngb[i][4], ngb[i][5]); | |||
} | |||
*/ | |||
/* | |||
//-----------------------------------------------CHECA MATRIZ DE SUBCAIXAS----------------------------------------------- | |||
for(n=0; n<h*2; n++){ | |||
printf("%d|", n); | |||
for(i=0; i<L*L; i++){ | |||
printf("%d ", sb[n][i]); | |||
} | |||
printf("\n"); | |||
} | |||
*/ | |||
for(i=0;i<S;i++){ | |||
Space_CM[i] = 0; | |||
} | |||
} | |||
return 0; | |||
} | |||
</source> | |||
==Considerações Finais== | |||
Com os resultados totais obtidos no artigo original <ref name = BENJAMIN> </ref> e os resultados parciais deste trabalho, é possível mostrar que um modelo de partículas ativas pode ter um comportamento universal muito semelhante ao comportamento de modelos de matéria usual, nesse caso o modelo de Ising, por mais que possuam propriedades estatísticas ao nível microscópico muito distintas. | |||
Desta forma é possível utilizar muitos resultados já conhecidos e bem estabelecidos da matéria inativa (como transições de fase em sistemas de matéria em equilíbrio termodinâmico) para descrever estes sistemas, de modo à compreender melhor o seu comportamento. | |||
==Referência== | ==Referência== | ||
<references/> | <references/> | ||
Edição atual tal como às 16h39min de 3 de dezembro de 2021
Grupo: Bernardo Boatini e Murilo Kessler Azambuja
Neste trabalho iremos seguir de perto o artigo "Critical motility-induced phase separation belongs to the Ising universality class" [1] de Benjamin Partridge e Chiu Fan Lee.
Introdução
A matéria ativa é um tipo de sistema fora do equilíbrio termodinâmico, onde cada "partícula" ou "agente" do sistema tem a capacidade dissipar energia na forma de forças mecânicas exercidas sobre o ambiente no qual está imerso. Esses sistemas muitas vezes podem exibir vários fenômenos novos, como movimentos coletivos quando exige-se um alinhamento das partículas (como bio-polímeros que se auto organizam, tipo os microtúbulos que são parte do citoesqueleto celular, ou cardumes de peixe, por exemplo), ou os chamados MIPS (Motility-Induced Phase Separation) que são sistemas que apresentam uma mudança de fase física devido à interações entre partículas que proíbem a ocupação simultânea de um volume do espaço além delas apresentarem persistência em uma certa direção de movimento. Nestes sistemas, os agentes possuem a capacidede de auto-propulsão, de forma que a condição de balanço detalhado é quebrada no nível microscópico [1], uma vez que as partículas possuem uma direção preferencial de movimento.Estes tipos de sistema muitas vezes podem ser tratados a partir de uma abordagem hidrodinâmica, na qual são chamados de fluidos ativos, e divergem do comportamento usual de fluidos compostos de matéria usual inativa, os quais são descritos pela equação de Navier-Stokes.
Apesar desses sistemas fundamentalmente quebrarem a condição do balanço detalhado, ainda não é claro se o comportamento estatístico universal de sistemas de fluidos ativos necessariamente divergem daqueles de sistemas em equilíbrio. A investigação de comportamentos universais nestes tipos de sistema, além de ser um interece central na física, também pode nos permitir utilizar conhecimentos já bem estabelecidos (como a transição de fase em sistemas de matéria em equilíbrio termodinâmico) para descrever sistemas novos. Neste trabalho foi reproduzido o artigo [1] onde foi investigada o comportamento crítico de um sistema com MIPS e se viu que este tipo de sistema pertence à classe de universalidade de sistemas em equilíbrio como o modelo de Ising para spin. Para tal, foi utilizada três abordagens diferentes: um modelo hidrodinâmico, uma descrição baseada em teoria de campos e a simulação de um modelo de rede hexagonal.
Modelo
O sistema geral que estamos interessados em descrever é constituído de um conjunto de partículas em um meio com friccção, i.e, em um sistema sem conservação de momentum e com interações que não permitem a ocupação simultânea de duas partículas em um mesmo sítio (FIG. 1).
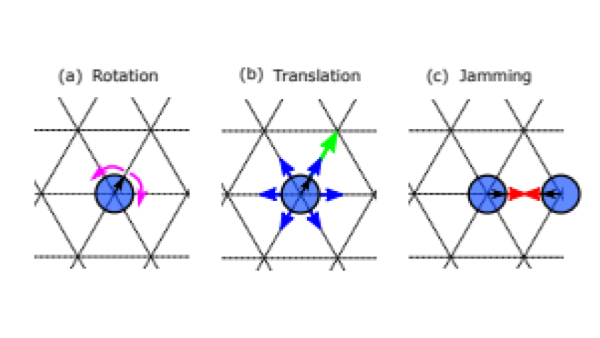
Uma forma de modelar este sistema é considerá-lo um fluido ativo polar e compressível sem interações de alinhamento entre partículas, de forma que não se espera observar movimentos coletivos. Tal sistema é descrito de forma contínua pela chamada equação de Toner-Tu [1].
De um ponto de vista microscópico, podemos usar uma formulação discreta baseada na teoria de campos. Neste caso, consideramos uma rede hexagonal bidimensional, com o numero de ocupação de cada sítio da rede restringido por uma constante (futuramente diremos que , de forma que apenas uma partícula pode ocupar cada sítio).
Modelo no Continuo
As equações de Tuner-Tu para o modelo em questão são dadas por [1]
onde é o campo de densidade de massa e é o campo de densidade de momentum. A equação (1a) diz respeito à conservação de massa do sistema como um todo. A equação (1b) se assemelha muito à equação de Navier-Stokes, assim podemos ver que o primeiro termo da equação caracteriza a compressibilidade do fluido, o segundo termo representa uma difusão do campo de momentum (o sinal negativo indica que o campo de momentum diminui com o passar do tempo), o terceiro termo representa a viscosidade do fluido e é um ruído Gaussiano com estatísticas espaço-temporais dadas por
onde é a intensidade do ruído.
No mesmo artigo [1] os autores argumentam que, devido à ausência de interações de alinhamento entre partículas, a emergência de movimento coletivo é impossível. Por este motivo, temos que o campo de densidade de momentum deve ir à zero no limite hidrodinâmico, de forma que não é uma variável livre e pode ser escrita em função de . Desta forma, [1] obtêm que
de modo que, ao substituir em (1a), temos
onde para alguma constante e é o Hamiltoniano de Ginzburg-Landau. A partir da equação (2), vemos que é possível descrever o sistema a partir da manipulação de dois parâmetros principais: o campo de densidade de partículas (ou , a menos de uma constante) e a intensidade do ruído .
Modelo no Espaço Discreto
Como já foi dito antes, no modelo discreto é utilizado uma rede bidimensional hexagonal com número de ocupação máximo para cada sítio da rede. Os agentes são divididos em seis tipos distintos de partículas ativas, cada uma se move em uma direção (as diagonais do hexágono) e somente vai saltar para o sítio adjacente ao longo desta direção, com uma taxa que depende da ocupação do sítio em questão. Além disso, é possível que uma partícula se transforme em outra, com uma taxa , correspondendo assim a um ruído rotacional de cada partícula. Utilizando a notação utilizada em [1], temos que a rede hexagonal é caracterizado pelo conjunto de vetores e a orientação ou tipo da partícula ativa pelo índice . Desta forma o número de partículas do tipo ocupando o sítio da rede é denotado por . Com o formalismo desenvolvido em [2], temos que a teoria de campos nos fornece uma ação dada por
onde é o número de partículas total ocupando o sítio . A segunda linha da equação (3) diz respeito ao termo de transição entre uma posição e uma posição na rede hexagonal. Esta transição ocorre à uma taxa , de forma que a taxa de transição para o sítio decresce com o aumento do número de partículas ocupando o mesmo. Se o número de partículas ocupando o sítio é , então a taxa de transição é nula, indicando que não será possível que ocorra uma transição para este sítio. Este termo modela as interações de exclusão de volume discutidas anteriormente. Em nosso caso específico tomaremos . Além disso, na terceira linha da equação (3) corresponde à transição de tipo da partícula, i.e., à transição do movimento preferencial da partícula de uma orientação para uma . Esta transição ocorre com uma taxa e a notação indica que a partícula somente trocará para uma orientação que seja adjascente à orientação inicial.
Implementação
Nessa secção serão colocados alguns detalhes da implementação da rede, das medidas e da dinâmica de Monte Carlo.
Algoritmo
A dinâmica de Monte Carlo foi implementada de forma que a cada MCS, N partículas do sistema são selecionadas aleatoriamente:
- Primeiramente a partícula decide se vai mudar seu sentido() sorteando um valor através de uma distribuição gaussiana centrada em 0, com variância igula a intencidade do ruído ;
- A nova direção é dada por Falhou ao verificar gramática (erro de sintaxe): {\displaystyle \theta + d.60°} ;
- Depois disso a partícula tem probabilidade de andar para o sitio vizinho naquela direção(se ele estiver vazio);
- Caso a partícula não decida andar naquela direção, ela se desloca na direção de outro sitio vizinho(se ele estiver vazio) sorteado aleatoriamente(emulando o comportamento difusivo).
Redes Hexagonais
Em modelos do tipo LGCA(Lattice Gas Celular Automata) o tipo de rede, bem como as topologias usadas, podem ser determinantes para as medidas e caracterizações do estado macroscópico. A simetria hexagonal se mostra uma boa alternativa para aumentar os graus de liberdade de uma partícula numa rede, quando comparada com a simetria quadrada. Na geometria hexagonal, assim como na quadrada, todos os sítios vizinhos possuem uma mesma distancia entre si só que com 6 graus de liberdade ao invés de quatro.
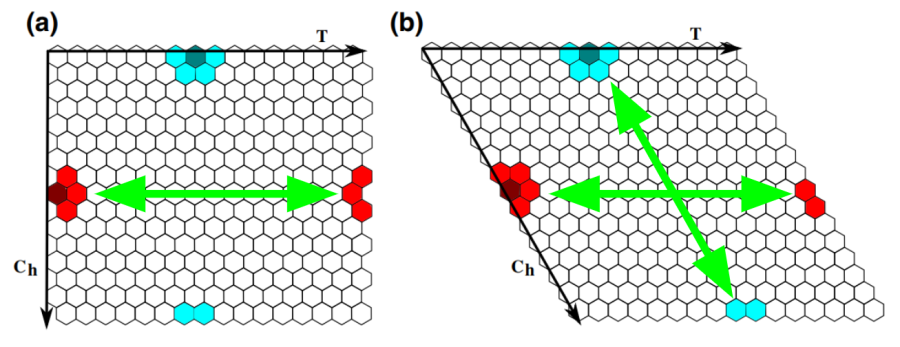
Existem duas topologias possíveis em uma rede hexagonal: "zigzag" e "armchair"[3], e a diferença das duas está principalmente na implementação das condições de contorno periódicas. No caso da topologia em "zigzag"(FIG.2b), o espaço é representado em um paralelogramo, e existem 4 sentidos em que cruzando uma parede a partícula fecha sua trajetória sem ter que cruzar nova mente outra parede do sistema. Na topologia "armchair"(FIG.2a) por outro lado só existem 2 sentidos em que isso acontece.
Sub-Box Sampling Method
O método das subcaixas consiste em dividir o sistema em uma certa quantidade de subsistemas de interesse, permitindo observar as flutuações de densidades, para um valor fixo de partículas no sistema, apenas nessas regiões.
Nesse trabalho o sistema foi dividido em 4 caixas de tamanho : 2 centradas no centro de massa horizontal do sistema e duas centradas na região horizontal "mais rarefeita", que consequentemente esta a uma distancia de do centro de massa.
Quando os parâmetros permitem que haja separação de fase, duas subcaixas ficam posicionadas exatamente sobre o centro da fase liquida e a mesma coisa para a fase gasosa, permitindo uma medição mais precisa das flutuações de densidade sem considerar as regiões de fronteira.
Porém, essas flutuações se tornam especialmente relevantes no ponto crítico, onde o uso de subcaixas se torna muito importante na extração medidas para classificar a transição de fase do modelo em análise.
Medida 1
A primeira medida utilizada para comparar o MIPS com o Ising foi a compressibilidade isotérmica dos subsistemas definida da seguinte forma
onde denota a média do número de partículas contidas em um subsistema de tamanho L.
A compressibilidade isotérmica possui um fator de escala com o tamanho do sistema(), que é conhecido para o caso do Ising 2D ().
Medida 2
A segunda medida proposta é a derivada do cumulante de quarta ordem () com relação a distância adimensional do ponto crítico () calculada no ponto crítico(). O cumulante é definido da seguinte forma
Em [1] é descrito como: "[...] an average over the four sub-boxes of finite size L [...]"
O cumulante de quarta ordem possui a propriedade de ser invariante frente a escala do sistema no ponto crítico(FIG.3), e por isso a sua derivada no ponto critico se torna um fator de escala importante para comparar o estado macroscópico do MIPS e do Ising.
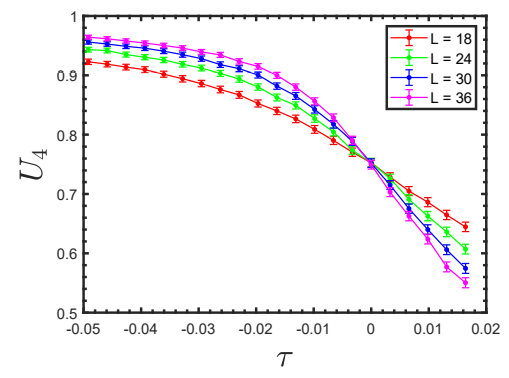
Em a derivada do cumulante de quarta ordem, com respeito a , possui um fator de escala Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha L^{1/ \nu} } , que também pode ser encontrado no modelo de Ising(Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu = 1 } ).
Resultados
Com base nos Diagrama de Fase do sistema(FIG.4) foi possivel extrair os parâmetros característicos dos principais comportamentos do sistema, e testar a simulação nesses diferentes casos. O tempo de relaxação do sistema Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{relax} = 5\times10^5 MCS } (medido a partir do tem pode correlação) foi o mesmo utilizado no artigo. a densidade do sistema foi fixada em Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = 0.522} em todos as simulações. Embora o artigo [1] não especifique a topologia de rede utilizada, nesta análise foi adotada a topologia "armchair".
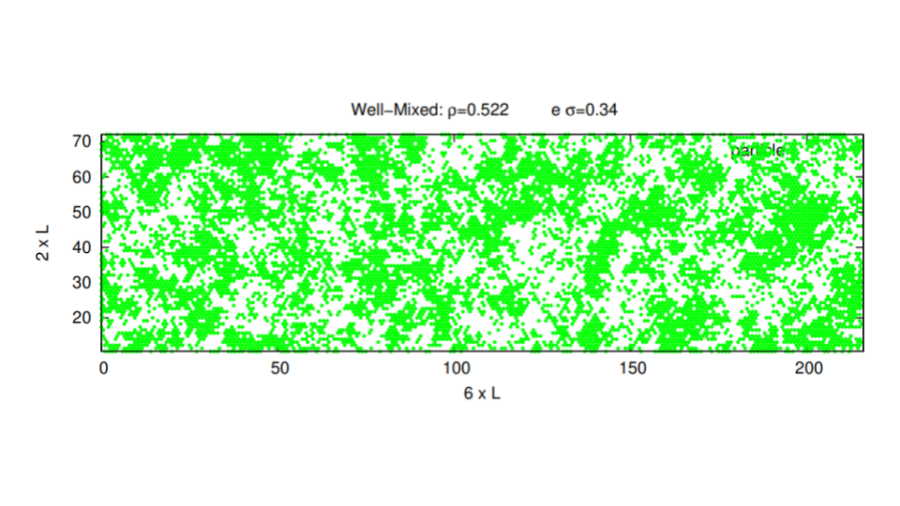
No estado de equilíbrio, após o Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{relax}} , para Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = 0.34} tem-se um comportamento visualmente mais homogêneo(FIG.5), onde o ruído é tão intenso que nenhuma fase é formada no sistema.
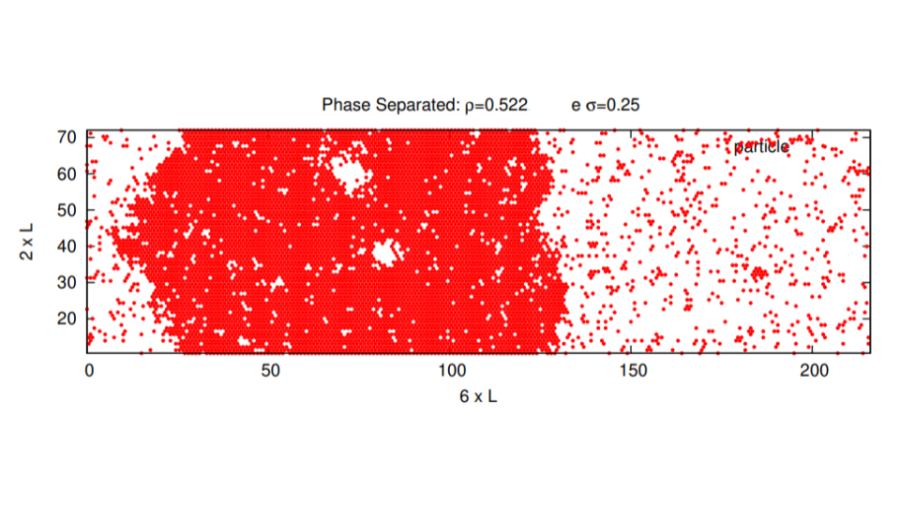
Quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = 0.25} é possível simular um estado estacionário, após Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{relax}} , em que ocorre separação de fase. Na figura 6 é evidente a distinção entre fase densa e fase rarefeita.
Nesses dois casos nenhum dado de ocupação(e consequentemente densidade) das subcaixas foi extraído.
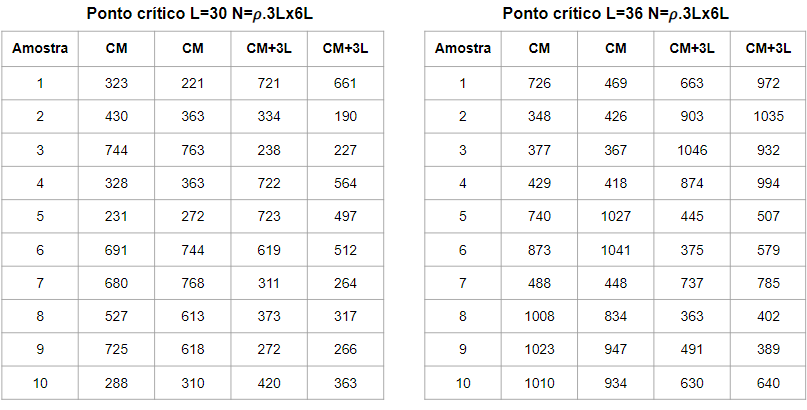
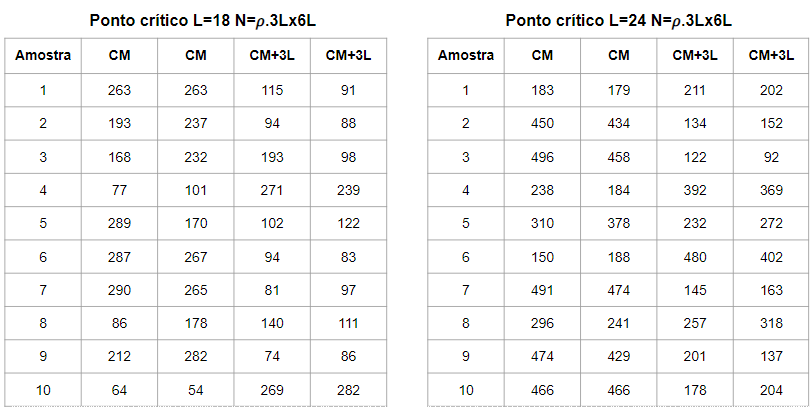
Por fim, temos uma imagem do sistema(FIG.7) em ponto crítico Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = 0.305} , onde qualitativamente constata-se que a fase densa e a fase rarefeita não são distinguíveis no sistema e ambas não encontram uma região de estabilidade ao longo da simulação. Além disso, as flutuações de densidade nas subcaixas, que podem ser medidas através do numero de partículas em cada subcaixa(TABELAS 1 e 2) dividido pela área de cada uma, são, em princípio, diferentes, e isso que permite as análises do fator de escala que virão a seguir.
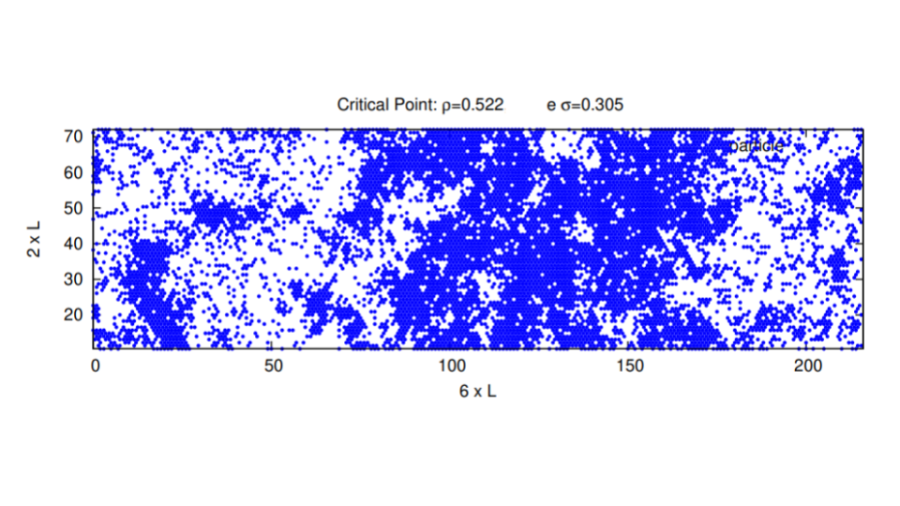
Para realizar a comparação dos fatores de escala 10 amostras independentes(amostradas a cada Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{relax}} ) foram medidas em 4 tamanhos de rede diferentes L = {18, 24, 30, 36}, em cada uma das 10 amostras, 4 subcaixas mediram o número de partículas em diferentes estados estacionários(TABELAS 1 e 2). A análise de dados com respeito a Medida 1 são apresentados na FIGURA 8.
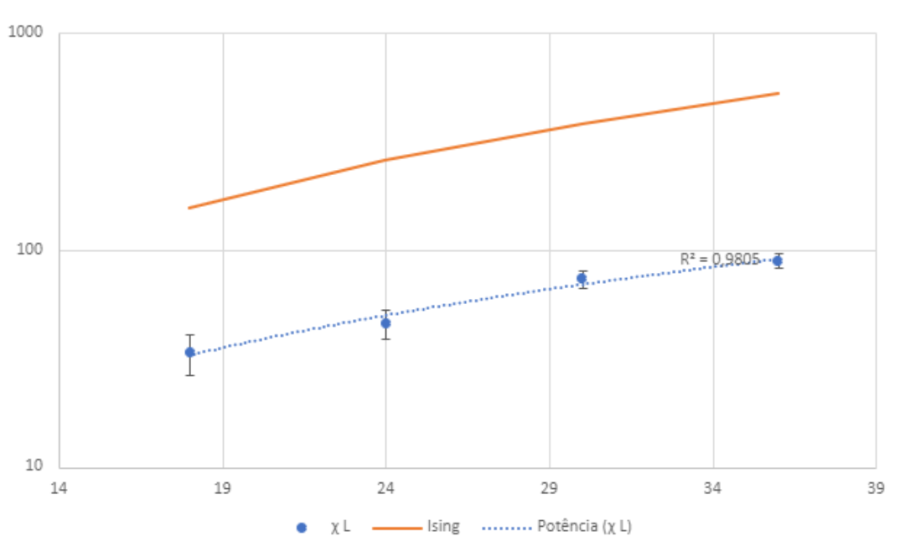
É possível ver, que com uma precisão de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle R^2 = 0.9805} a tendência de escala do Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Chi_L} do sistema de partículas ativas(aproximadamente Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha L^{1.4714}} ) é similar a lei de potência do Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Chi_L} no Ising 2D.
Os dados nas proximidades do ponto crítico foram extraídos, mas os valores de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_4} resultantes não foram satisfatórios. Aparentemente a definição de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle . \rangle_L} é diferente para as 2 medidas propostas, e por esse motivo a analise de dados foi prejudicada; ou seria necessário uma amostragem com mais de 10 amostra para desprezar o ruído nas medidas, já que em [1] o numero de estados estacionários utilizados na estatística é da ordem de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^3} .
Código
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#include "mc.h"
#define L 30 //L = 18, 24, 30, 36 no papper
#define h 2 //h = 2 no papper
#define c 6 //c = 6 no papper
#define S 10800 //S = (h*L)*(c*L)
#define N 5638 //rho = N/S = 0.522 no papper
int ngb[S][6];
int sb[h*2][L*L];
void sb_creator(void) {
int i, j, n, aux;
//cria subcaixas
for(n=0; n<h*2; n++){
j = 0;
aux = n*c*L*L + (c*L/2 - L/2 + j*c*L);
if(n<h){
for(i=0; i<L*L; i++){
if(i == (j+1)*L){
j = j+1;
}
aux = n*c*L*L + (c*L/2 - L/2 + j*c*L);
sb[n][i] = aux + i - j*L;
}
}
else{
aux = h*2 - (n+1);
for(i=0; i<L*L; i++){
if(i == (j+1)*L){
j = j+1;
}
if(i-j*L < L/2){
sb[n][i] = sb[aux][i] + c*L/2;
}
if(i-j*L >= L/2){
sb[n][i] = sb[aux][i] - c*L/2;
}
}
}
}
}
void ngb_creator(void) {
int i, j, n;
//cria matriz de vizinhos
ngb[0][0]= S - c*L + 1; //superior direita
ngb[0][1]= 1; //direita
ngb[0][2]= c*L + 1; //inferior direita
ngb[0][3]= c*L; //inferior esquerda
ngb[0][4]= c*L - 1; //esquerda
ngb[0][5]= S - c*L; //superior esquerda
for(i=1;i<c*L-1;i++){
ngb[i][0]= i + S - c*L + 1;
ngb[i][1]= i + 1;
ngb[i][2]= i + c*L + 1;
ngb[i][3]= i + c*L;
ngb[i][4]= i - 1;
ngb[i][5]= i + S - c*L;
}
ngb[c*L-1][0]= S - c*L;
ngb[c*L-1][1]= 0;
ngb[c*L-1][2]= c*L;
ngb[c*L-1][3]= 2*c*L - 1;
ngb[c*L-1][4]= c*L - 2;
ngb[c*L-1][5]= S - 1;
j = 1;
n = 2;
for(i=c*L;i<S-c*L;i++){
if(i == j*c*L){
j = j + 1;
if(j%2 == 0){
ngb[i][0]= i - c*L;
ngb[i][1]= i + 1;
ngb[i][2]= i + c*L;
ngb[i][3]= i + 2*c*L - 1;
ngb[i][4]= i + c*L - 1;
ngb[i][5]= i - 1;
}
else{
ngb[i][0]= i - c*L + 1;
ngb[i][1]= i + 1;
ngb[i][2]= i + c*L + 1;
ngb[i][3]= i + c*L;
ngb[i][4]= i + c*L - 1;
ngb[i][5]= i - c*L;
}
}
else if(i == n*c*L - 1){
n = n + 1;
if(n%2 == 0){
ngb[i][0]= i - 2*c*L + 1;
ngb[i][1]= i - c*L + 1;
ngb[i][2]= i + 1;
ngb[i][3]= i + c*L;
ngb[i][4]= i - 1;
ngb[i][5]= i - c*L;
}
else{
ngb[i][0]= i - c*L;
ngb[i][1]= i - c*L + 1;
ngb[i][2]= i + c*L;
ngb[i][3]= i + c*L - 1;
ngb[i][4]= i - 1;
ngb[i][5]= i - c*L -1;
}
}
else{
if(j%2 == 0){
ngb[i][0]= i - c*L;
ngb[i][1]= i + 1;
ngb[i][2]= i + c*L;
ngb[i][3]= i + c*L - 1;
ngb[i][4]= i - 1;
ngb[i][5]= i - c*L - 1;
}
else{
ngb[i][0]= i - c*L + 1;
ngb[i][1]= i + 1;
ngb[i][2]= i + c*L + 1;
ngb[i][3]= i + c*L;
ngb[i][4]= i - 1;
ngb[i][5]= i - c*L;
}
}
}
j = j + 1;
ngb[S-c*L][0]= (S - c*L) - c*L;
ngb[S-c*L][1]= (S - c*L) + 1;
ngb[S-c*L][2]= 0;
ngb[S-c*L][3]= c*L - 1;
ngb[S-c*L][4]= (S - c*L) + c*L - 1;
ngb[S-c*L][5]= (S - c*L) - 1;
for(i=(S-c*L+1);i<S-1;i++){
ngb[i][0]= i - c*L;
ngb[i][1]= i + 1;
ngb[i][2]= i - (j - 1)*c*L;
ngb[i][3]= i - (j - 1)*c*L - 1;
ngb[i][4]= i - 1;
ngb[i][5]= i - c*L - 1;
}
ngb[S-1][0]= (S-1) - c*L;
ngb[S-1][1]= (S-1) - c*L + 1;
ngb[S-1][2]= c*L - 1;
ngb[S-1][3]= c*L - 2;
ngb[S-1][4]= (S-1) - 1;
ngb[S-1][5]= (S-1) - c*L - 1;
return ;
}
int main(void) {
int i, j, n, nn, r, REP, destiny, MCS_MAX, index, rand, PP[N][2], Space[S], Space_CM[S], d, sum[4];
double Prob, sigma, randf, x, y, aux, CM;
REP = 10;
Prob = 24.0/30.0;
sigma = 0.305;
MCS_MAX = 500000;
//-----------------------------------------------INICIA O RNG---------------------------------------------------------
srand48(time(NULL));
seed = start_randomic();
//-----------------------------------------------MATRIZ DE VIZINHOS---------------------------------------------------
ngb_creator();
sb_creator();
//-----------------------------------------------CRIA O ESTADO INICIAL------------------------------------------------
for(i=0;i<S;i++){
Space[i] = 0;
Space_CM[i] = 0;
}
for(i=0;i<N;i++){
index = S*drand48();
if(Space[index]==0){
PP[i][0] = index;
Space[index] = 1;
}
else{
i = i - 1;
}
}
for(i=0;i<N;i++){
index = 6*drand48();
PP[i][1] = index;
}
//-----------------------------------------------DINÂMICA DE MONTE CARLO------------------------------------------------
for(r=0;r<REP;r++){
for(n=0;n<MCS_MAX;n++){
//printf("\nTempo = %d\n", n+1);
for(nn=0;nn<N;nn++){
index = N*drand48();
rand = round(sigma*ngaussian()); //checar histograma
// muda polaridade
if(PP[index][1] + rand > 5){
PP[index][1] = PP[index][1] + rand - 6;
}
else if(PP[index][1] + rand < 0){
PP[index][1] = PP[index][1] + rand + 6;
}
else{
PP[index][1] = PP[index][1] + rand;
}
// movimenta
randf = drand48();
if(Prob >= randf){
destiny = ngb[PP[index][0]][PP[index][1]];
if(Space[destiny] == 0){
Space[PP[index][0]] = 0;
PP[index][0] = destiny;
Space[destiny] = 1;
}
}
else{
rand = 6*drand48();
destiny = ngb[PP[index][0]][rand];
if(Space[destiny] == 0){
Space[PP[index][0]] = 0;
PP[index][0] = destiny;
Space[destiny] = 1;
}
}
}
}
//-----------------------------------------------CALCULA CENTRO DE MASSA------------------------------------------------
aux = 0;
j = 0;
for(i=0;i<S;i++){
if(i == (j+1)*c*L){
j = j + 1;
}
if(Space[i] == 1){
aux = aux + (i - j*c*L);
}
}
CM = aux/N;
//printf("Achei o CM=%f\n", CM);
//-----------------------------------------------DESLOCA O SISTEMA------------------------------------------------------
destiny = round(c*L/2);
index = CM;
d = destiny - 1 - index;
//printf("vou deslocar d=%d\n", d);
for(i=0;i<S;i++){
if(Space[i]==1){
destiny = i;
for(j=0; j*j<d*d; j++){
if(d<0){
destiny = ngb[destiny][4];
}
if(d>0){
destiny = ngb[destiny][1];
}
}
Space_CM[destiny] = 1;
}
}
//-----------------------------------------------CONTA PARTICULAS NAS SUBCAIXAS--------------------------------------------
for(i=0; i<h*2; i++){
sum[i] = 0;
}
for(i=0; i<h*2; i++){
for(j=0; j<L*L; j++){
sum[i] = sum[i] + Space_CM[sb[i][j]];
}
}
printf("%d\t%d\t%d\t%d\n", sum[0], sum[1], sum[2], sum[3]);
/*
//-----------------------------------------------GERA COORDENADAS PARA PLOT------------------------------------------------
for(i=0;i<h*L;i++){
aux = (1 + pow(-1,i))/4.0;
for(j=i*c*L;j<(i+1)*c*L;j++){
y = h*L - i*0.866025403;
x = 1.0*j - i*c*L + aux;
if(Space[j]==1){
printf("%f\t%f\n", x, y);
}
}
}
*/
/*
//-----------------------------------------------CHECA MATRIZ DE PARTICULAS------------------------------------------------
printf("Site\tPolarity\n");
for(i=0;i<N;i++){
printf("%d\t%d\n", PP[i][0], PP[i][1]);
}
*/
/*
//-----------------------------------------------CHECA MATRIZ ESPACIAL-----------------------------------------------------
printf("normal\n");
nn = 0;
for(i=0;i<h*L;i++){
for(j=nn*c*L;j<(nn+1)*c*L;j++){
if(j == ((nn+1)*c*L)-1){
printf(" %d\n", Space[j]);
}
else{
printf(" %d", Space[j]);
}
}
nn = nn + 1;
}
//-----------------------------------------------CHECA MATRIZ CENTRALIZADA------------------------------------------------
printf("\ncentralizada\n");
// checa matriz espacial no CM
nn = 0;
for(i=0;i<h*L;i++){
for(j=nn*c*L;j<(nn+1)*c*L;j++){
if(j == ((nn+1)*c*L)-1){
printf(" %d\n", Space_CM[j]);
}
else{
printf(" %d", Space_CM[j]);
}
}
nn = nn + 1;
}
*/
/*
//-----------------------------------------------CHECA MATRIZ DE VIZINHOS------------------------------------------------
for (i=0; i<S; i++){
printf("%d|%d\t%d\t%d\t%d\t%d\t%d\n", i, ngb[i][0], ngb[i][1], ngb[i][2], ngb[i][3], ngb[i][4], ngb[i][5]);
}
*/
/*
//-----------------------------------------------CHECA MATRIZ DE SUBCAIXAS-----------------------------------------------
for(n=0; n<h*2; n++){
printf("%d|", n);
for(i=0; i<L*L; i++){
printf("%d ", sb[n][i]);
}
printf("\n");
}
*/
for(i=0;i<S;i++){
Space_CM[i] = 0;
}
}
return 0;
}
Considerações Finais
Com os resultados totais obtidos no artigo original [1] e os resultados parciais deste trabalho, é possível mostrar que um modelo de partículas ativas pode ter um comportamento universal muito semelhante ao comportamento de modelos de matéria usual, nesse caso o modelo de Ising, por mais que possuam propriedades estatísticas ao nível microscópico muito distintas.
Desta forma é possível utilizar muitos resultados já conhecidos e bem estabelecidos da matéria inativa (como transições de fase em sistemas de matéria em equilíbrio termodinâmico) para descrever estes sistemas, de modo à compreender melhor o seu comportamento.
Referência
- ↑ 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 https://arxiv.org/pdf/1810.06112.pdf Benjamin Partridge, Chiu Fan Lee, "CRITICAL MOTILITY-INDUCED PHASE SEPARATION BELONGS TO THE ISING UNIVERSALITY CLASS"
- ↑ Disponível em: https://arxiv.org/pdf/0709.1325.pdf Alexandre Lefèvre, Giulio Biroli, "DYNAMICS OF INTERACTING PARTICLE SYSTEMS: STOCHASTIC PROCESS AND FIELD THEORY"
- ↑ 3,0 3,1 HATZIKIROU, Haralambos et al. Extracting cellular automaton rules from physical Langevin equation models for single and collective cell migration. Journal of Mathematical Biology, [s. l.], 2017.









![{\displaystyle \mathbf {g} =-\nabla {\Big [}(a_{1}\phi +a_{2}\phi ^{2}+a_{3}\phi ^{3})-(\nabla ^{2}(b\phi )){\Big ]}+\mathbf {f} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc4e730b5fc0783cd2d044d34bb388a8f7c838ef)











![{\displaystyle -\gamma {\Big (}M-N_{\mathbf {R} +\mathbf {e} _{\theta _{i}}}{\Big )}A_{\mathbf {R} }^{\theta _{i}}{\Big (}e^{{\hat {A}}_{\mathbf {R} +\mathbf {e} _{\theta _{i}}}^{\theta _{i}}-{\hat {A}}_{\mathbf {R} }^{\theta _{i}}}-1{\Big )}{\Bigg ]}\qquad (3)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/921d95fa1837e08639c5db9211f62cc6a963f36a)