Transições de Fase: mudanças entre as edições
Sem resumo de edição |
Sem resumo de edição |
||
| (24 revisões intermediárias por 2 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
Trabalho desenvolvido no semestre 2021/1 da UFRGS pelos alunos Kevin Pergher, Lucas Colombo e Mateus Guimarães para o curso de Métodos Computacionais da Física C, ministrado pelo professor Heitor C.M Fernandes. | Trabalho desenvolvido no semestre 2021/1 da UFRGS pelos alunos Kevin Pergher, Lucas Colombo e Mateus Guimarães para o curso de Métodos Computacionais da Física C, ministrado pelo professor Heitor C.M Fernandes. | ||
== Introdução == | == Introdução == | ||
Uma transição de fase é uma mudança brusca nas características físicas de um meio com a variação de um parâmetro - por exemplo, a mudança brusca de densidade quando um líquido se torna um gás com um aumento de temperatura. Estas usualmente se encontram associadas à passagem do sistema de um estado com mais ordem para um estado com menos ordem, ou vice versa. | |||
Uma maneira de caracterizar estas transições é a partir de observáveis já conhecidos que sejam atrelados a uma característica intrínseca do meio. Tais observáveis recebem o nome de [[Transições de Fase#Parâmetros de Ordem|parâmetros de ordem]]. | |||
Uma transição de fase nem sempre está associada a uma mudança de estado físico. É necessário a variação brusca de um observável, que nem sempre é imediatamente visível -por exemplo, a magnetização de um ferromagnético. | |||
== Parâmetros de Ordem == | |||
Um observável que | |||
:'''i.''' Preferencialmente, ser diferente de 0 na fase ordenada; | |||
:'''ii.''' Preferencialmente, ser igual a 0 na fase ordenada. | |||
Pode ser usado para caracterizar uma transição de fase. Tais observáveis são denominados parâmetros de ordem [2]. É importante notar que em muitos casos, um observável pode passar a cumprir estes parâmetros com uma translação. | |||
Existem diversos exemplos de parâmetros ordem associados às mais diversas áreas, como por exemplo: | |||
Em um sistema ferromagnético, a magnetização é zero na fase desordenada e possui algum valor positivo na fase ordenada. | |||
Em sistemas gás-líquido, o negativo da diferença de densidade entre a fase líquida e a fase gasosa é zero na fase líquida, e algum valor positivo na fase gasosa. | |||
Em sistemas de cristais líquidos, o grau da ordem de orientação. | |||
== Transições de Primeira e Segunda Ordem == | |||
As transições de fase podem ser classificadas em função da natureza da derivada da energia livre do sistema. Seguindo a notação de [https://pt.wikipedia.org/wiki/Paul_Ehrenfest Ehrenfest], temos: | |||
=== Transição de Primeira Ordem === | |||
Uma transição de primeira ordem é definida a partir de uma descontinuidade em uma função representada por derivadas primeiras da função de energia livre do sistema, ou seja, se um observável calculado a partir de uma derivada da função de energia livre do sistema apresentar uma descontinuidade, define-se uma transição de fase de primeira ordem neste ponto de descontinuidade. | |||
Exemplos de observáveis que apresentam transições de primeira ordem são: | |||
{| class="wikitable" style="height:14em;" | |||
|- | |||
! Entropia (<math> S </math>) !! Volume Molar (<math> V_m </math>) !! Entalpia (<math> H </math>) | |||
|- style=height:7em | |||
| <math>\bigg( \frac{\partial F}{\partial T}\bigg)_{P} = -S</math> || <math>\bigg( \frac{\partial F}{\partial T}\bigg)_{T} = V_m</math> || <math>\bigg( \frac{\partial \frac{F}{T}}{\partial \frac{1}{T}}\bigg)_{P} = H</math> | |||
|} | |||
Onde <math>F</math> é a energia livre de Helmholtz | |||
=== Transição de Segunda Ordem === | |||
Uma transição de segunda ordem está relacionado com descontinuidades em derivadas segundas da função de energia livre do sistema, ou seja, ao invés de apresentar descontinuidades nas primeiras derivadas, as transições de fase de segunda ordem apresentam descontinuidades em relação a derivadas segundas da função de energia livre. | |||
Exemplos de observáveis que apresentam transições de segunda ordem são: | |||
{| class="wikitable" style="height:14em" align="center"; | |||
|- | |||
! Calor Específico ( <math> C_p </math> ) !! Coeficiente de Expansão Térmica ( <math>\alpha </math> ) !! Coeficiente de Compressibilidade Isotérmica ( <math> \kappa_T </math> ) | |||
|- style=height:7em | |||
| <math>\bigg( \frac{\partial H}{\partial T}\bigg)_{P} = C_p</math> || <math>\bigg( \frac{\partial V}{\partial T}\bigg) = \alpha V</math> || <math>\bigg( \frac{\partial F}{\partial T}\bigg)_{T} = -\kappa_T V</math> | |||
|} | |||
Estas transições apresentam um ponto de inflexão na denominada temperatura crítica (T_c) do sistema. Assim, é possível separar dois estados com temperatura <math>T</math> : | |||
:<math>T < T_c =</math> Estado Ordenado; | |||
:<math>T > T_c =</math> Estado Desordenado. | |||
=== Transição de Ordens Maiores === | |||
A definição de Ehrenfest permite a existência de transições de ordens maiores, correspondendo a a derivadas de ordens maiores da função de energia livre do sistema. Também existem as chamadas ''transições de ordem infinita'' ou ''transições contínuas''[3], nas quais uma transição de fase é perceptível macroscopicamente, porém não existem descontinuidades em derivadas finitas da função de energia livre. | |||
== Transições de Fase em Simulações == | |||
O [https://fiscomp.if.ufrgs.br/index.php/Grupo_-_Modelo_de_Potts Modelo de Potts] com q estados é uma simulação relativamente simples que apresenta transições de fase tanto de primeira ordem como contínuas: de primeira ordem se <math> q > 4</math>, e de ordem infinita se <math> q \leqslant 4</math>. | |||
Utilizando o [https://fiscomp.if.ufrgs.br/index.php/Clusteriza%C3%A7%C3%A3o Algoritmo de Wolff] para medir o parâmetro de ordem escolhido (magnetização do sistema), obteve-se a seguinte série temporal: | |||
[Série Temporal] | |||
[[Arquivo:q=4.jpg|1000px]] | |||
[[Arquivo:q=10.jpg|1000px]] | |||
O caso de q = 4 apresenta uma transição comparativamente suave, sem pontos ruscos de inflexão. Isto é característico de transições contínuas: não há descontinuidades nos observáveis. O caso q = 10 apresenta uma transição extremamente brusca, característica de transições de 1a ordem. | |||
== Referências == | |||
[1] Challa MS, Landau DP, Binder K. '''Finite-size effects at temperature-driven first-order transitions'''. Phys Rev B Condens Matter. 1986 Aug 1;34(3):1841-1852. doi: 10.1103/physrevb.34.1841. PMID: 9939842. | |||
[2] Chen S, Ferrenberg AM, Landau DP. '''Monte Carlo simulation of phase transitions in a two-dimensional random-bond Potts model'''. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1995 Aug;52(2):1377-1386. doi: 10.1103/physreve.52.1377. PMID: 9963557 | |||
[3] Kumar, Pradeep & Khare, Avinash & Saxena, Avadh. (2011). '''An Infinite Order Phase Transition.''' | |||
Edição atual tal como às 23h14min de 1 de dezembro de 2021
Trabalho desenvolvido no semestre 2021/1 da UFRGS pelos alunos Kevin Pergher, Lucas Colombo e Mateus Guimarães para o curso de Métodos Computacionais da Física C, ministrado pelo professor Heitor C.M Fernandes.
Introdução
Uma transição de fase é uma mudança brusca nas características físicas de um meio com a variação de um parâmetro - por exemplo, a mudança brusca de densidade quando um líquido se torna um gás com um aumento de temperatura. Estas usualmente se encontram associadas à passagem do sistema de um estado com mais ordem para um estado com menos ordem, ou vice versa. Uma maneira de caracterizar estas transições é a partir de observáveis já conhecidos que sejam atrelados a uma característica intrínseca do meio. Tais observáveis recebem o nome de parâmetros de ordem. Uma transição de fase nem sempre está associada a uma mudança de estado físico. É necessário a variação brusca de um observável, que nem sempre é imediatamente visível -por exemplo, a magnetização de um ferromagnético.
Parâmetros de Ordem
Um observável que
- i. Preferencialmente, ser diferente de 0 na fase ordenada;
- ii. Preferencialmente, ser igual a 0 na fase ordenada.
Pode ser usado para caracterizar uma transição de fase. Tais observáveis são denominados parâmetros de ordem [2]. É importante notar que em muitos casos, um observável pode passar a cumprir estes parâmetros com uma translação. Existem diversos exemplos de parâmetros ordem associados às mais diversas áreas, como por exemplo: Em um sistema ferromagnético, a magnetização é zero na fase desordenada e possui algum valor positivo na fase ordenada. Em sistemas gás-líquido, o negativo da diferença de densidade entre a fase líquida e a fase gasosa é zero na fase líquida, e algum valor positivo na fase gasosa. Em sistemas de cristais líquidos, o grau da ordem de orientação.
Transições de Primeira e Segunda Ordem
As transições de fase podem ser classificadas em função da natureza da derivada da energia livre do sistema. Seguindo a notação de Ehrenfest, temos:
Transição de Primeira Ordem
Uma transição de primeira ordem é definida a partir de uma descontinuidade em uma função representada por derivadas primeiras da função de energia livre do sistema, ou seja, se um observável calculado a partir de uma derivada da função de energia livre do sistema apresentar uma descontinuidade, define-se uma transição de fase de primeira ordem neste ponto de descontinuidade.
Exemplos de observáveis que apresentam transições de primeira ordem são:
| Entropia () | Volume Molar () | Entalpia () |
|---|---|---|
Onde é a energia livre de Helmholtz
Transição de Segunda Ordem
Uma transição de segunda ordem está relacionado com descontinuidades em derivadas segundas da função de energia livre do sistema, ou seja, ao invés de apresentar descontinuidades nas primeiras derivadas, as transições de fase de segunda ordem apresentam descontinuidades em relação a derivadas segundas da função de energia livre.
Exemplos de observáveis que apresentam transições de segunda ordem são:
| Calor Específico ( ) | Coeficiente de Expansão Térmica ( ) | Coeficiente de Compressibilidade Isotérmica ( ) |
|---|---|---|
Estas transições apresentam um ponto de inflexão na denominada temperatura crítica (T_c) do sistema. Assim, é possível separar dois estados com temperatura :
- Estado Ordenado;
- Estado Desordenado.
Transição de Ordens Maiores
A definição de Ehrenfest permite a existência de transições de ordens maiores, correspondendo a a derivadas de ordens maiores da função de energia livre do sistema. Também existem as chamadas transições de ordem infinita ou transições contínuas[3], nas quais uma transição de fase é perceptível macroscopicamente, porém não existem descontinuidades em derivadas finitas da função de energia livre.
Transições de Fase em Simulações
O Modelo de Potts com q estados é uma simulação relativamente simples que apresenta transições de fase tanto de primeira ordem como contínuas: de primeira ordem se , e de ordem infinita se .
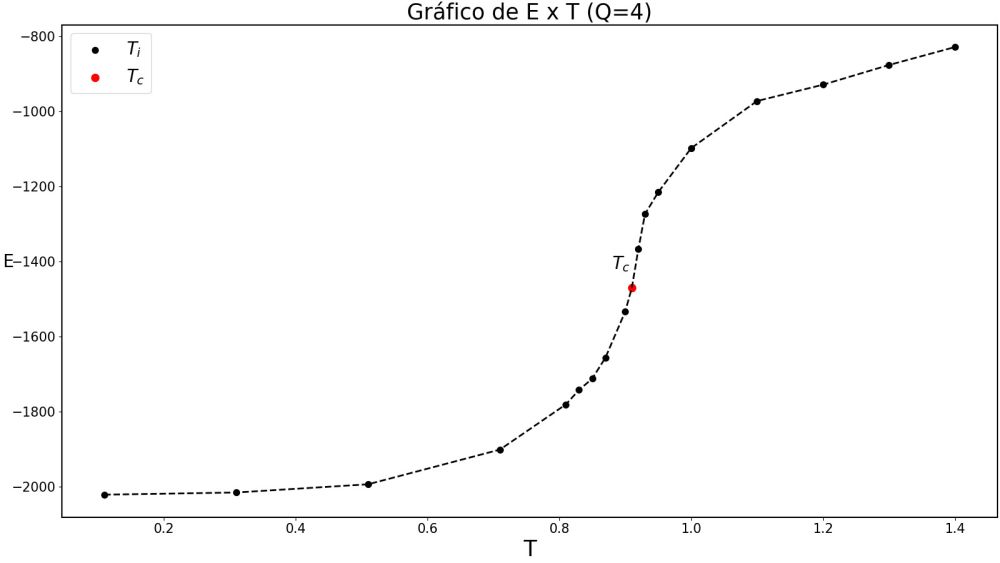
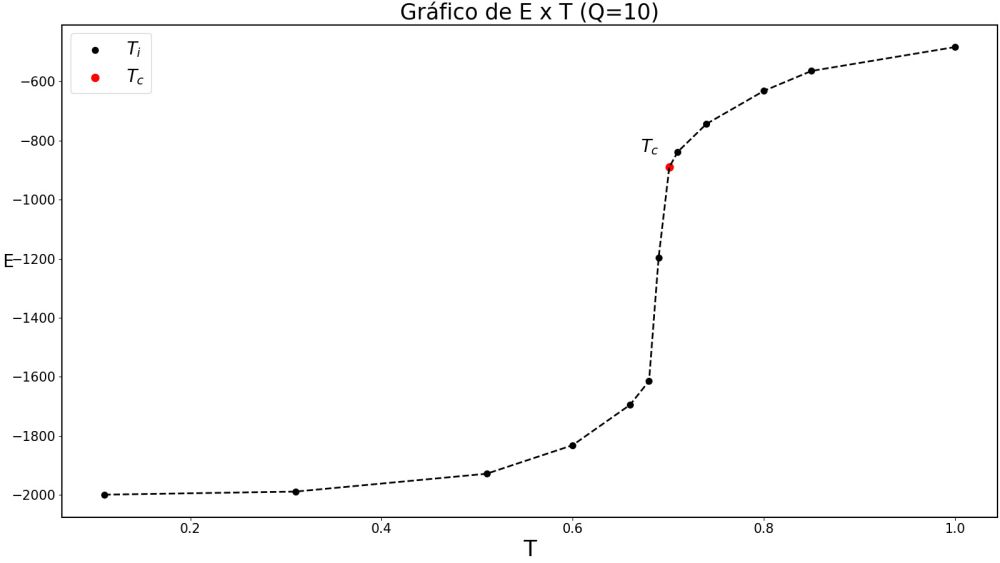
Utilizando o Algoritmo de Wolff para medir o parâmetro de ordem escolhido (magnetização do sistema), obteve-se a seguinte série temporal:
[Série Temporal]
O caso de q = 4 apresenta uma transição comparativamente suave, sem pontos ruscos de inflexão. Isto é característico de transições contínuas: não há descontinuidades nos observáveis. O caso q = 10 apresenta uma transição extremamente brusca, característica de transições de 1a ordem.
Referências
[1] Challa MS, Landau DP, Binder K. Finite-size effects at temperature-driven first-order transitions. Phys Rev B Condens Matter. 1986 Aug 1;34(3):1841-1852. doi: 10.1103/physrevb.34.1841. PMID: 9939842.
[2] Chen S, Ferrenberg AM, Landau DP. Monte Carlo simulation of phase transitions in a two-dimensional random-bond Potts model. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1995 Aug;52(2):1377-1386. doi: 10.1103/physreve.52.1377. PMID: 9963557
[3] Kumar, Pradeep & Khare, Avinash & Saxena, Avadh. (2011). An Infinite Order Phase Transition.