Modelos Epidemiológicos: mudanças entre as edições
Sem resumo de edição |
|||
| (203 revisões intermediárias por 3 usuários não estão sendo mostradas) | |||
| Linha 1: | Linha 1: | ||
''' | Grupo: Gabriel Schmökel, Julia Remus e Luis Gustavo Lang Gaiato | ||
O objetivo do trabalho é realizar a implementação do modelo [https://en.wikipedia.org/wiki/Compartmental_models_in_epidemiology SIR] ('''''S'''uscetível, '''I'''nfectado e '''R'''ecuperado'') e de um modelo simplificado do proposto pelo artigo "''An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics''" <ref name="multiple">AMARAL, Marco; OLIVEIRA, Marcelo de; JAVARONE, Marco, ''An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics''. arXiv:2008.05979v2 [physics.soc-ph] .</ref> utilizando Monte Carlo. Espera-se obter ondas de infecção quando utilizado o processo de quarentena voluntária, tal qual observada pelos dados da Covid-19 e encontrada pelo artigo de referência do modelo. | |||
Será apresentada uma breve introdução sobre o tema e as equações que envolvem o desenvolvimento dos cálculos, as implementações e seus respectivos resultados. São deixados alguns objetivos futuros para um trabalho posterior. | |||
== Introdução == | |||
A pandemia atual mostrou que táticas para mitigar o avanço da doença dependem não só de medidas governamentais, mas também da percepção do indivíduo nesse meio. <ref name="introref">SIEGRIST, Michael;BERTH, Angela. ''Worldviews, trust, and risk perceptions shape public acceptance of COVID-19 public health measures''. DOI: https://doi.org/10.1073/pnas.2100411118.</ref>. Essa percepção depende da métrica utilizada por cada pessoa, levando em consideração fatores como: prejuízos psicológicos, situação econômica, o entendimento sobre o que é certo (como a sociedade o enxerga, quais as verdades que são consideradas pelo indivíduo), a escolha pelo bem comum, entre outros. A visão do indivíduo pode mudar ao longo do tempo e, com isso, modificar como a doença evolui - como é quantificado pela formação de ondas de infecção atualmente. <ref name="nature">BAVEL, Jay; et al, ''Using social and behavioural science to support COVID-19 pandemic response''. DOI: https://doi.org/10.1038/s41562-020-0884-z .</ref> | |||
A fim de simular esses cenários de pandemia com e sem a percepção do indivíduo, propõe-se um trabalho com o '''objetivo''' de realizar a implementação do modelo [https://en.wikipedia.org/wiki/Compartmental_models_in_epidemiology SIR] e de um modelo simplificado do proposto pelo artigo "''An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics''" <ref name="multiple">AMARAL, Marco; OLIVEIRA, Marcelo de; JAVARONE, Marco, ''An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics''. arXiv:2008.05979v2 [physics.soc-ph] .</ref> utilizando Monte Carlo. | |||
O | O modelo apresentado por Marco Amaral, et al <ref name="multiple">AMARAL, Marco; OLIVEIRA, Marcelo de; JAVARONE, Marco, ''An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics''. arXiv:2008.05979v2 [physics.soc-ph] .</ref> propõe que o indivíduo escolha adequar-se a uma das estratégias da quarentena (fazer ou não) dependendo do risco que observa a partir da quantidade de infectados no sistema. Acoplada à escolha da estratégia, está o modelo SIR com parâmetros distintos para indivíduos não isolados e isolados. Para a solução, os autores utilizam a [https://en.wikipedia.org/wiki/Mean-field_theory teoria de campo médio], obtendo ondas de infecção ao longo do tempo. | ||
Neste trabalho, a escolha da estratégia pelo indivíduo se dará de acordo com o estado dos seus vizinhos mais próximos - utilizado o [https://pt.wikipedia.org/wiki/Dilema_do_prisioneiro dilema do prisioneiro] - enquanto a evolução dos infectados no sistema será realizada com o modelo SIR, assim como no trabalho citado. Para a simulação foi utilizado o método de Monte Carlo. | |||
= | É esperado obter as ondas de infecção como previsto por Marco Amaral, et al <ref name="multiple">AMARAL, Marco; OLIVEIRA, Marcelo de; JAVARONE, Marco, ''An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics''. arXiv:2008.05979v2 [physics.soc-ph] .</ref> e observadas nos dados reais da Covid-19, ambos os exemplos podem ser observados a seguir. Como o método é diferente, não é esperado que as ondas sejam iguais às do artigo, mas sim, um movimento mais sutil. | ||
<div><ul> | |||
<li style="display: inline-block; vertical-align: top;"> [[File:evolucao-marco-infectados.png|400px|thumb|Resultado do modelo proposto por Marco Amaral, et al <ref name="multiple">AMARAL, Marco; OLIVEIRA, Marcelo de; JAVARONE, Marco, ''An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics''. arXiv:2008.05979v2 [physics.soc-ph] .</ref>]] </li> | |||
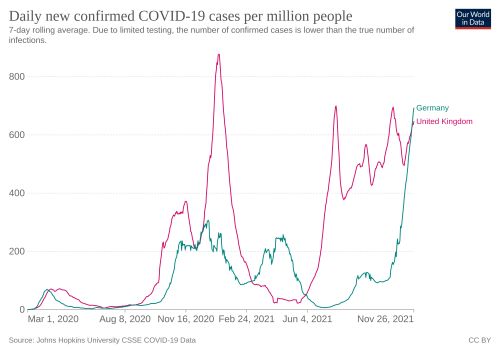
<li style="display: inline-block; vertical-align: top;"> [[File:coronavirus-data-explorer.png|500px|thumb|Casos diários confirmados de Covid-19 a cada um milhão de pessoas no Reino Unido e na Alemanha]]</li> | |||
</ul></div> | |||
No gráfico da direita pode-se observar a quantidade de casos diários (infectados) na Alemanha e no Reino Unido ao longo do tempo, vê-se que existem ondas de infecção. Já no gráfico da direita, é possível observar a solução obtida por Marco Amaral, et al <ref name="multiple">AMARAL, Marco; OLIVEIRA, Marcelo de; JAVARONE, Marco, ''An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics''. arXiv:2008.05979v2 [physics.soc-ph] .</ref>. | |||
O esquemático do modelo SIR com a escolha da quarentena pode ser visto na seção ''Modelo SIR com quarentena voluntária''. | O esquemático do modelo SIR com a escolha da quarentena pode ser visto na seção ''Modelo SIR com quarentena voluntária''. | ||
| Linha 31: | Linha 39: | ||
* Infectado ('''I'''): Número de indivíduos infectados. Indivíduos infectados tem uma probabilidade de infectar indivíduos suscetíveis quando em contato, e uma probabilidade de tornar-se indivíduos removidos a medida que tempo avança. | * Infectado ('''I'''): Número de indivíduos infectados. Indivíduos infectados tem uma probabilidade de infectar indivíduos suscetíveis quando em contato, e uma probabilidade de tornar-se indivíduos removidos a medida que tempo avança. | ||
* Recuperado ou Removido ('''R'''): Número de indivíduos removidos (recuperados ou mortos pela doença). Indivíduos que foram infectados, tornam-se recuperados ou mortos pela doença, desta forma entram na classificação de indivíduos removidos, já que não são mais suscetíveis a pegar a doença, pois adquiriram imunidade. Assumindo que o número de mortos é irrelevante ao se comparar com a população total, então o parâmetro R recebe o nome de indivíduos recuperados ou resistentes. | * Recuperado ou Removido ('''R'''): Número de indivíduos removidos (recuperados ou mortos pela doença). Indivíduos que foram infectados, tornam-se recuperados ou mortos pela doença, desta forma entram na classificação de indivíduos removidos, já que não são mais suscetíveis a pegar a doença, pois adquiriram imunidade. Assumindo que o número de mortos é irrelevante ao se comparar com a população total, então o parâmetro <math>R</math> recebe o nome de indivíduos recuperados ou resistentes. | ||
A dinâmica de uma epidemia geralmente é mais rápida do que os números de nascimentos e óbitos, por essa razão se omite | A dinâmica de uma epidemia geralmente é mais rápida do que os números de nascimentos e óbitos, por essa razão se omite estas quantidades no modelo comportamental simples do SIR. Usando uma população fixa, Kermack e McKendrick chegaram nas seguintes equações diferenciais que descrevem a dinâmica de uma epidemia <ref name=SIR> MCKENDRICK, A.G.; KERMACK, W. O.. Mathematical Theory of Epidemics. Disponível em: https://gallica.bnf.fr/ark:/12148/bpt6k56208r/f728.item.langFR </ref>: | ||
<math> | <math> | ||
| Linha 49: | Linha 57: | ||
O sistema descrito pelas equações acima é não linear, porém é possível derivar uma solução analítica de forma implícita <ref> Harko, Tiberiu; Lobo, Francisco S. N.; Mak, M. K. (2014). "Exact analytical solutions of the Susceptible-Infected-Recovered (SIR) epidemic model and of the SIR model with equal death and birth rates". Applied Mathematics and Computation. 236: 184–194. arXiv:1403.2160. Bibcode:2014arXiv1403.2160H. doi:10.1016/j.amc.2014.03.030. S2CID 14509477 </ref>. | O sistema descrito pelas equações acima é não linear, porém é possível derivar uma solução analítica de forma implícita <ref> Harko, Tiberiu; Lobo, Francisco S. N.; Mak, M. K. (2014). "Exact analytical solutions of the Susceptible-Infected-Recovered (SIR) epidemic model and of the SIR model with equal death and birth rates". Applied Mathematics and Computation. 236: 184–194. arXiv:1403.2160. Bibcode:2014arXiv1403.2160H. doi:10.1016/j.amc.2014.03.030. S2CID 14509477 </ref>. | ||
A população total no SIR é constante, e pode ser | A população total no SIR é constante, e pode ser expressada pela soma total dos indivíduos suscetíveis, infectados e removidos: | ||
<math> | <math> | ||
| Linha 61: | Linha 69: | ||
</math> | </math> | ||
A taxa de transmissão da doença é dada pela variável beta, | A taxa de transmissão da doença é dada pela variável <math>\beta</math>, esta depende de outras duas variáveis, a primeira indica a "transmissibilidade", definida por <math>\tau</math>, a segunda indica o "número médio de contatos" entre infectados e suscetíveis, indicada por <math>\bar c</math>. Portanto, pode-se escrever a taxa de transmissão pela expressão: | ||
<math> | <math> | ||
| Linha 67: | Linha 75: | ||
</math> | </math> | ||
A taxa de remoção da doença, indicada por | A taxa de remoção da doença, indicada por <math>\gamma</math>, é o inverso do período infeccioso, indicada por <math>d</math>, que o indivíduo permanecerá doente. Note, que quanto maior o período infeccioso, mais demorada é a remoção de Infectados para Removidos. | ||
<math> | <math> | ||
| Linha 75: | Linha 83: | ||
==== Dinâmica do Modelo SIR e o Número de Reprodução ==== | ==== Dinâmica do Modelo SIR e o Número de Reprodução ==== | ||
O número básico de reprodução, <math> R_0 </math>, corresponde ao número médio de pessoas que serão | O número básico de reprodução, <math> R_0 </math>, corresponde ao número médio de pessoas que serão contaminadas pela doença quando um indivíduo infectado é introduzido em uma população completamente suscetível <ref name = r0 > M.G.Roberts. The pluses and minuses of r 0 . Journal of the Royal Society interface4, 2007. </ref>. | ||
<math> R_0 = \frac{\beta}{\gamma} | <math> R_0 = \frac{\beta}{\gamma} s_0 \qquad (8) </math> | ||
Conforme o valor de <math> R_0 </math> temos o seguinte comportamento <ref name = r0 > M.G.Roberts. The pluses and minuses of r 0 . Journal of the Royal Society interface4, 2007. </ref>: | Conforme o valor de <math> R_0 </math> temos o seguinte comportamento <ref name = r0 > M.G.Roberts. The pluses and minuses of r 0 . Journal of the Royal Society interface4, 2007. </ref>: | ||
| Linha 85: | Linha 93: | ||
* <math> R_0 < 1 \Rightarrow </math> epidemia decrescente. | * <math> R_0 < 1 \Rightarrow </math> epidemia decrescente. | ||
Pode-se interpretar melhor o comportamento do número de reprodução analisando a curva <math>i(s)</math>. Para obter essa função dividimos a expressão (2) pela expressão (1) na forma normalizada, posteriormente integramos ambos os lados da igualdade, assim chegamos em <ref> Beckley, Ross; Weatherspoon, Cametria; Alexander, Michael; Chandler, Marissa; Johnson, Anthony; Batt, Ghan S. (2013). Modeling epidemics with differential equations. Disponível em: http://www.tnstate.edu/mathematics/mathreu/filesreu/GroupProjectSIR.pdf </ref>: | |||
<math> | <math> i(s) = \frac{\gamma}{\beta}\ln (s) -\frac{\gamma}{\beta}\ln (s_0) -s +1 \qquad (9) </math> | ||
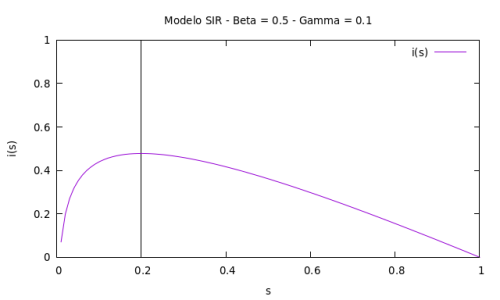
Derivando a expressão (9) em relação a | Derivando a expressão (9) em relação a <math>s</math> observa-se que a função atinge o ponto de máximo quando <math>s = \gamma/\beta</math>. Nas situações em que temos <math>s < \gamma/\beta</math> e <math>s > \gamma/\beta</math>, obtemos respectivamente o comportamento crescente e decrescente para função <math>i(s)</math>. Na sequência é plotada a curva <math>i(s)</math>, observe que o sentido da abscissa <math>s</math> é negativo para o avanço da pandemia. | ||
[[File:I(s).png|500 px|center|thumb|Função do número de indivíduos infectados <math> i </math> em relação ao número de indivíduos suscetíveis <math> s </math>.]] | |||
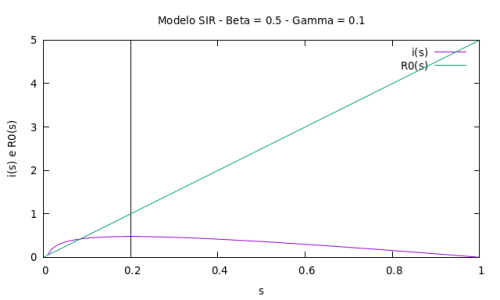
Quando | Quando <math> s </math> esta à direita da reta <math>s = \gamma/\beta</math> a epidemia irá aumentar o seu número de infectados, pois <math> R_0 </math> é maior do que <math>1</math>. O número de infectados irá aumentar até o número de indivíduos suscetíveis ser igual a <math>\gamma/\beta</math>, posteriormente o número de infectados irá decair, pois <math> R_0 </math> é menor do que <math>1</math>. Podemos entender melhor esta informação plotando as curvas i(s) e <math> R_0(s) </math> juntas: | ||
[[File:R0(S).png|500 px|center|thumb|Curva do número de reprodução <math>R_0</math> variando com o número de indivíduos suscetíveis <math> s </math>.]] | |||
=== Modelo SIR com quarentena voluntária === | === Modelo SIR com quarentena voluntária === | ||
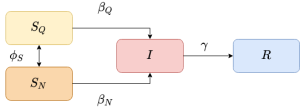
[[File:sir_modificado.png|right|300px|thumb| | [[File:sir_modificado.png|right|300px|thumb|Esquemático modelo SIR com quarentena voluntária em suscetíveis]] | ||
No esquemático pode-se ver o modelo utilizado no trabalho, ele é uma simplificação do artigo escrito por Amaral, et al <ref name="multiple">AMARAL, Marco; OLIVEIRA, Marcelo de; JAVARONE, Marco, ''An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics''. arXiv:2008.05979v2 [physics.soc-ph] .</ref>. Nele temos: | No esquemático pode-se ver o modelo utilizado no trabalho, ele é uma simplificação do artigo escrito por Amaral, et al <ref name="multiple">AMARAL, Marco; OLIVEIRA, Marcelo de; JAVARONE, Marco, ''An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics''. arXiv:2008.05979v2 [physics.soc-ph] .</ref>. Nele temos: | ||
* Componentes suscetíveis podem estar ou não em quarentena. A probabilidade <math>\phi_S</math> para a escolha da | * Componentes suscetíveis podem estar ou não em quarentena. A probabilidade <math>\phi_S</math> para a escolha depende da estratégia adotada pelos quatro vizinhos do sítio escolhido. | ||
* Ao escolher estar ou não em quarentena, esses componentes | * Ao escolher estar ou não em quarentena, esses componentes têm probabilidades diferentes de adquirir a doença (<math>\beta_Q</math> e <math>\beta_N</math>) e se tornar infectados. | ||
* Infectados possuem a mesma probabilidade de se tornarem recuperados. | * Infectados possuem a mesma probabilidade de se tornarem recuperados. | ||
* Após recuperados da doença, as pessoas não conseguem adquiri- | * Após recuperados da doença, as pessoas não conseguem adquiri-la novamente. | ||
* Todos os indivíduos escolhem estar ou não isolados | * Todos os indivíduos escolhem estar ou não isolados independente do seu estado de infecção, mas somente a quarentena dos suscetíveis afeta a evolução SIR. | ||
Para simular a quarentena voluntária é utilizado o jogo definido pelo [https://pt.wikipedia.org/wiki/Dilema_do_prisioneiro Dilema do Prisioneiro]. Esse dilema descreve a situação | Para simular a quarentena voluntária é utilizado o jogo definido pelo [https://pt.wikipedia.org/wiki/Dilema_do_prisioneiro Dilema do Prisioneiro]. Esse dilema descreve a situação em que dois condenados ('''A''' e '''B''') precisam decidir se cooperam ou não sem saber a decisão do seu par. Para isso temos quatro possibilidades: '''A''' e '''B''' cooperam (ambos saem com uma recompensa '''R'''), '''A''' coopera mas '''B''' não coopera ('''B''' ficaria com o valor da tentação '''T''' e '''A''' com o custo do sonso '''S'''), '''A''' não coopera e '''B''' coopera ('''A''' ficaria com o valor da tentação '''T''' e '''B''' com o custo do sonso '''S''') e a situação onde '''A''' e '''B''' não cooperam (ambos ganham com uma penalidade '''P'''). <ref name="hauert">HAUERT, Christoph; SZABÓ, György. ''Game theory and physics''. DOI: 10.1119/1.18485144 .</ref> | ||
Essas possibilidades podem ser resumidas em uma matriz de perdas e ganhos (''matriz de payoff''): | Essas possibilidades podem ser resumidas em uma matriz de perdas e ganhos (''matriz de payoff'' ou ''[https://pt.wikipedia.org/wiki/Dilema_do_prisioneiro forma normal]''): | ||
{| class="wikitable" | {| class="wikitable" style="margin-left:auto; margin-right:auto" | ||
|- | |- | ||
! scope="col"| | ! style="padding:10px" scope="col"| | ||
! scope="col" center| A coopera | ! style="padding:10px" scope="col" center| A coopera | ||
! scope="col"| A não coopera | ! style="padding:10px" scope="col"| A não coopera | ||
|- | |- | ||
! scope="row"| B coopera | ! style="padding:10px" scope="row"| B coopera | ||
| center | R / R | | style="padding:10px; text-align:center" | R / R | ||
| S / T | | style="padding:10px; text-align:center" | S / T | ||
|- | |- | ||
! scope="row"| B não coopera | ! scope="row"| B não coopera | ||
| T / S | | style="padding:10px; text-align:center" | T / S | ||
| P / P | | style="padding:10px; text-align:center" |P / P | ||
|} | |} | ||
Os valores da matriz ''payoff'' devem obedecer a ordem T > R > P > S. Além disso, para simulações com várias iterações deve ser obedecido que 2R > T + S. <ref name="hauert">HAUERT, Christoph; SZABÓ, György. ''Game theory and physics''. DOI: 10.1119/1.18485144 .</ref> | Os valores da matriz ''payoff'' devem obedecer a ordem <math>T > R > P > S</math>. Além disso, para simulações com várias iterações deve ser obedecido que <math>2R > T + S</math>. <ref name="hauert">HAUERT, Christoph; SZABÓ, György. ''Game theory and physics''. DOI: 10.1119/1.18485144 .</ref> | ||
A proposta de observar a evolução da infecção dependendo da quarentena precisa utilizar mais de um par de interagentes, por isso é definido uma rede onde cada componente | A proposta de observar a evolução da infecção dependendo da quarentena precisa utilizar mais de um par de interagentes, por isso é definido uma rede onde cada componente ocupa um espaço fixo sem poder se movimentar. A partir disso, cada um desses componentes interage com seus quatro vizinhos mais próximos (para os pontos do contorno é utilizado que as bordas são unidas por condições de contorno periódicas). <ref name="hauert">HAUERT, Christoph; SZABÓ, György. ''Game theory and physics''. DOI: 10.1119/1.18485144 .</ref> | ||
Segundo Hauert e Szabó <ref name="hauert">HAUERT, Christoph; SZABÓ, György. ''Game theory and physics''. DOI: 10.1119/1.18485144 .</ref>, os colaboradores tendem a ser extintos em jogos que consideram a interação aleatória, independente da sua concentração inicial, ou seja, todos tendem a não ganhar nada (não colaborar mutuamente) a fim de reduzir custos. Enquanto isso, se for proposto que um componente só escolhe uma estratégia conforme seus vizinhos, é visto | Segundo Hauert e Szabó <ref name="hauert">HAUERT, Christoph; SZABÓ, György. ''Game theory and physics''. DOI: 10.1119/1.18485144 .</ref>, os colaboradores tendem a ser extintos em jogos que consideram a interação aleatória, independente da sua concentração inicial, ou seja, todos tendem a não ganhar nada (não colaborar mutuamente) a fim de reduzir custos individuais. Enquanto isso, se for proposto que um componente só escolhe uma estratégia conforme seus vizinhos, é visto a formação de ''clusters'' de cooperadores e de não cooperadores; com isso, os componentes que estão na borda desses espaços, ganham na interação com os vizinhos colaboradores e perdem com a outra interação. | ||
A probabilidade de escolha pela troca (adquirir a mesma tática que o vizinho) é dada pela equação abaixo. As variáveis são: <math>P_{vizinho}</math> é a performance de um dos vizinhos do sítio (soma dos ganhos e perdas pela matriz ''payoff''), <math>S_{sitio}</math> é a performance do sítio, calculada pela interação entre os seus vizinhos da mesma forma que <math>P_{vizinho}</math> e <math>k</math> é a irracionalidade dos componentes. <ref name="hauert">HAUERT, Christoph; SZABÓ, György. ''Game theory and physics''. DOI: 10.1119/1.18485144 .</ref>. Dado um número aleatório entre <math>0</math> e <math>1</math>, se este for menor que a probabilidade <math>\phi_S</math> o sítio adota a estratégia do vizinho escolhido anteriormente. Assim, quando a probabilidade calculada for igual a 1, qualquer número escolhido resultará na mudança da estratégia. | |||
<math>\phi_S = [1 + \exp(-(P_{vizinho} - P_{sitio})/k)]^{-1}</math> | |||
Esse jogo de quarentena é acoplado ao sistema SIR anteriormente descrito. A única diferença para o SIR sem o jogo é que as probabilidades de um componente S se tornar infectado mudam a partir do seu estado de quarentena. | |||
Esse jogo de quarentena é acoplado ao sistema SIR anteriormente descrito. A única diferença para o SIR sem o jogo é que as probabilidades de um componente <math>S</math> se tornar infectado mudam a partir do seu estado de quarentena. | |||
== Implementação == | == Implementação == | ||
Os códigos da simulação foram implementados na linguagem [https://en.wikipedia.org/wiki/C_(programming_language) C], para a visualização foi utilizada a linguagem [https://pt.wikipedia.org/wiki/Python Python]. Ambos ''scripts'' estão disponíveis no [https://replit.com/@JuliaRemus/sirmodificado#README.md projeto criado no Replit] | Os códigos da simulação foram implementados na linguagem [https://en.wikipedia.org/wiki/C_(programming_language) C], para a visualização foi utilizada a linguagem [https://pt.wikipedia.org/wiki/Python Python]. Ambos ''scripts'' estão disponíveis no [https://replit.com/@JuliaRemus/sirmodificado#README.md projeto criado no Replit]. | ||
=== Implementação modelo SIR === | === Implementação modelo SIR === | ||
Código fonte do modelo SIR: [[Código Modelo Sir]] | |||
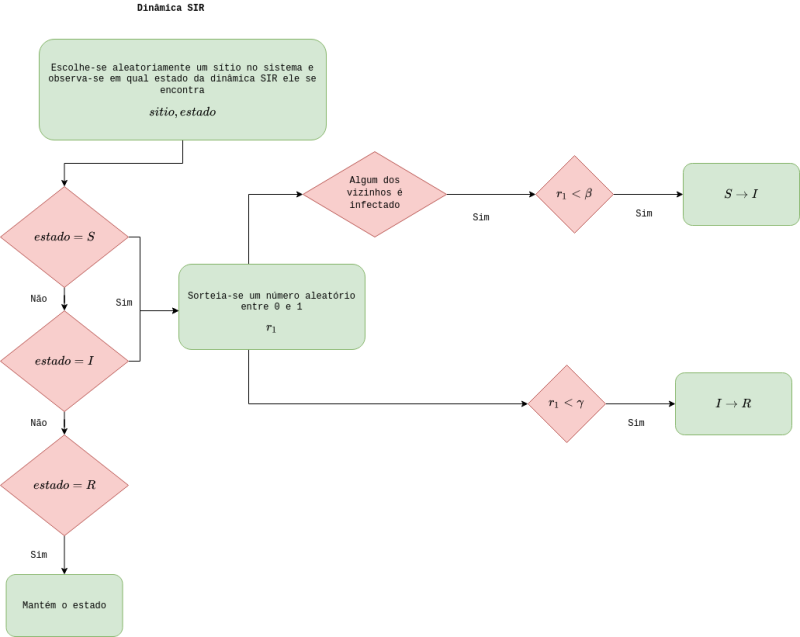
O fluxograma abaixo descreve a implementação computacional deste modelo: | |||
[[Arquivo:fluxograma_sir_certo.png|center|thumb|800px|Fluxograma para a dinâmica SIR]] | |||
=== Implementação modelo SIR com quarentena voluntária === | === Implementação modelo SIR com quarentena voluntária === | ||
Algumas modificações são realizadas | Algumas modificações são realizadas a partir do código anterior para adicionar a quarentena voluntária: a probabilidade do indivíduo passar de suscetível a infectado depende da escolha pela quarentena e é adicionada a escolha de se isolar ou não. | ||
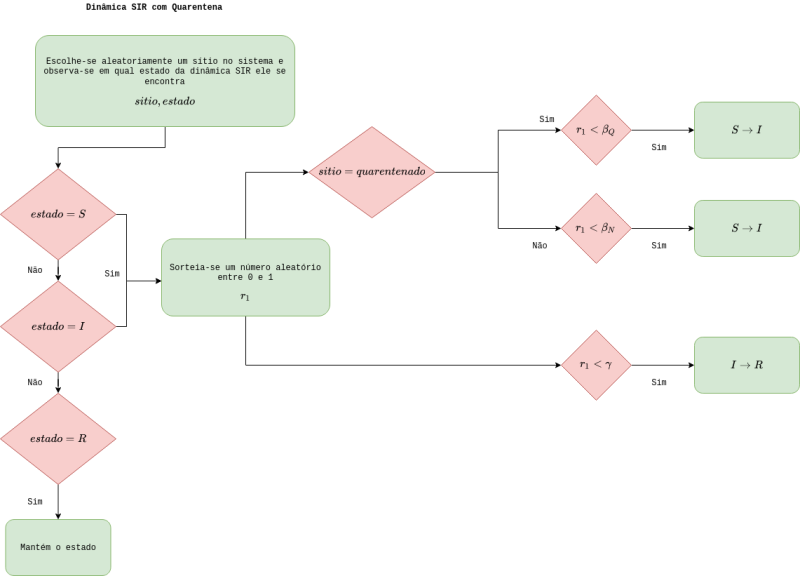
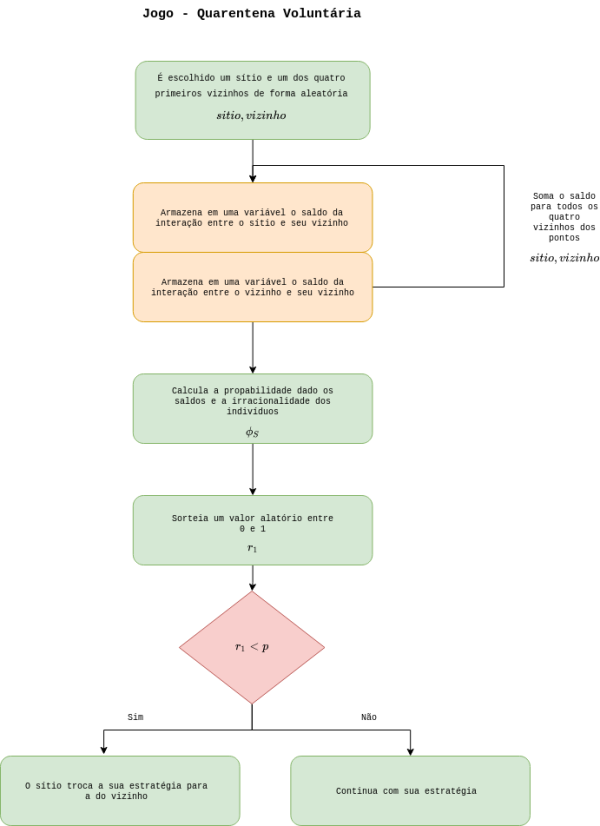
A estrutura principal do código é dada pelo laço temporal onde a cada tempo é chamado o modelo SIR e o jogo da quarentena. Antes de entrar no ''loop'' é realizada a inicialização do sistema definindo o estado SIR e de quarentena dos indivíduos em vetores distintos e a matriz ''payoff'' do jogo. A seguir é possível visualizar o fluxograma para as funções da evolução do SIR e do jogo da quarentena. | |||
Os códigos estão disponíveis No [https://replit.com/@JuliaRemus/sirmodificado#README.md projeto criado no Replit], os arquivos utilizados foram ''versao_viz_quarentena.c'' para a dinâmica SIR com quarentena voluntária e ''mc.h'' para o suporte com os números aleatórios. O primeiro código gerará três arquivos de saída: ''outup.txt'', contendo a evolução temporal do SIR, ''output_dinamica_sir.txt'', com o vetor de indivíduos contendo o estado SIR de cada um, sendo que cada linha corresponde a um tempo e ''output_dinamica_loc.txt'', com o vetor de indivíduos contendo o estado de quarentena de cada um, sendo que cada linha corresponde a um tempo. Para realizar a visualização, é utilizado o arquivo ''visualizacao.py'' que lê os arquivos gerados e faz os gráficos buscados (note, que está separado em blocos por ''#%%'', sendo possível utilizar apenas alguns softwares como ''Spyder'' ou ''Visual Studio''); alguns comandos para geração das animações no ''gnuplot'' estão comentados ao longo do código e podem ser usados. | |||
[[Arquivo:fluxograma_sir_quarentena_certo_2.png|center|thumb|800px|Fluxograma para a dinâmica SIR com quarentena]] | |||
[[Arquivo:diagrama_jogo_certo.png|thumb|center|600px|Fluxograma para a quarentena voluntária]] | |||
== Resultados e Discussão == | == Resultados e Discussão == | ||
=== Resultados SIR === | |||
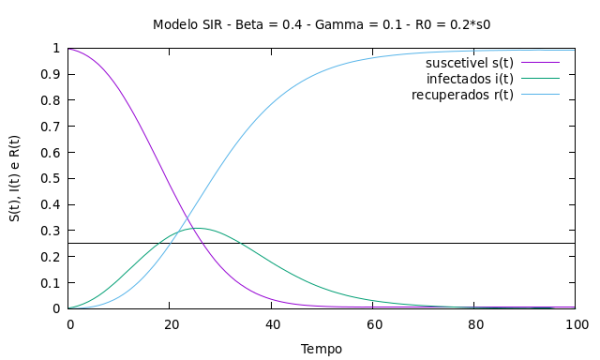
Abaixo segue o primeiro gráfico obtido para a dinâmica do modelo SIR, o qual mostra a fração do número de indivíduos suscetíveis, infectados, e recuperados com relação ao tempo. Este sistema contém uma população constante de <math> N = 10^6 </math>, taxa de transmissibilidade <math> \beta = 0.4 </math>, taxa de remoção da doença <math> \gamma = 0.1 </math>. Inicialmente o número de indivíduos suscetíveis corresponde a 98,98% do sistema, enquanto 0,02% dos indivíduos são infectados. Observa-se que a fração de indivíduos infectados aumenta a medida que o tempo avança, porém quando o número de indivíduos suscetíveis atinge a fração <math>\gamma / \beta = 0.25</math> (representada pela reta horizontal) a fração de indivíduos infectados atinge o ponto máximo e posteriormente entra em declínio. Podemos observar, utilizando a expressão (8), que valores acima da fração <math>\gamma / \beta = 0.25</math> correspondem ao número de reprodução <math> R_0 > 1</math>, enquanto valores abaixo da fração <math>\gamma / \beta = 0.25</math> correspondem ao número de reprodução <math> R_0 < 1</math>. | |||
[[Arquivo:figura_sir_01.png|center|thumb|600px|Modelo SIR - População total N =1000^2]] | |||
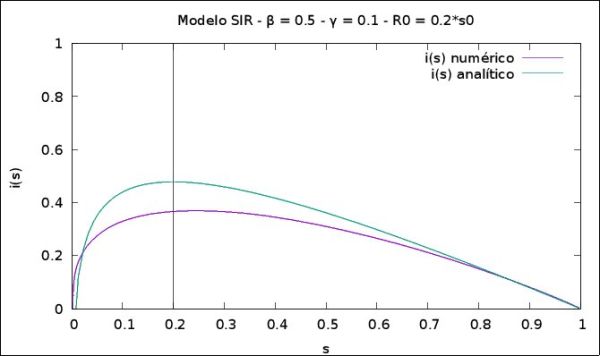
Obtemos a curva numérica do número de indivíduos infectados pelo número de indivíduos suscetíveis <math> i(s) </math>, comparamos esta solução com a solução analítica expressa por (9). Note que a solução numérica se aproxima da analítica na situação inicial, pois o efeito dos vizinhos neste intervalo é mínimo, já que a maioria dos indivíduos é suscetível. No entanto, a medida que a pandemia avança, o efeito dos vizinhos torna-se relevante, e como a expressão analítica não contempla este efeito, as duas curvas diferenciam-se uma da outra. Podemos observar que quando <math> s < \gamma/\beta </math> o número de indivíduos infectados aumenta, já quando a fração de indivíduos se iguala a <math> \gamma/ \beta </math> o número de indivíduos infectados se torna máximo e a pandemia estabiliza, por fim quando <math> s > \gamma/ \beta </math> temos o declínio da pandemia. | |||
[[Arquivo:Imagem 02.jpg|center|thumb|600px|Modelo SIR - População total N =1000^2]] | |||
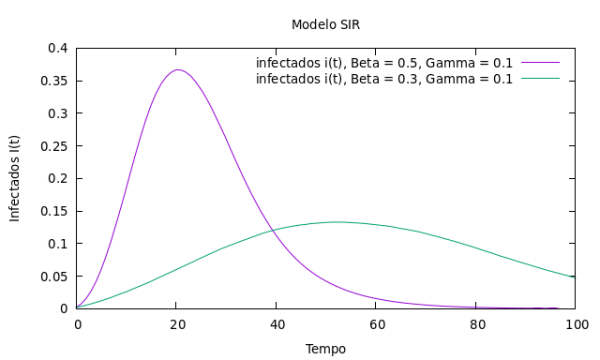
O gráfico abaixo tem a mesma configuração para ambas as curvas, mas parâmetros de taxa de transmissão <math> \beta </math> diferentes. Podemos observar, que para a curva com maior taxa de transmissão, o pico da fração de indivíduos infectados é bastante superior ao da outra. Podemos concluir, através deste gráfico, que medidas estratégicas para diminuir a taxa <math> \beta </math> são importantes para não congestionar o sistema de saúde. | |||
[[Arquivo:figura_sir_03.png|center|thumb|600px|Modelo SIR - População total N =1000^2]] | |||
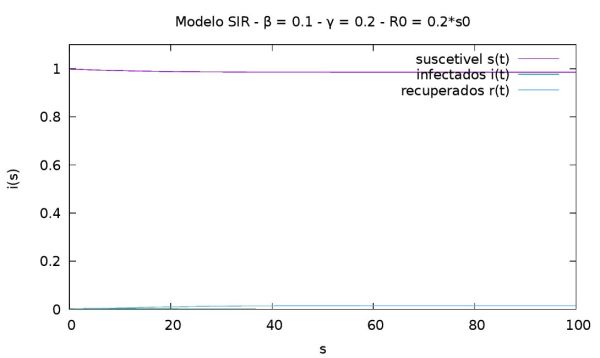
O gráfico abaixo apresenta uma população constante de <math> N = 10^6 </math>, taxa de transmissão <math> \beta = 0.1 </math> e taxa de remoção da doença <math> \gamma = 0.2 </math>. Portanto, temos um número de reprodução <math> R_0 </math> sempre menor do que um, isto implica que a pandemia nunca irá ocorrer, tal como vemos no gráfico abaixo. | |||
[[Arquivo:Figura sir 04.jpeg|center|thumb|600px|Modelo SIR - População total N =1000^2]] | |||
=== Resultados SIR com quarentena voluntária === | |||
Na simulação com quarentena voluntária é utilizado o SIR com a dinâmica dependendo dos vizinhos infectados. Para os gráficos abaixo mostrados foram utilizadas os seguintes parâmetros: | |||
{| class="wikitable" style="margin-left:auto; margin-right:auto" | |||
|- | |||
! scope="col" style="padding:10px" colspan="3" | Simulação | |||
! scope="col" style="padding:10px" colspan="3" | Dinâmica SIR | |||
! scope="col" style="padding:10px" colspan="5" | Matriz de ''Payoff'' | |||
|- | |||
|- | |||
| scope="col" style="padding:10px" center | Tempo (passos) | |||
| scope="col" style="padding:10px" center | Número de indivíduos | |||
| scope="col" style="padding:10px" center | Porcentagem de indivíduos suscetíveis | |||
| scope="col" style="padding:10px" center | <math>\beta_Q</math> | |||
| scope="col" style="padding:10px" center | <math>\beta_N</math> | |||
| scope="col" style="padding:10px" center | <math>\gamma</math> | |||
| scope="col" style="padding:10px" center | <math>T</math> | |||
| scope="col" style="padding:10px" center | <math>S</math> | |||
| scope="col" style="padding:10px" center | <math>R</math> | |||
| scope="col" style="padding:10px" center | <math>P</math> | |||
| scope="col" style="padding:10px" center | <math>k</math> | |||
|- | |||
| style="padding:10px" | 500 | |||
| style="padding:10px" | 3600 | |||
| style="padding:10px" | 99,9% <math>S</math> | |||
| style="padding:10px" | 0.0 | |||
| style="padding:10px" | 0.25 | |||
| style="padding:10px" | 0.08 | |||
| style="padding:10px" | 1.01 | |||
| style="padding:10px" | 0.0 | |||
| style="padding:10px" | 1.0 | |||
| style="padding:10px" | 0.005 | |||
| style="padding:10px" | 0.1 | |||
|} | |||
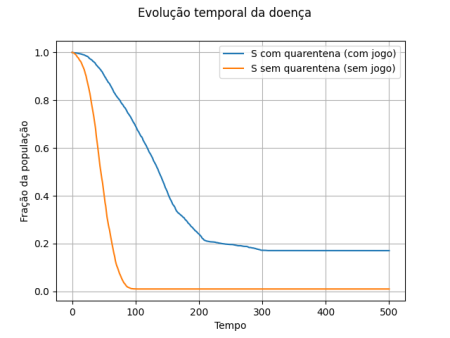
É utilizado que os indivíduos em isolamento estão distribuídos aleatoriamente; inicialmente é proposto uma relação de 1:1 de estados de quarentena. A dinâmica SIR sem o jogo é realizada definindo que nenhuma pessoa está isolada. Com essas premissas e com os parâmetros os resultados obtidos são apresentados a seguir, neles é possível comparar a simulação com a escolha da quarentena e sem. Define-se que o indivíduo isolado não tem chance de se tronar infectado (<math>\beta_Q = 0</math>), o que não é totalmente verdade, pois existe sempre algum contato das pessoas mesmo que ínfimo. | |||
<div><ul> | |||
<li style="display: inline-block; vertical-align: top;"> [[Arquivo:comparacao_comsem_quarentena_inicial.png|thumb|450px|center|Comparação da evolução entre os suscetíveis na dinâmica SIR e com parte da população quarentenada]] </li> | |||
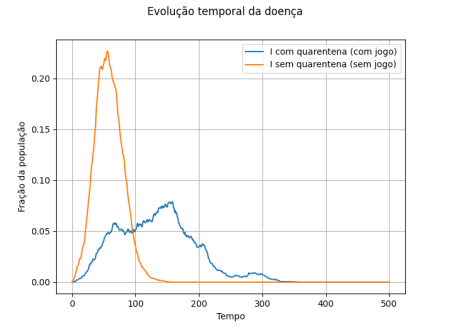
<li style="display: inline-block; vertical-align: top;"> [[Arquivo:comparacao_comsem_quarentena_inicial_infectados.png|thumb|450px|center|Comparação da evolução entre os infectados na dinâmica SIR e com parte da população quarentenada]] </li> | |||
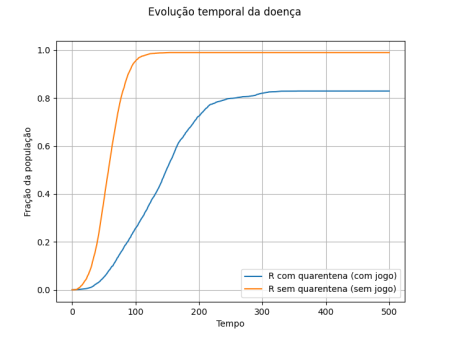
<li style="display: inline-block; vertical-align: top;"> [[Arquivo:comparacao_comsem_quarentena_inicial_recuperados.png|thumb|450px|center|Comparação da evolução entre os recuperados na dinâmica SIR e com parte da população quarentenada]] </li> | |||
</ul></div> | |||
<div><ul> | |||
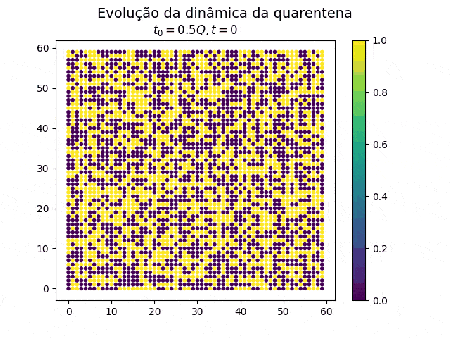
<li style="display: inline-block; vertical-align: top;"> [[Arquivo:gif_loc_50_dez.gif|thumb|450px|center|Evolução do sistema SIR a partir de 50% dos componentes isolados]] </li> | |||
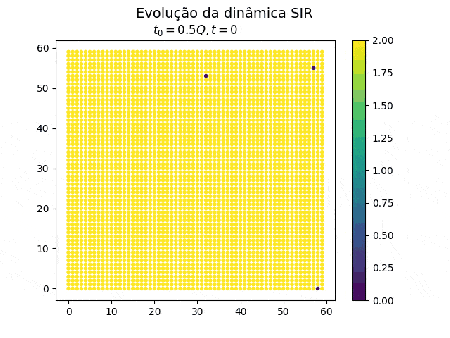
<li style="display: inline-block; vertical-align: top;"> [[Arquivo:gif_sir_50_dez.gif|thumb|450px|center|Evolução do sistema SIR a partir de 50% dos componentes isolados]] </li> | |||
</ul></div> | |||
Com os parâmetros utilizados, percebe-se que a quarentena auxilia na diminuição de casos iniciais, diminuindo e distribuindo a onda de infectados ao longo do tempo (note que o tempo é em passos). Nos gráficos é mantida as relações apresentadas acima para o dilema do prisioneiro e também é definido <math>R_0 > 1</math>. | |||
Como é utilizado que os indivíduos em quarentena não posuem nenhuma chance de se infectar e é necessário um vizinho infectado para passar a doença adiante, nota-se a formação de ilhas de suscetíveis na animação à direita. | |||
Ainda não é percebido a onda após a primeira bem definida como no artigo de referência, ficam somente oscilações ao longo do tempo. Com a modificação dos parâmetros da dinâmica SIR e da escolha da quarentena percebe-se que a variação mínima deles (por exemplo um décimo na probabilidade de um não quarentenado contrair a doença) faz com que a evolução da doença ocorra de forma totalmente diferente, muitas vezes tendendo a parecer a evolução SIR sem o jogo. | |||
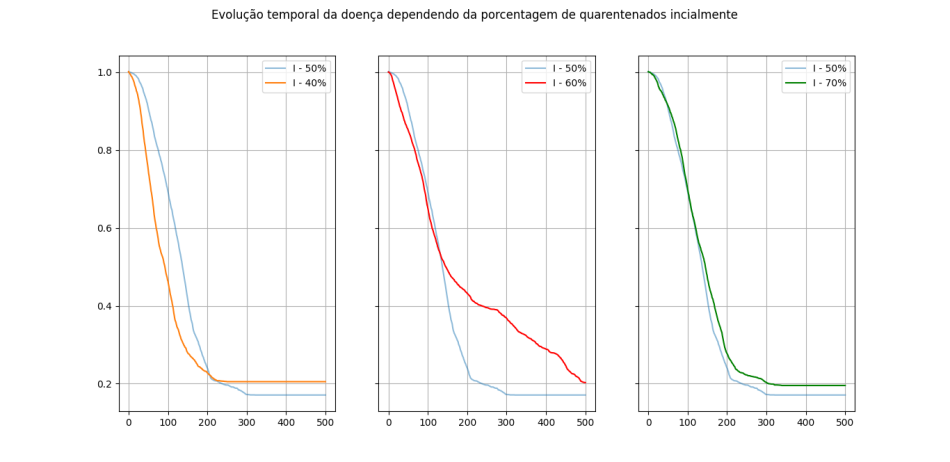
Por esse motivo, foi modificada a percentagem inicial de indivíduos em quarentena - mantendo os outros parâmetros - para avaliar como essa variável agia no sistema. Pelo gráfico abaixo é possível notar que acima de <math>50 \%</math> de indivíduos fora da quarentena a evolução tende ao SIR sem jogo, mas que abaixo desse valor é possível ver a formação de ondas menores. | |||
[[Arquivo:comparacao_quarentenados_inicial.png|thumb|950px|center|Comparação da evolução dos indivíduos suscetíveis variando a porcentagem inicial de pessoas em quarentena]] | |||
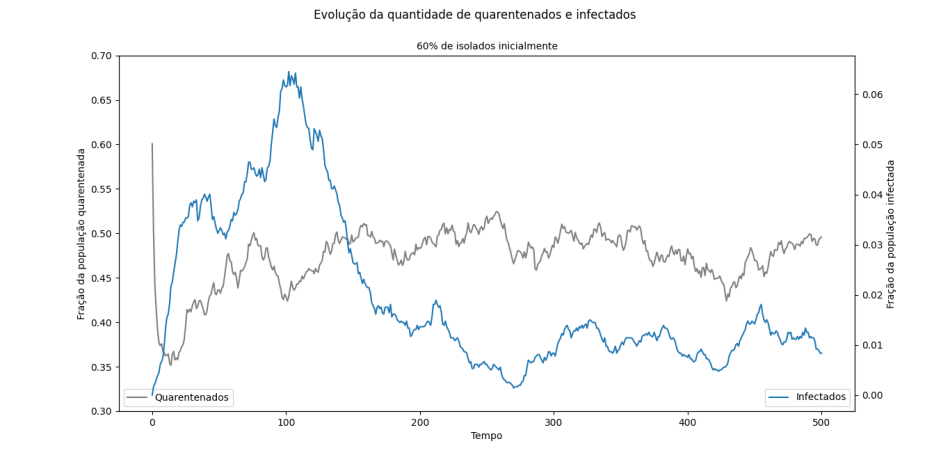
Mesmo os valores abaixo possuírem essa evolução tipo degrau mais acentuada para os suscetíveis, a relação entre indivíduos infectados e em quarentena não é conclusiva, como pode ser visto no gráfico que mostra a evolução das duas variáveis. | |||
[[Arquivo:evolucao_infectados_quarentenados.png|thumb|950px|center|Evolução da população infectada e em quarentena para 60% dos indivíduos inicialmente isolados]] | |||
Os resultados obtidos mostram que a quarentena voluntária diminui significativamente o número de infectados | Os resultados obtidos mostram que a quarentena voluntária diminui significativamente o número de infectados na '''primeira onda''', tendência prevista por outras pesquisas e que evita o esgotamento dos serviços de saúde. <ref>MAGENTA, Matheus. Quarentenas funcionam para combater o coronavírus? Veja o que dizem os estudos. BBC News. Disponível em: <https://www.bbc.com/portuguese/internacional-52830618></ref> | ||
Outro comportamento observado nos dados da Covid-19, foi o aparecimento de ondas de contaminação, isto é, uma sucessão de aumentos e diminuições na | Outro comportamento observado nos dados da Covid-19, foi o aparecimento de ondas de contaminação, isto é, uma sucessão de aumentos e diminuições na quantidade de infectados. Foi observado que tanto os parâmetros da matriz de ''payoff'' e os da dinâmica SIR quanto o sistema inicial da quarentena, interferem na evolução da doença de maneiras diferentes, expressando tanto comportamentos ondulatórios quanto similares ao SIR normal. Diferentemente do observado pelo método do campo médio, o comportamento ondulatório foi mais sutil, não sabemos se o problema foram os parâmetros utilizados ou se o projeto realmente não consegue simular o problema real. | ||
== Próximos Passos == | |||
Algumas pendências são deixadas para um futuro trabalho: | |||
* Automatizar os testes com parâmetros | |||
* Estudar melhor a relação entre parâmetros (SIR e quarentena) e a quantidade inicial de indivíduos isolados | |||
* Buscar se há diferenças quando a percepção do componente está só no primeiro vizinho e quando ele consegue ver mais o sistema | |||
* Desenvolver um jogo onde a escolha pela quarentena seja dada pelo estado infectado ou não do vizinho, não pela sua quarentena | |||
== Referências == | == Referências == | ||
<references /> | <references /> | ||
Edição atual tal como às 13h15min de 30 de dezembro de 2021
Grupo: Gabriel Schmökel, Julia Remus e Luis Gustavo Lang Gaiato
O objetivo do trabalho é realizar a implementação do modelo SIR (Suscetível, Infectado e Recuperado) e de um modelo simplificado do proposto pelo artigo "An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics" [1] utilizando Monte Carlo. Espera-se obter ondas de infecção quando utilizado o processo de quarentena voluntária, tal qual observada pelos dados da Covid-19 e encontrada pelo artigo de referência do modelo.
Será apresentada uma breve introdução sobre o tema e as equações que envolvem o desenvolvimento dos cálculos, as implementações e seus respectivos resultados. São deixados alguns objetivos futuros para um trabalho posterior.
Introdução
A pandemia atual mostrou que táticas para mitigar o avanço da doença dependem não só de medidas governamentais, mas também da percepção do indivíduo nesse meio. [2]. Essa percepção depende da métrica utilizada por cada pessoa, levando em consideração fatores como: prejuízos psicológicos, situação econômica, o entendimento sobre o que é certo (como a sociedade o enxerga, quais as verdades que são consideradas pelo indivíduo), a escolha pelo bem comum, entre outros. A visão do indivíduo pode mudar ao longo do tempo e, com isso, modificar como a doença evolui - como é quantificado pela formação de ondas de infecção atualmente. [3]
A fim de simular esses cenários de pandemia com e sem a percepção do indivíduo, propõe-se um trabalho com o objetivo de realizar a implementação do modelo SIR e de um modelo simplificado do proposto pelo artigo "An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics" [1] utilizando Monte Carlo.
O modelo apresentado por Marco Amaral, et al [1] propõe que o indivíduo escolha adequar-se a uma das estratégias da quarentena (fazer ou não) dependendo do risco que observa a partir da quantidade de infectados no sistema. Acoplada à escolha da estratégia, está o modelo SIR com parâmetros distintos para indivíduos não isolados e isolados. Para a solução, os autores utilizam a teoria de campo médio, obtendo ondas de infecção ao longo do tempo.
Neste trabalho, a escolha da estratégia pelo indivíduo se dará de acordo com o estado dos seus vizinhos mais próximos - utilizado o dilema do prisioneiro - enquanto a evolução dos infectados no sistema será realizada com o modelo SIR, assim como no trabalho citado. Para a simulação foi utilizado o método de Monte Carlo.
É esperado obter as ondas de infecção como previsto por Marco Amaral, et al [1] e observadas nos dados reais da Covid-19, ambos os exemplos podem ser observados a seguir. Como o método é diferente, não é esperado que as ondas sejam iguais às do artigo, mas sim, um movimento mais sutil.
-
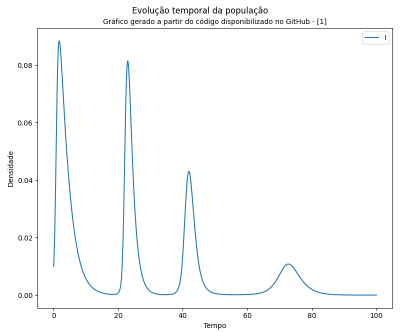 Resultado do modelo proposto por Marco Amaral, et al [1]
Resultado do modelo proposto por Marco Amaral, et al [1]
No gráfico da direita pode-se observar a quantidade de casos diários (infectados) na Alemanha e no Reino Unido ao longo do tempo, vê-se que existem ondas de infecção. Já no gráfico da direita, é possível observar a solução obtida por Marco Amaral, et al [1].
O esquemático do modelo SIR com a escolha da quarentena pode ser visto na seção Modelo SIR com quarentena voluntária.
Modelos
Modelo SIR
Em 1927 Kermack e McKendrick elaboraram o modelo SIR que tinha como função descrever o comportamento de uma pandemia [4]. O modelo SIR é um dos mais simples modelos comportamentais, o qual descreve a variação de três parâmetros ao longo do tempo:
- Suscetível (S): Número de indivíduos suscetíveis. Quando um indivíduo suscetível e um infectado entram em contato, o indivíduo suscetível tem uma probabilidade de contrair a doença, caso contraia o indivíduo deixa de ser suscetível e torna-se infectado.
- Infectado (I): Número de indivíduos infectados. Indivíduos infectados tem uma probabilidade de infectar indivíduos suscetíveis quando em contato, e uma probabilidade de tornar-se indivíduos removidos a medida que tempo avança.
- Recuperado ou Removido (R): Número de indivíduos removidos (recuperados ou mortos pela doença). Indivíduos que foram infectados, tornam-se recuperados ou mortos pela doença, desta forma entram na classificação de indivíduos removidos, já que não são mais suscetíveis a pegar a doença, pois adquiriram imunidade. Assumindo que o número de mortos é irrelevante ao se comparar com a população total, então o parâmetro recebe o nome de indivíduos recuperados ou resistentes.
A dinâmica de uma epidemia geralmente é mais rápida do que os números de nascimentos e óbitos, por essa razão se omite estas quantidades no modelo comportamental simples do SIR. Usando uma população fixa, Kermack e McKendrick chegaram nas seguintes equações diferenciais que descrevem a dinâmica de uma epidemia [4]:
O sistema descrito pelas equações acima é não linear, porém é possível derivar uma solução analítica de forma implícita [5].
A população total no SIR é constante, e pode ser expressada pela soma total dos indivíduos suscetíveis, infectados e removidos:
Na forma normalizada a expressão (4) é representada por:
A taxa de transmissão da doença é dada pela variável , esta depende de outras duas variáveis, a primeira indica a "transmissibilidade", definida por , a segunda indica o "número médio de contatos" entre infectados e suscetíveis, indicada por . Portanto, pode-se escrever a taxa de transmissão pela expressão:
A taxa de remoção da doença, indicada por , é o inverso do período infeccioso, indicada por , que o indivíduo permanecerá doente. Note, que quanto maior o período infeccioso, mais demorada é a remoção de Infectados para Removidos.
Dinâmica do Modelo SIR e o Número de Reprodução
O número básico de reprodução, , corresponde ao número médio de pessoas que serão contaminadas pela doença quando um indivíduo infectado é introduzido em uma população completamente suscetível [6].
Conforme o valor de temos o seguinte comportamento [6]:
- epidemia crescente;
- equilíbrio endêmico;
- epidemia decrescente.
Pode-se interpretar melhor o comportamento do número de reprodução analisando a curva . Para obter essa função dividimos a expressão (2) pela expressão (1) na forma normalizada, posteriormente integramos ambos os lados da igualdade, assim chegamos em [7]:
Derivando a expressão (9) em relação a observa-se que a função atinge o ponto de máximo quando . Nas situações em que temos e , obtemos respectivamente o comportamento crescente e decrescente para função . Na sequência é plotada a curva , observe que o sentido da abscissa é negativo para o avanço da pandemia.
Quando esta à direita da reta a epidemia irá aumentar o seu número de infectados, pois é maior do que . O número de infectados irá aumentar até o número de indivíduos suscetíveis ser igual a , posteriormente o número de infectados irá decair, pois é menor do que . Podemos entender melhor esta informação plotando as curvas i(s) e juntas:
Modelo SIR com quarentena voluntária
No esquemático pode-se ver o modelo utilizado no trabalho, ele é uma simplificação do artigo escrito por Amaral, et al [1]. Nele temos:
- Componentes suscetíveis podem estar ou não em quarentena. A probabilidade para a escolha depende da estratégia adotada pelos quatro vizinhos do sítio escolhido.
- Ao escolher estar ou não em quarentena, esses componentes têm probabilidades diferentes de adquirir a doença ( e ) e se tornar infectados.
- Infectados possuem a mesma probabilidade de se tornarem recuperados.
- Após recuperados da doença, as pessoas não conseguem adquiri-la novamente.
- Todos os indivíduos escolhem estar ou não isolados independente do seu estado de infecção, mas somente a quarentena dos suscetíveis afeta a evolução SIR.
Para simular a quarentena voluntária é utilizado o jogo definido pelo Dilema do Prisioneiro. Esse dilema descreve a situação em que dois condenados (A e B) precisam decidir se cooperam ou não sem saber a decisão do seu par. Para isso temos quatro possibilidades: A e B cooperam (ambos saem com uma recompensa R), A coopera mas B não coopera (B ficaria com o valor da tentação T e A com o custo do sonso S), A não coopera e B coopera (A ficaria com o valor da tentação T e B com o custo do sonso S) e a situação onde A e B não cooperam (ambos ganham com uma penalidade P). [8]
Essas possibilidades podem ser resumidas em uma matriz de perdas e ganhos (matriz de payoff ou forma normal):
| A coopera | A não coopera | |
|---|---|---|
| B coopera | R / R | S / T |
| B não coopera | T / S | P / P |
Os valores da matriz payoff devem obedecer a ordem . Além disso, para simulações com várias iterações deve ser obedecido que . [8]
A proposta de observar a evolução da infecção dependendo da quarentena precisa utilizar mais de um par de interagentes, por isso é definido uma rede onde cada componente ocupa um espaço fixo sem poder se movimentar. A partir disso, cada um desses componentes interage com seus quatro vizinhos mais próximos (para os pontos do contorno é utilizado que as bordas são unidas por condições de contorno periódicas). [8]
Segundo Hauert e Szabó [8], os colaboradores tendem a ser extintos em jogos que consideram a interação aleatória, independente da sua concentração inicial, ou seja, todos tendem a não ganhar nada (não colaborar mutuamente) a fim de reduzir custos individuais. Enquanto isso, se for proposto que um componente só escolhe uma estratégia conforme seus vizinhos, é visto a formação de clusters de cooperadores e de não cooperadores; com isso, os componentes que estão na borda desses espaços, ganham na interação com os vizinhos colaboradores e perdem com a outra interação.
A probabilidade de escolha pela troca (adquirir a mesma tática que o vizinho) é dada pela equação abaixo. As variáveis são: é a performance de um dos vizinhos do sítio (soma dos ganhos e perdas pela matriz payoff), é a performance do sítio, calculada pela interação entre os seus vizinhos da mesma forma que e é a irracionalidade dos componentes. [8]. Dado um número aleatório entre e , se este for menor que a probabilidade o sítio adota a estratégia do vizinho escolhido anteriormente. Assim, quando a probabilidade calculada for igual a 1, qualquer número escolhido resultará na mudança da estratégia.
Esse jogo de quarentena é acoplado ao sistema SIR anteriormente descrito. A única diferença para o SIR sem o jogo é que as probabilidades de um componente se tornar infectado mudam a partir do seu estado de quarentena.
Implementação
Os códigos da simulação foram implementados na linguagem C, para a visualização foi utilizada a linguagem Python. Ambos scripts estão disponíveis no projeto criado no Replit.
Implementação modelo SIR
Código fonte do modelo SIR: Código Modelo Sir
O fluxograma abaixo descreve a implementação computacional deste modelo:
Implementação modelo SIR com quarentena voluntária
Algumas modificações são realizadas a partir do código anterior para adicionar a quarentena voluntária: a probabilidade do indivíduo passar de suscetível a infectado depende da escolha pela quarentena e é adicionada a escolha de se isolar ou não.
A estrutura principal do código é dada pelo laço temporal onde a cada tempo é chamado o modelo SIR e o jogo da quarentena. Antes de entrar no loop é realizada a inicialização do sistema definindo o estado SIR e de quarentena dos indivíduos em vetores distintos e a matriz payoff do jogo. A seguir é possível visualizar o fluxograma para as funções da evolução do SIR e do jogo da quarentena.
Os códigos estão disponíveis No projeto criado no Replit, os arquivos utilizados foram versao_viz_quarentena.c para a dinâmica SIR com quarentena voluntária e mc.h para o suporte com os números aleatórios. O primeiro código gerará três arquivos de saída: outup.txt, contendo a evolução temporal do SIR, output_dinamica_sir.txt, com o vetor de indivíduos contendo o estado SIR de cada um, sendo que cada linha corresponde a um tempo e output_dinamica_loc.txt, com o vetor de indivíduos contendo o estado de quarentena de cada um, sendo que cada linha corresponde a um tempo. Para realizar a visualização, é utilizado o arquivo visualizacao.py que lê os arquivos gerados e faz os gráficos buscados (note, que está separado em blocos por #%%, sendo possível utilizar apenas alguns softwares como Spyder ou Visual Studio); alguns comandos para geração das animações no gnuplot estão comentados ao longo do código e podem ser usados.
Resultados e Discussão
Resultados SIR
Abaixo segue o primeiro gráfico obtido para a dinâmica do modelo SIR, o qual mostra a fração do número de indivíduos suscetíveis, infectados, e recuperados com relação ao tempo. Este sistema contém uma população constante de , taxa de transmissibilidade , taxa de remoção da doença . Inicialmente o número de indivíduos suscetíveis corresponde a 98,98% do sistema, enquanto 0,02% dos indivíduos são infectados. Observa-se que a fração de indivíduos infectados aumenta a medida que o tempo avança, porém quando o número de indivíduos suscetíveis atinge a fração (representada pela reta horizontal) a fração de indivíduos infectados atinge o ponto máximo e posteriormente entra em declínio. Podemos observar, utilizando a expressão (8), que valores acima da fração correspondem ao número de reprodução , enquanto valores abaixo da fração correspondem ao número de reprodução Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_0 < 1} .
Obtemos a curva numérica do número de indivíduos infectados pelo número de indivíduos suscetíveis Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle i(s) } , comparamos esta solução com a solução analítica expressa por (9). Note que a solução numérica se aproxima da analítica na situação inicial, pois o efeito dos vizinhos neste intervalo é mínimo, já que a maioria dos indivíduos é suscetível. No entanto, a medida que a pandemia avança, o efeito dos vizinhos torna-se relevante, e como a expressão analítica não contempla este efeito, as duas curvas diferenciam-se uma da outra. Podemos observar que quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s < \gamma/\beta } o número de indivíduos infectados aumenta, já quando a fração de indivíduos se iguala a Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma/ \beta } o número de indivíduos infectados se torna máximo e a pandemia estabiliza, por fim quando Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle s > \gamma/ \beta } temos o declínio da pandemia.
O gráfico abaixo tem a mesma configuração para ambas as curvas, mas parâmetros de taxa de transmissão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta } diferentes. Podemos observar, que para a curva com maior taxa de transmissão, o pico da fração de indivíduos infectados é bastante superior ao da outra. Podemos concluir, através deste gráfico, que medidas estratégicas para diminuir a taxa Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta } são importantes para não congestionar o sistema de saúde.
O gráfico abaixo apresenta uma população constante de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle N = 10^6 } , taxa de transmissão Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = 0.1 } e taxa de remoção da doença Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma = 0.2 } . Portanto, temos um número de reprodução Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_0 } sempre menor do que um, isto implica que a pandemia nunca irá ocorrer, tal como vemos no gráfico abaixo.
Resultados SIR com quarentena voluntária
Na simulação com quarentena voluntária é utilizado o SIR com a dinâmica dependendo dos vizinhos infectados. Para os gráficos abaixo mostrados foram utilizadas os seguintes parâmetros:
| Simulação | Dinâmica SIR | Matriz de Payoff | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Tempo (passos) | Número de indivíduos | Porcentagem de indivíduos suscetíveis | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_Q} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_N} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} | Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} |
| 500 | 3600 | 99,9% Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} | 0.0 | 0.25 | 0.08 | 1.01 | 0.0 | 1.0 | 0.005 | 0.1 |
É utilizado que os indivíduos em isolamento estão distribuídos aleatoriamente; inicialmente é proposto uma relação de 1:1 de estados de quarentena. A dinâmica SIR sem o jogo é realizada definindo que nenhuma pessoa está isolada. Com essas premissas e com os parâmetros os resultados obtidos são apresentados a seguir, neles é possível comparar a simulação com a escolha da quarentena e sem. Define-se que o indivíduo isolado não tem chance de se tronar infectado (Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_Q = 0} ), o que não é totalmente verdade, pois existe sempre algum contato das pessoas mesmo que ínfimo.
Com os parâmetros utilizados, percebe-se que a quarentena auxilia na diminuição de casos iniciais, diminuindo e distribuindo a onda de infectados ao longo do tempo (note que o tempo é em passos). Nos gráficos é mantida as relações apresentadas acima para o dilema do prisioneiro e também é definido Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_0 > 1}
.
Como é utilizado que os indivíduos em quarentena não posuem nenhuma chance de se infectar e é necessário um vizinho infectado para passar a doença adiante, nota-se a formação de ilhas de suscetíveis na animação à direita.
Ainda não é percebido a onda após a primeira bem definida como no artigo de referência, ficam somente oscilações ao longo do tempo. Com a modificação dos parâmetros da dinâmica SIR e da escolha da quarentena percebe-se que a variação mínima deles (por exemplo um décimo na probabilidade de um não quarentenado contrair a doença) faz com que a evolução da doença ocorra de forma totalmente diferente, muitas vezes tendendo a parecer a evolução SIR sem o jogo.
Por esse motivo, foi modificada a percentagem inicial de indivíduos em quarentena - mantendo os outros parâmetros - para avaliar como essa variável agia no sistema. Pelo gráfico abaixo é possível notar que acima de Falhou ao verificar gramática (MathML com retorno SVG ou PNG (recomendado para navegadores modernos e ferramentas de acessibilidade): Resposta inválida ("Math extension cannot connect to Restbase.") do servidor "https://wikimedia.org/api/rest_v1/":): {\displaystyle 50 \%} de indivíduos fora da quarentena a evolução tende ao SIR sem jogo, mas que abaixo desse valor é possível ver a formação de ondas menores.
Mesmo os valores abaixo possuírem essa evolução tipo degrau mais acentuada para os suscetíveis, a relação entre indivíduos infectados e em quarentena não é conclusiva, como pode ser visto no gráfico que mostra a evolução das duas variáveis.
Os resultados obtidos mostram que a quarentena voluntária diminui significativamente o número de infectados na primeira onda, tendência prevista por outras pesquisas e que evita o esgotamento dos serviços de saúde. [9]
Outro comportamento observado nos dados da Covid-19, foi o aparecimento de ondas de contaminação, isto é, uma sucessão de aumentos e diminuições na quantidade de infectados. Foi observado que tanto os parâmetros da matriz de payoff e os da dinâmica SIR quanto o sistema inicial da quarentena, interferem na evolução da doença de maneiras diferentes, expressando tanto comportamentos ondulatórios quanto similares ao SIR normal. Diferentemente do observado pelo método do campo médio, o comportamento ondulatório foi mais sutil, não sabemos se o problema foram os parâmetros utilizados ou se o projeto realmente não consegue simular o problema real.
Próximos Passos
Algumas pendências são deixadas para um futuro trabalho:
- Automatizar os testes com parâmetros
- Estudar melhor a relação entre parâmetros (SIR e quarentena) e a quantidade inicial de indivíduos isolados
- Buscar se há diferenças quando a percepção do componente está só no primeiro vizinho e quando ele consegue ver mais o sistema
- Desenvolver um jogo onde a escolha pela quarentena seja dada pelo estado infectado ou não do vizinho, não pela sua quarentena
Referências
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 1,6 AMARAL, Marco; OLIVEIRA, Marcelo de; JAVARONE, Marco, An epidemiological model with voluntary quarantine strategies governed by evolutionary game dynamics. arXiv:2008.05979v2 [physics.soc-ph] .
- ↑ SIEGRIST, Michael;BERTH, Angela. Worldviews, trust, and risk perceptions shape public acceptance of COVID-19 public health measures. DOI: https://doi.org/10.1073/pnas.2100411118.
- ↑ BAVEL, Jay; et al, Using social and behavioural science to support COVID-19 pandemic response. DOI: https://doi.org/10.1038/s41562-020-0884-z .
- ↑ 4,0 4,1 MCKENDRICK, A.G.; KERMACK, W. O.. Mathematical Theory of Epidemics. Disponível em: https://gallica.bnf.fr/ark:/12148/bpt6k56208r/f728.item.langFR
- ↑ Harko, Tiberiu; Lobo, Francisco S. N.; Mak, M. K. (2014). "Exact analytical solutions of the Susceptible-Infected-Recovered (SIR) epidemic model and of the SIR model with equal death and birth rates". Applied Mathematics and Computation. 236: 184–194. arXiv:1403.2160. Bibcode:2014arXiv1403.2160H. doi:10.1016/j.amc.2014.03.030. S2CID 14509477
- ↑ 6,0 6,1 M.G.Roberts. The pluses and minuses of r 0 . Journal of the Royal Society interface4, 2007.
- ↑ Beckley, Ross; Weatherspoon, Cametria; Alexander, Michael; Chandler, Marissa; Johnson, Anthony; Batt, Ghan S. (2013). Modeling epidemics with differential equations. Disponível em: http://www.tnstate.edu/mathematics/mathreu/filesreu/GroupProjectSIR.pdf
- ↑ 8,0 8,1 8,2 8,3 8,4 HAUERT, Christoph; SZABÓ, György. Game theory and physics. DOI: 10.1119/1.18485144 .
- ↑ MAGENTA, Matheus. Quarentenas funcionam para combater o coronavírus? Veja o que dizem os estudos. BBC News. Disponível em: <https://www.bbc.com/portuguese/internacional-52830618>





































![{\displaystyle \phi _{S}=[1+\exp(-(P_{vizinho}-P_{sitio})/k)]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4378c5a70eab56cc4c92bb08b7942aa4d330cd3b)